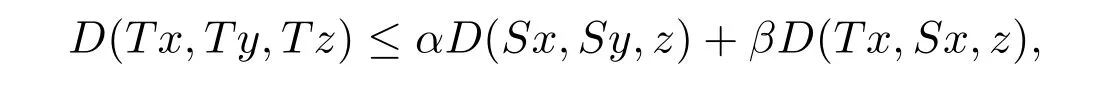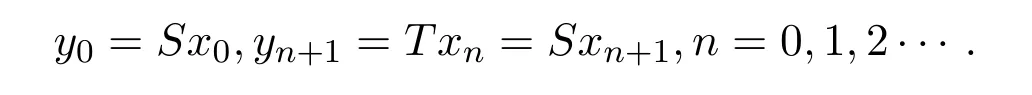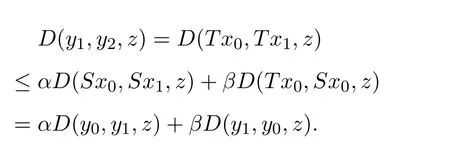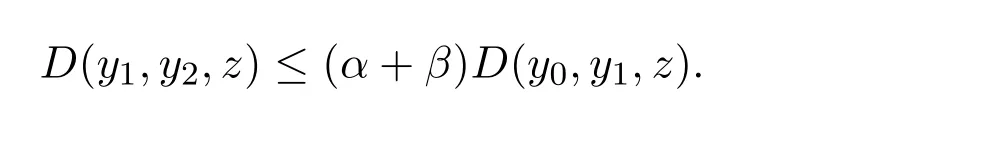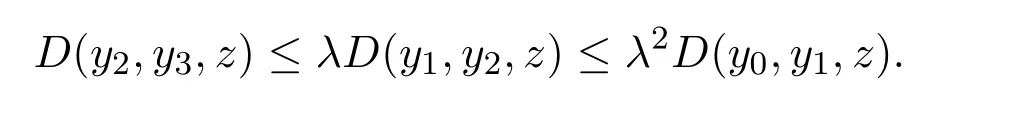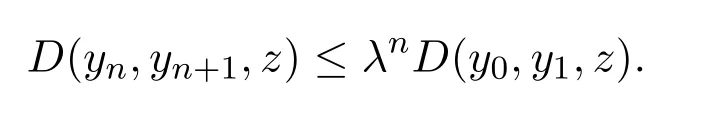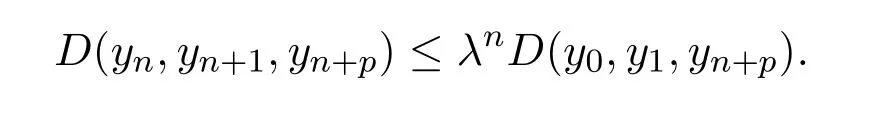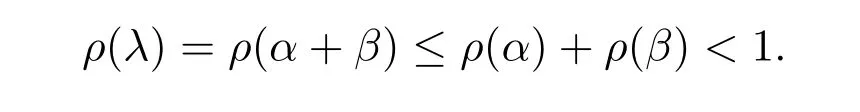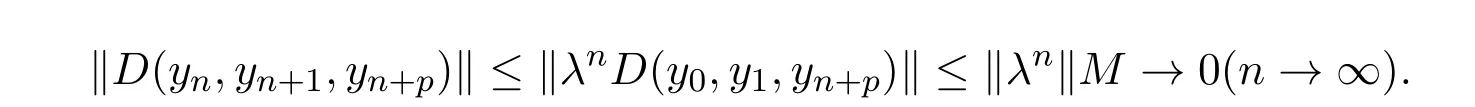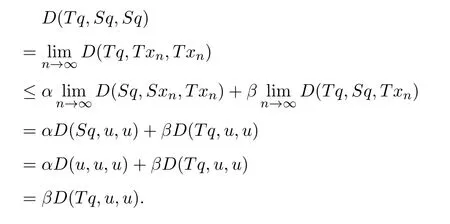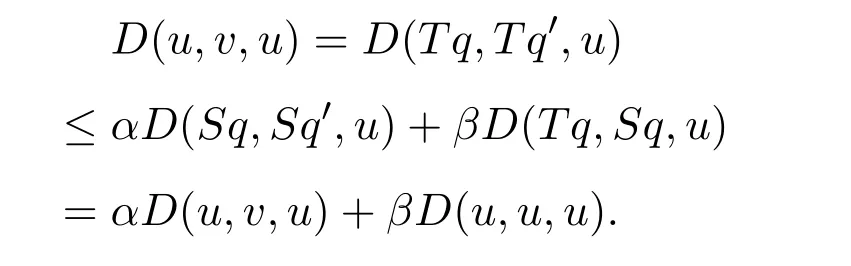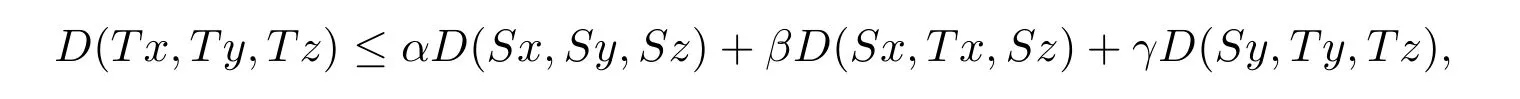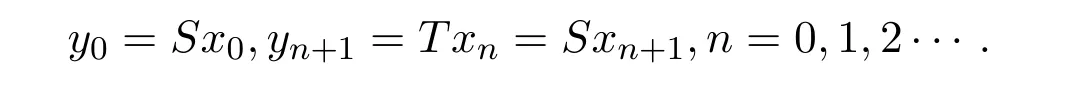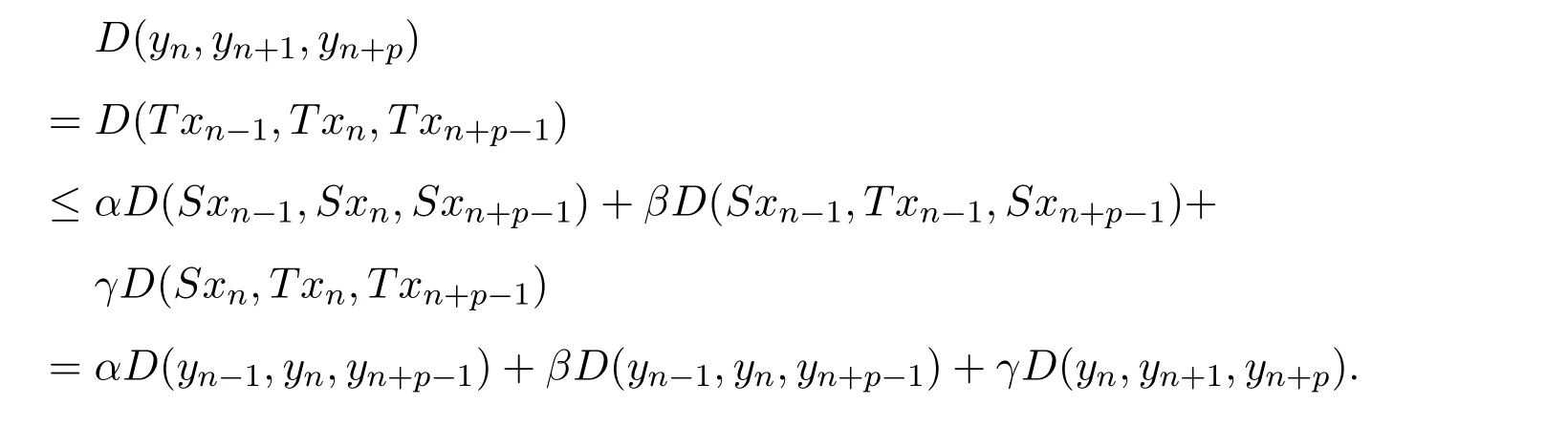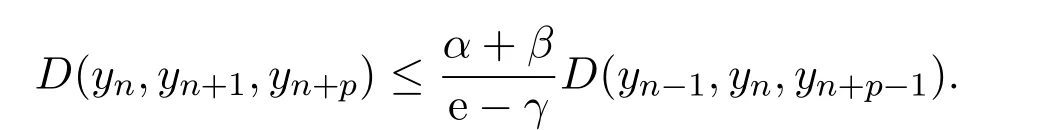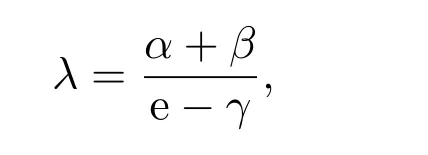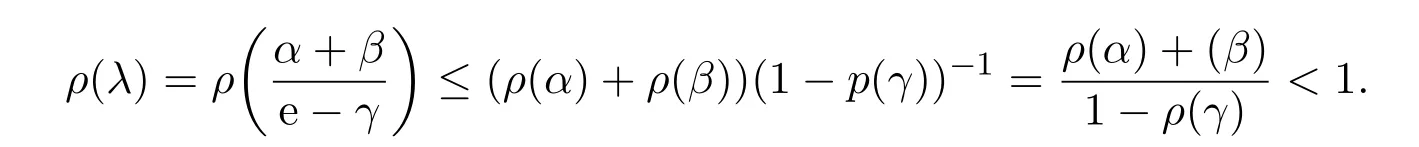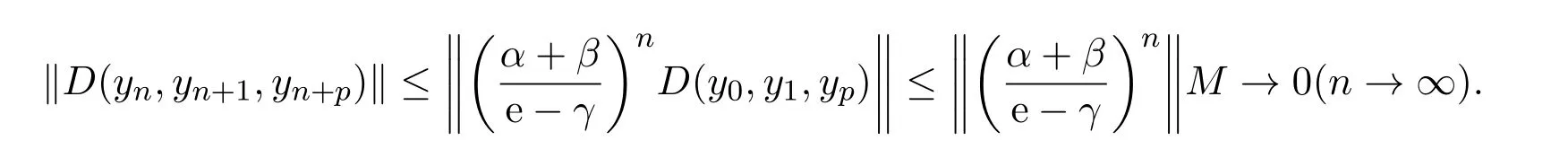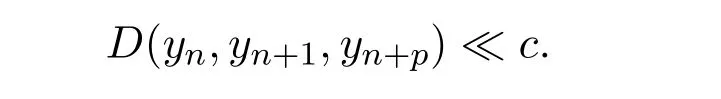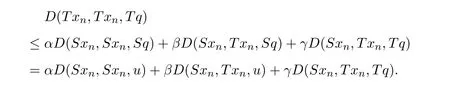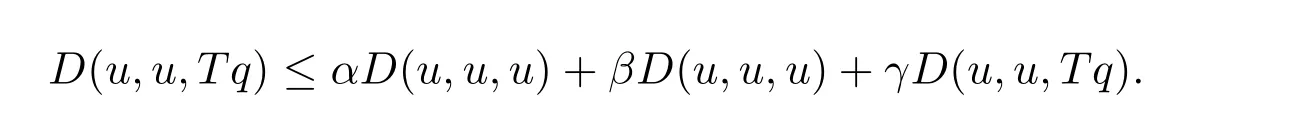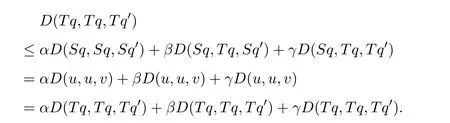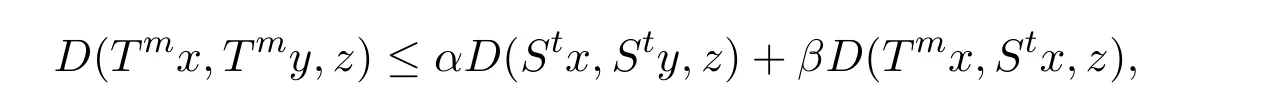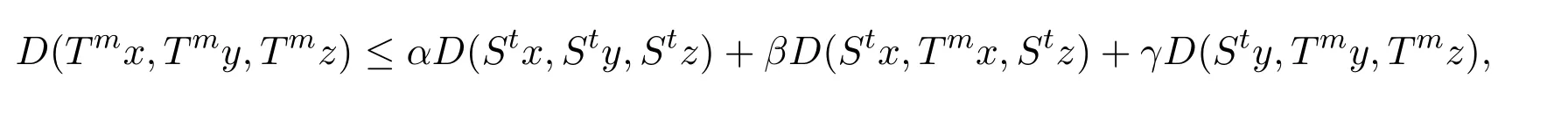具有Banach代數(shù)的錐D-度量空間和公共不動(dòng)點(diǎn)定理
張學(xué)智,薛西鋒
(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)
1 引言
1922年,Banach提出著名的壓縮映象原理[1].1992年,文獻(xiàn)[2]引入D-度量空間的定義,并在完備有界的D-度量空間中證得壓縮映射的不動(dòng)點(diǎn)定理.1996年,文獻(xiàn)[3-4]給出相容映象的定義,并證明了相容映象具有公共的不動(dòng)點(diǎn),此外也有大量作者對(duì)多個(gè)相容映象的公共不動(dòng)點(diǎn)問題作出研究[5-6].受Jungck的啟發(fā),文獻(xiàn)[7]在D-度量空間中引入相容映象的概念,并證明了D-度量空間中相容映象的公共不動(dòng)點(diǎn)定理.
2007年,文獻(xiàn)[8]用序Banach空間代替實(shí)數(shù),引入了錐度量空間,一些學(xué)者在此空間中得到了單個(gè)自映射的不動(dòng)點(diǎn)定理和多個(gè)相容映象的公共不動(dòng)點(diǎn)定理[9-10].2013年,文獻(xiàn)[11]用Banach代數(shù)代替序Banach空間得到具有Banach代數(shù)的錐度量空間,與度量空間相比較,其空間結(jié)構(gòu)發(fā)生了改變.近來,許多作者在刪去錐的正規(guī)性條件后,用不同的方法在不動(dòng)點(diǎn)理論方面作出新的研究.
基于以上內(nèi)容,本文將錐D-度量和Banach代數(shù)糅合在一起,得到具有Banach代數(shù)的錐D-度量空間的定義,并在刪去錐的正規(guī)性的條件下證得2個(gè)相容映象的公共不動(dòng)點(diǎn)定理,主要結(jié)果改進(jìn)了已有文獻(xiàn)的一些結(jié)論.
2 預(yù)備知識(shí)
設(shè)A為實(shí)的Banach代數(shù),即A是具有乘法運(yùn)算的實(shí)Banach空間,其運(yùn)算具備以下性質(zhì)(對(duì)任意的x,y,z∈A,α∈R,):(1)(xy)z=x(yz);(2)x(y+z)=xy+xz;(3)α(xy)=(αx)y=x(αy);(4).
本文總假設(shè)實(shí)Banach代數(shù)A具有單位元(即乘法單位元)e,滿足對(duì)任意x∈A均有ex=xe=x.一個(gè)元素x∈A稱為可逆的,如果存在一個(gè)元素(稱為它的一個(gè)逆元)y∈A使得xy=yx=e.x的逆元記作x?1.更詳細(xì)的內(nèi)容可以參照文獻(xiàn)[12].
下面是本文用到的一些重要的定義和引理.
引理2.1[12]設(shè)A是具有單位元 e的 Banach代數(shù),x∈A.若x的譜半徑ρ(x)<1,即.則e?x是可逆的,并且有.
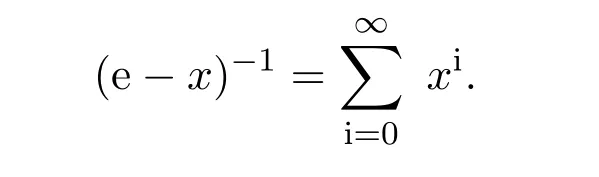
注記2.1[13]若ρ(x)<1,則∥xn∥→0(n→ ∞).
引理2.2[13]設(shè)A是具有單位元e的Banach代數(shù),x,y∈A.若x和y可交換,則有下列式子成立:
(1)ρ(xy)≤ρ(x)ρ(y);
(2)ρ(x+y)≤ρ(x)+ρ(y);
(3)|ρ(x)?ρ(y)|≤ρ(x?y).
引理2.3[13]設(shè)A是具有單位元e的Banach代數(shù),k∈A.若0≤ρ(k)<1,則
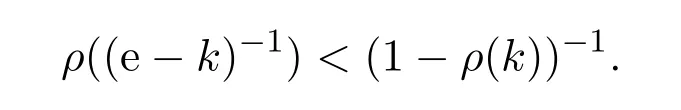
定義2.1[8]設(shè)A是具有單位元 e的 Banach代數(shù),A的一個(gè)非空閉凸子集P稱為錐,若 (1){θ,e}?P;(2)αP+βP?P對(duì)任意的非負(fù)實(shí)數(shù)α,β均成立;(3)P2=P·P?P;(4)P∩(?P)={θ}.其中θ為Banach代數(shù)A中的零元.對(duì)于A中的錐P,定義半序≤如下:x≤y當(dāng)且僅當(dāng)y?x∈P;x 下文假定P為Banach代數(shù)A中的體錐,≤是由在P中定義的半序,N是自然數(shù)集. 定義 2.2 設(shè)X是非空集合,若映射D:X×X×X×X?→A滿足: (1)θ≤D(x,y,z)對(duì)任意x,y,z,a∈X成立,D(x,y,z)=θ當(dāng)且僅當(dāng)x=y=z; (2)D(x,y,z)=D(x,z,y)=D(y,x,z)=···; (3)D(x,y,z)≤D(x,y,a)+D(x,a,z)+D(a,y,z),對(duì)任意x,y,z,a∈X.則D稱為X上的錐D-度量,(X,D)稱為具有Banach代數(shù)的錐D-度量空間. 下面給出一個(gè)具有Banach代數(shù)的錐D-度量空間的例子. 例2.1 設(shè)對(duì)任意的x∈A.定義乘法運(yùn)算為xy(t)=x(t)y(t),t∈[0,1],則A是具有單位元e的Banach代數(shù). 設(shè)P={x∈A:x(t)≥0,t∈[0,1]},則P?A是一個(gè)非正規(guī)體錐[14]. 令X=[0,1],定義映射D:X×X×X×X?→A如下: 則(X,D)是具有Banach代數(shù)A的錐D-度量空間. 定義2.3 設(shè)(X,D)為具有Banach代數(shù)A的錐D-度量空間,x∈X且{xn}為X中的序列,則 (1)稱{xn}收斂于x,若對(duì)任意滿足θ?c的向量c∈A,存在正整數(shù)N,使得D(xm,xn,x)?c對(duì)任意m,n>N成立,記為 (2)稱{xn}為Cauchy列,若對(duì)于任意滿足θ?c的向量c∈A,存在正整數(shù)N,使得D(xn,xn+1,xn+p)?c對(duì)任意n,p≥N成立. (3)稱(X,D)為完備的錐D-度量空間,若(X,D)中的每一個(gè)Cauchy列在(X,D)中都收斂. 定義2.4 設(shè)(X,D)是具有Banach代數(shù)A的錐D-度量空間,稱X是D-有界的,若存在M≥0,使得D(x,y,z)≤M對(duì)任意的x,y,z,a∈X成立,M稱為X的D-有界數(shù). 引理2.4 設(shè)(X,D)是具有Banach代數(shù)A的錐D-度量空間,則 是連續(xù)的.即若 則 引理2.5[14-15]設(shè)E是具有體錐P的Banach空間,若θ≤u?c對(duì)任意θ?c成立,則u=θ. 引理2.6[14-15]設(shè)E是具有體錐P的Banach空間,{xn}∈A.若 則對(duì)任意θ?c,存在正整數(shù)N使得xn?c對(duì)任意n≥N成立. 定義2.5[16-17]設(shè)X是非空集合,映射T,S:X→X,若存在x∈X使得w=Tx=Sx,則稱w是T和S的疊合點(diǎn). 定義2.6[18]設(shè)X是非空集合,映射T,S:X→X稱為弱相容的,對(duì)任意x∈X,如果Tx=Sx,都有TSx=STx成立. 引理2.7[16-17]設(shè)X是非空集合,映射T,S:X→X是弱相容的,若T,S在X中有唯一的疊合點(diǎn)w,即w=Tx=Sx,則w也是T和S的唯一公共不動(dòng)點(diǎn). 定理3.1 設(shè)(X,D)是具有Banach代數(shù)的完備有界的錐D-度量空間,M是X的D-有界數(shù),P是A的非正規(guī)體錐,若映射T,S:X→X滿足 對(duì)任意的x,y,z∈X,其中α,β ∈P且 0≤ ρ(α)+ρ(β)<1,α,β可互換,此外,設(shè)有 (1)T(X)?S(X); (2)S(X)是X的閉子空間; (3)(T,S)是弱相容的. 則T,S在X中有唯一的公共不動(dòng)點(diǎn). 證明任選x0∈X,由T(X)?S(X),可構(gòu)造序列{xn}和{yn}滿足 不妨設(shè)ynyn+1,n∈N,下證{yn}是 Cauchy列. 對(duì)任意的z∈X,有 由此得到 令λ=α+β,同理,有 依次進(jìn)行此過程,可得 對(duì)任意固定的P∈N,存在yn+p∈X使得 又因?yàn)?/p> 由注記 2.1,可得→0(n→∞). 由于M是X的D-有界數(shù),故 故由引理 2.6知,對(duì)任意c∈A且θ?c,存在正整數(shù)N使得對(duì)任意的n>N時(shí),有θ≤D(yn,yn+1,yn+p)?c成立. 因此,{yn}是X中的Cauchy列.由于S(X)是完備空間X的閉子空間,故S(X)也是完備的,因而存在u∈S(X)使得,從而,下證u是T,S的唯一的疊合點(diǎn). 由于u∈S(X),知存在q∈X使得Sq=u.首先證Tq=Sq=u.因?yàn)镈是連續(xù)的,所以有 又D(Tq,Sq,Sq)=D(Tq,u,u),故 (e?β)D(Tq,u,u)≤θ. 于是D(Tq,u,u)=θ,因此Tq=u=Sq,即u為T,S的疊合點(diǎn).下證u的唯一性,不妨設(shè)v=Tq′=Sq′為T,S的另一疊合點(diǎn),有 化簡(jiǎn)得 (e?α)D(u,v,u)≤θ.故D(u,v,u)=θ,即u=v.所以u(píng)是T,S的唯一的疊合點(diǎn).根據(jù)引理2.7,由T,S的弱相容性,知u是T,S的唯一的公共不動(dòng)點(diǎn). 定理3.2 設(shè)(X,D)是具有Banach代數(shù)的完備有界的錐D-度量空間,M是X的D-有界數(shù),P是A的非正規(guī)體錐,對(duì)任意的x,y,z∈X,若自映射T,S:X→X滿足 對(duì)任意的x,y,z∈X,其中α,β,γ∈P且 0≤ρ(α)+ρ(β)+ρ(γ)<1,α,β,γ可互換,此外,設(shè)有(1)T(X)?S(X);(2)S(X)是X的閉子空間;(3)(T,S)弱相容的.則T,S在X中有唯一的公共不動(dòng)點(diǎn). 證明任意選定x0∈X,由T(X)?S(X),可構(gòu)造迭代序列{xn}和{yn}滿足 不妨設(shè)ynyn+1,n∈N,下證{yn}是 Cauchy列. 對(duì)任意的n,p∈N,有 于是推出 令 依次進(jìn)行此過程,有D(yn,yn+1,yn+p)≤λnD(y0,y1,yp). 由于M是X的D-有界數(shù),故又 由引理2.6知,對(duì)任意θ?c且c∈A,存在正整數(shù)N使得對(duì)任意n≥N時(shí),有 故{yn}是X中的Cauchy列,由X的完備性,S(X)是X的閉子空間知S(X)是完備的,從而存在u∈S(X)使得,也有,下證u是T,S的唯一疊合點(diǎn).由u∈S(X)知存在q∈X使得Sq=u,首先證明Tq=Sq=u,有 由D的連續(xù)性,令n→∞,上式兩端同時(shí)取極限,可得 可推得 (e? γ)?1D(u,u,Tq)≤θ.因此,D(u,u,Tq)=θ,于是Tq=u=Sq.即u為T,S的疊合點(diǎn),下證u是唯一的,不妨設(shè)v=Tq′=Sq′是T,S的另一疊合點(diǎn),則有 化簡(jiǎn)得 (e?α?β?γ)D(Tq,Tq,Tq′)≤θ.則D(Tq,Tq,Tq′)=θ,即u=Tq=Tq′=v,故u是T,S的唯一的疊合點(diǎn). 又因?yàn)門,S是弱相容的,即當(dāng)u=Tu=Su,有TSu=STu.故由引理2.7知u是T,S的唯一的公共不動(dòng)點(diǎn). 推論3.1 設(shè)(X,D)是具有Banach代數(shù)的完備有界的錐D-度量空間,M是X的D-有界數(shù),P是A的非正規(guī)體錐,若自映射T,S:X→X,m,t為正整數(shù),滿足 對(duì)任意的x,y,z∈X,其中α,β∈P且 0≤ρ(α)+ρ(β)<1,α,β可互換,此外,設(shè)有 (1)Tm(X)?St(X);(2)St(X)是X的閉子空間;(3)(Tm,St)是弱相容的.則T,S在X中有唯一的公共不動(dòng)點(diǎn). 證明由定理2.1知,Tm和St有唯一的公共不動(dòng)點(diǎn)u.當(dāng)m=1時(shí),Tu=Stu=u,由條件(3)知,TStu=StTu,所以有Tm(Tu)=T(Tmu)=Tu=T(Stu)=St(Tu),上式說明Tu為Tm,St的公共不動(dòng)點(diǎn).由u的唯一性,可得Tu=u. 同理,Su=u.故T,S有唯一的公共不動(dòng)點(diǎn). 推論3.2 設(shè)(X,D)是具有Banach代數(shù)的完備有界的錐D-度量空間,M是X的D-有界數(shù),P是A的非正規(guī)體錐,若自映射T,S:X→X,m,t為正整數(shù),滿足 對(duì)任意的x,y,z∈X,其中α,β∈P且 0≤ρ(α)+ρ(β)+ρ(γ)<1,α,β可互換,此外,設(shè)有 (1)Tm(X)?St(X);(2)St(X)是X的閉子空間;(3)(Tm,St)是弱相容的.則T,S在X中有唯一的公共不動(dòng)點(diǎn). 證明類似于推論3.1.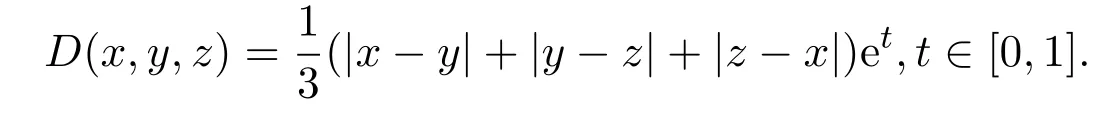
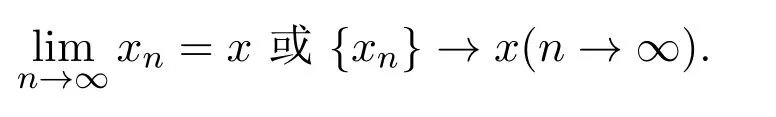
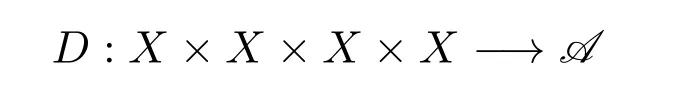
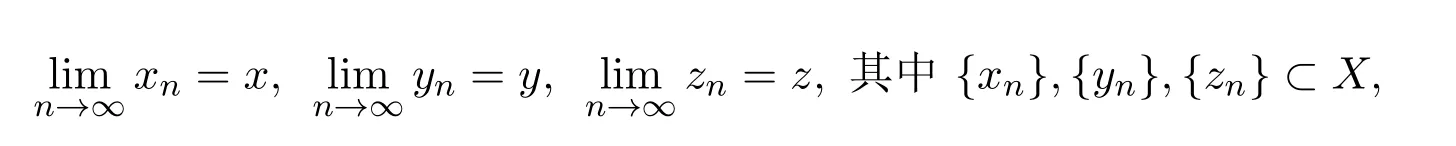
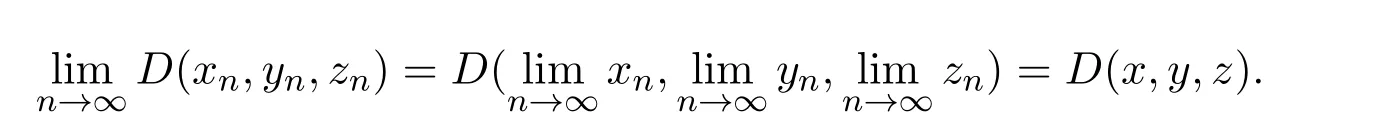
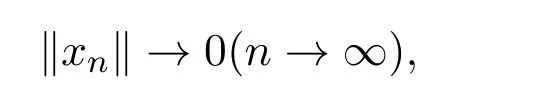
3 主要結(jié)果及其證明