基于迭代正則化高斯-牛頓法的非線性Urysohn積分方程數值解

陳亞文,仝云莉,閔濤

(西安理工大學理學院,陜西 西安 710054)

1 引言

在物理學、力學和工程技術諸多領域都存在大量的非線性不適定問題,例如參數識別問題、逆散射問題、逆位勢問題以及第一類Fredholm積分方程求解問題等[1].這類問題一般歸結為求解下面的非線性不適定算子方程:

其中,F:D?X→Y是定義域為D的非線性算子,X,Y為Hilbert空間.當(1)式的解不連續依賴于右端數據y時,稱(1)式為不適定的.在實際問題中,右端數據y通常是由測量得到的,因而得到的數據是一個滿足∥yδ?y∥≤δ的近似數據yδ,這里δ>0是給定的很小的擾動水平[2-4].

一個典型的例子就是Urysohn型非線性算子方程[5]:

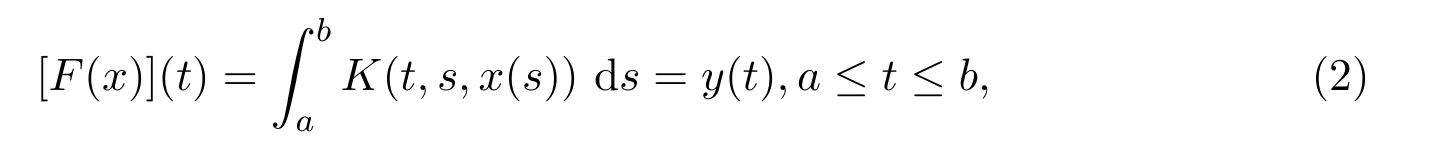
這里x(s)未知,K(t,s,x(s))為定義在 [a,b]×[a,b]×R上的核函數,且非線性依賴于x(s).

由于上述問題的不適定性,為了獲得穩定的、準確的數值解,就必須使用正則化方法.本文利用迭代正則化高斯-牛頓法求解問題(1)或問題(2).此外,采用Sigmoid-型函數確定正則化參數,由于Sigmoid-型函數的性質,隨著迭代次數的增加,函數值不斷減小并逐漸趨于0,以此來確定一個最佳的正則化參數.

2 迭代正則化高斯 -牛頓法

設方程(1)有解x?(不必唯一),yδ是y的擾動,

如用牛頓法求解方程(1),則由線性化方程

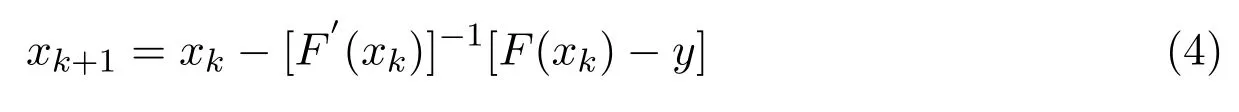
確定xk+1.一般情況下,F′是不可逆的,需要通過正則化方法來求得其解x?的近似.

為此,可定義泛函

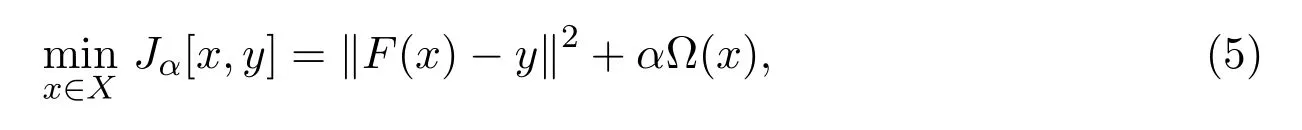
其中,α>0為正則化參數,?(x)為先驗條件.要求無約束最優化問題(5)的解,首先將算子F線性化,利用F(x)在第k次迭代點xk處的泰勒展開式,得到

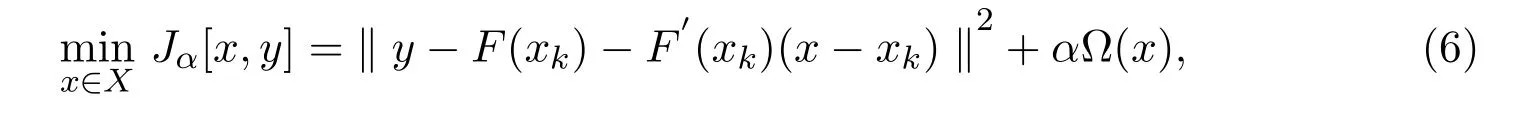
其中?(x)=∥L(x?x0)∥為穩定泛函,L是單位矩陣(L=L0=I∈Rn×n)或者是一階算子的離散近似,即 [L1]ij=δi,j?δi,j?1,i=1,2,···,n?1,其中,δi,j為克羅內克符號,j=1,2,···,n,方程(6)通過一階最優條件求解,可得到:

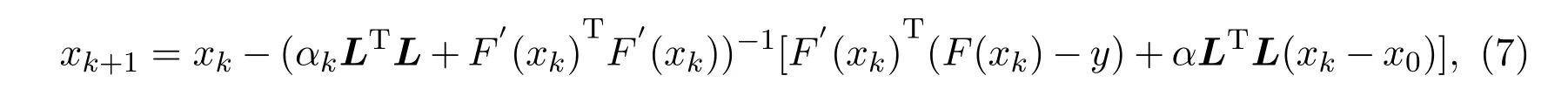
(7)式稱為迭代正則化高斯-牛頓法[6-7],簡記為IRGN法.αk表示正則化參數且為單調遞減序列并滿足:

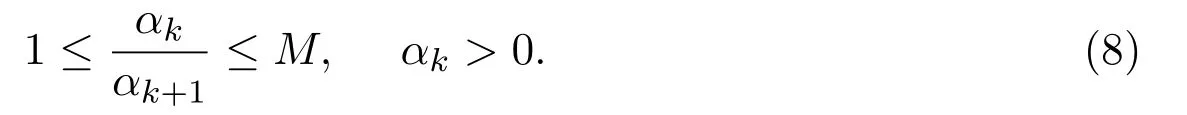
正則化參數的選取規則(8)是保證正則化方法收斂的必要條件,即當擾動水平趨于0時,正則解收斂到真解.有關此迭代算法的收斂性定理的證明可參考文獻[8-12].

3 離散化

為了數值求解(2),需要將其離散化,離散化的方法有很多,這里采用梯形公式進行離散.將(7)式改寫為如下形式:

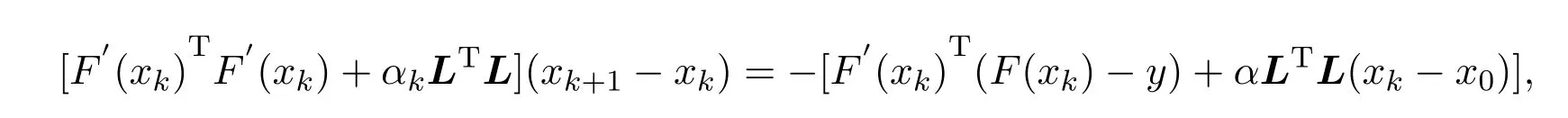
要得到F′(xk)TF′(xk),需要求解非線性算子F的 Fréchet導數.

令K(t,s,x(s))為定義在a≤t,s≤b,|x|≤r上的函數,并設

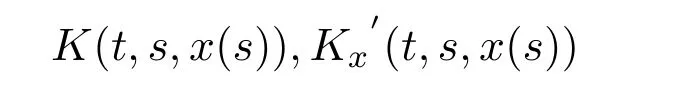
處處連續.積分算子F為[a,b]上的連續函數,并且在開球上Fréchet可導,對任意的x0∈C[a,b]且,h∈C[a,b],可得到F的 Fréchet導數為:

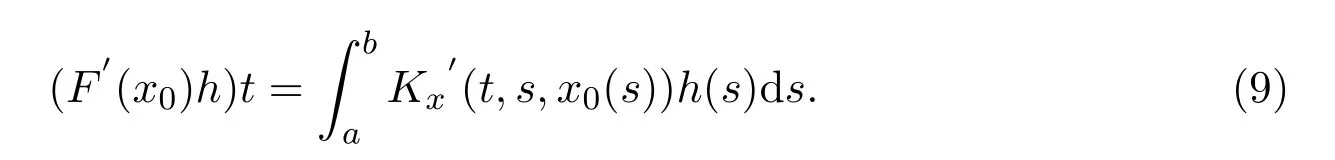
上述(9)式定義的算子是[a,b]上的線性連續算子.

事實上,對于確定的θ=θ(h)∈[0,1],有

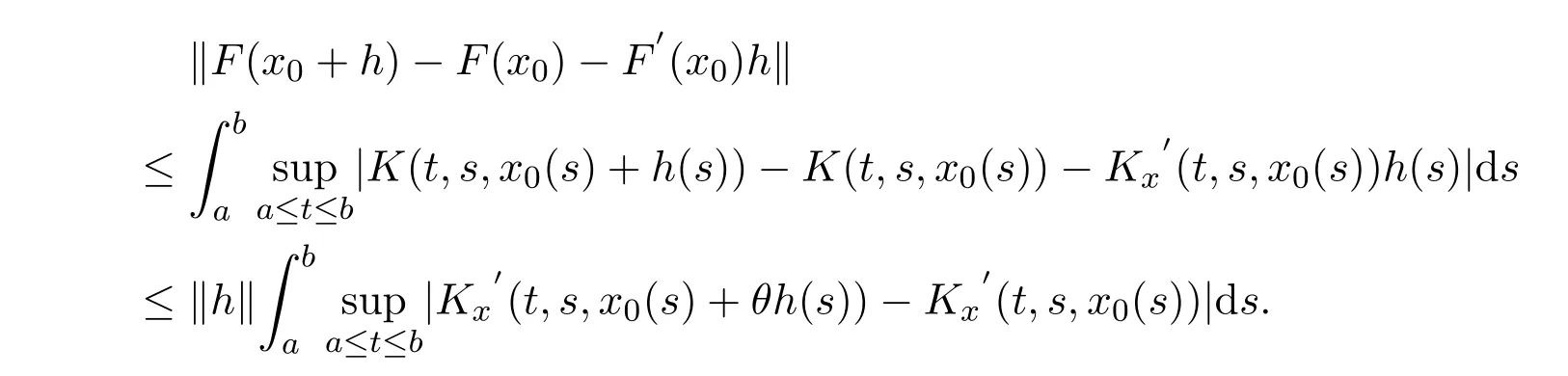
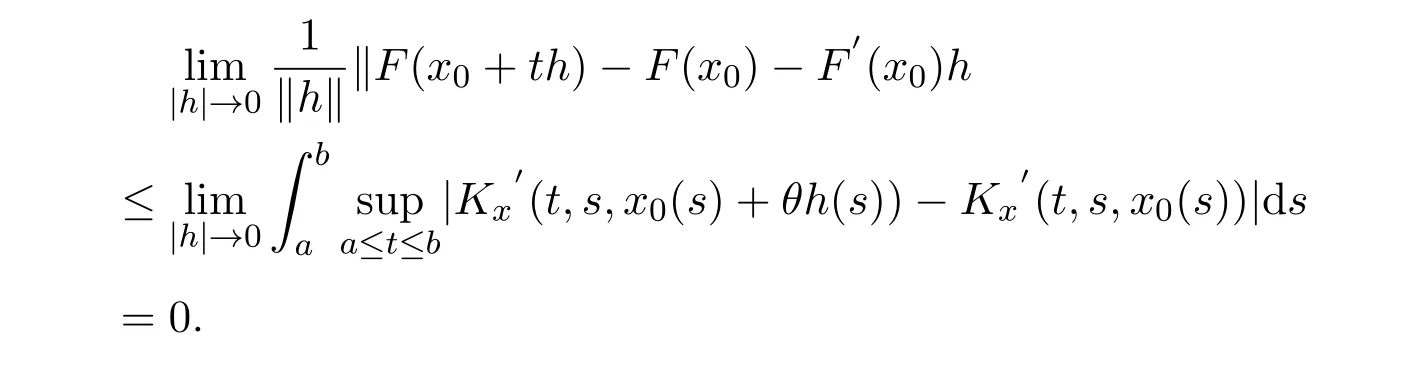
因此F的Fréchet導數可以通過(9)式得到.

利用梯形公式將方程(9)進行離散:把區間[a,b]等分成N個小區間,其步長為

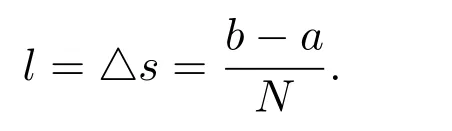
令s0=a,sj=a+j△s,同理

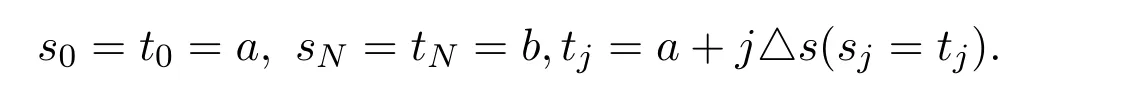
設x(sj)=xj,則有

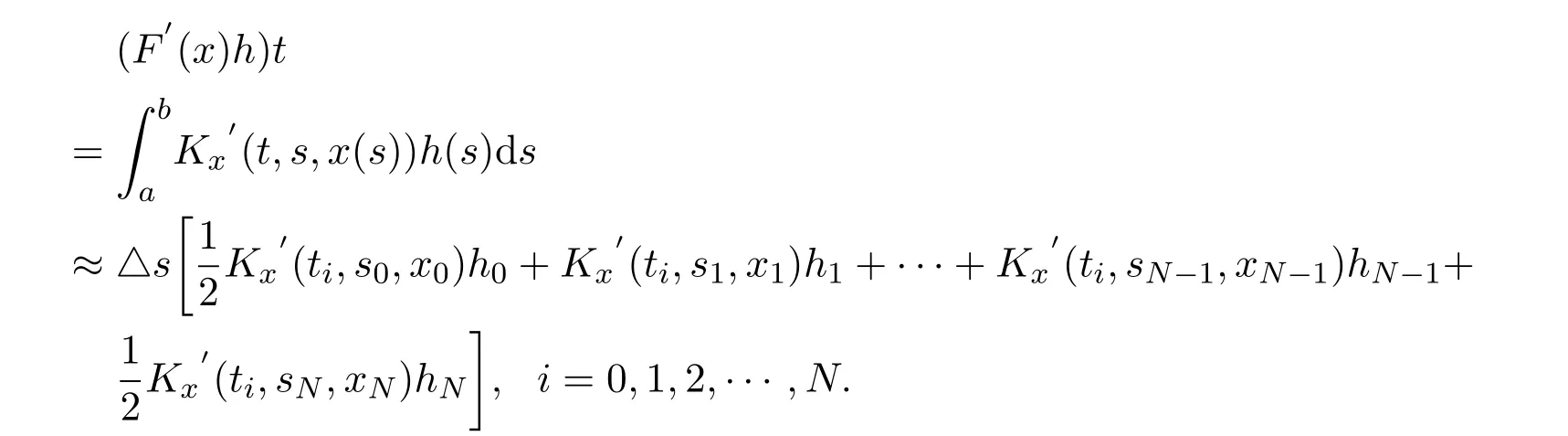
改寫成矩陣形式為:

其中

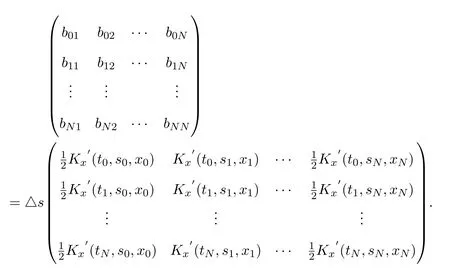
利用迭代正則化高斯-牛頓法可得到:

其中

因此得到迭代格式x(k+1)=x(k)+h(k),通過此格式便可求出(2)的近似解.

實現上述算法的關鍵在于選擇合適的正則化參數αk.本文基于Sigmoid-型函數的性質,按如下方法選取正則化參數:按照(11)式選擇的正則化參數,不難驗證其滿足下列條件:

可以看到,根據上述正則化參數的選取方法,在迭代開始時能夠充分對問題進行正則化,然后隨著迭代數的增加正則化參數逐漸減小,達到解穩定的目的.

4 數值模擬

考慮重力測定中的一個實際問題[13-15].它在地球物理反演中經常遇到,是一個典型的研究問題.設有一物體,其密度與環繞其周圍的介質的密度不同.問題是通過測定由于重力場作用產生的隅角來判斷物體的形狀.

假設地面下 (z=0)介質的密度分布不均勻,為簡單計,設有兩種密度分布ρ1和ρ2,它們被一邊界z(x)隔開(見圖1).

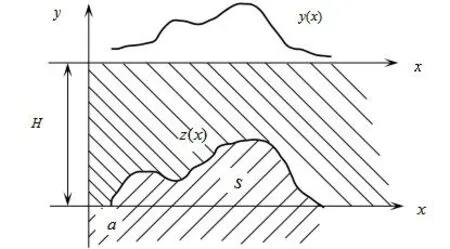
圖1 重力測定原理圖

在如此的設定下,由于重力場的作用,可以在地表測得一隅角為其中V是由于密度差ρ=ρ2?ρ1引起的位勢.

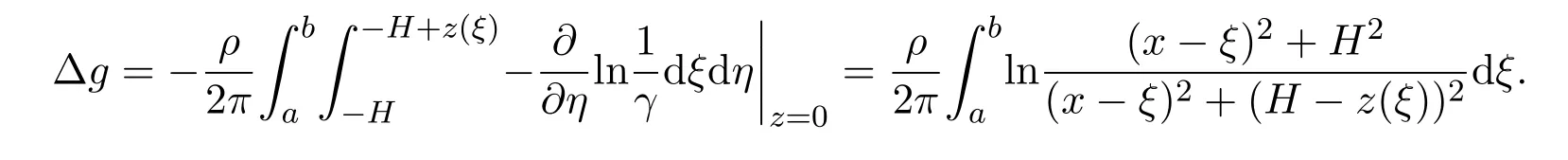
而隅角?g是可以測定的,于是問題就是要確定邊界z(x).這就化歸為求解如下的非線性Urysohn積分方程:

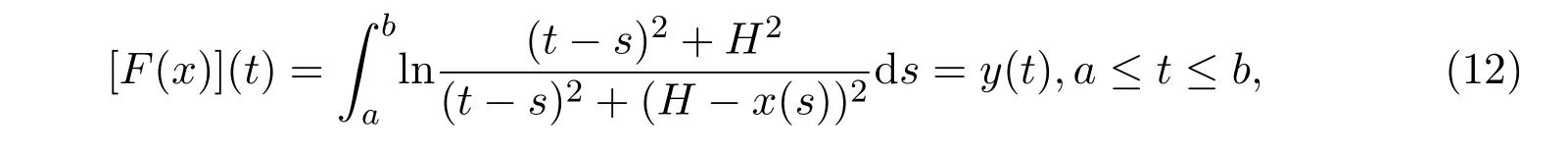
其中F是一個非線性算子.

在數值求解之前,先做如下規定:

1.用L∞表示誤差范數,即

2.用RE表示相對誤差,即

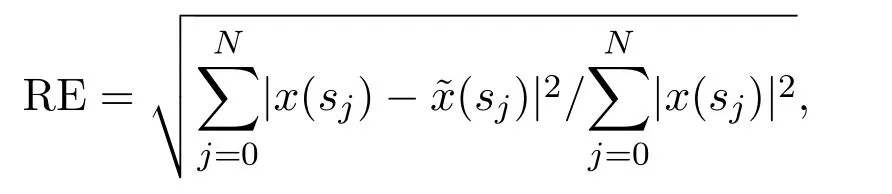
其中,sj為節點,N為區間[a,b]上均勻分布的節點的個數,x(s)為精確解,為數值解.

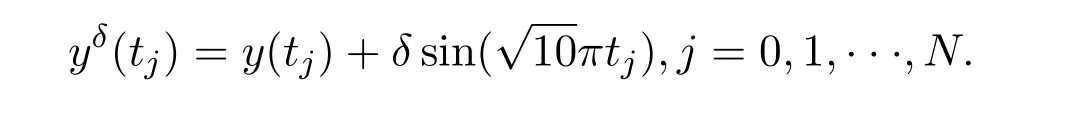
數值模擬 (12)式,取 [a,b]=[?1,1],H=2,N=100,L=L1,迭代次數選為 15,若正則化參數取為 0時,解的相對誤差達到 8.734 983 656 596 983e+006,計算結果嚴重失真.因此需要正則化處理,本文選取正則化參數為:,初始猜測x(0)=(0.5,0.5,···,0.5),擾動分別為δ=0,0.005,0.01,0.05時,相應的L∞和 RE分別如表1所示,當δ=0,δ=0.05時精確解與數值解的比較如圖2和圖3所示.迭代次數選為40,δ=0.05時相對誤差隨迭代次數的變化如圖4所示,迭代次數選為15,當δ=0.05時相對誤差隨迭代次數的變化如圖5所示.

表1 同一初始猜測、不同擾動、相同迭代數下所得誤差比較

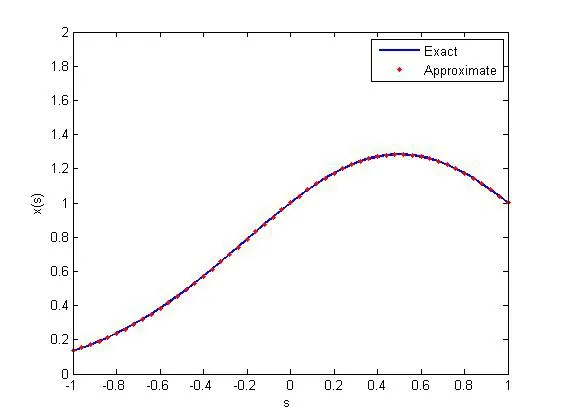
圖2 迭代正則化牛頓法所得精確解與數值解的比較,δ=0

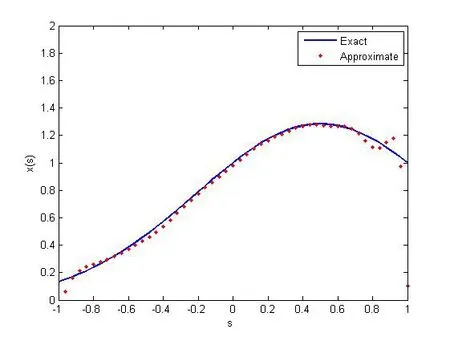
圖3 迭代正則化牛頓法所得精確解與數值解的比較,δ=0.05

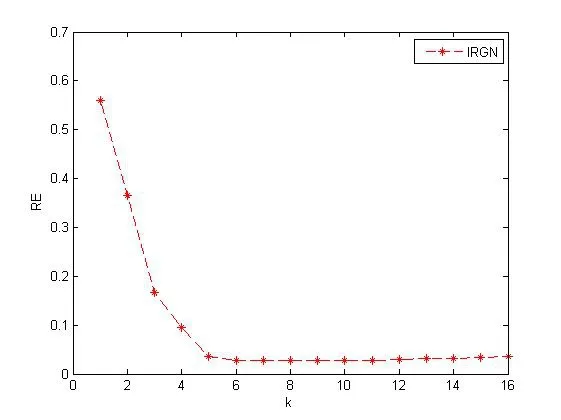
圖4 迭相對誤差隨迭代次數的變化,δ=0.05

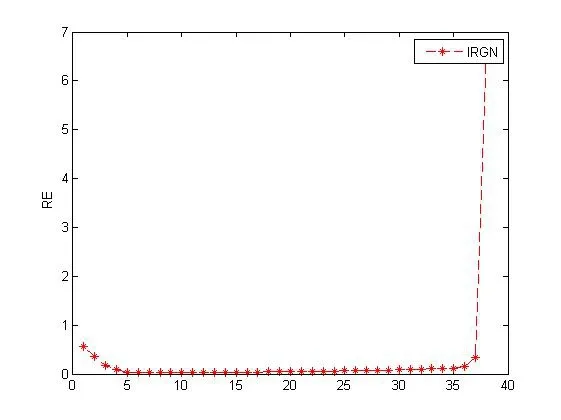
圖5 迭相對誤差隨迭代次數的變化,δ=0.05

取迭代次數K=15,擾動δ=0.05時,不同的初始猜測所得誤差如表2所示:

表2 不同初始猜測、同一擾動、相同迭代數下所得誤差比較

取初始猜測x(0)=(0.5,0.5,···,0.5),擾動δ=0.05時,不同的迭代次數所得誤差如表3所示:

表3 相同初始猜測、同一擾動、不同迭代數所得誤差比較

從表1可以看出,在初始猜測不變,迭代數相同的情況下,隨著擾動的增加,求解誤差相對較小,解的穩定性和準確性更高,具體比較見圖2和圖3.此外,由圖4可知,當迭代開始時誤差急劇下降,然后趨于平緩,當迭代次數增加時,又出現相對誤差變大情況,即半收斂現象,見圖5.在實際應用時,可以通過誤差限選取迭代次數.從表2可以看出,在擾動水平相同、迭代數相同的情況下,隨著初始猜測的變化,相對誤差幾乎不變,說明在一定的范圍內初始猜測對解的影響不大;從表3可以看出,在初始猜測不變、擾動水平相同的情況下,隨著迭代數的增加,相對誤差有所增加,但精度還是可以接受的.

5 結論

本文采用迭代正則化高斯-牛頓法求解非線性Urysohn積分方程,通過對重力測定中的一個實際問題進行數值模擬,結果表明:迭代正則化高斯-牛頓法在求解此類問題時具有誤差小,數值解的穩定性、準確性較高的優點.