割補法在三視圖還原空間幾何體中的應用

安徽省蕪湖市沈巷中學

何業亮 (郵編：241012)

三視圖是高中新教材新增內容，也是高考的常考知識點．不難發現，由三視圖還原幾何體的試題經“考”不衰，且其載體的復雜程度呈增加之勢，特別是以簡單組合體為載體的試題備受命題專家親睞．雖然很多學生能將“長對正，高平齊，寬相等”爛記于心，也對簡單幾何體的三視圖了如指掌，但處理這類問題仍力不從心，無法可依，甚至不少教師的講解和很多資料的答案往往是直接告知幾何體，不作詳細解釋．筆者經過深入研究，發現割補法(對三視圖進行分割或修補)能有效處理復雜的三視圖還原幾何體問題，且簡單易行，直觀明了．

1 合理分割，各個擊破

例1(2015·重慶·文5)某幾何體的三視圖如圖1所示，則該幾何體的體積為( )

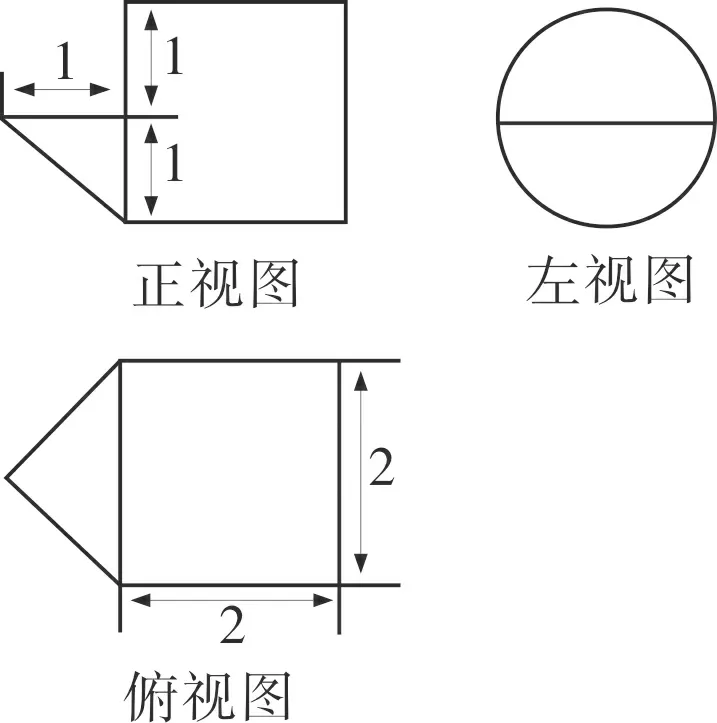
圖1

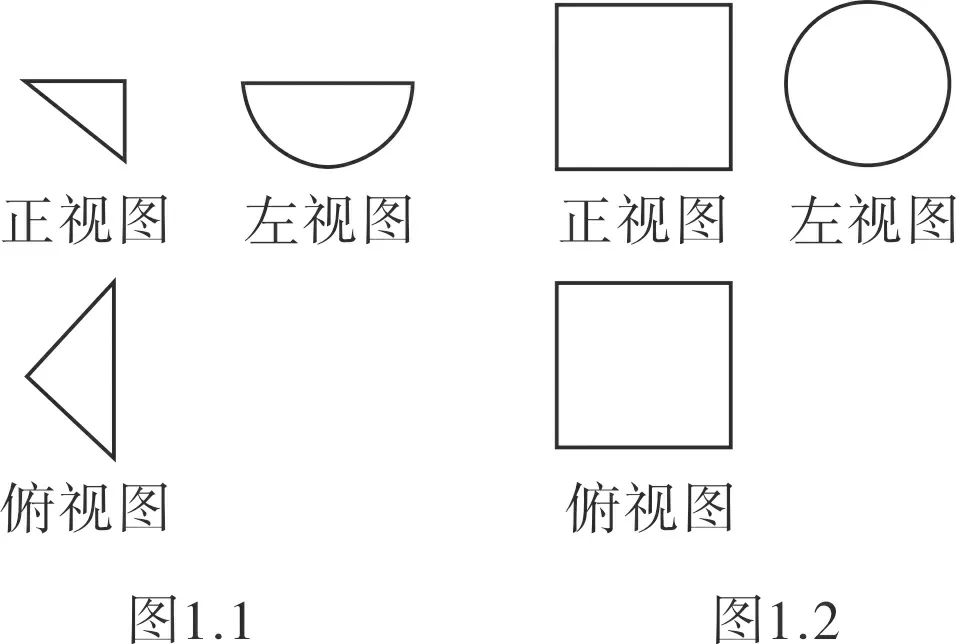
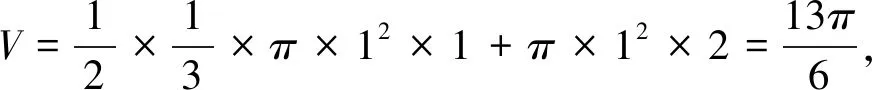
例2(2014·安徽·理7)一個多面體的三視圖如圖2所示，則該多面體的表面積為( )

解析此題易被正方形中的虛線和實線所迷惑，從而無法得出該多面體的直觀圖．我們可以將三視圖分割成三部分后重新組合，如圖2.1-2.3所示．

圖2

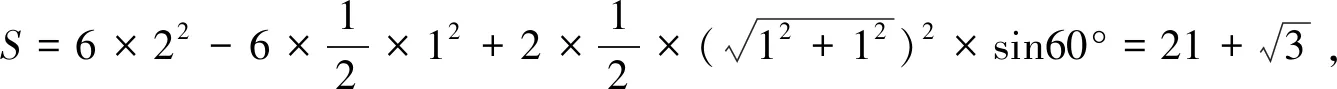
評述在“長對正，高平齊，寬相等”的前提下，可將一些復雜的三視圖分割成若干個熟悉幾何體或簡單幾何體的三視圖，后將所得的那些幾何體進行符合題意的組合，即可得所求幾何體.

2 恰當修補，無中生有

例3(2014·重慶·理7)某幾何體的三視圖如圖3所示，則該幾何體的表面積為( )

A.54 B.60 C.66 D.72

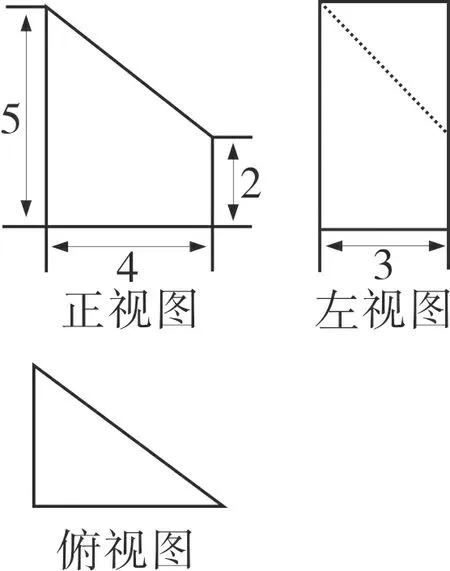
圖3

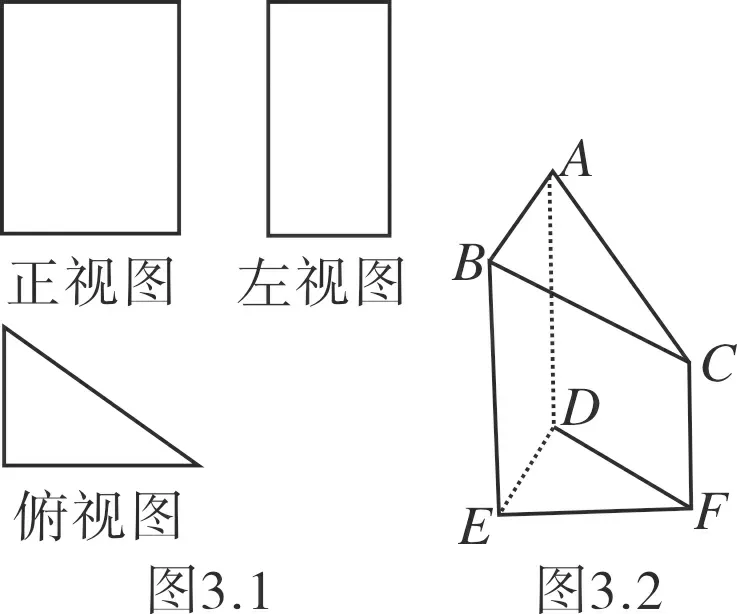
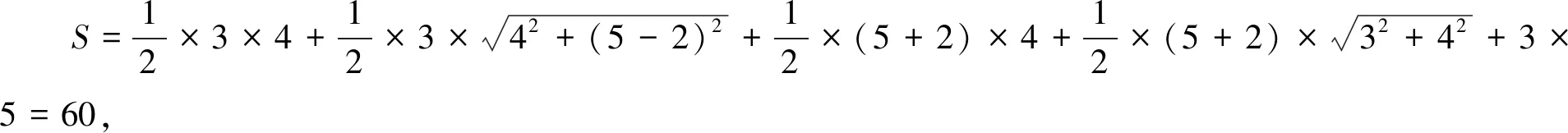
例4(2012·湖北·理4)已知某幾何體的三視圖如圖4所示，則該幾何體的體積為( )

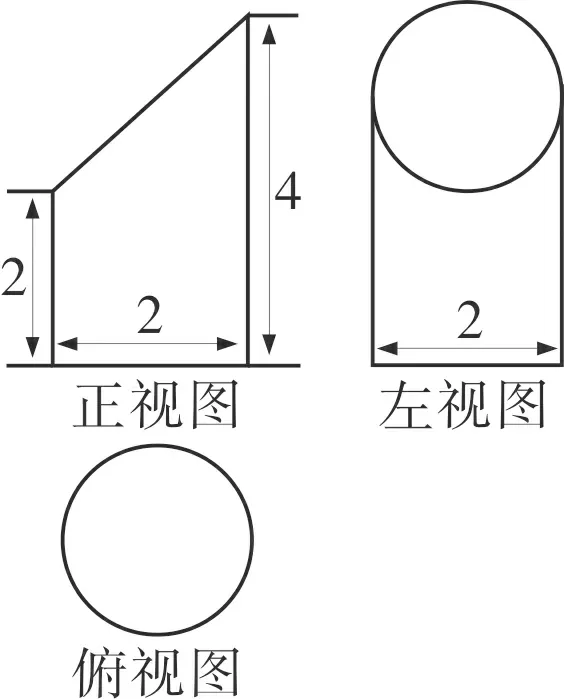
圖4

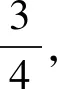
評述本著“長對正，高平齊，寬相等”的原則，可將有些三視圖修補成一個簡單幾何體或熟悉幾何體的三視圖，然后在所得幾何體上進行恰當的添補或剪裁，直到得到符合題設的幾何體．

3 割補合用，雙管齊下

例5(2014·遼寧·理7)某幾何體的三視圖如圖5所示，則該幾何體的體積為( )

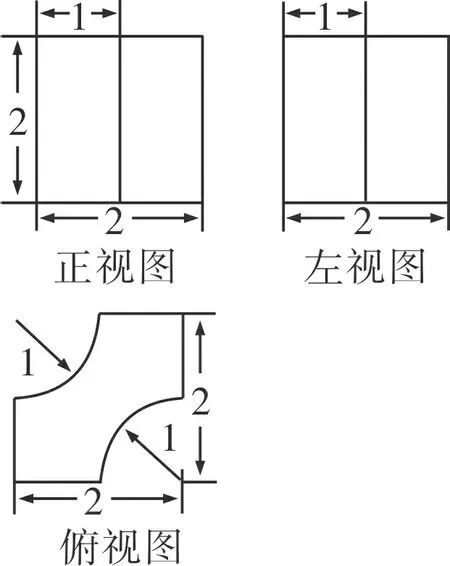
圖5

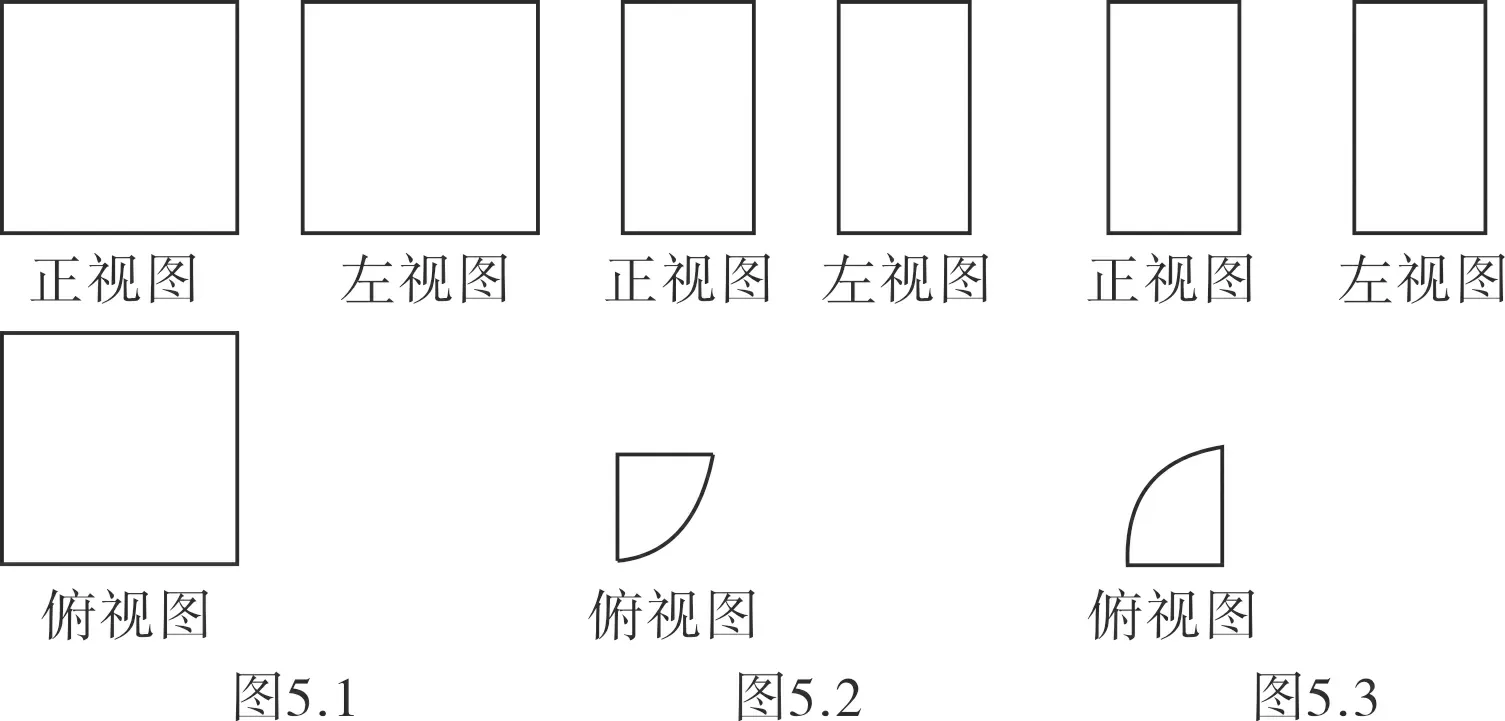
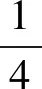
評述有些三視圖還原幾何體的問題，可對三視圖進行分割和修補，這樣能有效地轉化為熟悉幾何體的三視圖，但是一定要遵循“長對正，高平齊，寬相等”的原則，否則對后續幾何體的確定不利．

由此可見，處理復雜的三視圖還原空間幾何體問題，割補法有著奇效，可以化陌生為熟悉，化復雜為簡單．