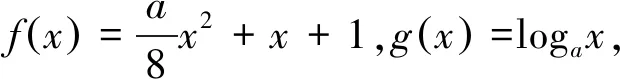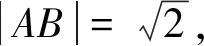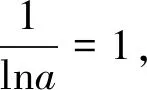動點到動點距離最值的求解策略

上海市松江一中

董頂國 (郵編：201600)

上海市嘉定二中

牟忠智 (郵編：201802)

距離問題為大家熟知，動點到定點距離、動點到定直線距離、動點到動點距離常常成為高考命題的第一視角得到青睞.前兩種距離有模式可尋，但對于動點到動點距離，學生頗感棘手.下面筆者對該問題從不同角度進行靈活化歸，化“動”為“靜”，煥發新的活力.

1 利用反函數圖象的對稱化歸為點到直線的距離

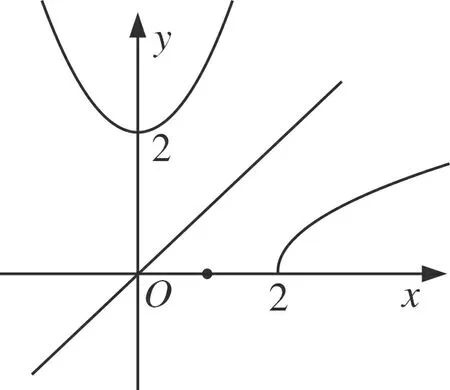
圖1

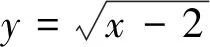
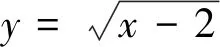
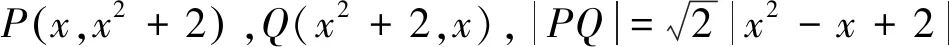
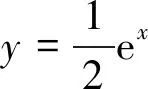
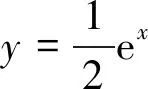
點評該類問題重在從對稱中尋求突破，事實上，只要是兩曲線(也可能是曲線部分)關于某直線對稱，則兩曲線上動點距離最值問題通常可劃歸為一曲線上動點到該線的距離最值問題.

2 利用圓的性質轉化為動點到定點距離

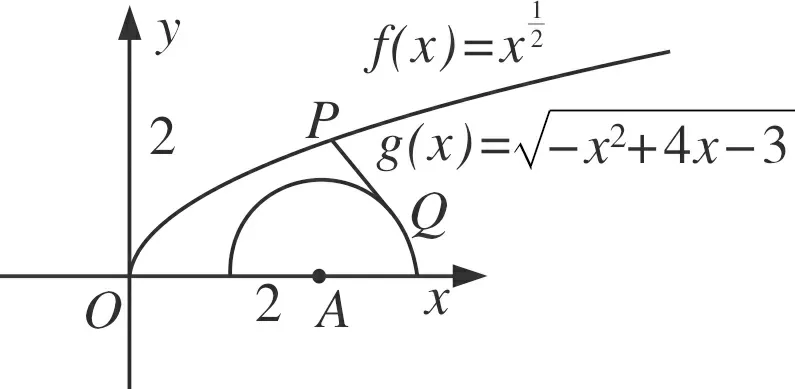
圖2

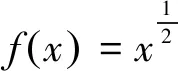
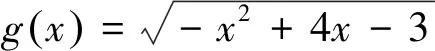
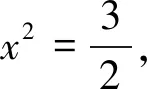
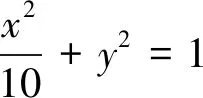
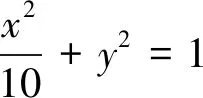
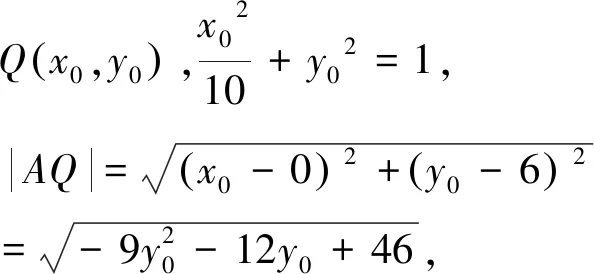
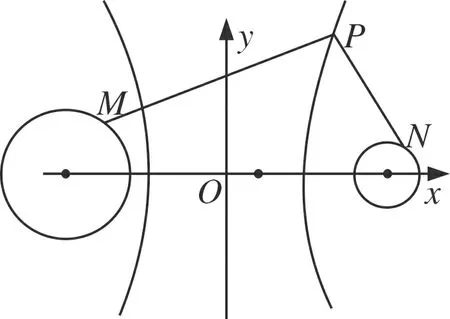
圖3

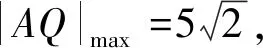
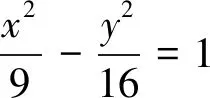
解題分析(|PM|-|PN|)max=|PM|max-|PN|min.設圓(x+5)2+y2=4的圓心為F1(-5,0)，設圓(x-5)2+y2=1的圓心為F2(5,0),|PM|max=|PF1|+2,|PN|min=|PF2|-1，所以(|PM|-|PN|)max=|PM|max-|PN|min=|PF1|+2-(|PF2|-1)=(|PF1|-|PF2|)+3=9.

點評該類問題的核心是利用圓的幾何性質，把兩動點距離劃歸為動點到圓心的距離問題，減少了變量個數，簡化了思考過程.

3 利用線的平移化歸線與曲線關系

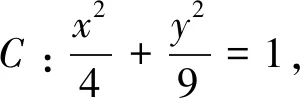
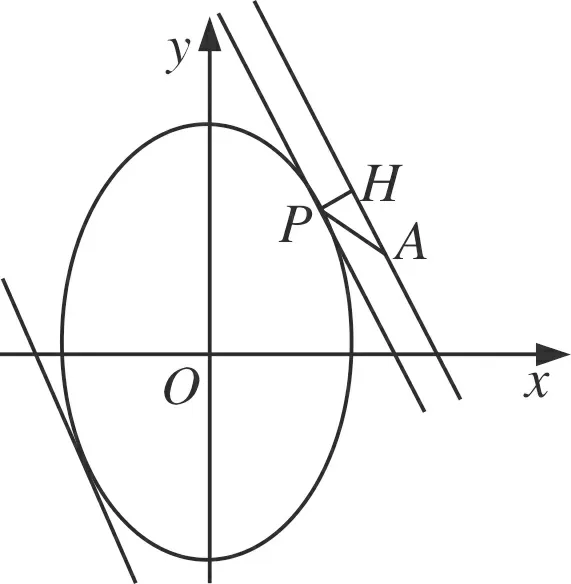
圖4

(Ⅰ)寫出曲線C的參數方程，直線l的普通方程；(Ⅱ)過曲線C上任一點P作與l夾角為30o的直線，交l于點A，求|PA|的最大值與最小值.

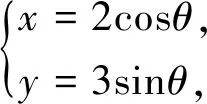
(Ⅱ)作PH⊥l于點H，|PA|=2|PH|，|PA|的最值問題即|PH|的最值問題，最值點P即為與l平行的橢圓切線的切點，|PA|的最值化歸為切線與直線l的距離問題.

設切線方程為y=-2x+m，帶入橢圓方程得25x2-16mx+4m2-36=0.

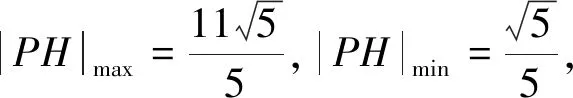
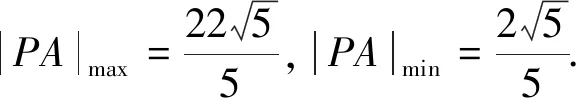
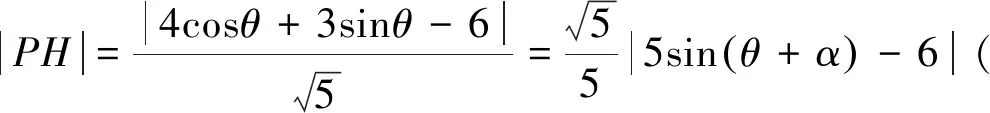
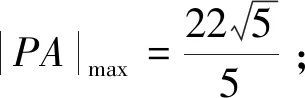
4 利用動點“依托”關系，建模化歸函數最值

較多的問題中兩動點不是隨意變化，而總是存在某種依存關系，利用這種依存關系，恰當引入變量建模求解.

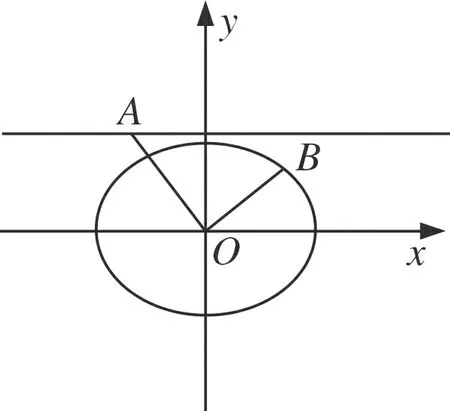
圖5

例4(2014北京高考卷)已知橢圓C:x2+2y2=4.

(1)求橢圓C的離心率；(2)設O為原點，若點A在直線y=2，點B在橢圓C上，且OA⊥OB，求線段AB長度的最小值.

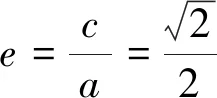
(2)設點A、B的坐標分別為(t,2),(x0,y0),其中x0≠0.

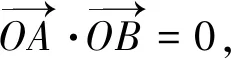
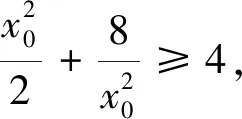
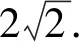
點評該問題通過動點坐標關系的建立，減少參量個數，利用曲線方程中的坐標關系代換，借助曲線范圍，較好構建函數模型求解.再如：

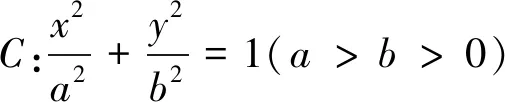
(I)求橢圓C的方程；(Ⅱ)求線段MN的長度的最小值；(Ⅲ)略.

圖6

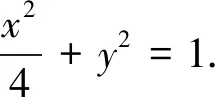
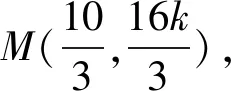
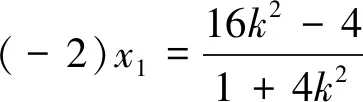
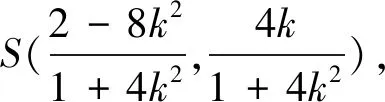
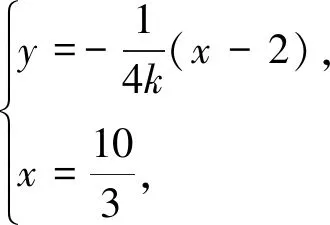
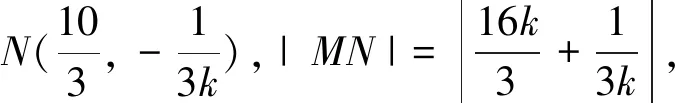
點評該問題中動點距離雖受曲線上動點的直接制約，但動點均為線線交點，結合實際問題，恰當的引入AS的斜率k,構建關于k的函數簡捷求解.

5 借助導數工具，尋求轉換條件

對于分別在兩函數圖象上的動點，其距離的常見轉化無法實施時，常借助導數這一工具，化歸切線間的距離求解.