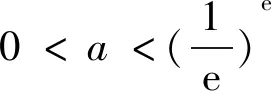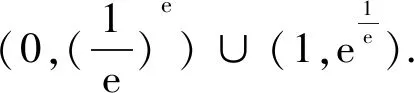對一道安慶“二模”試題的異議
安徽省樅陽縣宏實中學
朱賢良 (郵編:246700)
2019年3月21-22日,是安慶市高三“二模”考試時間.由于命題細致考究(安慶“二模”有專門的命題組)、參考學生眾多(整個安慶地區及周邊市縣的部分高三學生參加考試)、時間節點恰當(一輪復習即將結束、二輪復習即將開始)等原因,其考試成績具有重要的分析與參考價值,因此每年的安慶“二模”都備受重視.理科數學第12題引起了筆者的關注與思考.
1 試題與參考答案
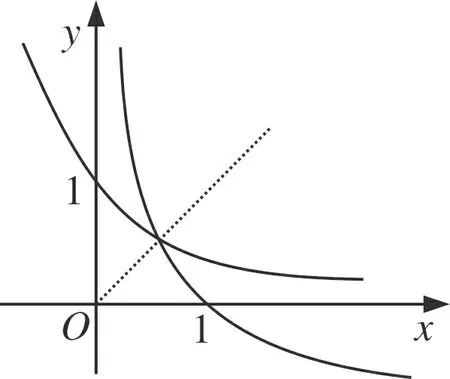
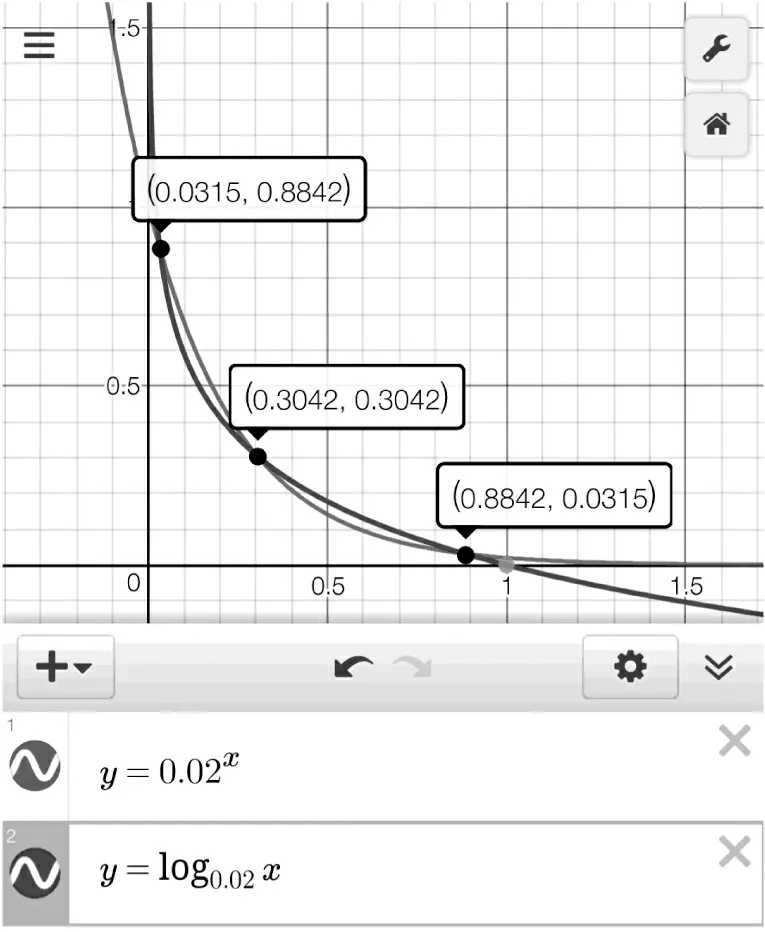
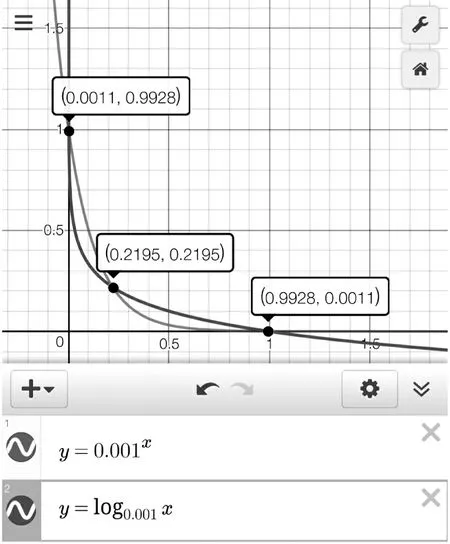
題目(2019年安慶“二模”·理12)若函數f(x)=logax(a>0且a≠1)的定義域與值域都是[m,n](m A.(1,+∞) B.(e,+∞) 參考答案函數f(x)=logax的定義域與值域相同等價于方程logax=x有兩個不同的實數解. 圖1 圖2 不難發現,上述兩種解法實際上都是建立在“a>1”這一前提下的,其本質是研究a>1時,y=logax與y=x的交點個數問題,也就是函數y=ax與y=logax的交點個數問題.而未對“0 即m=an=logan.同理可得n=am=logam.問題歸結為方程ax=logax的兩個不等實根m、n,即曲線y=ax與y=logax至少存在兩個不同交點(注意:由于m=an=logan 圖3 圖4 同底的指、對數函數的圖象的交點個數問題是一個極易犯錯的問題,其研究與分析在中學數學期刊上并不鮮見.許多師生認為0 事實真的如此嗎?借助畫圖軟件,繪制了底數a=0.02時的函數y=ax與y=logax的圖象,如圖4所示.根據圖象可以看出,y=0.02x與y=log0.02x的圖象共有三個交點,其中有兩個交點(0.0315,0.8842)與(0.8842,0.0315)(橫、縱坐標為四舍五入后的近似值)不在直線y=x上,即函數f(x)=log0.02x在區間(0.0315,0.8842)上的值域也是(0.0315,0.8842).再以底數a=0.001為例繪制函數圖象(圖5),函數f(x)=log0.001x在區間(0.0011,0.9928)上的值域還是(0.0011,0.9928). 圖5 因此,本題的四個選項均不正確,其根源在于對同底數的指、對數函數圖象的交點個數存在錯誤的認知.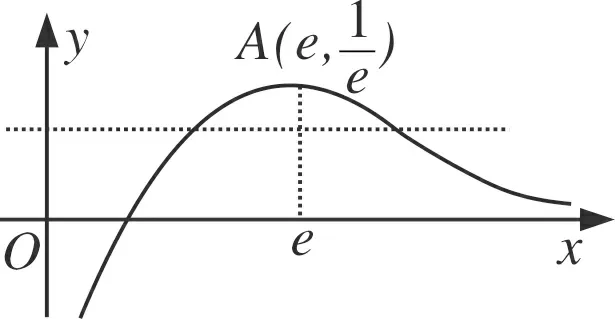
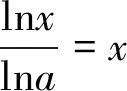
2 圖象法另解
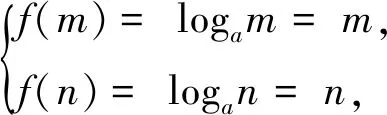
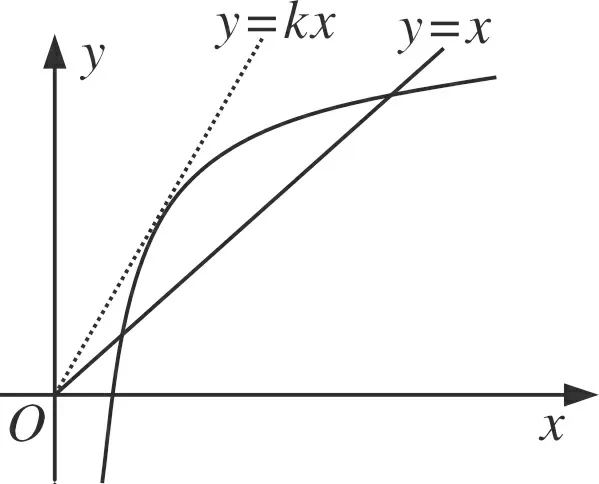
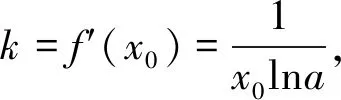
3 被遺忘的情形
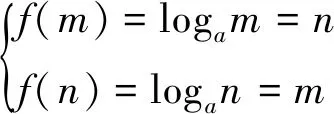
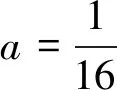
4 正解