高考立體幾何解答題復(fù)習(xí)的深度思考

浙江省慈溪實(shí)驗(yàn)高級(jí)中學(xué)

許建芳 (郵編：315300)

數(shù)學(xué)家波利亞在《數(shù)學(xué)與猜想》中提到：“數(shù)學(xué)有兩個(gè)側(cè)面……用歐幾里得的方式提出來(lái)的數(shù)學(xué)是一門系統(tǒng)的演繹科學(xué)；但在創(chuàng)造過(guò)程中的數(shù)學(xué)卻是實(shí)驗(yàn)性的歸納科學(xué).”不同的推理形式有不同的特點(diǎn)和功能，要注意他們之間的有機(jī)融合.通過(guò)立體幾何的學(xué)習(xí)，學(xué)生能掌握邏輯推理的基本形式，學(xué)會(huì)有邏輯地思考問(wèn)題：能夠在比較復(fù)雜的情景中把握事物發(fā)展的脈絡(luò)；形成重論據(jù)、有條理、合邏輯的思維品質(zhì)和理性精神，增強(qiáng)交流能力.通過(guò)立體幾何的學(xué)習(xí)，學(xué)生能提升數(shù)形結(jié)合，發(fā)展幾何直觀和空間想象能力；形成數(shù)學(xué)直觀，在具體的情境中感悟事物的本質(zhì).立體幾何是高中數(shù)學(xué)的重點(diǎn)，也是高考命題的熱點(diǎn)，分析歷年高考的立體幾何解答題，這就要求在課堂教學(xué)中要提升學(xué)生的直觀想象和邏輯推理的核心素養(yǎng).

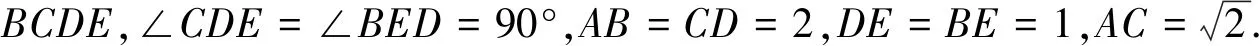
(Ⅰ)證明：DE⊥平面ACD；

(Ⅱ)求二面角B-AD-E的大小.

圖1

圖2

設(shè)平面ADE的法向量為m=(x1,y1,z1)，平面ABD的法向量為n=(x2,y2,z2)，

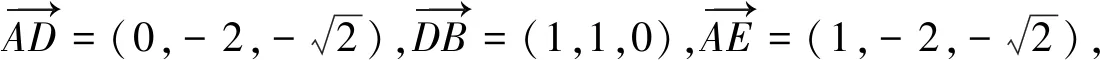
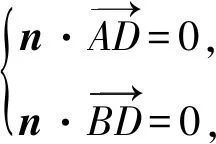
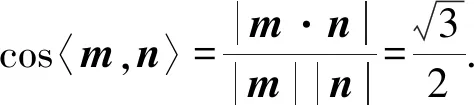
如果我們的課堂教學(xué)只關(guān)注學(xué)生能否解決此問(wèn)題和學(xué)生解題的速度和正確率，長(zhǎng)此以往，學(xué)生往往為了解題而解題，因?yàn)槭稚系念}目很多，要做的就是趕緊把題目都解答出來(lái).在這樣的壓力下，學(xué)生會(huì)按照最熟悉的路徑去執(zhí)行，用最熟練的方式去解決問(wèn)題——簡(jiǎn)而言之，就是路徑依賴.因?yàn)橹挥羞@樣，才能快速騰出手來(lái)，去做下一個(gè)題目.慢慢的，學(xué)生會(huì)開(kāi)始感覺(jué)到，沒(méi)有時(shí)間去深入思考.

這會(huì)導(dǎo)致學(xué)生在自己熟悉的領(lǐng)域，變得越來(lái)越熟練，但從來(lái)沒(méi)有真正突破原有的水平，只是成為了一個(gè)解題機(jī)器，并沒(méi)有提高素養(yǎng)，其視野很狹窄.只是在解題的時(shí)候，一味追求快速解題，讓自己像齒輪一樣跑起來(lái)，讓解題走在思維前面——經(jīng)過(guò)長(zhǎng)時(shí)間的強(qiáng)化，所固化下來(lái)的結(jié)果.

這種模式，本質(zhì)上，是無(wú)法真正提升核心素養(yǎng)的.因?yàn)閷W(xué)生只是一直在重復(fù)演練.在這種情況下，邊際效用是非常低的，這就是課堂效率低下的癥結(jié)所在.只有從多視角去看待問(wèn)題，思考解決此問(wèn)題的不同方法，講明用這種方法解決問(wèn)題的緣由，才能提高學(xué)生的核心素養(yǎng).

方法二(定義法)：作BF⊥AD，與AD交于點(diǎn)F，過(guò)點(diǎn)F作FG∥DE，與AE交于點(diǎn)G，連結(jié)BG，由(Ⅰ)知，DE⊥AD，則FG⊥AD，

圖3

所以∠BFG是二面角B-AD-E的平面角，在直角梯形BCDE中，由CD2=BD2+BC2，得BD⊥BC.

又平面ABC⊥平面BCDE，得BD⊥平面ABC，從而B(niǎo)D⊥AB.

圖4

圖5

方法四(三垂線法)：由(1)知BD⊥BC，所以BD⊥平面ABC.

所以平面ABD⊥平面ABC，取AB的中點(diǎn)M，所以CM⊥平面ABD.

延長(zhǎng)DE至F，使得DE=EF，則DC=DF.故點(diǎn)F與點(diǎn)C到平面ABD的距離相等.

圖6

方法五(面積射影法)：取DC的中點(diǎn)H，則BH⊥平面ADC，設(shè)二面角B-AD-C的平面角為θ，

方法六(三面角余弦定理)：

設(shè)α=∠BDE,β=∠ADB,γ=∠EDB，二面角B-AD-C的平面角為θ.

方法一(坐標(biāo)法)因?yàn)榇祟}有面面垂直的條件，由面面垂直的性質(zhì)定理可以做出面的垂線，故較易想到建立空間直角坐標(biāo)系，用坐標(biāo)法解決此問(wèn)題.方法二(定義法)分析構(gòu)成兩個(gè)半平面的幾何圖形的幾何特征，過(guò)公共棱上的一點(diǎn)在兩個(gè)半平面內(nèi)分別作出與公共棱垂直的直線，這樣就得到了二面角的平面角，此法就是用定義法作出二面角的平面角.方法三(三垂線法)用三垂線法作出二面角的平面角，先要找到其中一個(gè)平面的垂線，這樣就可以做出二面角的平面角.方法四(三垂線法)在法三的基礎(chǔ)上，利用“直線與平面相交，若平面兩側(cè)的斜線段長(zhǎng)相等，則垂線段長(zhǎng)相等”這一幾何直觀，不需要作出二面角的平面角，就能解決問(wèn)題，從而簡(jiǎn)化解題過(guò)程.方法五(面積射影法)與方法六(三面角余弦定理)為解決二面角的平面角提供了不同的解題思路.尤其在一些二面角的難題中，當(dāng)其他方法無(wú)效時(shí)，不妨用這兩種方法去嘗試一下.在選擇填空中，可以不作出二面角的平面角，就能較快地得到答案，起到事半功倍的效果.

我覺(jué)得立體幾何的教學(xué)中要遵循以下三原則：在直觀感知和操作確認(rèn)的基礎(chǔ)上建構(gòu)空間想象；在思辨論證和度量計(jì)算的基礎(chǔ)上培養(yǎng)邏輯推理；在深度學(xué)習(xí)和深度思考的基礎(chǔ)上提升核心素養(yǎng).

教師在教學(xué)中要有鉆研精神，遇到問(wèn)題不能淺嘗輒止，應(yīng)該考慮其他各種解法，解法是否具有通性通法，通過(guò)一題多解，幫助學(xué)生建構(gòu)起知識(shí)網(wǎng)絡(luò)，更好地掌握解決問(wèn)題的思路.教師在此過(guò)程中要引導(dǎo)學(xué)生分析不同解決思路的異同，通過(guò)一個(gè)問(wèn)題徹底理解一類問(wèn)題，讓學(xué)生在掌握基礎(chǔ)知識(shí)和基礎(chǔ)技能的同時(shí)，感悟基本思想方法，積累基本活動(dòng)經(jīng)驗(yàn)，提升和發(fā)展學(xué)生的數(shù)學(xué)核心素養(yǎng).