適應性回歸分析(Ⅳ)
——與非適應性回歸分析的比較

羅艷虹，胡良平

(1.山西醫科大學公共衛生學院衛生統計學教研室，山西 太原 030001；2.世界中醫藥學會聯合會臨床科研統計學專業委員會，北京 100029；3.軍事科學院研究生院，北京 100850

1 概 述

相對于因變量是“計數變量”和“定性變量”而言，因變量為“計量變量”的回歸建模方法的種類更多。其中，若按是否采用“適應性回歸分析”可劃分為以下兩類：適應性回歸分析[1-2]與非適應性回歸分析[3-12]。在非適應性回歸分析方法中，最常用且最有代表性的就是多重線性回歸分析方法，在SAS軟件中，可以通過REG過程來實現。

本文將采用ADAPTIVEREG過程和REG過程來實現對同一個數據集的回歸建模，并結合數據集和數據子集的真實情況，反映并揭示兩種建模思想對數據集和數據子集的建模效果。從而得出對回歸建模及建模效果評價有意義的參考性建議。

2 問題與數據結構

2.1 原問題與數據集

沿用本期科研設計方法專題中第二篇文章《適應性回歸分析(II)——排除噪聲變量的干擾》(以下簡稱“前文”)中的“問題與數據結構”，其數據集名為“artificial”。

2.2 新問題與數據集

在原問題中，數據集artificial包含一個因變量y及其取值，10個在(0，1)區間上服從均勻分布的隨機變量x1～x10及其取值；y是x1和x2的函數，并具有“前文”式(1)的表達式。整個數據集的樣本含量N=400。隨機變量x3～x10是獨立于因變量y的，或者說，它們是與因變量y無關的隨機變量。

2.3 擴展的數據集

2.3.1 擴展的數據集a1

在數據集artificial的基礎上，引入由隨機變量x1～x10產生的派生變量[3]，它們是由隨機變量x1～x10的全部二次項組成，共55項(包括10個平方項和45個交叉乘積項)。連同隨機變量x1～x10共有65個自變量，所得的數據集為a1。所需要的SAS數據步程序如下：

data a1;

set artificial;

z1=x1*x1;z2=x1*x2;z3=x1*x3;

z4=x1*x4;z5=x1*x5;z6=x1*x6;

z7=x1*x7;z8=x1*x8;z9=x1*x9;

z10=x1*x10;z11=x2*x2;z12=x2*x3;

z13=x2*x4;z14=x2*x5;z15=x2*x6;

z16=x2*x7;z17=x2*x8;z18=x2*x9;

z19=x2*x10;z20=x3*x3;z21=x3*x4;

z22=x3*x5;z23=x3*x6;z24=x3*x7;

z25=x3*x8;z26=x3*x9;z27=x3*x10;

z28=x4*x4;z29=x4*x5;z30=x4*x6;

z31=x4*x7;z32=x4*x8;z33=x4*x9;

z34=x4*x10;z35=x5*x5;z36=x5*x6;

z37=x5*x7;z38=x5*x8;z39=x5*x9;

z40=x5*x10;z41=x6*x6;z42=x6*x7;

z43=x6*x8;z44=x6*x9;z45=x6*x10;

z46=x7*x7;z47=x7*x8;z48=x7*x9;

z49=x7*x10;z50=x8*x8;z51=x8*x9;

z52=x8*x10;z53=x9*x9;z54=x9*x10;

z55=x10*x10;

run;

【說明】在上面的程序中，“z1=x1*x1”和“z11=x2*x2”分別代表x1與x2的平方項；“z2=x1*x2”代表x1與x2的交叉乘積項；z3～z10代表與x1有關的交叉乘積項；z12～z19代表與x2有關的交叉乘積項。也就是說，z1～z19或多或少與因變量y有一定的聯系。z20～z55這36個變量都獨立于因變量y；另外，由前面的介紹可知，隨機變量x3～x10是獨立于因變量y的，故獨立于因變量y的自變量共有44個(即x1～x10，z20～z55)。

2.3.2 擴展的數據集a2

由于因變量y是計量變量，故可以對其進行變量變換。常規的變量變換方法有以下五種：對數變換、平方根變換、倒數變換、指數變換和Logistic變換[13-15]。在數據集a1基礎上，引入對因變量y的上述五種變換，分別記為y1～y5，所得的數據集為a2。所需要的SAS數據步程序如下：

data a2;

set a1;

y1=log(y+5);y2=sqrt(y+5);y3=1/(y+5);

y4=exp(y+5);y5=exp(y+5)/(1+exp(y+5));

run;

【說明】因為在因變量y的取值中，出現了負數和零，不便于取對數和平方根變換，統一加上一個正數5即可。

數據集a2中包含了數據集a1，而其又包含了數據集artificial，故以下僅基于數據集a2進行計算即可。

2.3.3 數據集a2中變量的分類

因變量有6種表現形式，分別為原先的形式y、取了不同變量變換后的形式y1～y5；自變量可分為以下兩類：A類中含有21個與因變量有關系的自變量，即“x1和x2，z1～z19”；B類中含有44個與因變量無關系的自變量，即“x3～x10，z20～z55”。

3 基于a2數據集中A與B兩類共65個自變量進行回歸建模

3.1 采用ADAPTIVEREG過程對65個自變量進行回歸建模

3.1.1建模策略

分別選取y、y1～y5為因變量，利用65個自變量(其中，A類21個自變量與因變量有關系，B類44個自變量與因變量無關系)，采用ADAPTIVEREG過程進行回歸建模。

3.1.2 建模結果

建模的輸出結果較多，下面僅給出自變量對因變量貢獻排名前五位的自變量及反映其重要性大小的百分數。見表1。

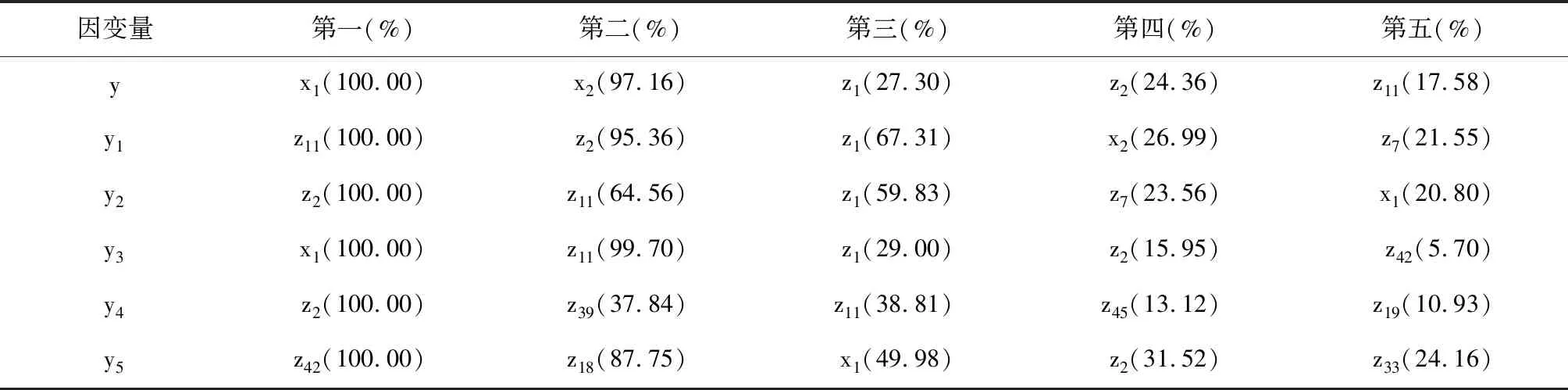
表1 ADAPTIVEREG過程對65個自變量進行回歸建模給出前五位自變量及其重要性數值

由表1可知：分別以“y、y1和y2”為因變量時，ADAPTIVEREG過程從65個自變量中提取的前五位重要的自變量全部屬于A類中的自變量；而分別以“y3、y4和y5”為因變量時，ADAPTIVEREG過程從65個自變量中提取的前五位重要的自變量中分別有4、3、3個屬于A類中的自變量，即出錯數目分別為1、2、2個。

3.2 采用REG過程對65個自變量進行回歸建模

3.2.1建模策略

分別選取y、y1～y5為因變量，利用65個自變量(其中，A類21個自變量與因變量有關系，B類44個自變量與因變量無關系)，采用REG過程進行回歸建模。具體地說，在假定模型包含截距項與不含截距項的條件下，再分別采用“前進法”“后退法”和“逐步法”篩選自變量，并記錄下最終回歸模型的有關重要信息。

3.2.2 建模結果

建模的輸出結果較多，下面僅給出最終的回歸模型中分別包含A類與B類自變量的數目。見表2。

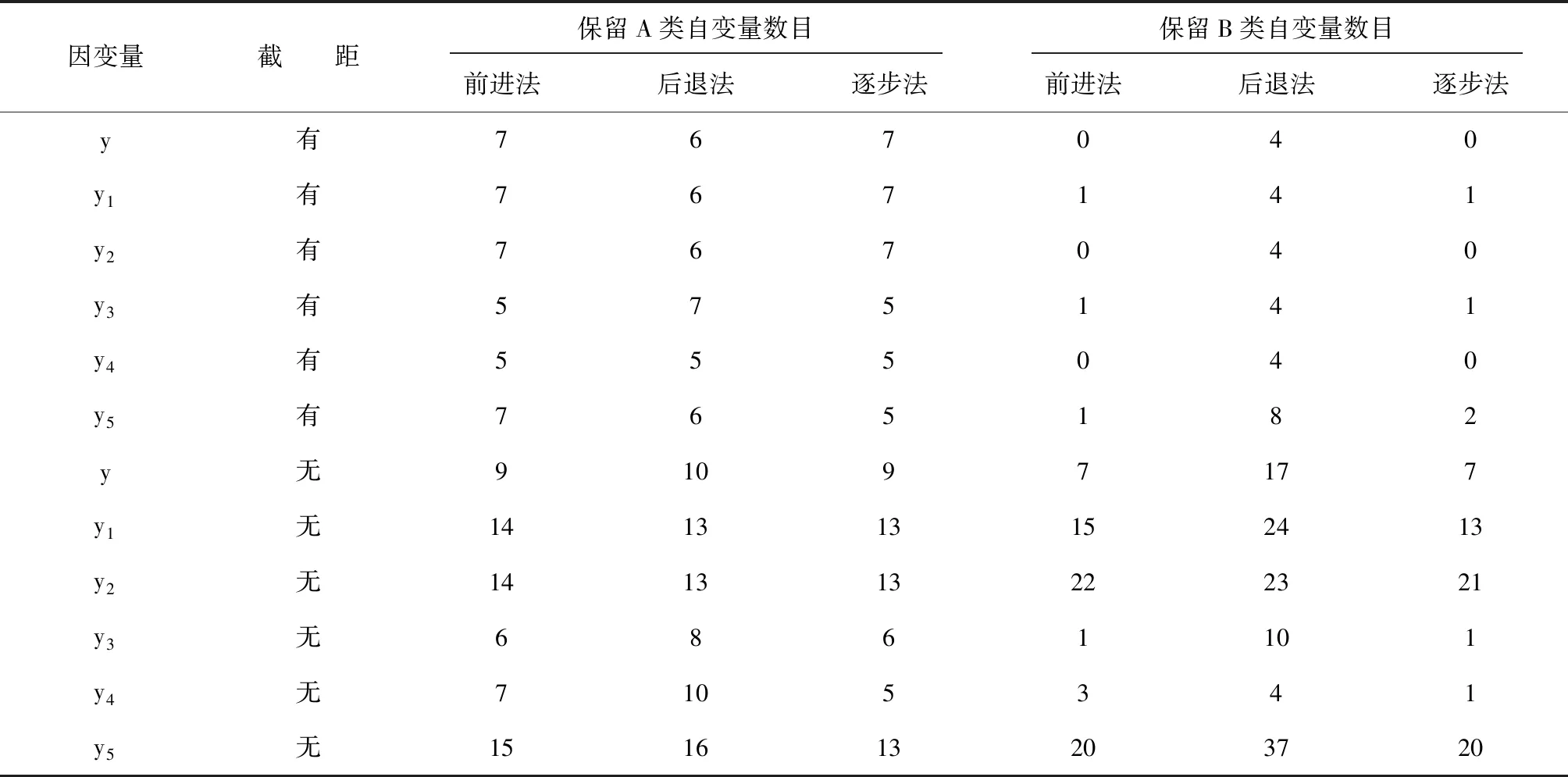
表2 REG過程對65個自變量進行回歸建模保留A與B類自變量的數目

由表2可知：假定回歸模型中不含截距項時，保留在回歸模型中的自變量數目明顯增多，此時，有很多與因變量無關的自變量會被保留在最終的回歸模型之中。假定回歸模型中包含截距項且采用前進法或逐步法篩選自變量時，回歸模型中保留與因變量無關的自變量的數目比較少，即結論的正確性較高。

4 基于a2數據集的B類中44個自變量進行回歸建模

4.1 采用ADAPTIVEREG過程對B類中44個自變量進行回歸建模

4.1.1建模策略

分別選取y、y1～y5為因變量，利用B類中44個自變量，采用ADAPTIVEREG過程進行回歸建模。

4.1.2 建模結果

建模的輸出結果很多，為節省篇幅，下面僅給出自變量對因變量貢獻排名前五位的自變量及反映其重要性大小的百分數。見表3。由表3可知：盡管B類中44個自變量獨立于因變量，但ADAPTIVEREG過程仍以較高的“重要性”數值保留了較多的自變量。

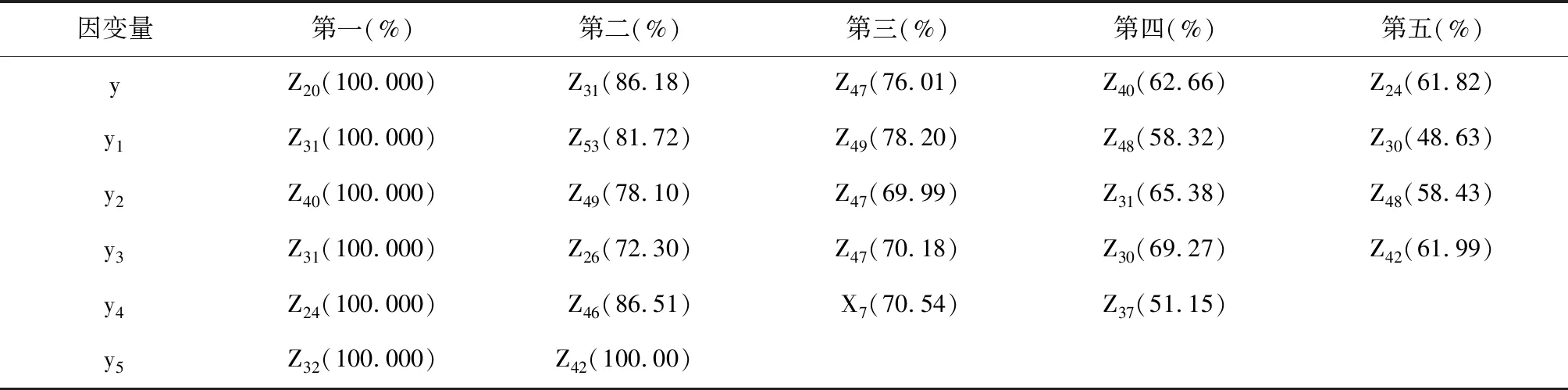
表3 ADAPTIVEREG過程對B類中44個自變量進行回歸建模給出前五位自變量及其重要性數值

4.2 采用REG過程對B類中44個自變量進行回歸建模

4.2.1 建模策略

分別選取y、y1～y5為因變量，利用B類中44個自變量，采用REG過程進行回歸建模。具體地說，在假定模型包含截距項與不含截距項的條件下，再分別采用“前進法”“后退法”和“逐步法”篩選自變量，并記錄下最終回歸模型的有關重要信息。

4.2.2 建模結果

建模的輸出結果較多，下面僅給出最終的回歸模型中包含B類自變量的數目。見表4。

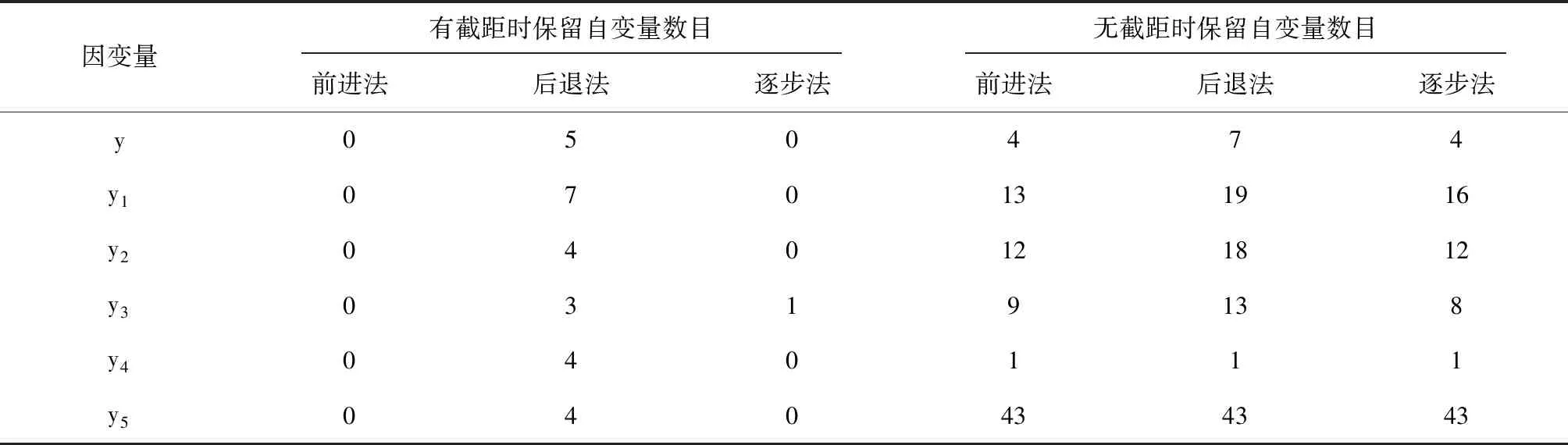
表4 REG過程對B類中44個自變量進行回歸建模保留自變量的數目

由表4可知：假定回歸模型中包含截距項且采用前進法篩選自變量時，與因變量無關的自變量全部都不被保留在回歸模型中，結果最可信；假定回歸模型中包含截距項且采用逐步法篩選自變量時，與因變量無關的自變量幾乎都不被保留在回歸模型中(本例僅因變量y3時有一個自變量)，結果比較可信；而假定回歸模型中不含截距項且采用“指數變換(因變量y4)”時，與因變量無關的自變量被保留在回歸模型中的數目最少(本例中出現了一個)；假定回歸模型中不含截距項且采用Logistic變換(因變量y5)時，與因變量無關的自變量被保留在回歸模型中的數目最多(本例中出現了43個)。

5 回歸建模所需要的SAS程序

5.1 實現表1和表3計算的SAS程序

5.1.1 實現表1計算所需要的SAS過程步程序

proc adaptivereg data=a2;

model y=x1-x10 z1-z55;

quit;

5.1.2 實現表3計算所需要的SAS過程步程序

proc adaptivereg data=a2;

model y=x3-x10z20-z55;

quit;

5.1.3 關于上述SAS程序的說明

將因變量y依次修改為“y1～y5”，分別運行上面的SAS過程步程序。

5.2 實現表2和表4計算的SAS程序

5.2.1 實現表2計算所需要的SAS過程步程序

proc reg data=a2;

model y=x1-x10 z1-z55/selection=forward sle=0.05;

quit;

proc reg data=a2;

model y=x1-x10 z1-z55/noint selection=forward sle=0.05;

quit;

5.2.2 實現表4計算所需要的SAS過程步程序

proc reg data=a2;

model y= x3-x10 z20-z55/selection=forward sle=0.05;

quit;

proc reg data=a2;

model y=x3-x10 z20-z55/noint selection=forward sle=0.05;

quit;

5.2.3 關于上述SAS程序的說明

將“model語句”中的“selection=”及其后面的內容分別修改為“backward sls=0.05;”和“stepwise sle=0.5 sls=0.05;”，就是采用“后退法”和“逐步法”篩選自變量；將因變量y依次修改為“y1～y5”，分別運行上面的SAS過程步程序。

6 討論與結論

6.1 討論

統計學教科書上所講授的、統計軟件中所實現的回歸分析方法，主要依據是數學原理和數理統計知識；實際工作者在運用回歸分析技術時，并不知曉資料的自變量中哪些與因變量有關系、哪些與因變量無關系，全依靠回歸分析技術和統計軟件計算的結果來作出肯定或否定的結論。

基于本文的“數據結構”“真實情況”和“兩種回歸建模思路及計算結果”，可提出以下問題：在通常情況下，使用回歸分析技術處理各種“真實情況未知”的試驗數據時，所得到的“回歸分析結果”的可信度究竟有多高？究竟應該如何提高回歸分析結果的可信度？

筆者認為：對于“真實情況未知”的試驗數據而言，無論采用“參數法”“半參數法”“非參數數”或所謂的“機器學習或深度學習”等方法進行回歸建模，都是在“無中生有”，其整個過程都是一個“黑箱”，結果的可信度在相當大的程度上取決于資料中變量之間的真實情況。然而，當研究者對資料的真實情況一無所知時，應采取非常審慎的態度看待其分析結果。

6.2 結論

當資料中存在與因變量確有關系的自變量時，①由表1可知，ADAPTIVEREG過程具有較好的甄別能力；當對因變量采取對數變換或平方根變換時，其甄別能力下降；當對因變量采取倒數變換或指數變換或Logistic變換時，其甄別能力下降較為明顯。②由表2可知，REG過程具有較好的甄別能力，但需要滿足一定條件，即采用“前進法”或“逐步法”篩選自變量，同時還需要“假定模型包含截距項”。

當資料中不存在與因變量確有關系的自變量時，①由表3可知，ADAPTIVEREG過程幾乎完全失去了甄別能力；②由表4可知，REG過程具有較好的甄別能力，但需要滿足一定條件，即采用“前進法”篩選自變量，同時還需要“假定模型包含截距項”。若對因變量采取指數變換且“假定模型不含截距項”時，無論采取“前進法”“后退法”或“逐步法”篩選自變量，都具有較好的甄別能力(見表4中倒數第2行最后3個數據，從44個獨立于因變量的自變量中僅錯誤地保留了一個自變量)。若研究者基于基本常識和專業知識確定的自變量都與因變量有關系，對因變量進行Logistic變換，并且，假定回歸模型中不含截距項時，會在回歸模型中保留非常多的自變量。此時，反映模型對資料擬合效果的R2值非常接近1、均方誤差MSE的數值遠遠小于1(因輸出結果較多，未在表2和表4中呈現出來)。