適應性回歸分析(Ⅲ)構建具有混合結構的回歸模型
——

羅艷虹，胡良平

(1.山西醫科大學公共衛生學院衛生統計學教研室，山西 太原 030001；2.世界中醫藥學會聯合會臨床科研統計學專業委員會，北京 100029；3.軍事科學院研究生院，北京 100850

1 基于多個回歸模型采用ADAPTIVEREG過程實現一次性擬合

1.1 問題與模型

【實例1】假定在自變量的定義域內，可以構造出三個回歸模型，它們分別為指數回歸模型、對數回歸模型和直線回歸模型[1-2]。這三個回歸模型的表達式見式(1)。

(1)

是否可以通過一個SAS過程步來一次性擬合出上述三個回歸模型？

1.2 利用ADAPTIVEREG過程實現上述要求

1.2.1 所需要的SAS程序

data Mixture;

drop i;

do i=1 to 1000;

X=ranuni(1);

C=int(3*ranuni(1));

if C=0 then Y=exp(5*(X-0.3)**2)+rannor(1);

else if C=1 then Y=log(X*(1-X))+rannor(1);

else Y=7*X+rannor(1);

output;

end;

run;

ods graphics on;

proc adaptivereg data=Mixture plots=fit;

class c;

model y=c x;

run;

1.2.2 SAS數據步程序說明

在SAS數據步程序中，擬產生1 000個觀測(即樣本含量N=1 000)；將自變量X設置為在“0～1”區間上變化且服從均勻分布的隨機變量；首先將分類變量C設置為在“0～1”區間上變化且服從均勻分布的隨機變量，然后將變量C乘以3，最后再將其取整(這樣做的目的是使“C”成為隨機變量，而不是一般變量，也就是說，它在數據集中的取值仍為0～2，但不是按確定性的順序出現的，而是隨機出現的)；接下來按式(1)進行計算，得出C在取不同值條件下的因變量y的數值。應注意：在因變量y的每個數值上，還加上了一個服從N(0,1)分布的隨機變量的數值，其意義在于：因變量y也是一個隨機變量，而不是一個一般變量。

1.2.3 SAS過程步程序說明

調用“ADAPTIVEREG過程”，在過程步語句中，要求繪制圖形；使用“CLASS語句”，指定分類變量為“C”；在“MODEL語句”中，包含了兩個自變量，一個為變量C、另一個為變量X。

1.2.4 SAS主要輸出結果及解釋

擬合統計量GCV1.08046GCV R-Square0.90279Effective Degrees of Freedom25R-Square0.90740Adjusted R-Square0.90628Mean Square Error1.04064Average Square Error1.02711

以上為擬合統計量的計算結果，R2和調整R2分別為0.90740和0.90628，說明模型對資料的擬合效果比較好。

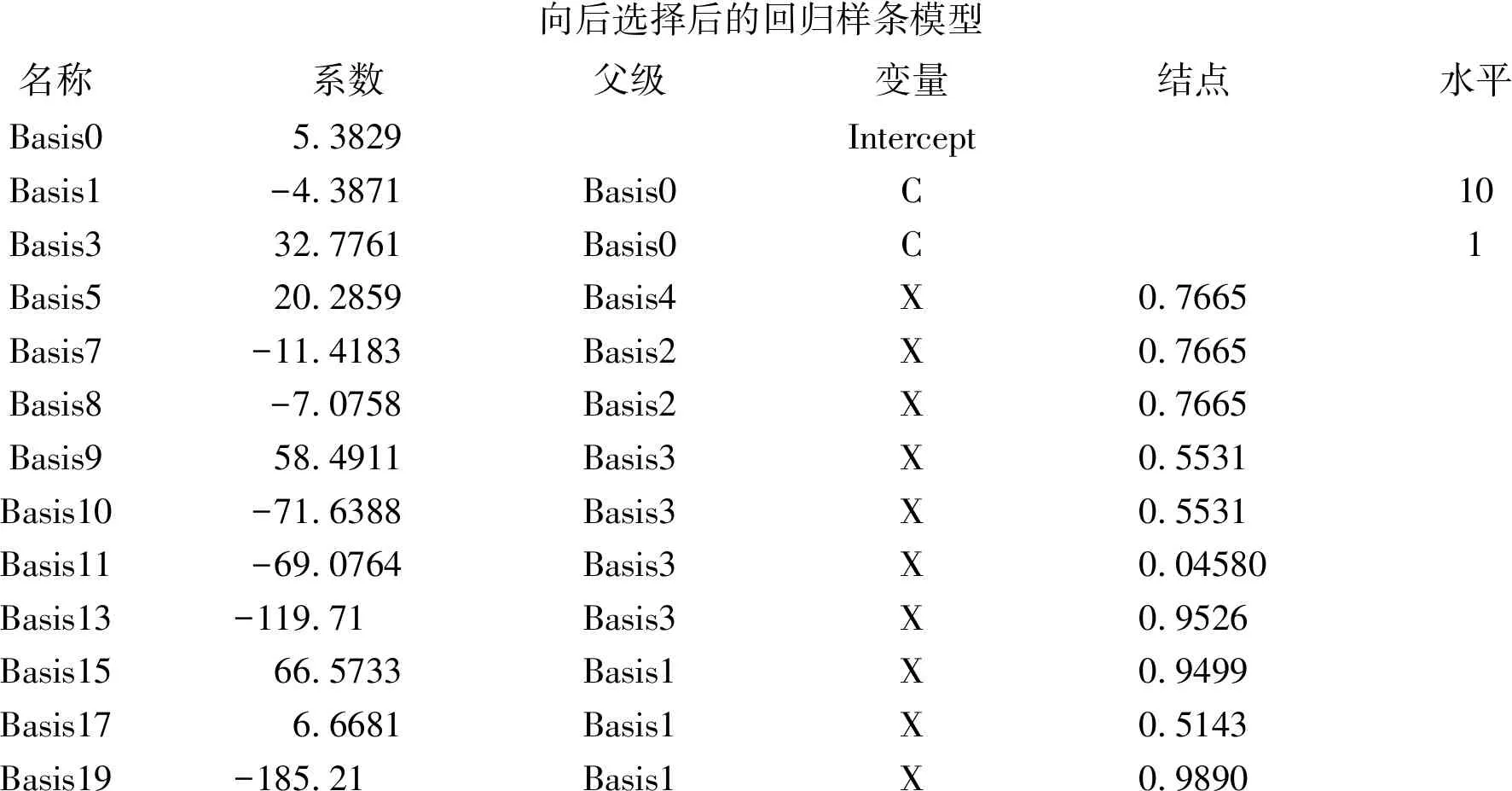
向后選擇后的回歸樣條模型名稱系數父級變量結點水平Basis05.3829InterceptBasis1-4.3871Basis0C10Basis332.7761Basis0C1Basis520.2859Basis4X0.7665Basis7-11.4183Basis2X0.7665Basis8-7.0758Basis2X0.7665Basis958.4911Basis3X0.5531Basis10-71.6388Basis3X0.5531Basis11-69.0764Basis3X0.04580Basis13-119.71Basis3X0.9526Basis1566.5733Basis1X0.9499Basis176.6681Basis1X0.5143Basis19-185.21Basis1X0.9890

以上為“向后選擇后的回歸樣條模型”中“各基函數”及其回歸系數，以“基函數”為新“自變量”的適應性回歸模型比式(1)更復雜。

ANOVA分解功能性成分基數DF變化量(若忽略)失擬GCVC241112.501.1519C X10203773.943.7690

以上為“方差分析分解”的計算結果，對因變量y影響較大的是“C”與“X”之間的交互作用項，其次是變量C。

變量重要性 變量基數重要性C12100.00X1050.68

以上為兩個變量“C”與“X”對因變量y的重要性的計算結果，可以看出：變量C對因變量y的影響最大，其次是變量X。

擬合結果用圖示法呈現，見圖1。

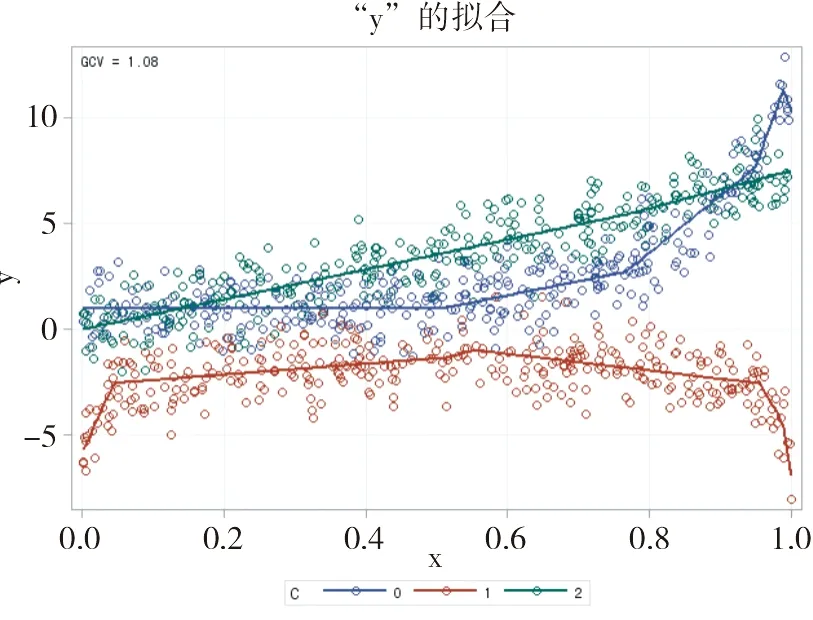
圖1 ADAPTIVEREG過程按式(1)擬合的結果

由圖1可知：自上而下有三條線，第1條為“直線”，對應式(1)中第3式；第2條為“指數曲線”，對應式(1)中第1式；第3條為“對數曲線”，對應式(1)中第2式。

2 基于具有混合結構的數據集采用ADAPTIVEREG過程實現一次性擬合

2.1 問題與數據結構

【實例2】假定有一個具有混合結構的數據集。見表1。

在此次研究中,觀察組患者的腹脹幾率是5.46%,對照組的腹脹幾率是21.82%,兩組結果對比存在統計學差異性(P<0.05)。觀察組患者的胃腸蠕動時間、腸鳴音、肛門排氣時間等均比對照組短,兩組結果存在統計學差異性(P<0.05)。觀察組臨床護理滿意度是94.54%,對照組是76.37%,結果存在統計學差異性(P<0.05)。

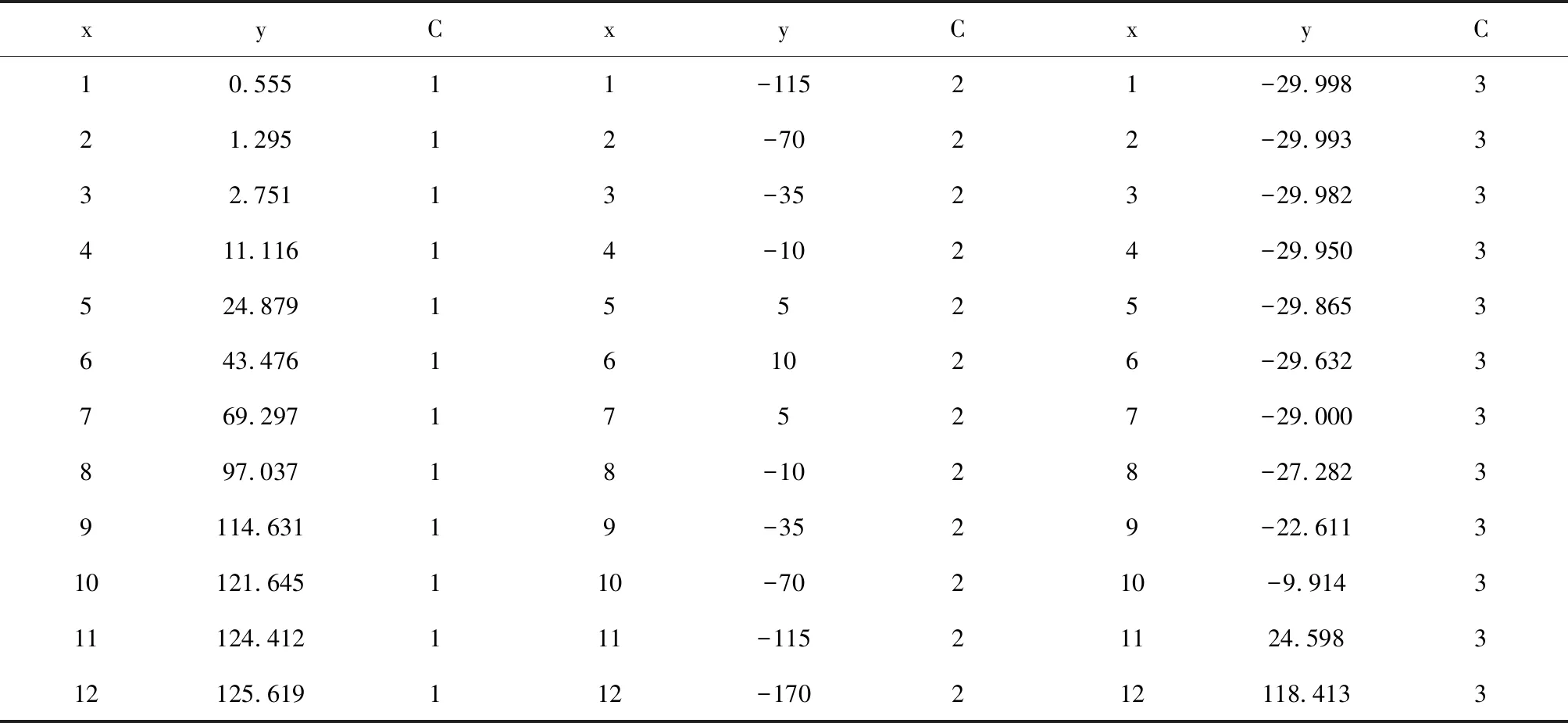
表1 一個具有三類(C=1、2、3)結構不同的混合型數據集

注：在C=1、2、3類的數據集中，x的取值均為1～12，但y的取值是不同的

【問題】試在每一類中，構建y依賴x變化而變化的回歸模型。

2.2 試采用ADAPTIVEREG過程直接擬合該數據集

2.2.1 創建SAS數據集

所需要的SAS數據步程序如下：

Data a1;

INPUT x y c @@;

CARDS;

此處輸入表1中12行6列數據;

;

RUN;

所需要的SAS過程步程序如下：

ods graphics on;

proc adaptivereg data=a1 plots=fit;

class c;

model y=c x;

run;

2.2.3 顯示SAS主要分析結果

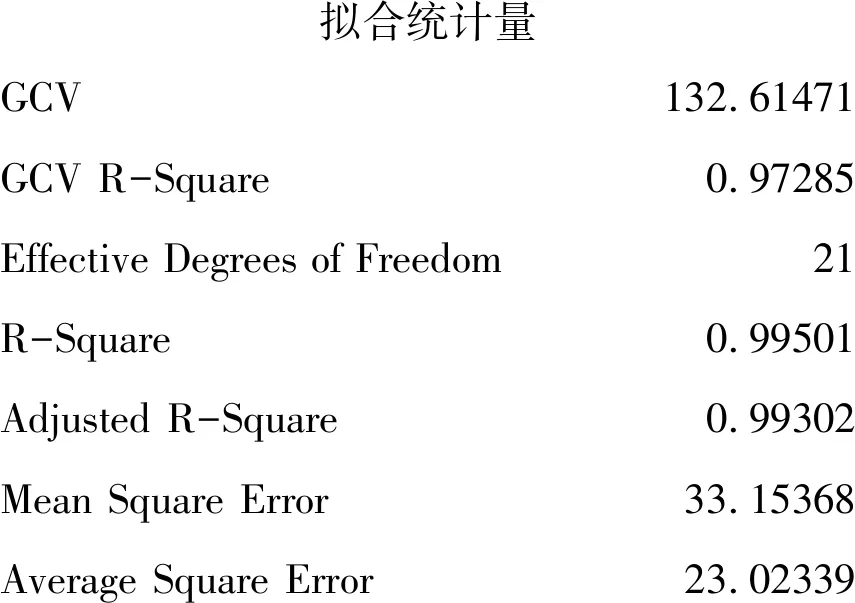
擬合統計量GCV132.61471GCV R-Square0.97285Effective Degrees of Freedom21 R-Square0.99501 Adjusted R-Square0.99302 Mean Square Error33.15368 Average Square Error23.02339

以上為“擬合統計量”的計算結果。由R2和調整R2的計算結果可知，模型對資料的擬合效果比較好。

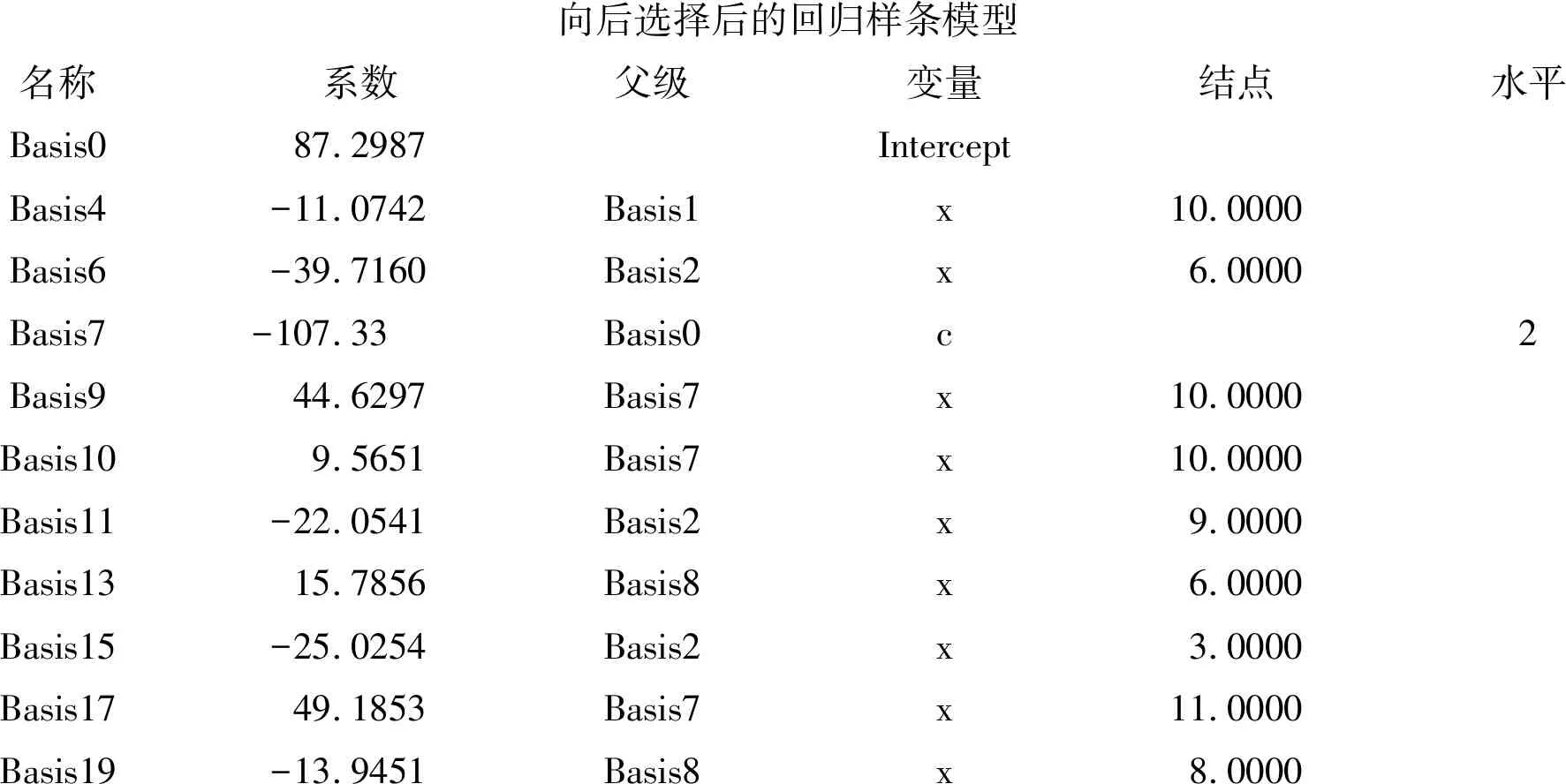
向后選擇后的回歸樣條模型名稱系數父級變量結點水平Basis087.2987InterceptBasis4-11.0742Basis1x10.0000Basis6-39.7160Basis2x6.0000Basis7-107.33Basis0c2Basis944.6297Basis7x10.0000Basis109.5651Basis7x10.0000Basis11-22.0541Basis2x9.0000Basis1315.7856Basis8x6.0000Basis15-25.0254Basis2x3.0000Basis1749.1853Basis7x11.0000Basis19-13.9451Basis8x8.0000

以上為“向后選擇后的回歸樣條模型”的計算結果，需要用到19個“基函數”。

ANOVA分解功能性成分基數DF變化量(若忽略)失擬GCVC12128071565.97C X9181633895296.08

以上為“方差分析分解”的計算結果，說明變量C和“C”與“X”的交互作用項對因變量y的影響很大。

變量重要性變量基數重要性C9100.00X1093.90

以上是對兩個變量的重要性所做的評價，兩個變量對于因變量y的影響都很大。

由于模型的表達式非常復雜且不直觀，SAS采用圖形方式呈現模型擬合結果。見圖2。

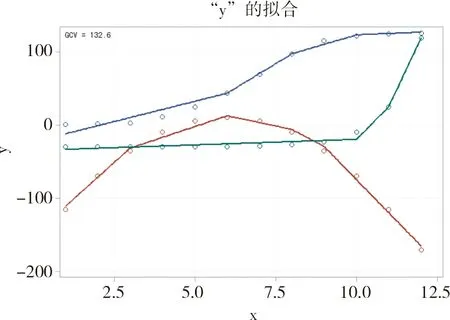
圖2 采用ADAPTIVEREG過程擬合表1資料的結果以圖形呈現

在圖2中，可以比較清楚地看出：在“C=1”類中，y與x之間呈現“Logistic曲線”關系；在“C=2”類中，y與x之間呈現“拋物線”關系；在“C=3”類中，y與x之間呈現“指數曲線”關系。

2.3 數據結構的揭秘

在表1的“C=1”類中，(x，y)的兩列數據來自文獻[3]，該資料描述的是“某縣瘧疾發病的季節性特點”，即某縣1961年-1996年瘧疾的月累計發病率(x代表1月-12月，y代表“累計發病率”，單位為“1/10萬”)。繪制該資料的散布圖，呈現“Logistic曲線”變化趨勢，適合擬合“Logistic曲線回歸模型”。

在表1的“C=2”類中，(x，y)的兩列數據中的“x”保持不變，而“y”列數據是采用如下的式(2)計算出來的：

y=-5×(x-6)2+10

(2)

式(2)表達的是一個y關于x 的“二次拋物線模型”。

在表1的“C=3”類中，(x，y)的兩列數據中的“x”保持不變，而“y”列數據是采用如下的式(3)計算出來的：

y=e(x-7)-30

(3)

式(3)表達的是一個y關于x 的“指數曲線模型”。

結合上面圖1中呈現的“三條曲線”及其解釋，不難發現：適應性回歸樣條算法給出的結果與數據所代表的真實模型是基本吻合的。

3 討論與結論

3.1 討論

“實例1”與“實例2”看起來有所不同，前者似乎是從“模型”出發，產生“數據”，再用“ADAPTIVEREG過程”去擬合數據；而后者似乎是從“數據”出發，采用“ADAPTIVEREG過程”去擬合數據，再交代各類數據所代表的“模型”。其實，二者在本質上是完全一樣的。對于“ADAPTIVEREG過程”而言，它并不知曉正在擬合的“數據”究竟包含了“哪幾種模型”或存在“哪些客觀規律”，只是基于“特定類中兩變量之間的數量關系”并依據“適應性回歸樣條算法”去逐一構造“基函數”，在“失擬(LOF)”和“廣義交叉驗證(GCV)”等的“擬合優度評價指標”的“監控”之下，找到“基函數”及其組合。

3.2 結論

適應性回歸樣條算法(由ADAPTIVEREG過程實現)確實具有一定的揭示“混雜結構數據集”中隱藏的數據規律的“能力”；然而，它給出的基于“基函數”的“回歸模型”過于復雜且很不直觀；通過“圖形方式”呈現的結果雖然很直觀，但很不“精確”，不同的分析者可能會給出不同的“解讀結果”。但是，圖形呈現的結果確實可以給分析者提供一些有價值的“分析線索”或“積極暗示”，有利于分析者縮小“探索性研究的空間”[4]。