適應性回歸分析(Ⅱ)
——排除噪聲變量的干擾

羅艷虹，胡良平

(1.山西醫科大學公共衛生學院衛生統計學教研室，山西 太原 030001；2.世界中醫藥學會聯合會臨床科研統計學專業委員會，北京 100029；3.軍事科學院研究生院，北京 100850

1 一個人工生成的數據集

1.1 生成數據的構想

生成包含一個因變量和10個連續型自變量的模擬數據集，樣本含量N=400。生成的方法如下：

第一，每個連續型自變量都是從一個均勻分布總體U(0，1)中獨立抽樣產生的，它們分別被命名為x1～x10。

第二，因變量y僅由兩個連續型自變量x1和x2按式(1)計算而得到：

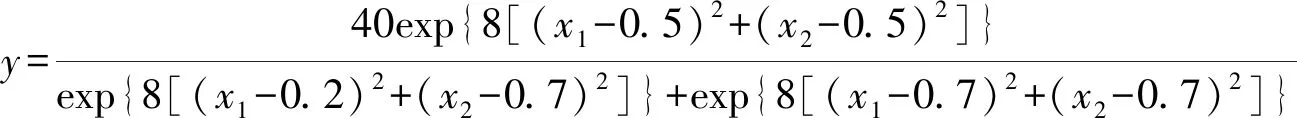
(1)

在給定了連續型自變量x1和x2的每一對數值后，將它們代入式(1)，并且，基于標準正態分布N(0，1)添加誤差而生成真實模型。把樣本含量設定為N=400[1]。

1.2 用SAS生成上述數據的方法

1.2.1生成包含11個變量及其400個觀測值所需要的SAS程序

data artificial;

drop i;

array x{10};

do i=1 to 400;

do j=1 to 10;

x{j} = ranuni(1);

end;

y=40*exp(8*((x1-0.5)**2+(x2-0.5)**2))/

exp(8*((x1-0.2)**2+(x2-0.7)**2))+

exp(8*((x1-0.7)**2+(x2-0.2)**2)))+rannor(1);

output;

end;

run;

1.2.2輸出數據集前10個觀測所需要的SAS程序

proc print data=artificial(obs=10);

var x1-x10 y;

run;

1.2.3 輸出數據集前10個觀測

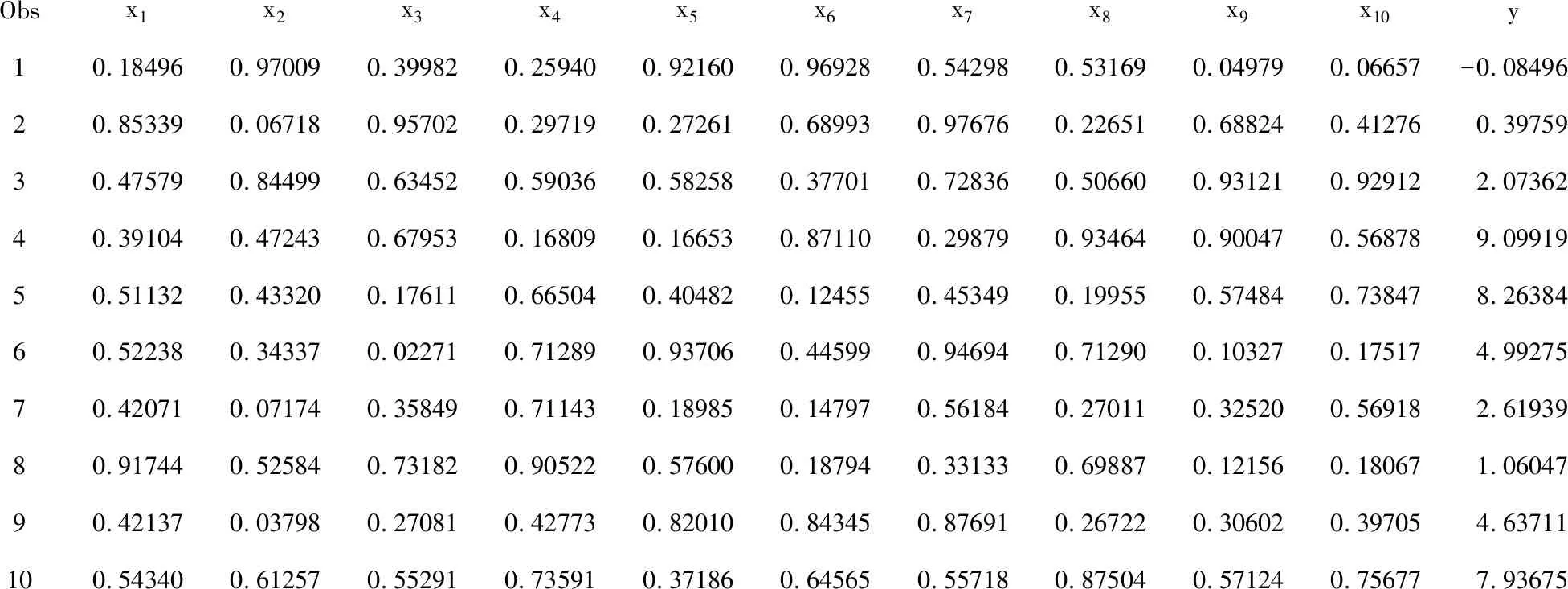
Obsx1x2x3x4x5x6x7x8x9x10y10.184960.970090.399820.259400.921600.969280.542980.531690.049790.06657-0.0849620.853390.067180.957020.297190.272610.689930.976760.226510.688240.412760.3975930.475790.844990.634520.590360.582580.377010.728360.506600.931210.929122.0736240.391040.472430.679530.168090.166530.871100.298790.934640.900470.568789.0991950.511320.433200.176110.665040.404820.124550.453490.199550.574840.738478.2638460.522380.343370.022710.712890.937060.445990.946940.712900.103270.175174.9927570.420710.071740.358490.711430.189850.147970.561840.270110.325200.569182.6193980.917440.525840.731820.905220.576000.187940.331330.698870.121560.180671.0604790.421370.037980.270810.427730.820100.843450.876910.267220.306020.397054.63711100.543400.612570.552910.735910.371860.645650.557180.875040.571240.756777.93675

1.3 數據結構的特點

x1～x10都是在“0～1”之間取值且服從均勻分布的隨機變量，它們之間是互相獨立的；y是在依據式(1)計算結果的基礎上，添加一個服從“均值為0、方差為1”的標準正態分布隨機變量的取值(或稱為誤差)。顯然，11個變量都是計量的，且y僅依賴于x1和x2兩個變量，獨立于“x3～x10”這8個變量。

1.4 回歸分析的目的

【實例1】 基于前述的數據集，試建立y依賴于x1～x10的多重回歸模型。

【實例2】 基于前述的數據集，試建立y依賴于x1和x1～x10的多重回歸模型(即丟棄x2)。

【實例3】 基于前述的數據集，試建立y依賴于x2～x10的多重回歸模型(即丟棄x1)。

【實例4】 基于前述的數據集，試建立y依賴于x3～x10的多重回歸模型(即丟棄x1和x2)。

2 利用ADAPTIVEREG過程建模[1-2]

2.1 對實例1進行適應性回歸分析

2.1.1 所需要的SAS過程步程序

ods graphics on;

proc adaptivereg data=artificial plots=fit;

model y=x1-x10;

run;

2.1.2 SAS輸出結果及解釋

擬合統計量GCV1.55656GCV R-Square0.86166Effective Degrees of Freedom27R-Square0.87910Adjusted R-Square0.87503Mean Square Error1.40260Average Square Error1.35351

以上為“擬合統計量”的計算結果，模型對資料的擬合優度界值GCV=1.55656；R2和調整R2分別為0.87910和0.87503；均方誤差和平均平方誤差分別為1.40260和1.35351。

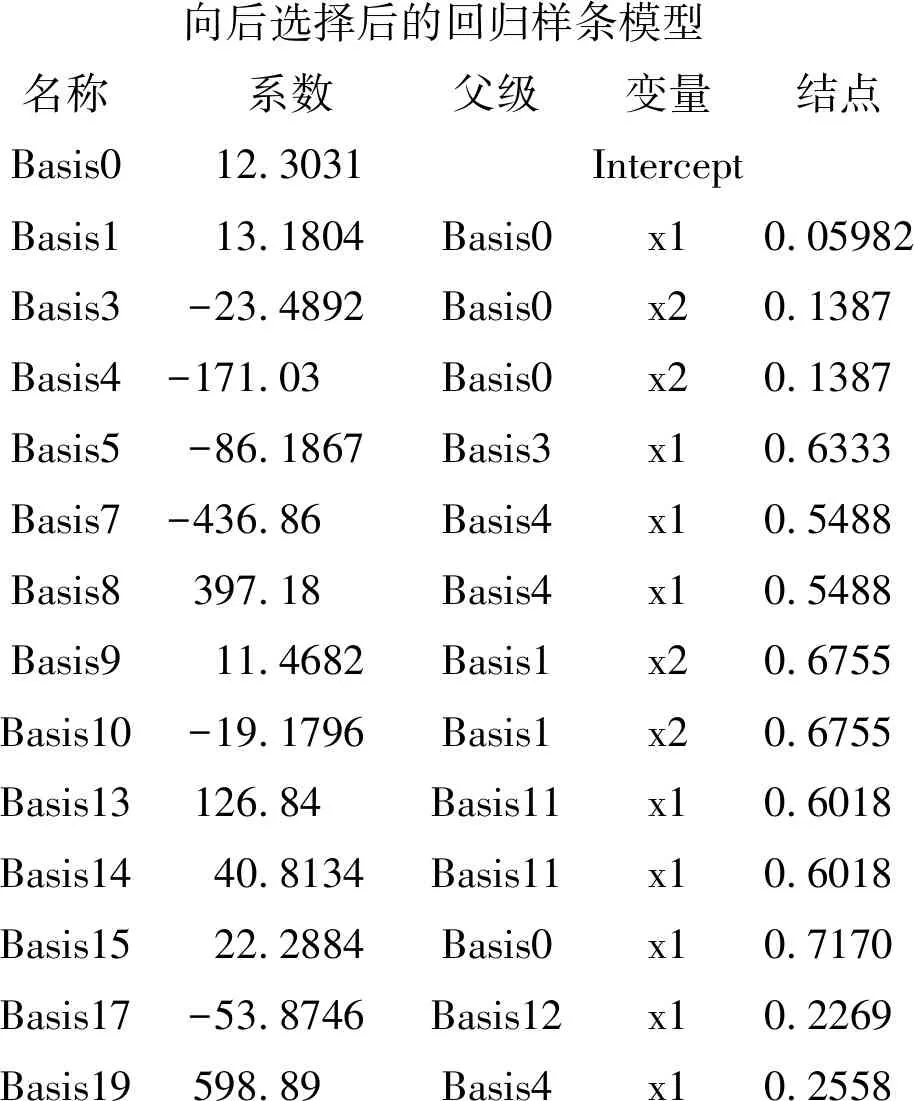
向后選擇后的回歸樣條模型名稱系數父級變量結點Basis012.3031InterceptBasis113.1804Basis0x10.05982Basis3-23.4892Basis0x20.1387Basis4-171.03Basis0x20.1387Basis5-86.1867Basis3x10.6333Basis7-436.86Basis4x10.5488Basis8397.18Basis4x10.5488Basis911.4682Basis1x20.6755Basis10-19.1796Basis1x20.6755Basis13126.84Basis11x10.6018Basis1440.8134Basis11x10.6018Basis1522.2884Basis0x10.7170Basis17-53.8746Basis12x10.2269Basis19598.89Basis4x10.2558

以上為“向后選擇后的回歸樣條模型”的計算結果。此結果中涉及到很多“基函數(Basis)”，而基函數中的“元素”基本上只有“x1”“x2”以及由它們以不同的系數聯系起來的“交互作用項”。

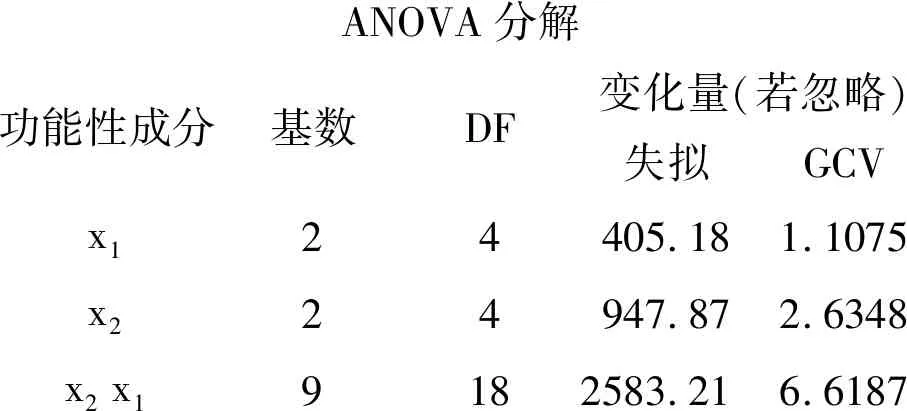
ANOVA分解功能性成分基數DF變化量(若忽略)失擬GCVx124405.181.1075x224947.872.6348x2 x19182583.216.6187

以上是基于“方差分析分解”的算法對所構建的模型進行逐項分解的結果。其中，涉及到“x1”的基函數有2個，占用了4個自由度，其對應的“失擬”LOF=405.18，GCV=1.1075；涉及到“x2”的基函數有2個，占用了4個自由度，其對應的LOF=947.87，GCV=2.6348；涉及到“x1”與“x2”交互作用項的基函數有9個，占用了18個自由度，其對應的LOF=2583.21，GCV=6.6187。

【說明】在上面的輸出結果中，最后兩列的頂端“變化量(若忽略)”，其含義是：若忽略掉各行上的“項”(第1行為“x1”、第2行為“x2”、第3行為“x1×x2”)，將會使“失擬(LOF)”或“廣義交叉驗證(GCV)”發生改變的數量大小，此“變化量”越大，表明對應行上的“項”對因變量的影響越大。

變量重要性變量基數重要性x111100.00x21199.19

以上結果表明：x1與x2對因變量y的重要性接近相等，分別為100.00%、99.19%。

因變量y關于x1與x2的二次曲面回歸模型在二維直角坐標系內以“等高線”呈現出來的圖形見圖1。

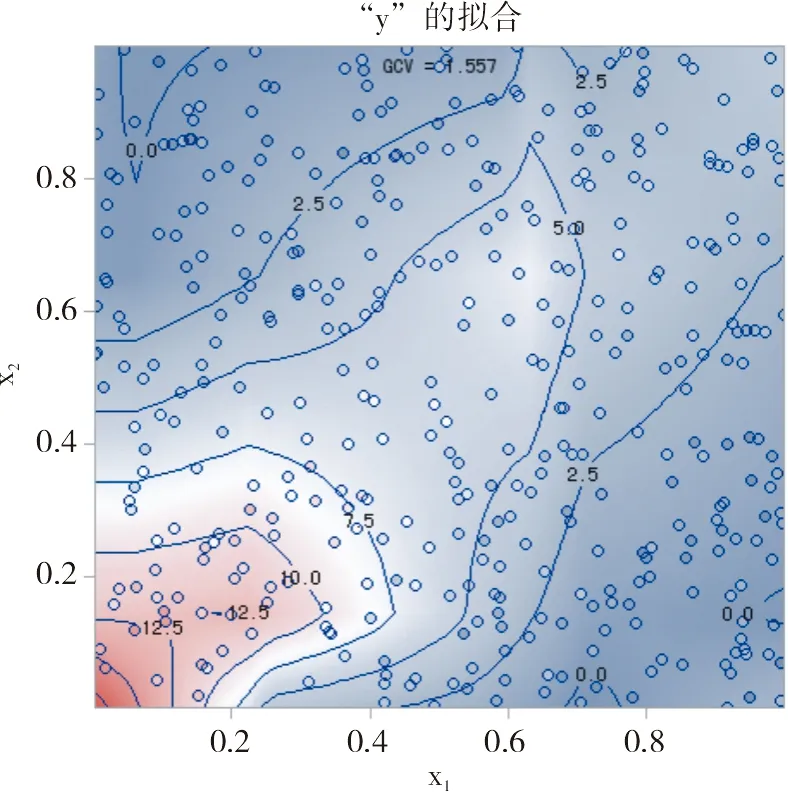
圖1 因變量y關于x1與x2的二次曲面回歸模型的等高線圖

圖1是以“等高線”形式呈現式(1)所代表的二次曲面。由于式(1)屬于三維空間里的二次曲面，無法采用二維平面圖來呈現其立體形狀。設想：采用一系列平行于二維平面的“平面”去切割三維空間里的“二次曲面”，所形成的“切口”自上而下沿垂直于縱軸y的方向投影到由(x1，x2)所形成的二維平面上，就出現了圖1中的“曲線”。每一條曲線的高度“y”是相同的，故被稱為“等高線”。等高線上標注的“數據”(例如12.5、10.0、7.5、5.0和2.5等)代表“切割平面”離“底部二維平面”的“高度”的數值。

由圖1中多條等高線的形狀可知：式(1)所代表的“二次曲面”比較復雜；若是一個“圓球”曲面模型，則其所有等高線就會形成一系列的“同心圓”。

2.2 對實例2進行適應性回歸分析

2.2.1 所需要的SAS過程步程序

在前面的SAS過程步程序的“MODEL語句”中，不寫入“ x2即可。

2.2.2 SAS輸出結果及解釋

下面僅給出最后一部分輸出結果：

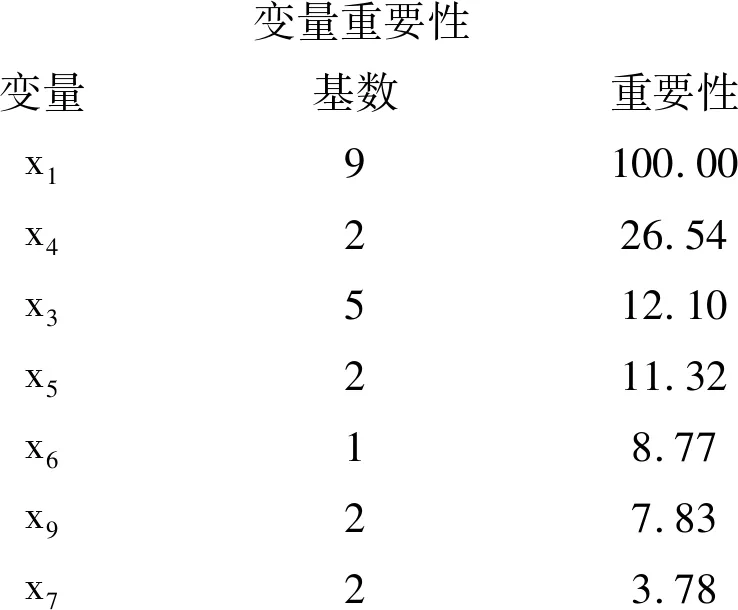
變量重要性變量基數重要性x19100.00x4226.54x3512.10x5211.32x618.77x927.83x723.78

以上結果表明：除x1真正對因變量y有影響外，還得出x4對因變量 有較大的影響；甚至還有x3和x5。而實際上，除x1之外，其他變量對因變量y沒有任何影響。

2.3 對實例3進行適應性回歸分析

2.3.1 所需要的SAS過程步程序

在前面的SAS過程步程序的“MODEL語句”中，不寫入“x1”即可。

2.3.2 SAS輸出結果及解釋

下面僅給出最后一部分輸出結果：

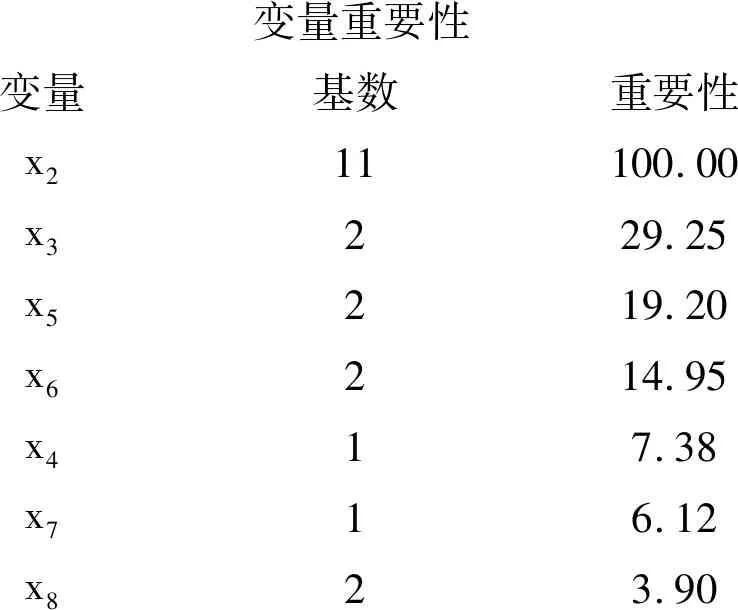
變量重要性變量基數重要性x211100.00x3229.25x5219.20x6214.95x417.38x716.12x823.90

以上結果表明：除x2真正對因變量y有影響外，還得出x3對因變量y有較大的影響；甚至還有x5和x6。而實際上，除x2之外，其他變量對因變量y沒有任何影響。

2.4 對實例4進行適應性回歸分析

2.4.1 所需要的SAS過程步程序

在前面的SAS過程步程序的“MODEL語句”中，不寫入“x1”和“x2”即可。

2.4.2 SAS輸出結果及解釋

下面僅給出最后一部分輸出結果：

變量重要性變量基數重要性x36100.00x4260.87x7242.66x8116.58

以上結果表明：在x3～x10這8個與因變量y毫無關系的變量中，得出：x3和x4對因變量y的影響很大；x7和x8對因變量y的影響也比較大。顯然，這個結果是不可信的。

3 討論與結論

3.1 討論

基于對“實例1”的分析結果來看，“ADAPTIVEREG過程”對于包含多個“噪聲變量”的數據結構具有很強的“甄別能力”，能夠“挖掘”出“隱藏”在復雜數據結構中的“真正規律”；而基于對“實例2”和“實例3”的分析結果來看，“ADAPTIVEREG過程”對于包含多個“噪聲變量”的數據結構具有較強的“甄別能力”，能夠“突顯”出“隱藏”在復雜數據結構中的“真正規律”，但也在較大程度上受到了“噪聲變量”的干擾和影響；再基于對“實例4”的分析結果來看，“ADAPTIVEREG過程”對于全部由“噪聲變量”組成的數據結構不具有“甄別能力”。

通常，真實資料的數據結構是錯綜復雜的，其是否包含有變量之間的真實數量聯系是未知的，比較可靠的做法是依據基本常識和專業知識盡可能找全找準與結果變量有聯系的“自變量”和/或“中間變量”，并適當引入由前述提及的那些變量產生的“派生變量”[3-4]。在此基礎上，盡可能使收集數據的過程受控于“標準操作規程”和“質量控制策略”[5]，確保樣本能很好地代表研究總體且具有足夠大的樣本含量。再盡可能多采用一些統計模型和技術方法去擬合數據，并基于測試數據集評估模型的擬合效果。

3.2 結論

適應性回歸樣條算法(即由“ADAPTIVEREG過程”來實現)并不是“萬能的”，它僅適合于數據結構中確實包含了“具有某種聯系的變量集合”，而并不適合于“因變量與自變量之間不存在任何數量聯系”的數據結構。