基于最優化的廣域雷場空間多節點坐標修正算法*

趙建新，張宏映，陳 兵，魏玉龍

（北方自動控制技術研究所，太原 030006）

0 引言

智能雷場是在傳統雷場基礎上的新型信息化地雷武器系統，將傳統不動雷提升為具有按照指令布局、通道自動封鎖等信息處理能力的活動雷［1］。針對室外活動節點，傳統方法采用GPS進行定位，而在野外環境下，普通GPS模塊的定位精度在10 m～15 m。在廣域雷場空間中，為實現有效區域封鎖，活動雷投放密度較高，各活動雷間距離小于3 m。基于成本和定位精度考慮，在每個活動雷中集成了UWB測距模塊，其價格較為低廉，測距精度為米級。只在部分活動雷內部集成了GPS模塊，包含了GPS模塊的活動雷稱為錨節點，其余活動雷稱為普通節點，錨節點為普通節點提供基準坐標，普通節點利用錨節點坐標通過三邊定位法完成定位。在進行活動雷布局時，根據各錨節點的GPS坐標得到的錨節點分布態勢與錨節點實際物理分布情況差距過大，導致所有活動雷間的坐標相對誤差過大，不能滿足精度要求。因此，需要對各節點坐標進行修正，較大限度降低坐標相對誤差。

1 基于最優化的廣域雷場空間多節點坐標修正方法描述

GPS的誤差包含了公共誤差、傳播延遲誤差等，其誤差具有隨機性［2］。針對廣域雷場空間中GPS坐標相對誤差較大的問題，采用了GPS與精準測距相結合的方法，利用UWB測距的高精度［3］，提高節點之間的相對坐標精度。

多節點坐標的修正過程分為4個步驟：

1）劃分區域并確定點集；

2）尋找凸多邊形；

3）頂點坐標修正；

4）其余節點坐標修正。

1.1 劃分區域并確定點集

利用錨節點的GPS坐標，對雷場區域中的各錨節點進行劃分，得到多個節點點集。該步驟實質為一個聚類過程，借鑒K-均值聚類算法并結合實際情況完成對錨節點的聚類。已知雷場區域大小，雷場區域中存在m個錨節點（其中m＞9，若m≤9，直接尋找凸多邊形），根據錨節點的GPS坐標獲得錨節點的分布情況，劃分過程如下：

1）為保證劃分的每個區域中存在6個左右的錨節點，將初始劃分區域數量設為n=m/6。

2）將雷場區域平均劃分為n個區域，得到各區域中分布的錨節點，選取與各區域錨節點平均位置距離最近的錨節點作為聚類中心；若該區域中無錨節點，則將該區域歸入鄰近區域；最終得到n個聚類中心。

3）利用GPS坐標計算各錨節點到各聚類中心的距離，若某個錨節點距離第i個聚類中心更近，則將其歸入i中心的點集中；若存在聚類中心的點集為空，則淘汰該聚類中心，將其作為錨節點參與劃分；最終得到n個點集。

4）分別計算各點集中的平均位置，選取與平均位置距離最近的點作為新的聚類中心。

5）遞歸執行步驟3）～步驟4），直到聚類中心不再變化；各聚類中心的點集即為得到的點集。

雷場示意圖及聚類過程如圖1所示，雷場中存在22個錨節點，將雷場分為4個區域；得到4個初始聚類中心，圖1中的星形即為各聚類中心；執行步驟3），淘汰聚類中心4，區域4并入區域3；執行算法，最終得到的聚類結果如圖1所示，得到3個點集。

圖1 雷場示意圖及聚類過程

1.2 尋找凸多邊形

分別在每個點集中遞歸尋找m個錨節點（其中m≥3），各錨節點可以組成一個凸多邊形。

以點集M中最靠近中心位置的點作為原點O，建立高斯坐標系，將剩余點分配到各象限中，將集合中M的點按照與原點的距離遠近重新排序。

推理得到，已知凸多邊形N，其邊數為n，判斷某一點B能否與其組成凸n+1邊形的條件為：

1）B點不在多邊形N內；

2）多邊形各相鄰邊反向延伸得到n個區域，B點不在這些區域內。

以四邊形為例，如圖2所示，若點B不在四邊形 N 內，且不在區域 P1、P2、P3、P4內，則 B 可與四邊形N組成凸五邊形。

圖2 四邊形與點B組成凸五邊形條件示意圖

采用直接法尋找凸多邊形，如圖3所示，步驟如下：

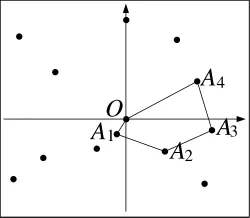
圖3 直接法尋找凸多邊形

1）以原點O為圓心，將集合M中與原點距離小于0.2 m的節點剔除，遍歷尋找M中與原點距離最近的點A1。

2）在集合M中尋找點A2，使得A2與A1、O點可以組成三角形。

3）遍歷尋找A3點，A3可與找到的點組成凸多邊形，過程中對不滿足條件的點進行剔除。

4）遞歸執行步驟3），直至完成遍歷。

1.3 頂點坐標修正

得到凸多邊形后，利用節點坐標修正模型對各頂點進行修正，得到修正坐標。

1.4 其余節點坐標修正

分別利用各點集中的凸多邊形頂點坐標，通過三邊定位方法計算各點集中其余錨節點坐標，再利用測距結合三邊定位方法得到各普通節點坐標。

2 節點坐標修正模型

從某一點集中獲取凸多邊形后，利用UWB測距值結合GPS坐標對頂點坐標進行修正。

2.1 模型建立

假設獲取的凸多邊形為M，其邊數為k，已知M中k個頂點的GPS坐標，利用GPS坐標可以確定M的形狀和位置；利用UWB測距可以得到各頂點間兩兩距離。通過三角形穩定性原理，在得到了多邊形M的所有邊和對角線的精準長度后，可以確定一個新的多邊形N。由于UWB的精度遠高于GPS，故多邊形N的形狀比M更符合各頂點的實際分布形狀。當多邊形邊數為6時的M和N的示意圖，如圖4所示。

圖4 六邊形示意圖

已知多邊形M中各頂點坐標，得到M的中心O，將多邊形N的中心與O重合，M不動，以O為圓心旋轉多邊形N，當N的各頂點距離與M的各頂點的距離和最小時，多邊形N的各頂點坐標即為修正后的坐標。當多邊形邊數為6時的修正示意圖如圖5所示，圖中要求（AA1+BB1+CC1+DD1+EE1+FF1）最小。

算法轉化為最優化問題［4］，假設多邊形邊數為k，則 k 邊形 M 中各頂點的坐標為（α1，β1），…，（αk，βk），k 邊形 N 中各頂點的坐標為（x1，y1），…，（xk，yk），約束條件如下：

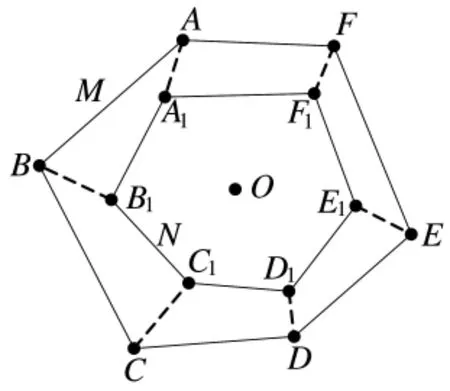
圖5 修正示意圖

1）k邊形N和k邊形M的中心O重合；

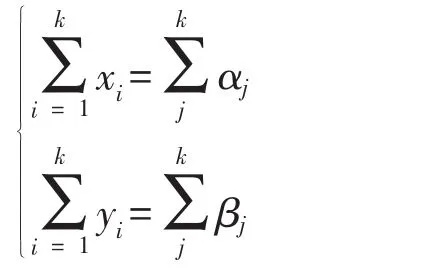
2）k邊形N各邊距離和對角線距離dij（其中i≠j）已知；

求k邊形N各頂點與k邊形M各頂點距離和最小，得到目標函數如下：

最優化問題通常采用拉格朗日乘子法將帶約束條件的最優化問題轉化為解方程組問題，當方程組維度超過8時，求得最優解的方法較為復雜且費時［5］，模型通過對多邊形進行順時針旋轉，將多維問題優化為一維問題。

2.2 模型優化

以k邊形M的中心O為原點建立高斯坐標系，k邊形N的中心與O重合，已知M中頂點坐標分別為（α1，β1），…，（αk，βk），N 中各邊長度和各對角線長度dij（其中i＝1，…k；j=1，…k；i≠j），推導得出原點O與某一頂點長度為：

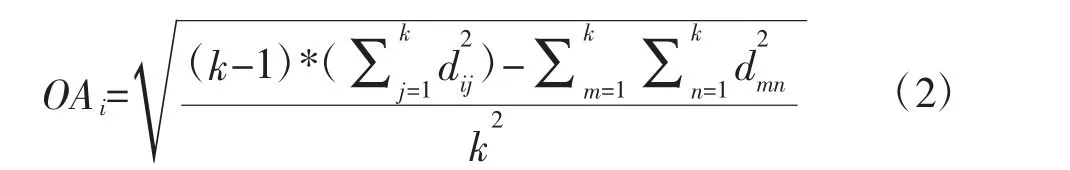
其中，j≠i，m≠n≠i。

以五邊形為例，O與A1之間的距離為：

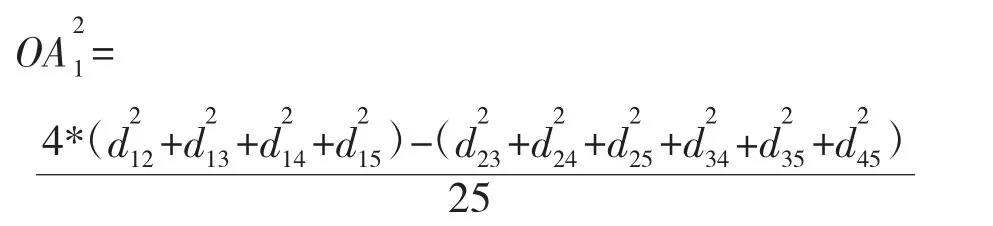
將N中的頂點A1的橫坐標設為X1，通過式（2）得到，結合X1得到A1的縱坐標Y1，進而得到k邊形N中其余各頂點的初始坐標。

以O為圓心，k邊形N以順時針進行旋轉，旋轉角度為θ，旋轉過程中k邊形N各頂點坐標為：

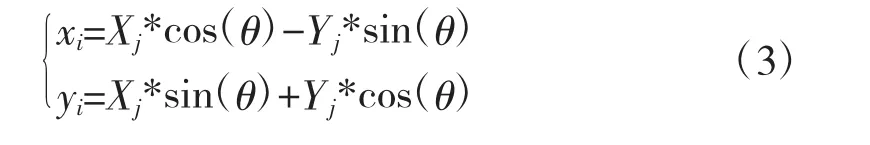
其中，i=1，…k；Xj≠Yj為各項點初始坐標。

旋轉模型示意圖如圖6所示。

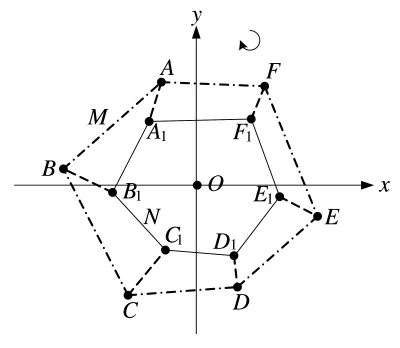
圖6 旋轉模型示意圖

通過旋轉使得N的各頂點距離與M的各頂點的距離和最小，結合式（3）得到目標函數為：

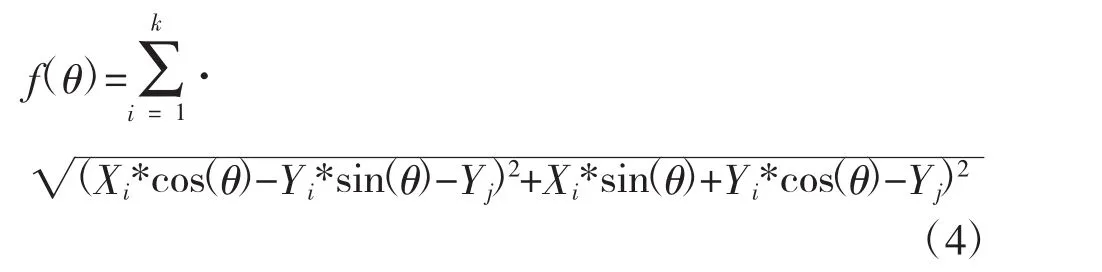
其中，Xj，Yj為各項點初始坐標。

模型最終轉化為求單變量θ使f（θ）值最小的問題，通過極值法得到θ值后，將θ帶入式（3）中，得到各頂點的修正坐標。

3 算法實驗測試

實驗選擇90*90 m的區域作為雷場區域，選取總共40顆活動雷，其中錨節點15個，其余為普通節點，各活動雷在雷場區域隨機分布，節點實際分布示意圖如圖7所示。其中，用圓圈表示的節點為錨節點，雪花表示的節點為普通節點。

圖7 節點分布圖

對區域所有節點執行修正算法，將雷場區域劃分為圖8中虛線分割的3個區域，每個區域中的節點組成一個點集，各點集中分別尋找出六邊形、四邊形和三角形。

分別對3個多邊形執行坐標修正，以六邊形為例，各頂點的修正結果如圖7所示。圖中短劃線組成的六邊形的6個頂點為錨節點實際分布位置，點虛線組成的六邊形的6個頂點為錨節點利用GPS得到的坐標分布位置，實線組成的六邊形的6個頂點為經過校準后的坐標分布位置。

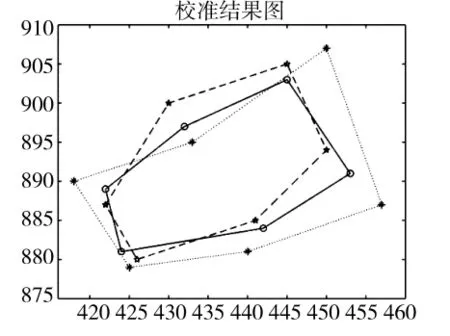
圖8 校準結果

最終修正過后的所有節點態勢分布圖與實際分布圖對比，如圖9所示。

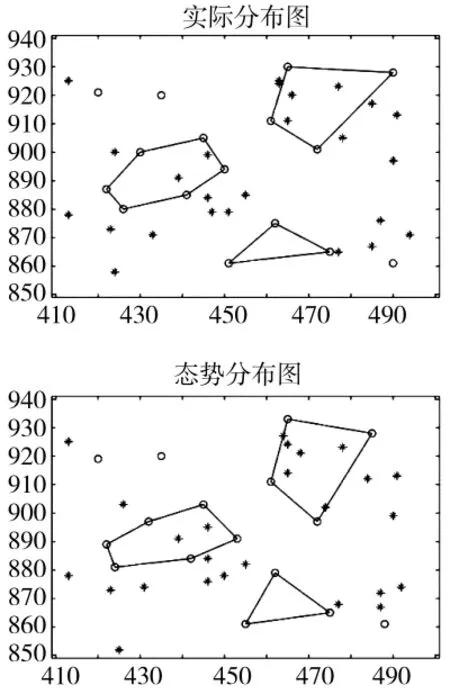
圖9 修正后的態勢分布與實際分布對比

4 結論

從實驗結果來看，利用GPS得到的坐標與錨節點實際分布存在較大偏差，通過節點修正模型以提高錨節點坐標與實際分布的一致性，降低各節點之間坐標的相對誤差。在實際應用中，算法還有很多地方需要改善，如穩定性方面需要進一步提高。