基于Cholesky分解的自適應抗干擾算法

齊志強

（中國空空導彈研究院，河南 洛陽 471009）

0 引言

衛星導航定位系統目前已廣泛應用于精確制導武器系統和其他需要導航定位的平臺上，如飛機、船舶、車輛等。衛星導航定位系統采用擴頻技術，到達地面的信號強度比白噪聲低20 dB左右，工作頻率固定，很容易遭到敵方的壓制干擾而導致無法正常工作［1］，因此，抗干擾能力成了制約衛星導航定位系統應用的瓶頸［2］。為了滿足在復雜電磁環境下的應用需求，軍用衛星導航定位產品多采用陣列處理天線來提高抗干擾能力［3］。

目前采用陣列信號處理來進行衛星定位系統的抗干擾處理算法主要有兩大類:一類是閉環算法，另一類是開環算法。常用的閉環算法以LMS算法為典型代表，該算法實現簡單，計算量小，因而成為美軍早期采用的主要的抗干擾算法。但該算法的收斂速度與其輸出協方差矩陣的特征值分布相關，其收斂速度隨著干擾信號強度和干擾信號的類型變化而變化，當特征值散布較大時，收斂速度慢［4］，特別是在動態載體上難以收斂到最優值。開環算法的收斂速度快，被認為是實現自適應抗干擾處理的最優算法［5］，已成為國內外研究的熱點方向。開環算法主要有多級維納濾波MSNWF（Multistage Nested Wiener Filter）和 SMI（Sample Matrix Inversion）算法［6-7］，MSNWF算法雖然具有良好的降秩性能，但降秩處理會影響陣列自由度，使干擾抑制性能下降［8］，而且MSNWF算法包含前向迭代和后向迭代，當振元數目過多時，計算量迅速增加，難以滿足實時性的要求［9］。傳統的SMI算法需要進行矩陣求逆運算，硬件系統復雜［10］，實現困難［11］，為解決此問題，通常用矩陣分解的方式來實現。本文主要闡述基于Cholesky分解的自適應抗干擾算法應用研究。

1 自適應抗干擾算法

衛星導航定位系統由于接收到的信號比較弱，湮沒在白噪聲中，而干擾信號比較強，常用的抗干擾算法主要有自適應調零和自適應波束形成技術，自適應波束形成技術被認為是干擾抑制最有效的工具之一［12］。文獻［12］推導的自適應波束形成算法最終需要求得的權值表達式為:

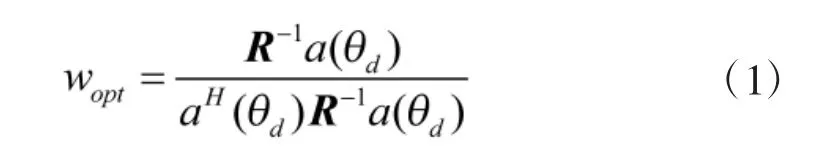
式（1）中，a（θd）為陣列在 θd方向的陣列響應，R 為輸入信號的協方差矩陣，a（θd）和 R 的求解在文獻［12］中已有詳細的推導，這里不再重復。從式（1）中易見，權值求解的關鍵在于求得協方差矩陣R的逆矩陣。

2 矩陣求逆的方法

自適應抗干擾算法的主要運算，最終歸結為對輸入信號的協方差矩陣求逆問題。矩陣求逆的方法較多，而矩陣求逆方法的選擇不僅關系硬件資源的占用量，還關系著權值的更新速度。因此，對于硬件平臺來說，由于硬件資源有限，需要找到一種既耗費資源少，又可以快速完成矩陣求逆的方法。

矩陣求逆最基本的方法是Gauss消元法，但該方法計算步驟繁多，運算量大，不適合硬件實現。硬件實現時通常采用矩陣分解的方法，將矩陣轉換為特殊矩陣，從而簡化運算。矩陣分解常用的方法有LU 分解［13］，QR 分解，Cholesky分解等方法，LU 分解結果不唯一；QR分解需要將矩陣分解為一個正交矩陣和一個上三角矩陣，并且需要求平方和開根號，步驟繁多，利用硬件實現比較困難［14］；Cholesky分解需要用到開方和除法，不太適合FPGA實現，但近年來隨著FPGA的規模越來越大，用FPGA來完成Cholesky變換，資源問題已不再成為問題的瓶頸［15-16］，因此，本文擬采用Cholesky分解來實現權值求解。

3 Cholesky分解求權值方法

R是秩為n的赫米特矩陣，利用Cholesky分解可求得下三角矩陣G，使R=GGH。

矩陣R可以寫作如下形式:

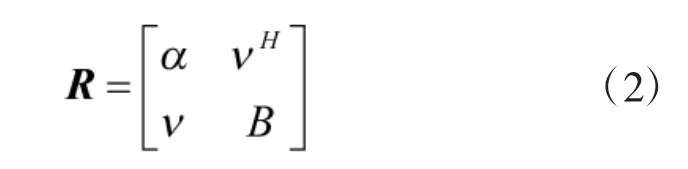
則存在下三角矩陣:

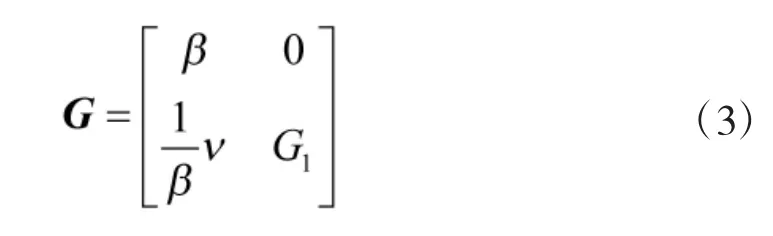
由式（3）可知，要得到矩陣G，需要分3步走:

第3步:求解矩陣G1。令，則有，G1為下三角矩陣，顯然，矩陣G1的求解過程和矩陣G的求解過程相同，先算出矩陣R1，然后采用相同的方法即可逐步求出矩陣G1中的全部元素。

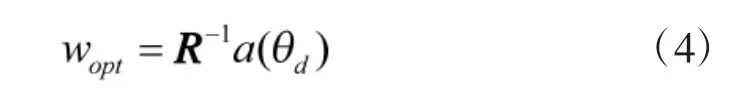
將式（4）兩邊同乘以 R，并將R=GGH帶入，可得:

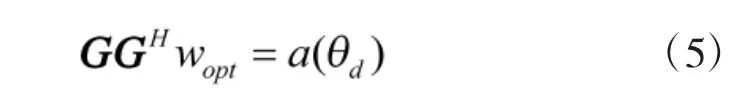
式（5）中 a（θd）為 n×1 的列向量，G 為 n×n 的下三角矩陣，令，則T為n×1的列向量，式（5）可以寫為:

式（6）可以用Gauss消元法求得T，以n=4為例，式（6）可以寫為:

由式（7）可求得 T，

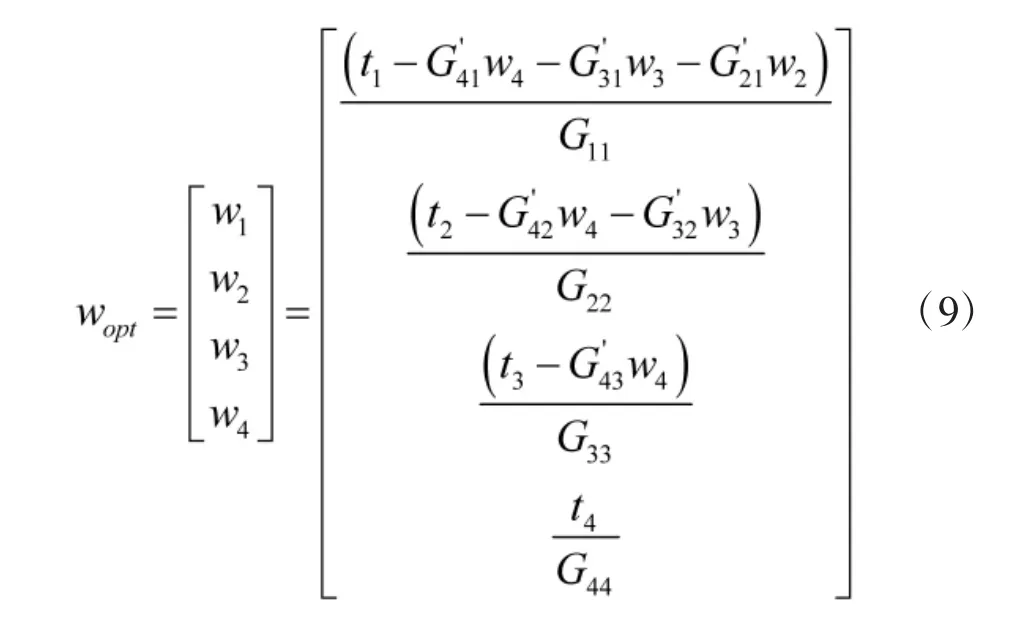
4 FPGA實現

用FPGA實現Cholesky分解求權值，需要3個功能模塊，如圖1所示:

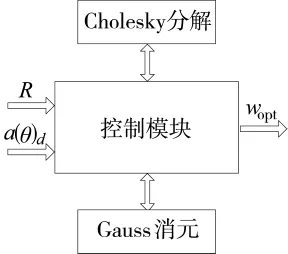
圖1 Cholesky分解求權值模塊結構圖

控制模塊負責協方差矩陣R和導向矢量a（θd）的調取，協調Cholesky分解模塊和Gauss消元模塊的數據進出及時序控制，并將最終求得的權值輸出。

Cholesky分解模塊完成對協方差矩陣R的分解，求出下三角矩陣G。由上面的介紹可知，Cholesky分解由3個計算單元組成:第1個計算單元進行開方運算，求出矩陣G的第1個元素，；第 2個計算單元求出矩陣G的第1列其他元素，；第3個計算單元更新下三角矩陣中的其他元素，即求出。由于下三角矩陣G1為n-1維矩陣，因此，上述3個計算單元可在控制模塊作用下重復利用，最終完成下三角矩陣G的求解。

Gauss消元模塊只需要一個計算模塊即可完成兩次Gauss消元的全部運算，以4振元為例，只需完成計算模塊，當計算t1時，控制模塊將a1賦給a4，將G11賦給G44，其他元素賦0即可，在控制模塊作用下，依次算出 t1，t2，…，t4。

上述計算過程多是順序執行，需要幾百個時鐘周期才可以完成一次權值更新，但協方差矩陣也是需要多個時鐘周期的樣本數據才可求得［12］，即使1 000個時鐘周期更新一次權值，以系統時鐘62 MHz為例，更新周期也只有16 μs，足以滿足高動態條件下的權值更新要求。

表1列出了幾種常用自適應抗干擾算法的比較情況，其中M代表陣列的維數，D表示MSNWF降秩后的維數。

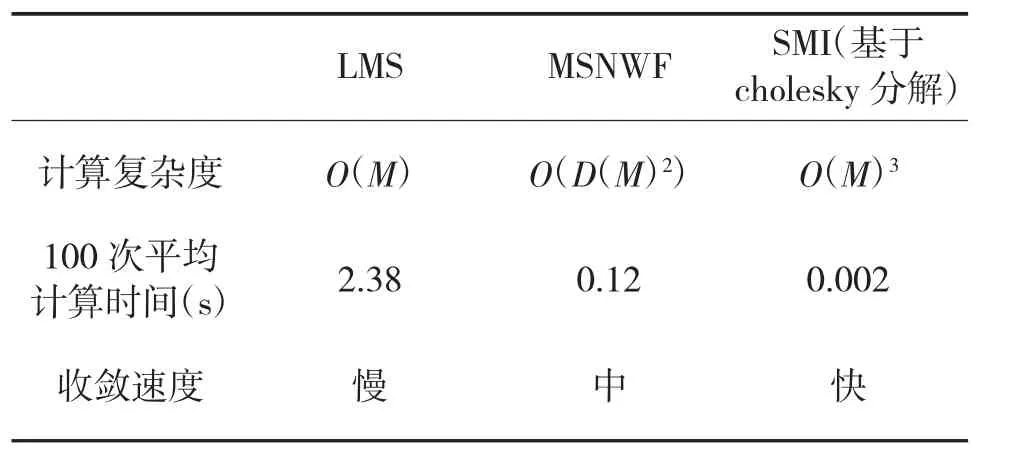
表1 幾種常用自適應抗干擾算法的比較

從表1可以看出，SMI算法性能最優，但計算復雜度也最高，因為該算法需要開方和除法運算，這也是很多人望而卻步的原因。本文所述方法由于可以實現資源復用，僅需要1個開方模塊和1個除法模塊，乘法器也可以復用，cholesky分解所需乘法器數量僅和LMS算法相當，因此，該算法對資源的需求并不是特別大，完全可以用FPGA來實現。

5 結論

本文所述的基于Cholesky分解的自適應抗干擾算法巧妙地回避了矩陣求逆運算，大幅度降低了運算復雜度，掃除了利用FPGA實現的障礙。按照文獻［12］所述方法，已在工程上實現，其抗干擾效果可達80 dB以上，特別是在高動態載體上，依然可以獲得優異的抗干擾性能。該方法不但可以應用于空域抗干擾技術，也適用于空時抗干擾算法，應用前景廣泛。當載體姿態不易獲知時，可以將導向矢量a（θd）設為固定值，以4振元為例，當時為常用的功率倒置算法［17］，時則為Capon空域自適應抗干擾方法，當時為空時聯合抗干擾方法［18］。