推力對艦載導彈出筒姿態的影響研究*

李顯龍，瞿 軍

（1.解放軍91206部隊，山東 青島 266108；2.海軍航空大學岸防兵學院，山東 煙臺 264001）

0 引言

艦艇作為海上發射平臺是受到海洋環境影響的，而且運動狀況無法被準確預測，然而導彈從剛出筒到進入起控點的這段飛行是無控狀態的，一旦導彈出筒姿態發生較大偏差，可能無法對其進行糾正，最終會導致發射失敗［1］。一般而言艦載導彈出筒姿態的偏差主要是由艦艇在海面上的運動造成的，因此，如何有效減小這種影響是目前國內外研究的重點之一。目前解決該問題的方式主要為在艦艇端進行消揺，從而達到滿足發射條件的目的，因此，本文針對導彈出筒姿態的優化問題進行研究。

目前，針對高海情條件對導彈發射擾動問題，國內的研究主要聚焦于艦艇運動帶來的最大可能擾動，一般將最大過載時刻視為最大擾動時刻，并且將最大過載分為XYZ 3個方向分別進行討論，例如文獻［2-5］。這種研究方法可以有效簡化計算量，但也存在不足，由于最大過載矢量和的模可能大于3個分量值，因此，得到的結果也就不夠準確。

本文針對艦艇的運動特點進行了研究，建立了艦艇運動的數學模型。分析了艦艇運動時可能對導彈出筒影響的過載，并且用MATLAB軟件進行了仿真計算，求得了過載的矢量之和。用計算機建立導彈發射多剛體模型，通過在這些時刻進行發射仿真研究，并改變推力的大小，找出推力和導彈出筒的姿態角定量關系。為高海情條件下艦載導彈的發射安全性提供參考依據。

1 艦艇的搖擺運動

1.1 運動形式

對于艦艇運動的研究，工程上一般將其近似視為簡諧運動進行研究。艦艇在海面上的運動如空間中自由運動的物體有6個自由度，對應的6種運動稱為:橫搖、縱搖、艏搖、橫蕩、縱蕩以及垂蕩。這6種運動當中，橫搖、縱搖、垂蕩由于受到恢復力和恢復力矩的作用，可以恢復到初始位置［6］，因此，可視為簡諧運動，且對導彈發射的初始姿態的影響相對其他3種大得多，因此，本文主要考慮橫搖、縱搖、垂蕩對垂直發射的影響［5］。以艦艇的質心為坐標原點，建立三維笛卡爾地面坐標系OXYZ，艦艇坐標系OXVYVZV，艦艏朝向X軸的正方向，豎直向上為Y軸正方向。用正弦函數描述這3種運動的運動方程可表示為:

式中，γ、θ分別為橫搖和縱搖運動的角度量，γm、θm為縱搖和橫搖角度的幅值；而η為艦艇質心垂蕩運動的位移量，ηm為垂蕩運動的幅值。

將導彈質心在艦艇坐標系OXVYVZV中的坐標設為:

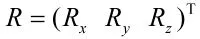
由式（1）可以得到艦艇橫搖、縱搖運動同時出現時的角速度:

寫成向量的形式為:

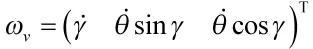
由此可求得艦艇搖擺運動的線速度:

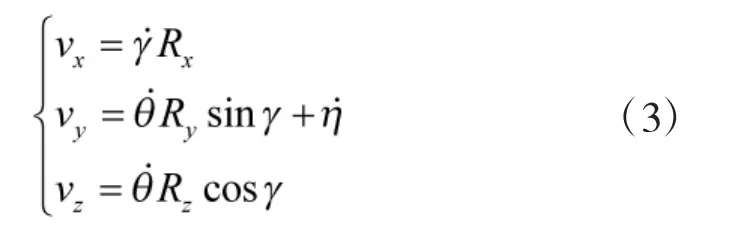
式中，R為在艦艇坐標系中導彈質心的坐標。

1.2 運動過載

艦艇運動引起的導彈在發射時的總過載包括搖擺運動及垂蕩運動所帶來的過載系數矢量之和［4-5］:

式中，n為導彈在發射過程中由于艦艇的運動受到的過載總和。為搖擺運動過載，為升沉運動過載。而艦艇搖擺運動（橫搖、縱搖）過載用表示:

其中，ne和nk分別為導彈質心繞艦船搖擺運動軸而運動時產生的牽連過載系數和科氏過載系數。其中牽連過載系數為:

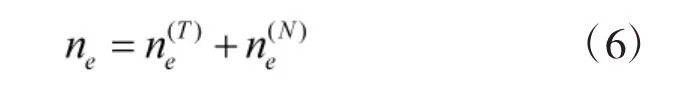
1.2.1 升沉過載

導彈的升沉運動與艦艇的升沉運動相一致，同為Y軸方向的簡諧運動，因此，有:

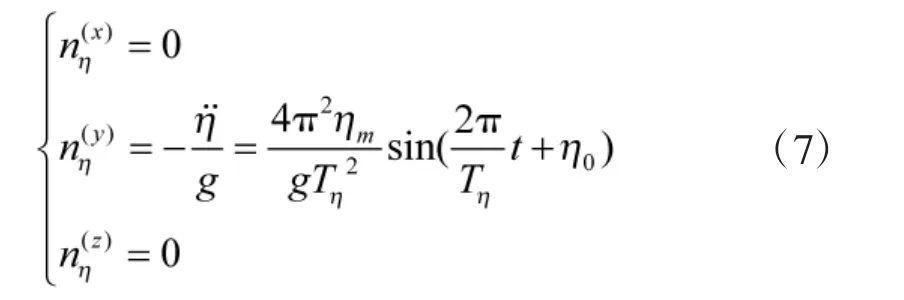
1.2.2 牽連過載

所謂牽連過載，即導彈質心圍繞艦艇質心運動而產生的過載。而牽連過載又分為法向和切向［8］。其中切向過載系數為:

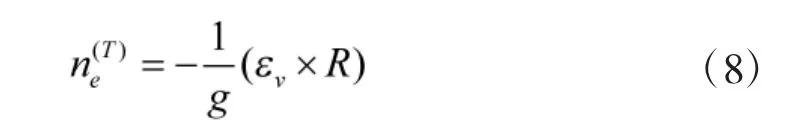
εv為艦艇搖擺運動的角加速度，R為在艦艇坐標系中導彈質心的坐標。

對角速度ωv求導得:

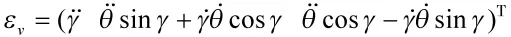
將其代入式（1）中從而得到:

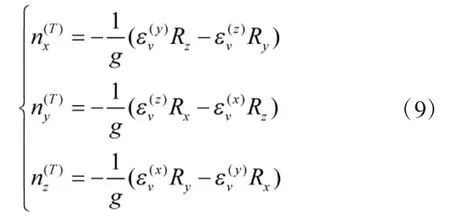
式中，Rx、Ry、Rz分別為導彈質心在 X、Y、Z 3 個坐標軸上的坐標，分別為X、Y、Z 3個方向的切向牽連過載系數。

除切向過載外，搖擺運動還會帶來垂直于瞬時運動方向的法向過載，與切向過載同屬于牽連過載范疇:

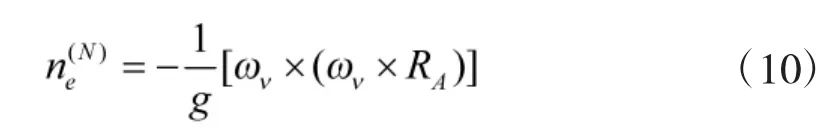
1.2.3 科氏過載

科氏力產生于慣性坐標系內物體在動系中有相對運動速度，即艦艇搖擺運動時導彈在發射筒內相對于發射筒運動。

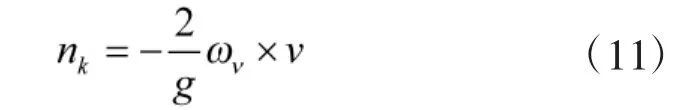
其中，ωv為艦艇搖擺運動的角速度向量，v為導彈相對發射筒的相對速度，從而得到:

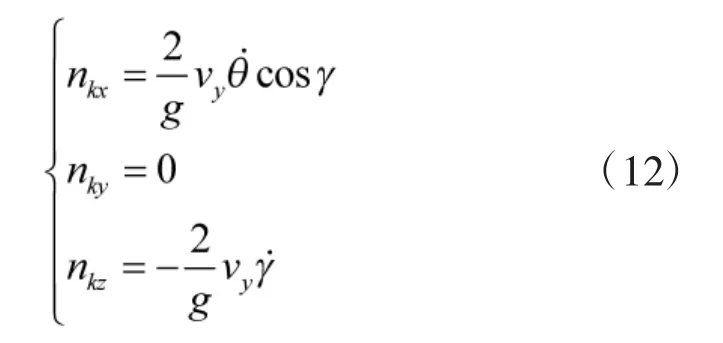
所得科氏過載無方向分量。

1.2.4 總過載

將式（7）、式（8）、式（10）、式（12）相加得到的總過載為:

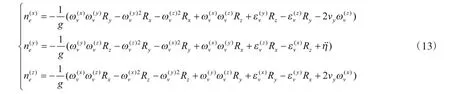
2 導彈彈射原理

2.1 物理模型

艦載導彈垂直冷發射裝置安裝于艦艇的甲板之下，彈射裝置集成于發射筒當中。為方便對其建模仿真，對其結構進行簡化處理。

該發射系統由發射筒、發射筒蓋、導彈、前后兩組滑塊以及托架組成［9-10］。采用垂直冷發射的方式發射導彈，導彈置于發射筒底部的托架之上，發射時高壓的燃氣蒸汽迅速推動氣缸帶動托架將導彈向上推出，托架運動到筒口位置時碰到緩沖器停止運動與導彈分離［10］。

導彈與發射筒之間通過滑塊與導軌的接觸約束相連接，滑塊與導彈彈體視為一體，導軌位于發射筒內壁。為防止導彈在發射筒當中運動不暢，采用間隙配合的方式［11］，保證滑塊與導軌之間存在一定的距離。

導彈長細比相對合適，將其視為剛體，不會因彈射產生形變。忽略導彈質量偏心和折疊彈翼展開等無關因素對該問題的影響。

2.2 約束添加

2.2.1 碰撞力

導彈的運動由托架帶動，滑塊與導軌之間也存在間隙，故相互之間會產生碰撞，對于碰撞問題本文采用Contact接觸碰撞模型。碰撞函數使用Impact，該函數用于抗壓縮的非線性的彈簧阻尼方法近似計算單邊碰撞力。

圖1 簡化結構

式中，q0為兩物體恰好沒發生接觸關系的距離；q為物體之間的實際距離，q0-q為接觸點的切入深度（Penetration Depth）；e為作用力指數（Force Exponent），一般取值大于 1，橡膠材料取 2～3，金屬材料一般為1.3～1.5之間；c為阻尼系數，使用step函數對其進行修正。2.2.2 彈射曲線

彈射力是由燃氣發生器產生的高壓燃氣迅速進入到氣缸中并帶動托架向上運動產生［14］，本文針對彈射曲線進行了等效和簡化。作用點為托架質心位置，采用 step（x，x0，h0，x1，h1）函數設置彈射力曲線。由于閉鎖力的存在，假設該力從0時刻開始即為額定值，托架到達預定位置后迅速停止，即x1與x0之間間隔很短。

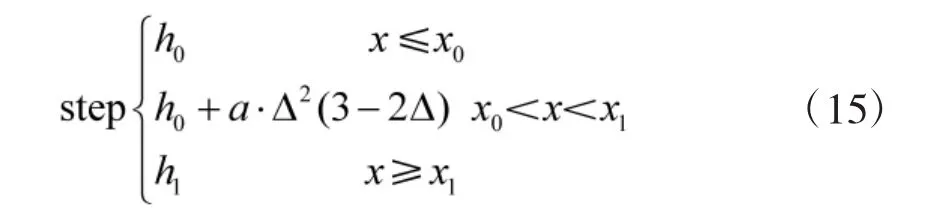
3 仿真計算與結果分析

在MATLAB軟件中設置仿真步長0.01 s，仿真時長50 s，代入發射裝置在艦艇上的位置坐標，分別針對4級～6級海情下的艦艇運動過載系數進行仿真計算。艦艇的運動參數如表1所示［12-14］。

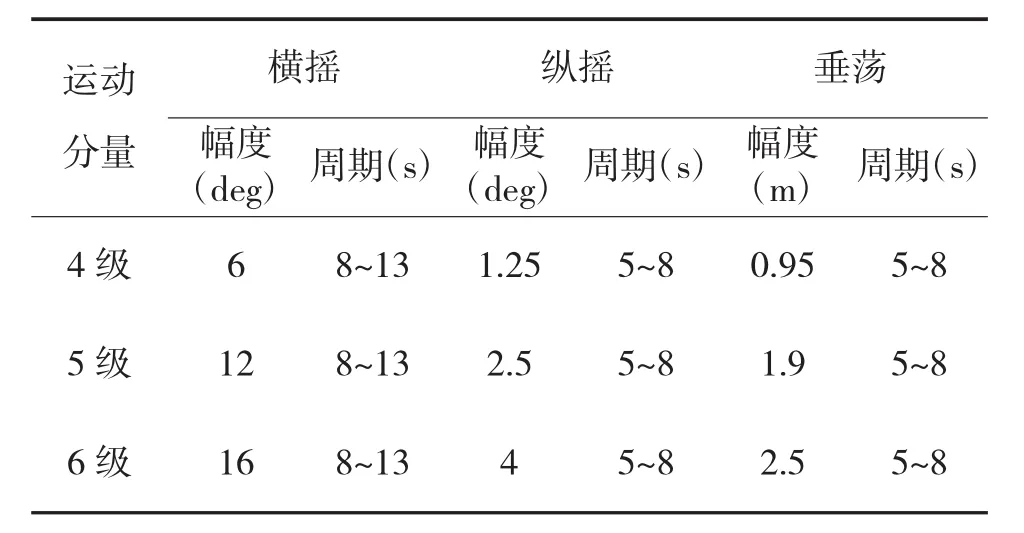
表1 大型船舶不同海況下的運動幅值及周期

所得XYZ 3個方向的過載大小如圖2～圖4所示:

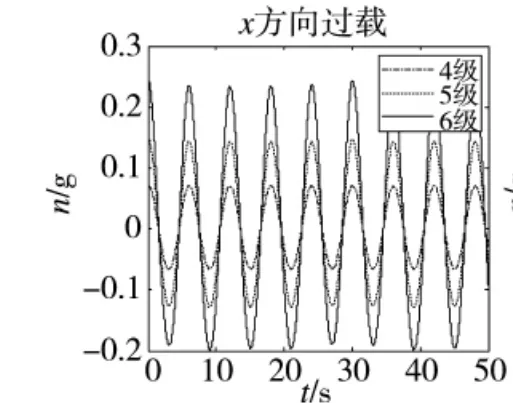
圖2 x方向過載

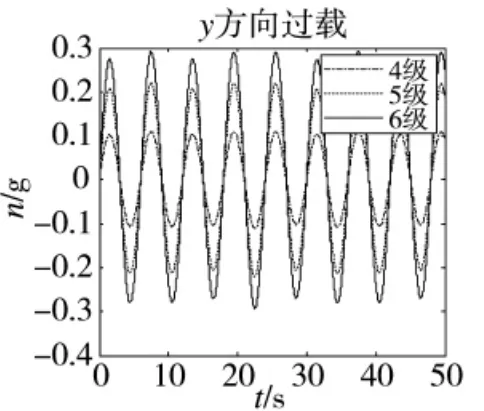
圖3 y方向過載

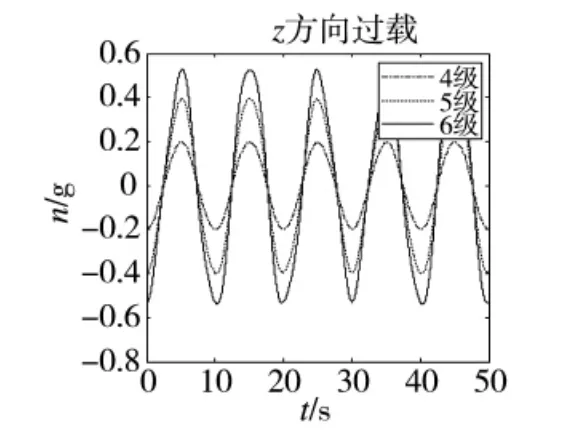
圖4 z方向過載

圖2～圖4分別為X、Y、Z 3個方向的過載分量，而大多數關于艦艇搖擺過載對發射影響的研究針對過載分量，但在實際情況中，分過載的矢量和往往大于3個方向的過載分量，為得到總過載的最大值，采用對矢量求和的方法:

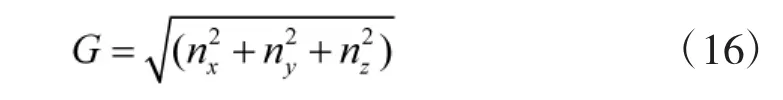
式中，nx、ny、nz為 X、Y、Z 方向的總過載；G 為總過載。

所得過載之和如圖5所示。

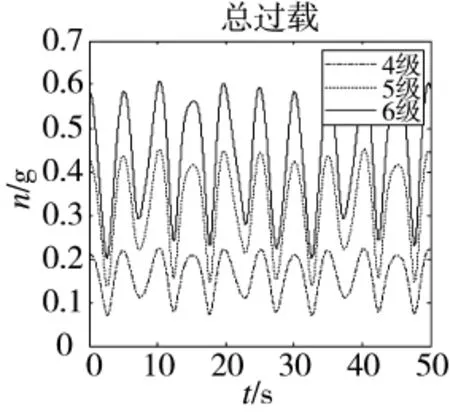
圖5 總過載

將MATLAB仿真數據代入ADAMS軟件中進行仿真模擬，模型參數設定完畢后，輸入仿真時間和步長開始仿真。開始時由于托架對導彈的沖擊，導致加速度大小出現較大波動，約0.05 s后穩定在170.7 m/s2，導彈速度在0.15 s達到最大值24.8 m/s，之后以重力加速度做勻減速運動。將仿真時間延長至3.5 s，導彈于0.37 s時刻離筒，2.30 s時達到最大高度23.2 m，之后高度開始下降。

假設導彈彈射高度≥20m時才能點火，在220KN推力作用下需要約2.2 s，因此，將2.2 s時刻導彈的姿態角為評價標準，并且將4級海情下導彈的總偏角作為100%，仿真圖像如圖6所示。

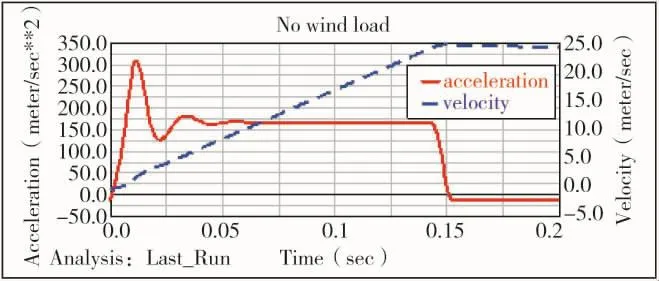
圖6 彈射加速度和高度

艦艇的運動和導彈的彈射均從0.3 s開始，將仿真時間設定為2.5 s，該時刻對應的角度即為所求。定義俯仰角和偏航角分別為導彈繞z軸的轉角和繞x軸的轉角；偏角為導彈軸線與鉛垂線的夾角，將所得數據經整理后見下頁表2。

在軟件中將導彈出筒時的彈射推力增大后得到的偏角（在過載的矢量和最大時發射得到）有明顯變小趨勢。為得到推力增大后與偏角之間的定量關系，假設某艦艇在4級海況下可以保證導彈正常發射，超出該海況條件可能發生危險，故改變導彈出筒時的彈射推力，將5級和6級海情下導彈出筒的總偏角達到4級海況時的水平（誤差控制在1%以內），得到的推力大小如表3所示。

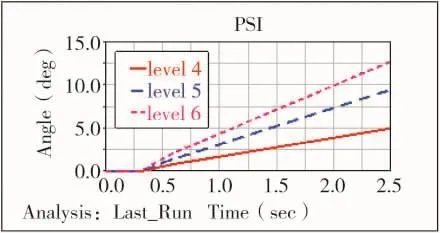
圖7 導彈俯仰角

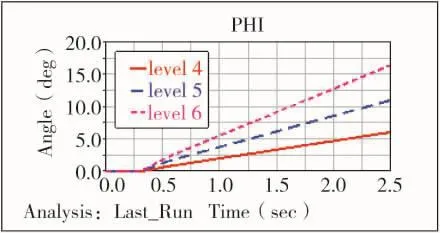
圖8 導彈偏航角

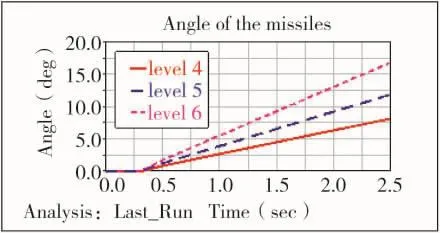
圖9 導彈偏角

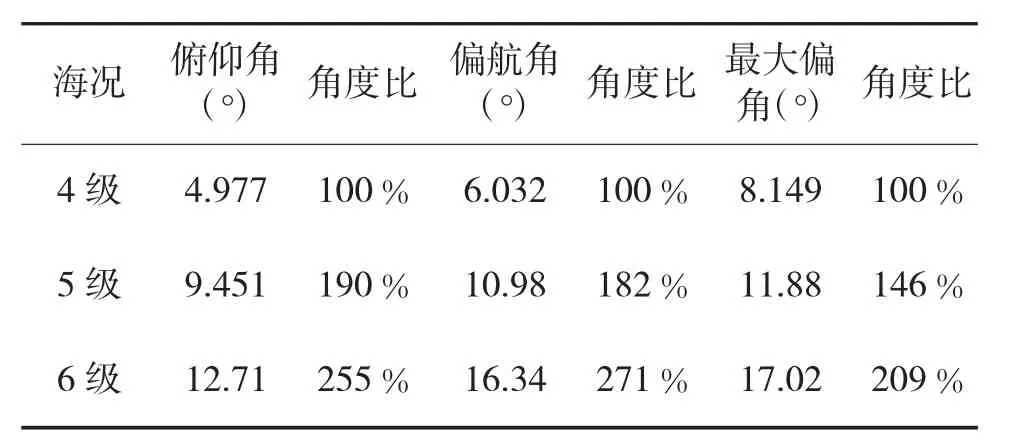
表2 推力220 KN情況

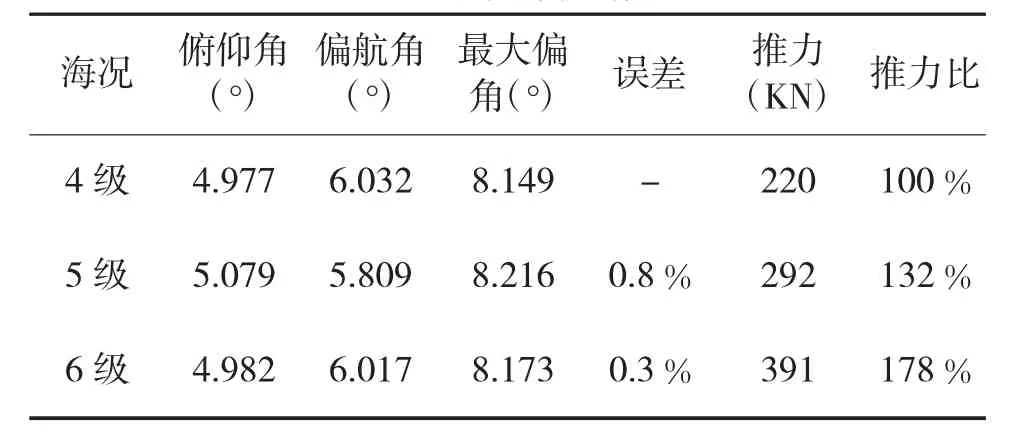
表3 改變推力情況

由表2和表3對比可以看出，4級～6級海況下，其偏航角和俯仰角的差別相對較大，若將4級海情時的姿態角作為標準100%時，5級海況下的俯仰角和偏航角分別比4級時高出90%和82%，而6級時更是高出4級的155%和171%。調整彈射推力大小使得偏角達到4級海情時的水平，5級海情時推力提高32%，對應偏角幅度下降46%，6級海情下推力需提高78%，對應偏角降低了109%。根據仿真結果提高推力對減小艦載導彈發射的初始姿態角起到了一定的作用。

4 結論

本文針對艦艇運動對導彈冷發射的軌跡和姿態造成的偏差進行仿真分析，基于海情等級確定了推力和姿態角的簡單定量關系，并嘗試通過改變推力的方式使姿態角減小到允許狀態。仿真結果顯示:增大推力可以達到優化艦載導彈出筒姿態角的效果。若某艦艇的導彈武器系統允許發射最高海情為4級，那么當海情達到5級甚至6級時，需要將彈射推力分別提高32%和78%，同樣可以滿足發射條件。在理論上為導彈出筒姿態的優化提供了方法，在實際情況下導彈的彈射推力可通過改變閉鎖力進行小幅改變，若海情超出允許值較大時，工程上實現的難度較大。