《和的奇偶性》教學設計

衡雷

教學內容： 蘇教版《數學》五年級（下冊）第50-51頁。

教學目標：

1.使學生通過自主探究與合作交流，了解兩個或幾個數的和的奇偶性，初步發現其中所蘊含的數學規律。

2.使學生經歷舉例、觀察、猜想、驗證、歸納、總結等數學活動過程，感受由具體到抽象、由特殊到一般的探索發現方法，進一步發展數學思維。

3.使學生進一步積累數學活動經驗，增強與他人合作交流的意識，增進對數學學習的積極情感。

教學難點：探索、發現和的奇偶性規律。

教學重點：能判斷兩個數或幾個數和的奇偶性。

教學過程：

一、課前復習：溫故知新

提問：誰來說說什么數是偶數？什么數是奇數？

生1：能被2整除的數;是2的倍數的數叫做偶數;個位是0、2、4、6、8這樣的數。

生2：不能被2整除的數;不是2的倍數的數叫做奇數;個位是1、3、5、7、9這樣的數。

提問：不去數，你能一下子就看出它們的個數是奇數個還是偶數個？

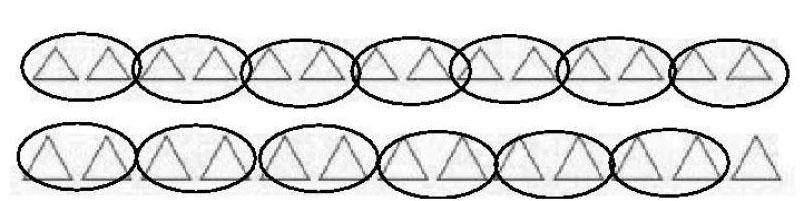
生：兩個兩個一圈，看最后是一個還是兩個三角形，如果最后是兩個，說明是偶數個;如果最后是一個，說明是奇數個。

提問：能聽明白嗎？誰來解釋一下？為什么要兩個兩個一畫（一圈）？

生：最后還剩1個三角形，說明總數是奇數個三角形。兩個一圈就相當于除以2。

【設計意圖】新課伊始，教師通過復習回顧，了解學生對奇數和偶數特征的掌握情況，對學情做到心中有數，為后續課堂教學提供一份基本的數據，使課堂教學更具有針對性。讓學生通過簡單的復習，用圖文并用的方式喚起學生已有的認知，用數形結合的形式加深學生對奇偶性的理解。

提問：你能說兩個奇數或者偶數嗎？

生說，師板書。板書時兩個偶數、兩個奇數、一奇一偶分別寫三行。

提問：想一想，這幾個數的和分別是奇數還是偶數？

生：兩個奇數的和是偶數，兩個偶數的和是偶數，一奇一偶的和是奇數。

提問：剛才我們對這幾組數的和的奇偶性做了一個猜想，我們的猜想對嗎？

想不想一起探究？這節課我們就來研究和的奇偶性。

【設計意圖】通過說奇數和偶數，給學生判斷奇數和偶數提供更直觀的感受，感受到什么樣的數是奇數或偶數。通過提問，學生對舉例的三組奇數和偶數的和有了判斷，通過這一具體的實例，讓學生去尋找一般規律。

二、自主探究：發現規律

提問：我們研究和的奇偶性，從幾個數開始研究比較好？

生：從兩個數來類推多個數比較好。

【探究活動一】探究兩個數和的奇偶性

活動要求：

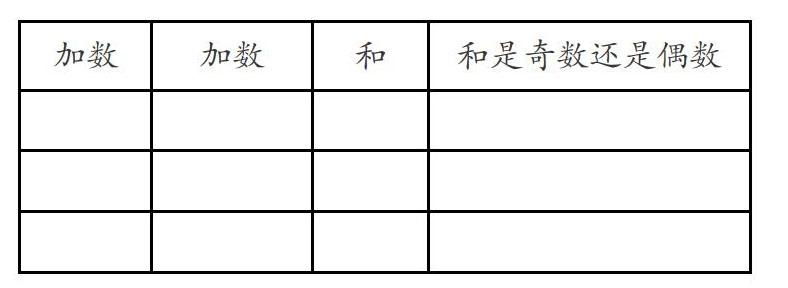
1.計算：任選兩個不是0的自然數，求出它們的和。

2.觀察：它們的和是奇數還是偶數。

3.交流：小組內互相說說你的發現。

[加數 加數 和 和是奇數還是偶數 ]

我的發現：

___________________________________

匯報：學生展示探究結果。

提問：雖然例子不同，但是結論一樣，你的發現是什么？

生1：兩個偶數的和是偶數，兩個奇數的和也是偶數。

生2：一個奇數與一個偶數相加，和還是奇數。

提問：我們的發現對嗎？一起來驗證一下。

驗證：

提問A：打開數學書，左、右兩邊的頁碼的和是奇數還是偶數？

生：因為數學書左右兩邊的頁碼一個是奇數，一個是偶數，所以和是奇數。

提問B：任意兩個相鄰自然數的和呢？你知道這是為什么嗎？

生：這兩個數一個是奇數，一個是偶數，和也是奇數。

提問C：剛才我們通過舉例的方法驗證了我們的發現，現在你能不能用圖形來驗證？

生1：奇數+奇數=偶數，兩個兩個一圈，兩個奇數都會有落單的，兩個落單的可以一圈，全部圈完，都是兩個組合的，說明和是偶數。

生2：偶數+偶數=偶數，兩個兩個一圈，兩個偶數全部圈完，都是兩個組合的，說明和是偶數。

生3：奇數+偶數=奇數，兩個兩個一圈，奇數有一個落單，偶數全部圈完，說明和是奇數。

小結：兩個數相加和的奇偶性是什么？

生：偶數+偶數=偶數;奇數+奇數=偶數;奇數+偶數=奇數。

【設計意圖】這一環節主要通過獨立探究、小組合作探究、班級集體探究來完成，既有獨立的思考空間，又有思維火花的碰撞，集思廣益，思維互補。學生探究兩個數和的奇偶性可以通過舉列、畫圖等多種形式來探究出結果，方法不唯一，讓每一個學生根據自己的經驗，用自己的思維方式自由地開放地去探究、去發現，使獲得的概念更清晰，結論更準確。

提問：剛才我們探究了兩個數和的奇偶性，那么多個數的和是不是也有這樣的規律？你覺得可以分為哪幾種情況來討論？

【探究活動二】探究多個數和的奇偶性

活動要求：

1.任選幾個不是0的自然數，寫成連加算式。（獨立完成）

2.分情況討論，先猜想和是奇數還是偶數，再通過計算驗證。（獨立完成）

3.和是奇數還是偶數，與加數中什么數的個數有關系？（組內交流）

學生獨立探究，師巡視了解學情。

選擇一個小組學生來展示探究成果。

提問：你們小組是怎么探究的，你們的結論是什么？

生1：我先探究加數全是偶數的情況，我發現不論加數中有幾個偶數，和都是偶數。

生2：我探究的是加數全是奇數的情況，當加數中有偶數個奇數，和是奇數;當加數中有奇數個奇數，和是奇數。

生3：我研究的是加數中既有偶數又有奇數的情況，我覺得可以不看偶數的情況，還是只看奇數，如果奇數有奇數個，和是奇數;如果奇數有偶數個，和就是偶數。

提問：他們小組總結得非常好，哪個小組還有其他的表示方法？

生1：加數全是偶數。

生2：加數全是奇數。

生3：加數中有奇數，有偶數。

提問：雖然兩個小組的方法不同，但都正確揭示了多個數和的奇偶性。不管是兩個數和的奇偶性還是多個數和的奇偶性，都由什么決定？

生：都由加數中奇數的個數決定。加數中有奇數個奇數，和就是奇數;加數中有偶數個奇數，和就是偶數。

【設計意圖】這是本節課設計的第二個探究環節，學生在此前剛完成第一個探究，已經有過探究經歷，這里的第二個探究學生應該是輕車熟路。這個探究要求也更加簡化，要求學生用最優化的方法探究出多個數相加的和的奇偶性。學生通過類比的思維方法以及聯想的思維方法，通過舉例計算推出結論，這樣有助于培養學生豐富的想象力和知識遷移能力。

三、鞏固練習：應用規律

問題1：

（1）加數+加數=20，加數+加數=148

提問：兩個加數是奇數還是偶數？

生：兩個加數都是奇數或者都是偶數。

（2）加數+加數=45，加數+加數=517

生：兩個加數一個是奇數一個是偶數。

問題2：1+2+3+4+……+100，和是奇數還是偶數？

生1：這個是高斯求和，和是5050，是偶數。

生2：這是1到100的所有的數相加，有50個偶數，50個奇數，奇數的個數是偶數個，所以和是偶數。

【設計意圖】這是在本節課和的奇偶性已經探究完之后安排的兩個練習，主要是檢驗學生對和的奇偶性掌握情況，第一個問題并沒有正向去考察，而是通過和的奇偶性去判斷加數的奇偶性;第二個問題是通過分析加數的奇偶性去判斷和的奇偶性。一正一反，靈活運用，加深學生對所探究規律的理解。

四、自我評價：課堂梳理

提問：回顧這節課，你有什么收獲？