樂思樂學 彰顯個性
◎羅元景
關注學生質疑可以讓學生體驗成功的喜悅,從而增強自信心。
我在上到北師大版八年級下冊第三章第三節《中心對稱》時,上完新課后,將知識進行拓展。
當在判斷圓、線段、等腰三角形、等邊三角形、平行四邊形等圖形是不是中心對稱圖形時,“熱炒熱賣”,“乘勝追擊”,對平行四邊形作再進一步的探索——如何用一條直線將一個平行四邊形進行面積兩等分,很多學生馬上給出了答案,我也請同學上黑板去畫,“對角線所在的直線”“兩條對邊中點連線所在的直線”共有四種。
我就問“還有嗎?”
部分同學開始搖頭了,但有部分同學想既然老師這樣問可能還有。
于是又開始思索和探討,不斷用直尺進行比劃。
有同學發現,只要對邊左右等距,對邊兩點所在的直線都可以。
這時同學們可熱鬧了,都想來畫出這條直線,我分別請了幾個同學上黑板來畫,但是還是沒發現什么規律,因為是每個平行四邊形同學只畫了一條。
此時,我就問“能將一個平行四邊形面積兩等分的直線有多少條?”
學生整齊回答:“有無數條!”
我緊接著問:“這無數條有什么特點?在同一個平行四邊形中試畫幾條?”
此時,同學們很快發現,這些直線都交于一點,而這一點正好是對角線的交點,所以只要過對角線的交點任意畫一條直線都可以,我利用事先準備好的課件,進行動畫演示,再利用平行四邊形是中心對稱圖形進一步驗證了學生的這一結論。
我接著又問“那么平行四邊形換成長方形和正方形了,情況如何呢?”
同學們很快給出了答案.“與平行四邊形的結論是一樣的”
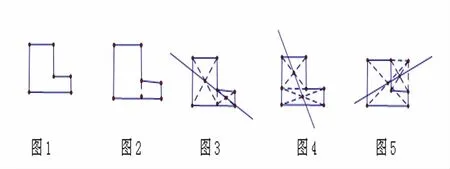
我接著提問:“那如果將矩形的一角挖去一個矩形,成了一個L形圖(圖1),又如何畫一條直線將其分為面積相等的兩部分?”
同學們又開始思考起來,嘗試的有,但正確的卻沒有。
我準備提示時,一個平時不愛說話的小女孩小聲說了,把它分成兩個矩形,(圖2)同學們笑了,怎么可能,分出的矩形一眼就看出一大一小,面積肯定不相等,該同學也尷尬了,臉也涮的一下紅了。
此時,我馬上鎮住了場面,“雖然某同學的這條直線不能將圖形進行面積兩等分,但是卻把原來的圖形分成了兩個矩形,前面說只要過矩形的對角線交點的直線就能將圖形進行兩等分”。
此時有同學舉手了,“老師,畫出的直線肯定過這兩點,兩點確定一條直線,”“過這兩點作一條直線,”同學們在這位同學的提示下嘗試去畫(圖3),果然畫出的直線能將圖形進行面積兩等分,全班釋然了。
“還有沒有其他畫法呢?”這時不是我追問,而是同學追問了。
“將圖形左右分,也可以將圖形上下分”也是同學在作答了。
于是有了(圖4),“那還有沒有呢?”同學又開始追問了,“既然能分割成兩個長方形,我就把它恢復成一個大長方形,此時,也出現了兩個長方形,分別確定兩個長方形的對稱中心,然后連線即得到符合要求的分割線”(圖5)。這堂課就在這一疑一問一思一答中快樂、分享的度過。
此時,我話鋒一轉“剛才有同學還笑某同學,如果沒有她大膽的嘗試,我們還在一個圖形中被困擾,所以學數學,要敢于質疑,敢于嘗試”。
剛才的那位女孩臉上洋溢羞澀的笑容。從這節課后,這位女孩聽課更認真了,發言也積極了,學習數學的興趣更濃了,還經常跑到辦公室來與我探討題目。性格也變外向多了。因此,關注學生的課堂質疑,關注學生個體差異,可以提高學習的積極性.教學過程中,要尊重學生的個體差異,關注學生情感和自信心的建立。提倡解決問題策略的多樣化,發展學生的學習個性,允許出錯,鼓勵創新,特別是對學習有困難的學生,教師要耐心傾聽他們的看法,適時引導,增強其學習的興趣和自信心,對于學有余力的學生,要提供一些材料,引導他們自學。
關注學生課堂質疑,可以引導學生積極參與教學過程,可以組織學生探索,鼓勵學生創新.
因此我認為,在學生不能合適地回答教師的課堂提問時,教師不應隨意地打斷學生的回答,而應傾聽學生的意見,也不要以自己預設的“標準”簡單的否定學生的意見,而應判斷學生的解答是否具有合理的成分并加以恰當的引導。這樣培養出來的學生就不再是簡單的模仿和記憶,而是具有一定創新思維、品格正值、心靈自由的人,這是數學核心素養的目標,也是時代發展的需要。

