一類常微分方程的非標準有限差分法

劉明鼎 段素芳 張艷敏

（青島理工大學琴島學院，山東 青島266106）

微分方程是描述自然科學現象的常用工具，因此對微分方程數值求解的相關理論研究一直是各個領域學者的研究熱點。采用方法也比較多，目前常采用的數值求解方法主要有有限差分法、譜方法、有限元法、小波法、分解法等方法[1-6]。

非標準有限差分法Mickens在1994出版的文獻[7]中進行了詳細地描述。該方法主要討論在構造微分方程的差分格式時，對導數項離散后的分母函數應具有的形式以及非線性項離散后的形式兩個問題。目前國內學者對非標準有限差分方法的應用主要有王媛媛利用非標準有限差分法對Logistic方程進行了分析[8],張磊利用非標準有限差分法和參數擾動法討論了微分方程的求解[9]，秦雯娣討論了幾類偏微分方程非標準有限差分格式解的正性、有界性以及動力學相容性[10]，王倩倩利用非標準有限差分法研究了兩類含空間擴散生物模型數值解并研究了數值解的穩(wěn)態(tài)性[11]。本文將利用非標準有限差分法研究兩類能量守恒振子方程[7]。能量方程在研究物理、流體力學等方面有著重要的作用，例如研究無粘不可壓縮流體以及無粘可壓縮流體的運動現象。

1.一類常微分方程的非標準有限差分格式

在滿足Hamilton原理下構造如下能量方程的非標準有限差分格式

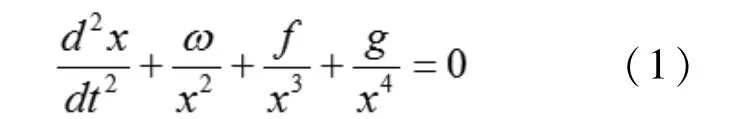
ω,f,g為常數。

首先考慮

構造Lagrange函數[12]

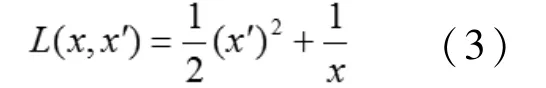
對（3）式在tn處進行離散得：

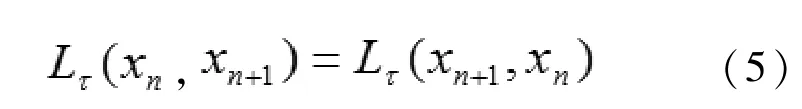
滿足性質[12]

根據式（5）計算得a=b。所以有

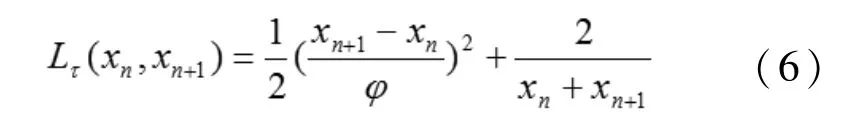
對xn進行移位，利用離散Euler-Lagrange方程[13]，