Helmholtz腔與彈性振子耦合結構帶隙*

2019-05-29 06:25:16陳鑫姚宏趙靜波張帥賀子厚蔣娟娜

物理學報 2019年8期

陳鑫姚宏趙靜波張帥賀子厚蔣娟娜

(空軍工程大學基礎部,西安 710051)

為提高Helmholtz型聲子晶體低頻隔聲性能,設計了一種Helmholtz腔與彈性振子的耦合結構,通過聲壓場及固體振型對其帶隙產生機理進行了詳細分析,建立了相應的彈簧-振子系統等效模型,并采用理論計算和有限元計算兩種方法研究了各結構參數對其帶隙的影響情況.研究表明,該結構可等效為雙自由度系統振動,在低頻范圍內具有兩個帶隙; 在6 cm的尺寸下,其第一帶隙下限可低至24.5 Hz,而同尺寸無彈性振子結構只能達到42.1 Hz,帶隙下限降低了40%,較傳統Helmholtz結構具有更為優良的低頻隔聲特性.另外,在框體尺寸一定的情況下,降低結構間距、增大開口空氣通道長度及振子質量、增大左側腔體體積等方式,是增大帶隙寬度、提高低頻隔聲效果的主要手段.

1 引言

Helmholtz共振腔是一種利用空氣振動的聲學結構,該結構廣泛應用于聲學超表面[1]、聲透鏡[2]及具有負折射[3]、超聲聚焦[4]等效應的聲學超材料構建中.近年來,利用局域共振原理[5]的Helmholtz型聲子晶體成為聲學超材料研究熱點之一[6-8],該類型超材料的典型特點是具有帶隙特性,即在帶隙頻率范圍內的彈性波會在結構中迅速衰減,這為其在隔聲降噪[9-11]等方面的應用奠定了基礎.其中,Guan等[12]通過螺旋設計增加了開口處空氣柱長度,將第一帶隙范圍降至217—492 Hz.劉敏等[13]設計的圓柱形開縫Helmholtz結構打開了100 Hz以下的低頻帶隙.姜久龍等[14]利用雙開口的方式在晶格常數為10 cm的情況下將結構帶隙降至87.1—138.2 Hz頻率范圍內.隨后,Jiang等[15]又通過多腔耦合的方式設計了一種邊長為5 cm的六角形Helmholtz型聲子晶體,該結構帶隙下限低至62.1 Hz.

這些研究對于提高Helmholtz結構隔聲效果具有重要意義,但仍只有空氣參與振動,等效振子質量難以進一步提高,若需進一步降低其帶隙下限,往往需要增大結構尺寸,限制了其在工程上的應用.2016年,Abbad和Ahmed[16]將Helmholtz腔的上下壁換為鈍化薄膜,并研究了其隔聲量相對于傳統結構變化情況.2018年,Zhu等[17]推導了穿孔板與薄膜耦合結構的吸聲系數計算公式,這種耦合結構同時利用了薄膜[18-20]和固/氣結構隔聲特性,取得了良好效果.

本文設計了一種帶彈性振子的Helmholtz型聲子晶體,對其帶隙機理進行了詳細分析,建立了等效模型,在6 cm的腔體尺寸下,將帶隙下限降至24.5 Hz,相比于傳統單腔單開口Helmholtz型聲子晶體,帶隙下限降低了40%,實現了小尺寸控制大波長,擴大了其在工程上的應用范圍.

2 結構設計及其帶隙特性

Helmholtz腔與彈性振子耦合結構橫截面如圖1所示,其晶格常數為a,腔體框架材料為鋼,外邊長為l1,腔壁厚度為b,在腔體右側有“弓”字型的開口,其空氣通道總長度為l2,寬度為s,腔體內部與左框體距離l3處設置一寬度為bs的彈性長桿,并在上下兩端用長hr、寬br的硅橡膠連接至腔體框架上,因本研究中選取橡膠厚度與一般薄膜相比較厚,且預應力的施加一般會導致共振頻率升高,故不施加預應力.在實際應用中,可用外部框架將橡膠夾住長為l1的橡膠板,并在板上粘附金屬質量片.這樣,Helmholtz腔就被彈性振子分為左右兩個腔體.另外,為防止框架的振動模態對帶隙形成機理研究造成干擾,將其設定為固定約束狀態.

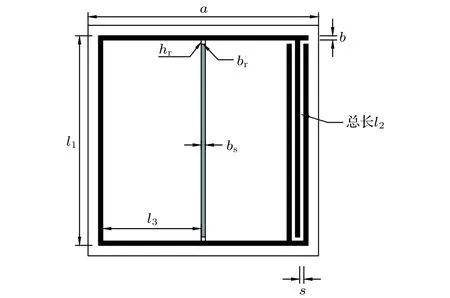
圖1 Helmholtz腔與彈性振子耦合結構橫截面Fig.1.Cross section of Helmholtz resonator coupled with elastic oscillator structure.

將腔體外邊長固定為l1=60 mm,腔壁厚度固定為b=1 mm.先利用理論計算方法對所選參數取值范圍內所有可能組合進行遍歷掃描(均以1 mm為間隔),再利用有限元法進行驗證和調整,分別對Helmholtz腔與彈性振子耦合結構和其對應的傳統Helmholtz腔結構進行求解,其第一帶隙下限最低時的參數組合及各參數取值范圍如表1所列,采用的材料參數列于表2,得出其帶隙結構如圖2(a)所示.

對于傳統Helmholtz腔結構,降低其第一帶隙下限主要通過增大開口長度,由于這樣會使得腔體體積減小,導致其第一帶隙下限最低低至42.1 Hz(如圖2(b)所示).而對于Helmholtz腔與彈性振子耦合結構,其第一、二帶隙分別為24.5—47.7 Hz,237.6—308.6 Hz (如圖2(a)所示).

為探究Helmholtz腔與彈性振子耦合情況下的帶隙機理,設置初始結構參數如表1所列.利用有限單元法得出其帶隙結構如圖3(a)所示,從圖中可以看出,該結構在700 Hz以下存在兩個帶隙,其中第一帶隙為125.34—267.30 Hz,第二帶隙為355.13—397.22 Hz,各帶隙的起止點已在圖中標出.另外,在179.17 Hz和254.69 Hz處出現了兩條平直帶.

為研究該結構的隔聲性能,沿縱向串聯3個元胞結構,在結構的一端設置背景壓力場,并配置完美匹配層(PML),利用聲壓模式的隔聲量計算公式針對0—700 Hz范圍內的聲波進行隔聲量計算：

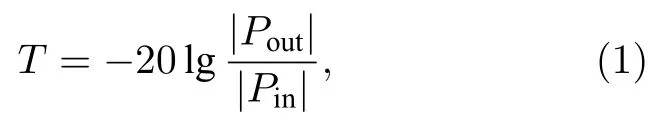
其中T代表隔聲量,Pout代表出射聲壓,Pin代表入射聲壓,其結果如圖3(b)所示.可以看出,兩個隔聲峰均出現在帶隙下限附近,大小分別為43.2和43.3 dB,而兩個平直帶對隔聲曲線無明顯影響.

表1 各結構參數組合Table 1. Combination of various structural parameters.

表2 各材料參數Table 2. Material parameters.

圖2 (a) Helmholtz腔與彈性振子耦合結構帶隙圖; (b) Helmholtz腔結構帶隙圖Fig.2.(a) Band diagram of the Helmholtz resonator coupled with elastic oscillator structure; (b) band diagram of the Helmholtz resonator structure.

圖3 (a) Helmholtz腔與彈性振子耦合結構帶隙圖; (b) Helmholtz腔與彈性振子耦合結構隔聲曲線Fig.3.(a) Band diagram of the Helmholtz resonator coupled with elastic oscillator structure; (b) the transmission spectra of the Helmholtz resonator coupled with elastic oscillator structure.

3 帶隙機理及等效模型

Helmholtz腔與彈性振子耦合結構帶隙上下限處的聲壓場如圖4所示,在A點(模態A),左腔聲壓最大,右腔次之,而腔體外部聲壓為零.表明此時振子與開口中空氣做同向振動,而外部空氣未參與振動,聲波被局域在腔體內部,無法向外傳播,由此形成帶隙下限.

在B點(模態B),左腔聲壓為負值,右腔及腔體外部聲壓為正值且外部聲壓最大.表明此時振子與開口中空氣做同向振動,且聲波可以在腔體外部傳播,由此對應帶隙上限.

C (模態C),D (模態D)兩點處腔體外部聲壓分別與A,B兩點處基本相同,表明其帶隙形成機理是一致的.但C點處左腔聲壓為負值而右腔聲壓最大,表明此處對應振動模態為振子與開口中空氣做相向振動.D點處左右腔聲壓與B點處相比聲壓顛倒,表明此處對應振動模態同樣為振子與開口中空氣做相向振動.

圖4 (a) A點,(b) B點,(c) C點,(d) D點的聲場壓力圖Fig.4.Sound pressure distribution diagrams of point A (a),B (b),C (c),and D (d).

對于平直帶處的振動模態,通過聲壓場和彈性振子的振動模態相結合進行分析,如圖5所示.為便于分析,在聲壓場圖中添加了等值線.

在兩平直帶處,彈性振子的振動分別為繞中心轉動和沿軸向振動,雖然這種振動因流-固耦合作用會使得各腔內聲場發生變化,但因振動過程中左右腔體積均不變,故各腔聲場的變化分別是上下反對稱的(如圖5(c)和圖5(d)所示),其總的等效聲壓為零.此時,彈性振子的振動并不能激發開口處空氣的振動,從而無法將聲壓傳導至腔外,聲波仍然被局域在腔內,故對該結構的隔聲性能沒有影響.這一點也從圖3所示的隔聲曲線上有所體現,平直帶對應的頻率處,隔聲曲線沒有特別的變化特征.

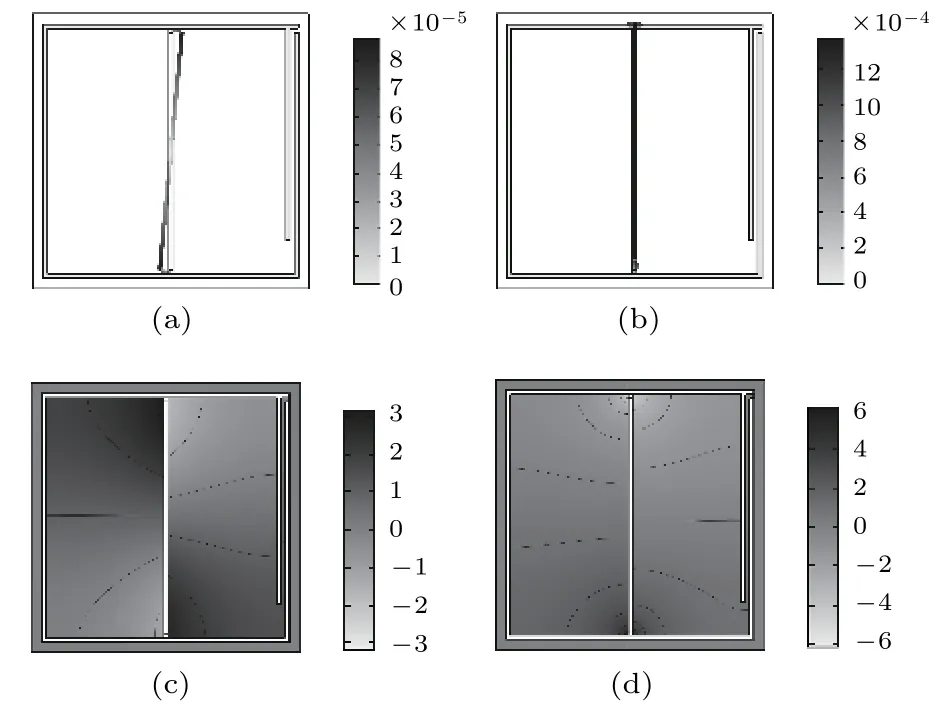
圖5 (a) 第一平直帶彈性振子振型圖; (b) 第二平直帶彈性振子振型圖; (c) 第一平直帶聲場壓力圖; (d) 第二平直帶聲場壓力圖Fig.5.The vibration mode of the elastic oscillatorat the first straight belt (a) and at the second straight belt (b);the sound pressure distribution diagrams of the first straight belt (c),and the second straight belt (d).

對于局域共振型聲子晶體,由于帶隙上下限共振機理不同,其等效模型一般通過彈簧-振子模型[21,22]或聲電類比模型[14,15]對帶隙上下限分別進行構建.在本研究中,選用彈簧-振子模型.首先做如下假設：

1)對于開口處,由于其體積相比內腔小得多,且開口寬度較小,假設開口內空氣做同步運動且不計其受到的壓縮,即視為振子,其等效質量由m2表示;

2)對于左右腔及外部空氣,忽略其振動造成的慣性力,即視為無質量彈簧,其等效剛度分別由k4,k2,k1表示;

3)對于彈性振子,忽略其振動時的撓度變形,將其視為剛性振子(在仿真時仍設定為彈性體),并將兩端橡膠質量通過集中參數法等效分布于振子和腔壁上,其等效質量由m1表示;

4)對于彈性振子兩邊的橡膠,將其考慮為受剪切變形影響的橫向振動無質量伯努利-歐拉梁,忽略自身振型的影響,在模型中用等效剛度為k3的彈簧擬合其特性.

綜上,對該結構各帶隙起止點建立等效模型如圖6所示,其中圖6(a)對應帶隙上限,圖6(b)對應帶隙下限,這兩種等效模型的區別在于是否存在外部空氣等效所得的彈簧k1,這種不同來源于對開口處空氣的簡化.開口空氣實際相當于一縱向振動彈性桿,這與圖4中其聲壓場逐漸變化相對應.該結構更為精確的模型為“彈簧-質量塊-彈簧-彈性桿-彈簧”.但在k1,k2較小且開口長度適中的情況下,可通過假設1)的處理,僅考慮開口空氣質心的振動位移,此時在帶隙上限處將彈性桿視為質量塊即可.但在帶隙下限處,外部空氣聲壓始終為零,即系統在振動過程中,開口空氣桿的外端始終靜止,無法體現彈簧k1的作用,但桿的質心仍在振動,故可簡化為圖6(b)所示的等效模型.

設該結構高度為1,其等效質量和等效剛度的表達式分別為：

圖6 (a) 模態B,D的等效模型; (b) 模態A,C的等效模型Fig.6.(a) The equivalent model of modal B and D; (b) the equivalent model of modal A and C.

其中ρs,ρr及 ρair分別為彈性振子、橡膠及空氣的密度; c為空氣中聲速; V1,V2及V4分別為外部空氣、右腔及左腔的體積.需要說明的是,在多自由度振動理論中,將總的等效剛度定義為“kij是使系統僅在第j個坐標上產生單位位移而相應于第i個坐標上所需施加的力[23]”,而忽略自身質量的空氣彈簧遵循帕斯卡定律,則“所需施加的力”為第j個坐標上產生單位位移引起的壓差對第i個坐標上空氣與構件接觸面積的積分.對于右腔空氣,由于其分別與開口處空氣及梁狀振子接觸,會表現出四種不同的等效剛度,分別為：

k2left,僅開口處空氣產生單位位移時在彈性振子與右腔空氣接觸面上產生的力;

k2right,僅開口處空氣產生單位位移時在開口處空氣與右腔空氣接觸面上產生的力;

k′2left,僅彈性振子產生單位位移時在彈性振子與右腔空氣接觸面上產生的力;

k′2right,僅彈性振子產生單位位移時在開口處空氣與右腔空氣接觸面上產生的力.

k3可由傳遞矩陣法求得,設彈性振子有一位移u,根據橡膠短梁的傳遞矩陣和邊界條件：

對于上下兩橡膠短梁均有

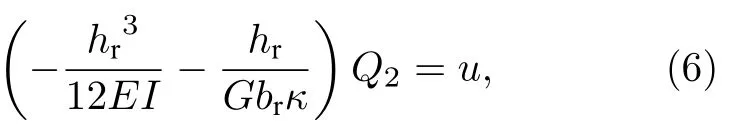
其中E,G分別為橡膠的彈性模量和剪切模量;I為截面慣性矩; κ 為截面系數,取為0.833; M1,Q1,M2,Q2分別為與腔壁相連端及與振子相連端的彎矩和剪力.由此可得出

根據上述兩種等效模型,構建其剛度矩陣分別為：

其質量矩陣為

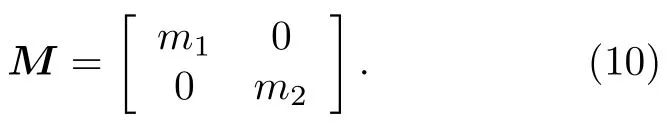
根據多自由度振動理論,由 (8)—(10)式即可分別計算出兩階固有頻率,對應于第一、二帶隙的起止頻率：

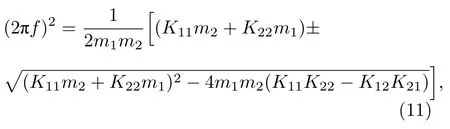
式中Kij代表剛度矩陣(8)和(9)式中各元素.

通過以上分析可以看出,在Helmholtz腔中加入彈性振子之后,系統由單自由度變為雙自由度,且其耦合效應改變了原有腔體的等效剛度.另外,該結構左腔中的空氣和彈性振子局域共振單元一起,形成了一個彈性壁,但其對于外部空氣來說仍為剛性壁,故不能直接對外部空氣起作用,必須通過引起腔口空氣振動而影響外部聲壓.若去除左側框架,則等效模型中m1,m2應與雙開口Helmholtz腔[14]中類似,用并聯設置替代本文中的串聯設置.

4 帶隙影響因素研究

為分析各參數對帶隙的影響,進一步揭示其帶隙形成實質,采用有限單元法和等效模型兩種方法計算了其帶隙上下限頻率隨參數改變的變化情況,結果如圖7所示.

圖7(a)顯示了晶格常數a與一、二帶隙的關系.可以發現,晶格常數的改變對于帶隙下限的影響可以忽略不計,這與(4)式中不含外部空氣的等效剛度一致.而對于帶隙上限,單純增大晶格常數而保持框體大小不變,會直接導致k1的減小,從而使帶隙上限向低頻方向移動.這說明對于該結構,周期性排列間距越小越容易產生較寬的帶隙.

圖7(b)顯示了開口處空氣通道長度l2與一、二帶隙之間的關系,可以看出,隨著空氣通道長度的增加,其帶隙上下限都在下降,其中第一帶隙寬度略有增大,而第二帶隙寬度有較明顯的減小.另外需要指出的是,當空氣通道長度l2較小時,第二帶隙等效模型與有限元分析結果差距較大,這是因為在模態C,D處,開口左右聲壓差值大,導致開口附近空氣受到的壓縮程度更大,更多的空氣充當了振子的作用,使得等效質量m2增大,而這種效應在開口長度較小時尤為明顯.此時,應通過修正公式[24]對m2進行修正,本研究中選取初始開口長度較長,不影響其他討論及最終結論,故不再進行修正.

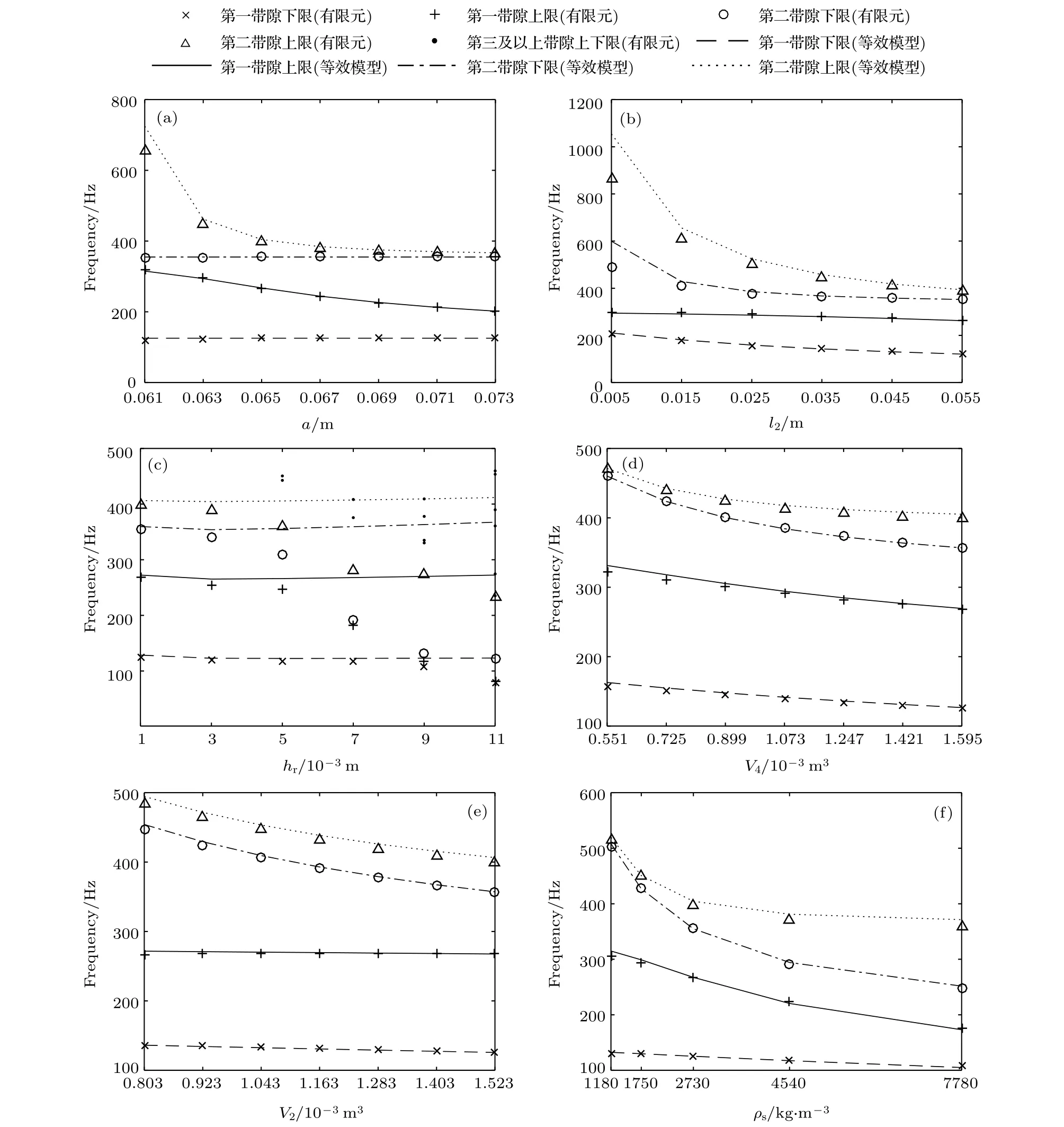
圖7 晶格常數a (a),開口長度l2 (b),左腔體積V2 (d),右腔體積V4 (e),彈性振子密度 ρs (f)對第一、二低頻帶隙的影響; (c) 橡膠長度hr對各低頻帶隙的影響;Fig.7.The impact of different parameters a on first and second low frequency bandgap： (a) The lattice constant a; (b) the length of the cavity opening l2; (d) the volume of the left cavity V2; (e) the volume of the right cavity V4; (c) the impact of the parameter hr on each low frequency bandgap.

圖7(c)顯示了參數hr與帶隙寬度的關系,在圖中繪制了等效模型計算的兩個帶隙和有限元仿真的前6個帶隙(若存在).從圖中可以看出,由等效模型計算的帶隙上下限變化較小,這是因為鋁密度與硅橡膠相差不大,hr的增大只使m2小幅變化,而k3由于與相差一個量級,其變化對結果影響較小.而有限元計算結果顯示,隨著hr的增大,部分特征頻率曲線或在原有帶隙附近產生了寬度較小的新帶隙,或將原有帶隙“分割”為兩個帶隙,并影響了原帶隙上下限.此時,視新帶隙相對原帶隙的位置,有限元計算結果開始在理論計算結果上下波動.

這是由于隨著hr的增大,彈性振子系統振動模態增多,原有各階固有頻率下降,在帶隙上下限處,對應的不再是原有的低階振型,如當hr為1,3,7,11 mm時,第一帶隙下限分別對應于彈性振子系統的第1,2,3,5階振型.此時,將質量和等效彈簧均集中于振子處的處理方法導致了誤差的產生.若要精確計算帶隙上下限,需要參考文獻[25,26]等采用的腔口覆薄膜耦合振動計算方法并推廣至含集中質量結構,充分考慮強迫振動振型對固有頻率的影響.但綜合圖7(c)和圖7(e)可以看出,振型對于帶隙的影響不如彈性振子等效質量的影響大,且振型的影響規律性不強,不利于帶隙的優化,本文不再進行精確計算.

圖7(d)和圖7(e) 表征的是隨V2,V4增大時帶隙的變化情況,由于腔體被彈性振子分為兩部分,為使結構改變時保持k2,k4中的一項不變而另一項增大或減小,在此沒有對l3進行變量分析,而是采用在左腔或右腔中增加剛性填充物的方式進行參數控制.從圖中可以看出,隨著左側腔體體積V4的增大,一、二帶隙上下限均向低頻方向移動,而右側腔體體積V2的增大僅使第二帶隙上下限下降,對第一帶隙的作用并不明顯.這說明在保證左側腔體的一定體積的情況下,降低右側腔體的體積,仍能獲得良好的低頻隔聲性能,有利于結構的小型化; 而在結構大小一定的情況下,則應盡量增大參數l3,以使第一、二帶隙均向低頻方向移動.就產生該現象的機理來看,在第一帶隙上下限處,振子與腔口空氣均做同向振動,故削弱了右腔空氣的作用; 而第二帶隙上下限處振子與腔口空氣做相向運動,故與左右腔空氣體積均有關.

圖7(f)顯示隨著彈性振子密度 ρs的提高,一、二帶隙上下限都向低頻方向移動,但第一帶隙寬度降低,而第二帶隙寬度增大.在這里,為改變其密度,分別選用了環氧樹脂、碳、鋁、鈦、鋼等材料進行研究,因其彈性模量基本處于同一量級,故彈性模量的變化影響可以忽略.綜合圖7(b)和圖7(f)的結果,可以看出,振子質量與開口處空氣質量對于帶隙寬度的作用效果是相反的,開口處空氣質量對應于第一帶隙,而振子質量對應于第二帶隙,增大其中某質量會使其對應帶隙寬度增大而另一帶隙寬度減小.

5 結論