效應量置信區間的原理及其實現

王珺 宋瓊雅 許岳培 賈彬彬 胡傳鵬

摘?要?在心理學可重復危機的背景之下，報告效應量及其置信區間正逐漸成為主流心理學界所要求的新標準，但是研究者可能對效應量的置信區間缺乏足夠的理解。為增強研究者對效應量置信區間的理解及應用，本文介紹了心理學研究中最常用的效應量指標——Cohen's d與η2——置信區間的基本原理，即在備擇假設（H1）為真時，需要通過迭代估計的方式來估計相應非中心分布的非中心分布參數，從而構建Cohen's d與η2的置信區間。其中Cohen's d對應的是非中心t分布;而η2對應的則是非中心F分布。使用現有的計算機程序，能夠對Cohen's d與η2的置信區間進行計算，例如 R與JASP，本文對此進行了分別展示。報告效應量置信區間不僅有助于研究者更好地進行統計推斷，也有利于整個科學界知識的積累，因此本文介紹的方法對研究者具有十分重要的意義。

關鍵詞?效應量;置信區間;Cohen's d;Eta squared;R

分類號?B841.2

DOI： 10.16842/j.cnki.issn2095-5588.2019.05.003

1?引言

統計推斷是研究者根據數據進行邏輯推導從而驗證研究假設的必要手段。虛無假設顯著性檢驗（null hypothesis significance test， NHST）是心理學研究中最為常用的統計推斷手段（Cumming et al.， 2007）。但該方法以p值是否小于0.05作為決定統計顯著性的指標，間接導致了心理學研究的假陽性過高;且p值受抽樣樣本的影響較大，不適合作為重復研究或跨實驗研究比較的統計指標（胡傳鵬， 王非， 過繼成思， 宋夢迪， 隋潔， 彭凱平， 2016）。近年來，隨著對心理學研究可重復性的廣泛關注，NHST的局限性再次引起眾多學者的重視（Kline， 2004; Wagenmakers， Wetzels， Borsboom， & van der Maas， 2011）。為了彌補NHST的不足，新的統計方法開始逐漸被引入心理學研究，例如基于估計的統計（estimates-based statistics）（Cumming， 2012， 2014）、貝葉斯因子（胡傳鵬， 孔祥禎， Wagenmakers， Ly， 彭凱平， 2018; Wagenmakers et al.， 2018）、似然性方法（Etz， 2018）。其中，基于估計的統計方法由于易于理解，且能夠彌補NHST的不足，被國內外研究者推薦。該方法所強調的效應量（effect size）及其置信區間（confidence intervals， CIs）正逐漸成為國際、國內重要心理學期刊論文中必須報告的統計指標（APA Publications Communications Board Working Group on Journal Article Reporting Standards， 2008; Appelbaum， Cooper， Kline， Mayo-Wilson， Nezu， & Rao， 2018; Cumming， 2014）。

盡管如此，相比“統治”了心理學數十年的NHST，效應量及其置信區間在心理學研究中的使用仍十分有限，極少研究報告效應量的置信區間（Fritz， Morris， & Richler， 2012）。國內研究者雖對效應量的概念進行過不少的介紹（胡竹菁， 2010; 盧謝峰， 唐源鴻， 曾凡梅， 2011;鄭昊敏， 溫忠麟， 吳艷， 2011），但卻很少提及效應量的置信區間。

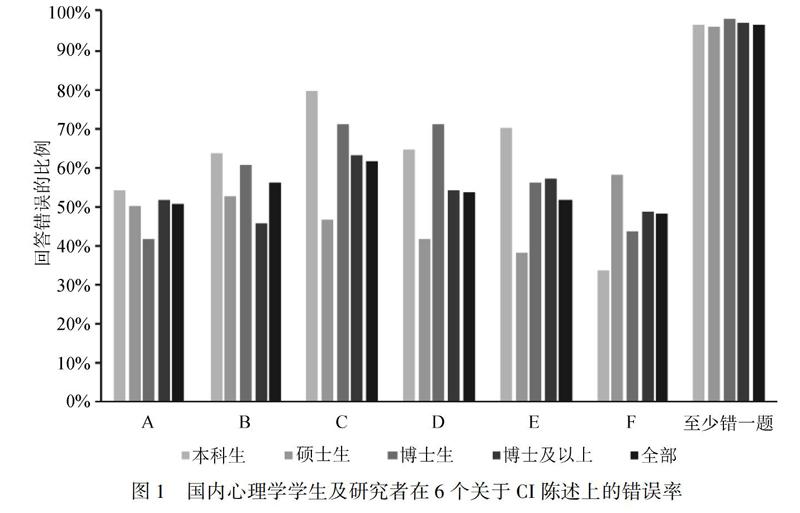
值得注意的是，心理學專業研究人員、學生對置信區間仍有一定誤解（胡傳鵬等， 2016; Hoekstra， Morey， Rouder， & Wagenmakers， 2014）。例如，胡傳鵬等人（2016）針對國內研究者對CI的理解情況進行了調查。在該調查中，呈現一個假想的研究，其效應的95%置信區間為[0.1， 0.4]，受訪者需要判斷是否能夠根據這個置信區間推斷出如下6個陳述：A. 真實的均值大于0的可能性至少是95%;B. 真實的均值等于0的可能性小于5%;C. 真實的均值等于0的“零假設”很可能是不正確的;D. 真實的均值有95%的可能性在0.1和0.4之間;E. 我們有95%的信心認為真實的均值在0.1和0.4之間;F. 如果我們重復該實驗，則95%的時候，真實的均值會在0.1和0.4之間。上述6個陳述均屬于對置信區間的誤解（Hoekstra et al.， 2014），但是大部分受訪者或多或少將其判斷為正確解讀。（見圖1，數據來自Lyu， Peng， & Hu， 2018）。實際上，置信區間的正確解讀應該是，如果不斷重復該實驗并計算置信區間，在所有計算出來的置信區間中，約有95%的置信區間包含真實的均值。因此這里的[0.1，0.4]是理論上眾多置信區間中的一個，其是否包括真值是未知的（Cumming， 2014）。

為加深研究者對效應量及其置信區間的理解，同時便于研究者準確計算和報告效應量及其置信區間，本文首先介紹效應量的置信區間及其優勢，然后以兩種常用的效應量（Cohen's d及Eta squared， η2）為例，介紹其置信區間的原理及如何在開源軟件（如R和JASP）中實現。但值得注意的是，本文提及的效應量并不僅限于Cohen's d等標準化的效應量指標。根據Cumming（2014）的定義，效應量是研究者感興趣的任何效應的量。因此效應量既可以是標準化的，也可以是未標準化的、帶有原始單位的。研究者應根據實際情況，選擇報告那些能夠合理反映數據信息且易于解讀的效應量。

2?報告效應量及其置信區間的優勢

與NHST中的p值相比，報告效應量及其置信區間為結果提供了更詳細、更多元的信息。具體而言，報告效應量及其置信區間有如下優勢：

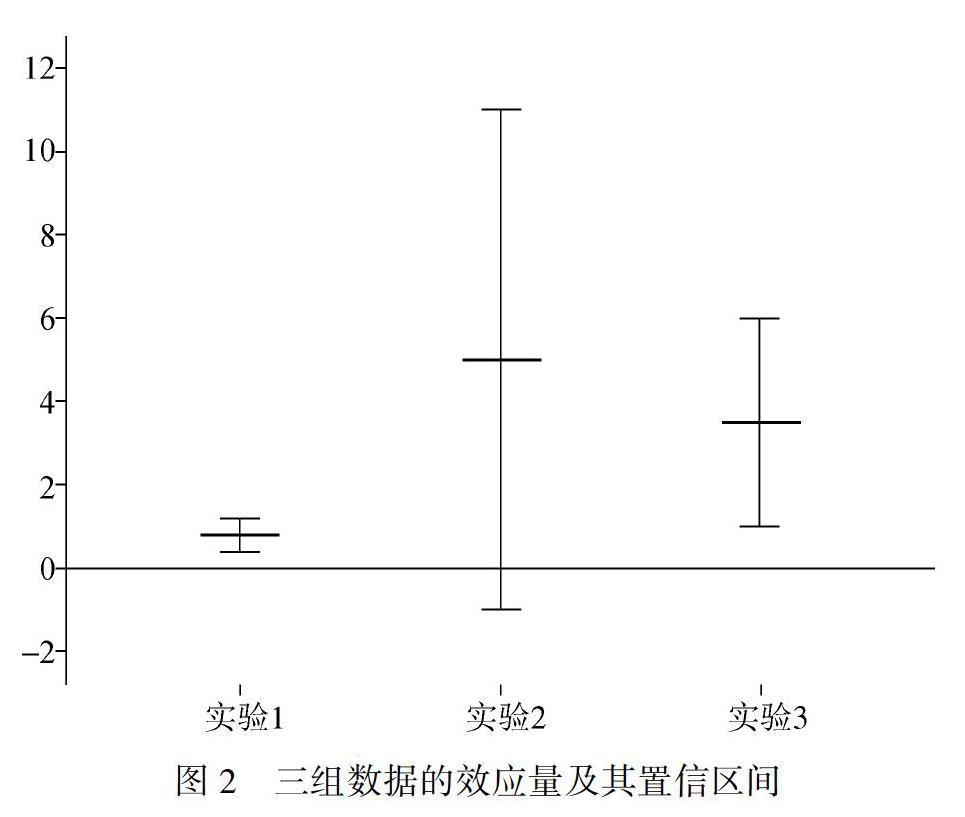
第一，能夠比較不同實驗之間的誤差大小。假如研究者進行了三個實驗，其效應量及置信區間分別如圖2所示。如果根據傳統的NHST方法，研究者能夠得出的結論為：在實驗1和實驗3中，p<0.05，即兩組均值均與0有顯著差異;而實驗2的p值大于0.05，即其均值與0沒有顯著差異。在這種情況下，研究者根據實驗1和實驗3得出的結論幾乎是相同的。至于兩組均值的差異到底有多大？數據的抽樣誤差如何？三組數據哪一組能為假設提供最可靠的證據？p值無法給出答案。

在傳統的報告規范中，研究者通常利用未經標準化的點估計指標（例如：均值）及標準誤來彌補上述不足，同樣的報告效應量（此處為均值差）及其置信區間則能夠達到相同目的。根據圖2可知，實驗1與實驗3雖然均顯著，但是相對而言，實驗1的效應量較小、變異也較小，實驗3則效應量較大，變異也較大。由于對效應量及其置信區間的分析，研究者對實驗1和實驗3的結論就會有所區別。

第二，效應量及其置信區間能幫助研究者得出正確的結論。在僅參考效應量及置信區間的情況下，大部分研究者能夠在比較不同研究的結果時得出符合邏輯的結論;但僅憑NHST和效應量時， 能夠得出正確結論的人數減少（Coulson， Healey， Fidler， & Cumming， 2010; Lyu et al.， 2018）。相比NHST的二分思想，報告效應量及其置信區間將研究者引向一種“估計”“定量”的取向（Cumming & Fidler， 2009）。在這種思維取向下，研究者也更傾向于提出量化的問題。仍以圖2為例，實驗2的結果雖然不顯著，但是從效應量及其置信區間上來看，該實驗的趨勢與實驗1和實驗3是相同的。這也使得研究者對研究產生進一步深化的思考。例如，是否是實驗2中數據的“噪音”過大導致了不顯著的結果？

第三，可以展現關于研究更豐富的信息。在圖2中，實驗1的效應量其實很小，換言之實驗1中的兩組實際差異可能不大。但是也許由于實驗抽樣誤差小、樣本量較大，實驗1的置信區間很窄，研究者可以在很高的置信水平上得到差異顯著的結論。這就是統計顯著性與實際顯著性不相稱的實例。與之相反，對于實驗2，雖然其置信區間包含0，但其效應量的點估計值卻是最高的，由此可見在實驗2數據的“噪音”過大，導致了其數據變異過大、置信區間過寬。實驗3的結果則較為理想，其效應量及其置信區間都在較為合理的水平。

第四，由于效應量從理論上講不依賴于樣本的大小（盧謝峰等， 2011），相比依賴樣本的p值，它更適用于跨實驗的綜合分析及元分析研究中。從頻率主義統計的角度來講，任何一個單獨的研究可以看作是進行一次獨立的抽樣并對總體的參數進行一次估計，因此單個的研究很可能是片面的，但通過多個研究的數據積累，研究者可以通過元分析（meta-analysis）對總體進行更加精確地估計。元分析不僅能擴大樣本量，提高統計檢驗力，還可以縮小置信區間的范圍， 使得對總體效應量的估計更加精確（Cumming， 2012）。相比p值，效應量及其置信區間的研究更便于進行元分析統計，且定量報告效應量及其置信區間的過程本身也蘊含了元分析思想。

正是由于效應量與置信區間的優勢，其得到了研究者的廣泛推薦。在美國心理學會（American Psychological Association， APA）出版手冊（第六版）中，推薦了報告效應量及其置信區間。而在2018年《美國心理學家》（American Psychologist）所介紹的期刊報告標準中，也推薦報告效應量及其置信區間（Appelbaum et al.， 2018）。

總之，在當前的研究中，雖然報告效應量及其置信區間得到了廣泛的支持，但是效應量的置信區間卻應用較少（Fritz et al.， 2012）。一個主要的原因可能在于研究者都對效應量的置信區間知之不多，而且缺乏相應的工具進行實現（例如心理學常用的統計軟件SPSS并沒有常用效應量指標的置信區間輸出）。為了解決這個問題，接下來，本文將以Cohen's d和Eta squared（η2）為例，介紹其置信區間的原理與計算公式，并展示如何使用開源的軟件來實現置信區間的計算。

3?標準化的差異量（Cohen's d）

Cohen最早對d的定義是以總體的標準差為標準化單位，然而在實際研究中總體的標準差常常是未知的，因此更常見的做法是使用樣本的標準差作為標準化單位（后文以樣本標準差s為單位進行描述）。Cohen's d的原理即為樣本的均值和虛無假設（H0）的均值差異除以標準差的比值：

其中，s表示樣本的標準差，μ表示我們希望用來測量d的參考值。Cohen's d就可以簡單理解為樣本均值與參考值μ之間相差幾個標準差s。不過，對比不同的研究目的，關于Cohen's d的計算公式有多種形式，具體可以參考Cumming（2014）， Hedges（1981）和Lakens（2013）。

3.1?Cohen's d置信區間的原理

要理解Cohen's d的置信區間，首先需要理解t值在虛無假設（null hypothesis，H0）為真（即沒有效應）和備擇假設（alternative hypothesis，H1）為真這兩種情況下的分布。假設從一個正態分布（N（μ，δ））中隨機抽取無數個樣本量為N的樣本。對于其中的一個樣本，其均數為M，標準差為s。如果想檢驗這個樣本是否屬于標準正態分布的總體，在NHST的框架下，我們可以基于虛無假設H0： μ=μ0進行單樣本t檢驗，可以通過如下公式計算t值：

在虛無假設為真的情況下，假如我們無數次進行抽取樣本量為N的樣本并進行t檢驗，那么這些t值會形成一個自由度df=（N-1）的t分布。在這種情況下，t分布是以0為中心，兩邊對稱的分布。此時，我們也可以將t檢驗的統計量看作是M與μ之間以s/N（標準誤）為單位的距離。對于每一個樣本，我們都可以使用t分布表計算p值，并進行假設檢驗。

但是，如果虛無假設（H0）不為真，那么備擇假設（H1）即為真，即μ=μ1（μ1≠μ0）。在這種情況下，我們實際上是從均值為μ1的總體中進行抽樣，那么無數次抽取樣本量為N的樣本而計算出來的均值M就會更加接近μ1而非μ0。如果仍用上面的公式進行t檢驗，那么無數次計算到的t值不再是以0為中心兩側對稱的t分布，而是中心不在零點的偏態的非中心t分布。對于這樣一個非中心t分布，其參數除了自由度（df）外，還包括一個非中心參數Δ（讀為：delta），Δ可以看作是μ0和μ1之間以標準誤為單位的距離。在其他條件相同的情況下，Δ值越大，說明這個非中心t分布的中心越偏離0（如圖3所示，其中非中心參數ncp表示R軟件中Δ的取值）。

將公式（3.1）和公式（3.2）結合，可以得出

公式（3.1）說明d表示M與μ之間以s（即標準差）為單位的距離;公式（3.2）說明t表示M與μ之間以s/N（即標準誤）為單位的距離。公式（3.3）則表明，Cohen's d與t值有一一對應關系。因此，Cohen's d的抽樣分布也是非中心t分布，在計算Cohen's d的置信區間時需要用到非中心t分布。

由于t值在備擇假設（H1）為真時為非中心t分布，這種情況下d也是一個非中心t分布。也就是說d的置信區間是一個非對稱的區間，上下限到中心的距離不一致，所以我們需要用迭代估計（iterative approximations）的方法來構建d的置信區間。我們可以結合下圖來詳細說明。

假如有一個總體效應為Cohen's d=1.21，需要構建其95%的置信區間（如圖4所示）。也就是說，如果無數次構建這樣的區間，約有95%的區間包含1.21。那么，以區間的下限dL為中心時，d的抽樣分布拒絕dL而選擇真值的概率為 2.5%（x軸上1.21右側的陰影部分）;同時，對于以置信區間上限dU為中心時，d的抽樣分布拒絕dU而選擇真值的概率同樣為2.5%（x軸上1.21左側的陰影部分）。這就意味著，區間的上限和下限為中心的分布包含真值的可能性之和正好為5%;而將區間下限或者上限向中心移動時，包含真值的可能性變大。同理，如果需要估計99%置信區間的范圍，相比于95%的置信區間，區間的上限和下限會更遠離中心，區間的上限和下限為中心的分布包含真值的可能性之和為1%，那么x軸上陰影部分應該是0.005。

Exploratory Software for Confidence Intervals（ESCI）是由Geoff Cumming 設計開發的一系列Excel文件，可以僅僅依托我們常用的Microsoft Excel軟件完成復雜的統計計算，這其中包括效應量Cohen's d及其置信區間（Cumming， 2001）。使用ESCI可以更加直觀地理解區間上限與下限與d值的關系。在ESCI中，將以區間下限dL為中心的分布往左移動，dL就會變小，該分布右側超過真值的區域也會變小;這意味著真值所對應的p值也會變小，那么能夠拒絕dL選擇真值的概率就會變小。同樣的，如果將以區間下限dL為中心的分布往右移動，那么dL值就會變大，該分布右側超過真值的區域就會變大，那么能夠拒絕dL選擇真值的概率就會變大。為了能得到一個準確的95%的置信區間，我們需要移動以dL為中心的分布使得它右側超過d值的區域為0.025，同時移動以dU為中心的分布，使得其左側超d值的區域也為0.025。這樣得到的dL和dU就是我們需要的置信區間的上下限。

因為這兩個曲線都是非中心t分布，所以我們可以改變d值來調整曲線向左右滑動。這種不斷地調整以達到我們需要的區間的方法，即為迭代估計。簡單來說就是在保持自由度不變的情況，通過代入不同的非中心參數Δ（在一些研究中也會寫作δ）進行相應的計算，并進行下一步的調整。在計算置信區間時，不斷地調整Δ，從而不斷調整非中心t分布的位置，使得我們得到的在曲線上的臨界值正好在0.025和0.975的雙尾范圍之間，這樣我們就得到了Cohen's d的置信區間。那么，我們應該如何確定分別以置信區間上限和下限為中心的分布的非中心參數呢？

對于單樣本的研究，非中心參數Δ的計算公式為

關于Cohen's d置信區間的原理，更多細節可參考Cumming（2012） 第11章。

3.2?實例與軟件分析

在研究實踐中，研究者不需要自己進行迭代來估計Cohen's d的置信區間。目前，R語言（R Core Team， 2018）中有不少成熟的工具包可以用于計算Cohen's d的置信區間。而JASP是基于R所開發的用戶界面友好的軟件可以進行傳統的統計分析和貝葉斯因子分析（胡傳鵬等， 2018;

Wagenmakers et al.， 2015），也可以實現Cohen's d的置信區間的計算。（關于SPSS中計算Cohen's d置信區間的插件，見：http：//dl.dropbox.com/u/1857674/CIstuff/CI.html; 基于Microsoft Excel所開發的ESCI計算Cohen's d置信區間， 見： https：//thenewstatistics.com/itns/esci。）

我們將使用JASP示例數據“Kitchen Rolls”（具體數據，見：https：//osf.io/q9387/） 進行說明。Topolinski和Sparenberg（2012）發現，轉動紙卷的方向能夠改變個體在人格量表上開放性的得分，Wagenmakers等（2015）對此實驗進行重復實驗，這里使用的數據即為Wagenmakers等（2015）的重復實驗數據。該示例數據包含兩組被試在人格量表中關于開放性的得分，其中一組被試在填寫問卷時順時針旋轉桌面上的紙卷，而另一組則逆時針旋轉。數據分析中，NEO PI-R的平均得分作為因變量，被試的分組（順時針或逆時針）為自變量，采用獨立樣本t檢驗進行數據分析。

3.2.1?使用JASP計算Cohen's d的置信區間

將樣例數據使用JASP打開后，選擇T-Tests → Independent Samples T-Test， 得到如下界面。根據要求將需要統計的變量導入對應變量框中（與SPSS類似），在下方界面點選需要進行的統計操作，其中在Additional Statistics下可以勾選Effect Size和Confidence interval的選項，根據公式（3.5）-（3.8）計算結果即為效應量Cohen's d及其置信區間。

結果顯示因變量滿足正態分布和方差齊性假設，因此選擇Student t test進行分析。結果顯示兩組的NEO PI-R的平均得分沒有顯著差異（t（100）=0.754，p=0.453），Cohen's d=0.149， 95% CI=[-0.240， 0.538]。

3.2.2?使用R計算Cohen's d的置信區間

R語言中有多個工具包可以完成獨立樣本t檢驗，如car和MBESS。假如我們使用car工具包上的t.test函數，得到兩組被試在NEO PI-R的平均得分沒有顯著差異，t（100）=0.754，p=0.453（當然，也可以使用JASP或者SPSS得到t值與p值）。在得到t值之后，則可通過使用如下命令來計算Cohen's d的置信區間，R代碼如下：

library（“MBESS”） # 打開MBESS工具包

#定義相關參數并計算Cohen's d的95%置信區間

MBESS：： ci.smd（ncp=0.75361， n.1=48， n.2=54， conf.level=0.95）

其中ncp（非中心參數）是t值，n.1和n.2代表兩組的樣本量，MBESS采用公式（3.5）-（3.8）通過運行程序可以獲得結果。

3.3?結果報告與解釋

如上所示，使用兩種不同的軟件對于順時針旋轉組的被試與逆時針旋轉組的被試的人格量表得分差異進行估計，并且得到了95%的置信區間。輸出的結果都表明，兩組被試的NEO PI-R的平均得分沒有顯著差異，對于效應量及其95%的置信區間的估計也是相同的——效應量d為0.149，其95%置信區間為[-0.240， 0.538]。基于這些結果，我們可以得到的結論：目前的數據無法拒絕零假設，即無法推斷出被試進行順時針旋轉或者逆時針旋轉對于NEO PI-R的得分存在顯著影響的。（注意，這里p>0.05及Cohen's d的置信區間包含0均無法得到零假設為真的結論，即無法使用p值來支持兩組沒有差異的結論，因為p值的計算是以零假設為真作為前提條件的。要為零假設為真這個結論提供證據，需要借助其他的統計手段。）

4?方差分析中效應量及其置信區間

心理學研究中另一個最為常見的效應量指標是方差分析（analysis of variance， ANOVA）中的Eta-squared（η2）（Fritz et al.， 2012），其最早由Pearson（1905）提出，可以理解為單個或者多個因素（交互作用）引起的變異在總變異中所占的比例（Cohen & Cohen， 2010）。η2的計算公式如下：

非常值得注意的是，SPSS輸出的效應量指標ηp2在心理學研究中應用廣泛，但是意義與η2不完全相同并且容易引起誤解。例如有研究指出很多研究者很容易混淆η2和ηp2，這種混淆可能會造成一些比較嚴重的后果，如在元分析（meta-analysis）中如果錯誤的使用ηp2代替η2，會使得元分析結果出現嚴重的偏差（Levine & Hullett， 2002）。此外誤用η2和ηp2對理論的建構也十分不利（Pierce， Block， & Aguinis， 2004）。因此報告ηp2的時候一定要注明報告的是哪個指標（對論文中η2與ηp2不明確情況下，可對各個影響因素的效應量相加，一般結果等于1的情況下是η2 ，如果結果大于1，則是ηp2）。另外在樣本量比較小的時候（自變量和樣本的比值小于1∶10），ω2則成為研究者更為推薦報告的效應量指標（盧謝峰等， 2011）。當然與ω2類似的效應量統計指標還有ε2（詳見Maxwell & Delaney， 2018）。下面結合公式4.1主要對η2置信區間計算進行說明。

4.1?η2置信區間計算的原理

要理解η2的置信區間，同樣需要理解與其相關參數有關的非中心性分布。在這里，η2置信區間的建構需要方差分析中F值的分布以及方差分析中另一個效應量指標Cohen's f。以最簡單的單因素被試間設計方差分析為例，其總體變異可以被分解成為組間變異和組內變異：

這是一個自由度為k-1的χ2分布，且這個χ2分布是中心性的（注意，這里的中心性并非指的是該分布是中心對稱，而是說其是從中心對稱的分布中抽出來的數據的平方和的分布）。對照之前方差分析中F值的計算公式，如果將分子和分母同時除以σ2between（處理引起的變異）和σ2error（誤差引起的變異）（在ANOVA的H0為真的情況下，假設處理變異同誤差引起的變異相同即σ2between=σ2error，所以在公式中相互抵消了），則F值（F（df1，df2），以下簡寫為F）的分子和分母分別對應一個χ2分布。

在ANOVA中，由虛無假設為組間均數相等，實驗誤差服從正態分布N（0，σerror）可知，此時的分子分母對應的χ2分布是中心性。在此類情況下，F分布也呈中心性。

當虛無假設為假時，組間均數不相等，分子對應的χ2分布呈非中心性，分母作為實驗誤差對應的分布還是中心性的χ2分布。此時的F分布也變成了非中心性的，可以表示為F（df1，df2， δ）。實際上，中心分布是非中心分布的特殊情況。非中心參數ncp決定了分布的具體形態，例如中心F（2， 52， ncp=0）分布（更高的曲線）和非中心F（2， 52， ncp=1）分布（更矮的曲線），如下圖所示。

計算效應量的前提就是承認H0為假（組間均數不相等），其對應的F分布是非中心分布。如果計算η2的置信區間是基于非中心F分布，則其區間估計的上下限過程中，存在與Cohen's d置信區間估計過程中同樣的問題：在置信區間的上限與下限位置的F分布的非中心參數不相同。因此，對于η2的置信區間的估計，同樣需要使用反演原理（inversion confidence interval principle）（Steiger & Fouladi， 1997）。

我們通過三個階段得到置信區間：統計檢驗→非中心參數→效應量統計。首先我們需要建立統計檢驗值（方差分析下的F值）和非中心參數以及效應量η2之間的關系。由公式4.3可得，因此，可以推出

當虛無假設為假時，F（df1，df2）的非中心參數的估計值δ（非中心參數的符號表達方式可能會有不同，常用的符號包括δ、λ）的計算公式如下（Smithson， 2001）：

結合公式（4.5），我們得到非中心參數的估計：

至此我們建立起了統計值F和非中心參數之間的關系。再綜合公式（4.2），（4.3）和（4.7），可以推斷出η2和f2與非中心參數δ的關系如下：

至此，我們得到了η2與F值、F分布的非中心參數之間的關系。接下來，我們就可以使用置信區間反演原理來計算η2的置信區間。假設給定我們一個樣本F（5，194），我們需要構建一個100（1-α）%（α=0.05）的雙側的置信區間（如圖7所示）。

下限對應F（5，194）右側的α/2處，上限對應F（5，194）左側的α/2處。在得到與上下限對應的非中心參數δ后，我們可以將其轉換為η2的置信區間，轉換公式如下：

這樣我們就完成了對η2的置信區間的估計。

值得注意的是，對ANOVA效應量置信區間的計算，通常報告90%的置信區間即可。原因在于均值之間的差異可以是正值也可以是負值，但是由于η2或R2是平方值，所以只有正值。計算95%的置信區間時，可能會得到包含0的置信區間，但此時p值可能小于0.05，此時置信區間的結果與p值出現了矛盾（見Karl Wuensch的解釋：http：//core.ecu.edu/psyc/wuenschk/spss/spss-programs.htm）。而且Steiger（2004）指出均值比較的95%置信區間和90%置信區間得到的檢驗效力是一樣的，并且η2不可能小于0，所以與0不存在顯著差異的置信區間（通常情況下不包含0）的下限至少要從0開始（Steiger， 2004）。

4.2?η2及其置信區間在R上的實現

同樣，我們將采用由JASP提供的樣例數據來演示如何使用R計算η2的90%CI。該數據名為Tooth Growth和Bugs，分別用來展示被試間設計和被試內設計方差分析中η2及其CI的實現（在SPSS上如何實現， 見： http：//core.ecu.edu/psyc/wuenschk/spss/spss-programs.htm）。

4.2.1?被試間設計η2及其置信區間在R上的實現

Tooth Growth數據來自兩因素完全隨機設計，60只豚鼠被隨機分配到6種處理條件下，用以研究不同類型的營養品（維生素C即VC和橙汁OJ）在不同抗壞血酸劑量條件下（0.5mg、1mg和2mg）對豚鼠牙齒生長的影響，因變量選取的是豚鼠牙齒的長度。

首先使用統計軟件獲得計算置信區間所需的統計值。這里你可以使用R中自帶的函數aov或者一些帶統計功能的工具包（如ez、car等等），這里需要注意的是用R進行方差分析時，不同的工具包或者函數使用的平方和類型會有所不同，例如aov函數進行計算的時候默認使用的是Type I SS（sun of square），ezANOVA默認使用的是Type II SS（可以在R中使用type對平方和類型進行調整，詳見https：//cran.r-project.org/web/packages/ez/ez.pdf），而SPSS在進行方差分析計算的時候默認的是Type III SS（可以在SPSS中模型選項進行調整）。當數據不同組間的被試量相同時，不同類型平方和計算結果出現的差異不大，但是當數據不平衡的時候，則要謹慎考慮平方和類型，因為不同的平方和類型會帶來不同的統計結果（可參考Langsrud， 2003）。當然更為便捷的辦法是應用JASP直接進行統計分析并獲得相應的統計值。例如對于以上數據，可得F（2，54）=92，隨后在R中下載并打開MBESS工具包，輸入相關的統計值進行置信區間的計算，R中的命令如下：

library（“MBESS”） # 打開MBESS工具包

ci.pvaf（F.value=92，df.1=2，df..2=54，N=60，conf.level=0.90） # 輸入F值、自由度計算對應的90%置信區間

4.2.2?被試內設計η2及其置信區間在R上的實現

Bugs數據來自兩因素混合設計，用以研究不同性別（男、女）人群對于不同類型（不嚇人不惡心、不嚇人很惡心、很嚇人不惡心和很嚇人很惡心）蟲子圖片的敵意指數，并采用10點評分表明想要殺死或者驅趕蟲子的程度（Ryan， Wilde， & Crist， 2013）。通過JASP， 我們可以得到F（2.64， 224.48）（注意被試內設計數據在違背球形假設的情況下使用校正后的自由度），然后在R中使用如下命令得到置信區間：

# 打開MBESS工具包

library（“MBESS”）

# 輸入F值及自由度

Lims<-conf.limits.ncf（F.value=20.14，conf.level=0.90，df.1=2.64，df.2=224.48）

# 計算90%置信區間的下限

Lower.lim<-LimsMYMLower.Limit/（LimsMYM Lower.Limit+df.1+df.2+1）

# 計算 90%置信區間的上限

Upper.lim<-LimsMYMUpper.Limit/（LimsMYMUpper.Limit+df.1+df.2+1）

4.3?結果報告與解釋

對于η2及其置信區間的解釋主要參照η2的定義，也就是實驗效應引起的變異占總體變異的比例，因此η2的大小說明了在具體的實驗研究中對于自變量操作的有效性。也就是說η2越大，相關變量之間的關系越緊密，當然這種關系的屬性，即相關還是因果關系主要由實驗設計的類型（如準實驗設計和實驗設計）決定。但是由于η2置信區間不可能小于0，這也就決定了對于η2的解釋不可能像前面提到的Cohen's d的置信區間一樣，把包含0的置信區間作為我們拒絕或者接受零假設的依據。而且方差分析的應用作為一般線性模型下的特例，往往只是對涉及變量間關系檢驗的第一步。因此我們一般把η2及其置信區間作為評價實驗變量操控有效性的指標，接下來具體的組間比較才是研究者關注的重點（例如主效應顯著后的多重比較、交互作用顯著后的簡單效應分析），而在組間比較中可以再次使用如t檢驗下的Cohen's d作為評價組間差異可靠性的效應量指標。

5?總結

近年來心理學中的可重復危機已經對心理學界產生了深遠的影響，而統計報告標準的變化，組成了期刊論文報告標準變化中非常重要的部分（劉宇等， 2018; Appelbaum et al.， 2018; Levitt， Bamberg， Creswell， Frost， Josselson， & Suárez-Orozco， 2018）。Cohen's d與η2作為基于估計統計中兩個最常用的效應量指標，對于研究者來說具有重要意義（Fritz et al.， 2012）。本文解釋了這兩個效應量置信區間的原理，并采用實例演示了如何在R與JASP中實現這兩種置信區間（所有演示數據與代碼，見：https：//osf.io/4ameb/），可能對研究者具有一定的幫助。雖然本文未對另一個常見的效應量指標——相關系數的置信區間也進行說明及演示，但是其計算與實現在JASP與R中均相對成熟，讀者可以參閱相關資料（更多關于置信區間的原理，可見Smithson， 2003）。

值得注意的是，任何一個統計方法均有其優缺點（Rouder， Morey， Verhagen， Province， & Wagenmakers， 2016）。對于心理科學而言，任何新的統計方法都不足以解決可重復危機（胡傳鵬等， 2016; 劉佳， 霍涌泉， 陳文博， 解詩薇， 王靜， 2018）。對于研究者以及整個領域來說，最重要的是充分理解各個統計方法的前提及其不足，否則難以真正避免假陽性。本文所介紹的內容，可能可以幫助研究者達到新報告標準的要求，在結果中提供更豐富的信息。

參考文獻

胡傳鵬， 孔祥禎， Wagenmakers， E. -J.， Ly， A.， 彭凱平（2018）. 貝葉斯因子及其在JASP中的實現. 心理科學進展， 26（6）， 951-965.

胡傳鵬， 王非， 過繼成思， 宋夢迪， 隋潔， 彭凱平（2016）. 心理學研究中的可重復性問題：從危機到契機. 心理科學進展， 24（9）， 1504-1518.

胡竹菁（2010）. 平均數差異顯著性檢驗統計檢驗力和效果大小的估計原理與方法. 心理學探新， 30（1）， 68-73.

劉佳， 霍涌泉， 陳文博， 解詩薇， 王靜（2018）. 心理學研究的可重復性“危機”： 一些積極應對策略. 心理學探新， 38（1）， 86-90.

劉宇， 陳樹銓， 樊富珉， 邸新， 范會勇， 封春亮， ...胡傳鵬（2018）. 心理研究的元分析報告標準：現狀與建議. ChinaXiv. Retrieved from http：//www. chinaxiv. org/abs/201809. 00177

盧謝峰， 唐源鴻， 曾凡梅（2011）. 效應量：估計、報告和解釋. 心理學探新， 31（3）， 260-264.

鄭昊敏， 溫忠麟， 吳艷（2011）. 心理學常用效應量的選用與分析. 心理科學進展， 19（12）， 1868-1878.

Appelbaum， M.， Cooper， H.， Kline， R. B.， Mayo-Wilson， E.， Nezu， A. M.， & Rao， S. M.（2018）. Journal article reporting standards for quantitative research in psychology： The APA Publications and Communications Board task force report. American Psychologist， 73（1）， 3-25.

Cohen， J.（1973）. Eta-squared and partial eta-squared in fixed factor ANOVA designs. Educational & Psychological Measurement， 33（1）， 107-112.

Cohen， J.， & Cohen， P.（2010）. Applied multiple regression/correlation analysis for the behavioral sciences. Journal of the Royal Statistical Society， 52（4）， 691-691.

Coulson， M.， Healey， M.， Fidler， F.， & Cumming， G.（2010）. Confidence intervals permit， but don't guarantee， better inference than statistical significance testing. Frontiers in Psychology， 1：26.

Cumming， G.（2001）. Project design and achieving educational change： from Statplay to ESCI. Melbourne： Biomedical Multimedia Unit， The University of Melbourne，

Cumming， G.（2012）. Understanding the new statistics： effect sizes， confidence intervals， and meta-analysis. New York： Routledge.

Cumming， G.（2014）. The New Statistics： Why and how. Psychological Science， 25（1）， 7-29.

Cumming， G.， & Fidler， F.（2009）. Confidence intervals： Better answers to better questions. Zeitschrift für Psychologie/Journal of Psychology， 217（1）， 15-26.

Cumming， G.， Fidler， F.， Leonard， M.， Kalinowski， P.， Christiansen， A.， Kleinig， A.， ...Wilson， S.（2007）. Statistical reform in psychology： Is anything changing？Psychological Science， 18（3）， 230-232.

Etz， A.（2018）. Introduction to the concept of likelihood and its applications. Advances in Methods and Practices in Psychological Science， 1（1）， 60-69.

Fritz， C. O.， Morris， P. E.， & Richler， J. J.（2012）. Effect size estimates： current use， calculations， and interpretation. Journal of Experimental Psychology： General， 141（1）， 2-18.

Hedges， L. V.（1981）. Distribution Theory for Glass's Estimator of Effect Size and Related Estimators. Journal of Educational Statistics， 6（2）， 107-128.

Hoekstra， R.， Morey， R. D.， Rouder， J. N.， & Wagenmakers， E. J.（2014）. Robust misinterpretation of confidence intervals. Psychonomic Bulletin Review， 21（5）， 1157-1164.

Kline， R. B.（2004）. Beyond significance testing： Reforming data analysis methods in behavioral research. Washington， DC： American Psychological Association.

Lakens， D.（2013）. Calculating and reporting effect sizes to facilitate cumulative science： a practical primer for t-tests and ANOVAs. Frontiers in Psychology， 4： 863.

Langsrud， .（2003）. ANOVA for unbalanced data： Use Type II instead of Type III sums of squares. Statistics & Computing， 13（2）， 163-167.

Levine， T. R.， & Hullett， C. R.（2002）. Eta Squared， Partial Eta Squared， and Misreporting of Effect Size in Communication Research. Human Communication Research， 28（4）， 612-625.

Levitt， H. M.， Bamberg， M.， Creswell， J. W.， Frost， D. M.， Josselson， R.， & Suárez-Orozco， C.（2018）. Journal article reporting standards for qualitative primary， qualitative meta-analytic， and mixed methods research in psychology： The APA Publications and Communications Board task force report. American Psychologist， 73（1）， 26-46.

Lyu， Z.， Peng， K.， & Hu， C. P.（2018）. P-value， Confidence Intervals and Statistical Inference： A New Dataset of Misinterpretation. Frontiers in Psychology， 9：868.

Maxwell， S. E.， & Delaney， H. D.（2018）. Designing experiments and analyzing data： a model comparison perspective. New York： Routledge.

Pearson， K.（1905）. Mathematical contributions to the theory of evolution： XIV. On the general theory of skew correlations and nonlinear regression（Draper's Company Research Memoirs， Biometric Series II）. London： Dulau.

Pedhazur， E. J.， & Kerlinger， F. N.（1973）. Multiple regression in behavioral research： explanation and prediction. New York： Holt， Rinehart and Winston.

Pierce， C. A.， Block， R. A.， & Aguinis， H.（2004）. Cautionary Note on Reporting Eta-Squared Values from Multifactor ANOVA Designs. Educational & Psychological Measurement， 64（6）， 916-924.

Publications， A. P. A.， on Journal， C. B. W. G.， & Standards， A. R.（2008）. Reporting standards for research in psychology： Why do we need them？ What might they be？ The American Psychologist， 63（9）， 839-851.

R Core Team.（2018）. R： A language and environment for statistical computing. R foundation for statistical computing. Vienna， Austria. Retrieved from https：//www.R-project. org/.

Rouder， J. N.， Morey， R. D.， Verhagen， J.， Province， J. M.， & Wagenmakers， E. J.（2016）. Is there a free lunch in inference？Topics in Cognitive Science， 8（3）， 520-547.

Ryan， R. S.， Wilde， M.， & Crist， S.（2013）. Compared to a small， supervised lab experiment， a large， unsupervised web-based experiment on a previously unknown effect has benefits that outweigh its potential costs. Computers in Human Behavior， 29（4）， 1295-1301.

Smithson， M. J.（2003）. Confidence Intervals. Thousand Oaks， CA： Sage.

Smithson， M. J.（2001）. Correct Confidence Intervals for Various Regression Effect Sizes and Parameters： The Importance of Noncentral Distributions in Computing Intervals. Educational & Psychological Measurement， 61（4）， 605-632.

Steiger， J. H.（2004）. Beyond the F test： Effect size confidence intervals and tests of close fit in the analysis of variance and contrast analysis. Psychological Methods， 9（2）， 164-182.

Steiger， J. H.， & Fouladi， R. T.（1997）. Noncentrality interval estimation and the evaluation of statistical models. In L. L. Harlow， S. A. Mulaik， & J. H. Steiger（Eds.）， What if there were no significance tests？（pp. 221-257）. Mahwah， NJ， USA： Lawrence Erlbaum Assoc Inc.

Wagenmakers， E. J.， Beek， T. F.， Rotteveel， M.， Gierholz， A.， Matzke， D.， Steingroever， H.， ... Gronau， Q. F.（2015）. Turning the hands of time again： a purely confirmatory replication study and a Bayesian analysis. Frontiers in Psychology， 6：494.

Wagenmakers， E. J.， Marsman， M.， Jamil， T.， Ly， A.， Verhagen， J.， Love， J.， ...Morey， R. D.（2018）. Bayesian inference for psychology. Part I： Theoretical advantages and practical ramifications. Psychonomic Bulletin & Review， 25（1）， 35-57.

Wagenmakers， E. J.， Wetzels， R.， Borsboom， D.， & van der Maas， H. L. J.（2011）. Why psychologists must change the way they analyze their data： the case of psi： comment on Bem（2011）. Journal of Personality and Social Psychology， 100（3）， 426-432.