實驗數據的隨機化檢驗及R語言實現

呂小康 付英濤

摘?要?隨機化檢驗是基于實驗中對實驗處理的隨機化分配，通過計算所有可能分配方法的結果得出某一統計量的隨機化分布，并據此進行實驗效應是否存在的統計推斷。相較基于從某一總體中進行重復隨機抽樣而得到抽樣分布推論模式，隨機化檢驗不需要正態總體假定，尤其適合樣本數據存在明顯離群值或小樣本情形，更適合作為隨機化實驗的推論框架。借助免費開源的R軟件及相關軟件包已能快速實現雙處理組和多處理組均值差比較及其他統計量比較的隨機化檢驗，但在心理統計教育與應用中還需進一步推廣。

關鍵詞?隨機化分布; 隨機化檢驗; 顯著性檢驗; 置換檢驗; 心理統計

分類號?B841.2

DOI： 10.16842/j.cnki.issn2095-5588.2019.05.001

1?統計推論中的總體模型與隨機化模型

目前心理統計教材中介紹的統計推論方法大多基于抽樣分布（sampling distribution）的框架，即將樣本數據視為從特定總體中隨機抽樣得到的一次觀測結果，并考慮對該總體進行同樣本容量的重復抽樣，以得到所關注的樣本統計量的假想分布，進而計算相關p值來判斷實驗效應是否存在。心理統計的相關教材、包括其他領域的諸多入門統計教材一般都只是將隨機化實驗得到的數據默認為隨機樣本處理，對數據的正態性進行檢驗后，直接應用抽樣分布進行統計推論。但從嚴格意義上說，這些隨機化實驗的數據并不是在總體中抽樣得到的隨機樣本，并未直接滿足應用抽樣分布進行統計推論的條件。同時，隨機化實驗的目的通常也不是像基于隨機抽樣的研究那樣要求將樣本結論推論至總體、即追求外在效度，而是驗證實驗的處理效應是否真實存在、即追求內在效度。

事實上，統計學中進行統計推論有兩種模型（Ludbrook， 2005）：總體模型（population model）和隨機化模型（randomization model）。將隨機化實驗的數據視為隨機樣本屬于總體模型的思想，此模型假定實驗數據是相應總體的隨機樣本，統計推論用到的抽樣分布常為正態分布或由正態分布推導出的其他理論分布，對正態性假定的依賴性較強。而隨機化模型不需要總體和樣本的假定，其思想基于實驗中的隨機化操作，其統計推論無需依賴正態性前提、而是一種精確分布——隨機化分布（randomization distribution），基于此種分布進行的顯著性檢驗可稱為隨機化檢驗（randomization test）。

基于隨機化分布進行顯著性檢驗的思想，從其起源上講并不晚于基于抽樣分布的顯著性檢驗，但囿于計算便利性上的欠缺而一直沒有得到足夠重視。隨著計算機軟件的發展，隨機化分布的計算或模擬已不是問題，因此其思想又重新得到重視與實踐。隨機化檢驗早期常用來檢驗t檢驗或F檢驗的正確性，Fisher（1936）曾指出與隨機化方法不一致的結論（t檢驗和F檢驗）是不合理的，因為其他方法通常涉及理論上的近似，而數據的真實形態可能并不能夠滿足使用這些近似公式所需要的前提條件。而在當代，隨機化檢驗甚至被一些統計學家認為是“隨機化實驗情形下的金標準”（Edgington & Onghega， 2007），基于隨機化分布的檢驗模式及相關探討日漸增多（Basu， 2011; Dugard， 2014; Lu， Ding， & Dasgupta， 2015; Mielke， Berry， & Johnston， 2011），相關教材也不斷面世（Berry， Johnston， & Mielke， 2014; Berry， Mielke， & Johnston， 2016; Dugard， File， & Todman， 2011）。但此種推論方式目前在國內外心理統計教材中仍介紹不多、在實踐研究中的應用也較少，因此有必要加以說明與推廣。本文將介紹隨機化分布的理論假定及其實現方法，用免費開源軟件R模擬隨機化實驗數據及其隨機化分布，對比隨機化分布和抽樣分布的異同，并提出相應的教學與應用建議。鑒于國內心理學界的教學與研究目前多數仍使用商業化的SPSS或SAS等軟件，對R軟件的認識與應用尚未普及，正文中有少數R語言命令的示范，所有圖片也使用R軟件繪制，以增進國內對該軟件的了解。

2?隨機化檢驗的基本思想

隨機化檢驗的思想其實在20世紀初期就已經出現。較早的一個例子可見于統計學家Fisher（1935）的“女士品茶”名例。其情境大致如下。一名女士聲稱自己可以辨別奶茶里面先放的奶還是先放的茶，Fisher想通過實驗驗證這一點。故選取8杯奶茶，隨機選取其中4杯先放奶，另外4杯先放茶，其他條件保持一致。以隨機順序讓女士品嘗后辨別出哪4杯先放了奶，哪4杯先放了茶。結果如表1。

該女士正確辨別出了先加奶的4杯中的3杯，能否據此說明該女士具有辨別能力？Fisher的推論模式如下：假設該女士沒有辨別能力，那么其判斷是完全隨機的，此時的辨別結果共有84=70種。其中（從判斷先加奶的4杯來說），0對4錯有1種;1對3錯有16種;2對2錯有36種;3對1錯有16種;4對0錯有1種。則得出此結果的概率為p=17/70=0.24。從雙側檢驗的角度看，此結果的p=34/70=0.486。故以0.05的顯著性水平看，不能由此認為該女士具有辨別能力;在這個實驗設計中，此顯著性水平下只有該女士全部辨別正確，才可以認為她具有辨別能力。

此例中隨機化檢驗的思想已有所體現，即在原假設成立的條件下，根據所有可能的實驗結果判斷出現實際結果的可能性。但嚴格來說，Fisher的這種檢驗思想應稱為置換檢驗（permutation test，其中permutation即排列的意思）而不是隨機化檢驗，因為這一實驗中并未涉及隨機化分組。隨機化檢驗實際上利用了置換檢驗的計算方式進行p值計算，但置換檢驗本身不一定僅適用于隨機化實驗的情形，也可適用于隨機抽樣的情形，是含義更為寬泛的一種檢驗。換言之，隨機化檢驗可視為置換檢驗的一個子集（Edgington & Patrick， 2007）。不過，由于兩者的區分主要在應用情境的區別而非計算方法的區分，在實際使用中兩種方法也常被視為是同一種方法。

此外，Fisher（1935）在另一個配對比較問題中應用了隨機化檢驗的思想。問題是比較有15個觀測值的配對樣本，兩個樣本的差異值是314。在此配對設計中給被試隨機分配實驗處理共有215種方式，在零假設條件下，所有可能的結果中有1726種情況大于等于314，即p=0.05267。而根據抽樣分布得出的t值算出的p=0.0497，兩者相差較小。

在Fisher（1925）、Geary（1927）、Eden和Yates（1933）、Pitman（1937a， 1937b， 1938）等人置換檢驗思想的基礎上，Kempthorne（1955）等人開始著手發展更具一般性的隨機化分布及檢驗的理論框架。實驗設計中比較重要的一步是給被試分配實驗處理，隨機化要求這一過程在實驗的約束條件下（比如區組內）是完全隨機的，即在有限的所有可能的分配方式中隨機選取一種，每種方式被選中的概率相等。選定一個統計量，計算零假設條件下所有可能的分配方式下該統計量的值，即得到該統計量的隨機化分布。根據實驗結果得出的統計量在隨機化分布中的相對位置和設定的顯著性水平，即可得出相應p值并判斷是否拒絕零假設。

Kempthorne（1955）提出，隨機化分布的應用依賴于被試—處理可加性假定（unit-treatment additivity）。其基本思想如下：每名被試的觀測值可以視為被試本身的基本量和所接受處理效應的加和。用i表示參加實驗的被試，i=1，2 …，N;t表示實驗處理，t=1，2，…，T。隨機分配每名被試接受一種實驗處理，如果被試i接受了實驗處理t，得到的觀測值可以表示為：

在假設實驗處理效應相同的條件下，只需要對實驗結果進行隨機化排列即可得到所有可能的結果，進而選擇某個適合的統計量并計算它在每種分配方式下的取值，就可以得到該統計量對應的隨機化分布。再通過計算該分布中如此次樣本觀測值這么極端、更為極端值（所謂“極端”即指偏離原假設的設定）占整個分布中所有可能取值的比例，即可得到相應p值。這就是利用隨機化分布進行顯著性檢驗的基本模式。

隨機化分布的思想框架較為直觀，并不需要假想存在實驗處理組之外的一個“（正態）總體”，這對于實際研究者理解統計推論的思維框架是較為便利的。問題在于其計算過程比較麻煩。隨著樣本量和處理組數的增加，實驗結果的可能性會大大增加;對于復雜問題的可能結果排列需要花費相當長的時間，往往超過手動計算或公式推導的可能。因此隨機化檢驗在計算機軟件興起之前并未得到太多重視。但隨著計算機的發展，隨機化結果的計算不再是問題，并且可以通過軟件對隨機化分布實現可視化，理論假定更少、結果更加精確的隨機化檢驗又逐漸開始受到重視（Ludbrook & Dudley， 1998; Rubin， 1991）。

3?基于隨機化分布的統計推論示例：基于R的應用

隨機化檢驗通常用于檢驗不同實驗組之間的處理效應是否真實存在，故通常不能應用于單樣本數據的情形。這里僅就最一般意義上的雙處理組和多處理組情形做出示例。

3.1?雙處理組情形：與傳統t檢驗的比較

不妨先考慮隨機分配被試到兩種實驗處理的情況，此時的隨機化過程發生在被試之間，實驗結果為獨立的雙樣本數據。用R模擬服從特定正態分布的隨機數，樣本量為7。

此時=20.29，s2x=18.90，=15.57，s2y=21.95。能否根據上面的數據得出結論：實驗處理X的效果大于處理Y的效果？

這顯然是一個單側檢驗問題。基于傳統抽樣分布的統計推斷模式如下：將兩種實驗處理下的結果看作是來自兩個獨立同方差的正態分布總體的簡單隨機樣本。結果可算得t=1.95，p=0.037，在0.05顯著性水平下可認為實驗處理X的效應大于Y。由于這一檢驗公式較為常見，故這里不再具體敘述相關過程。R中的命令如下：

t.test（X， Y， var.equal=TRUE， alternative="greater"） # 執行同方差前提下的雙樣本單側t檢驗

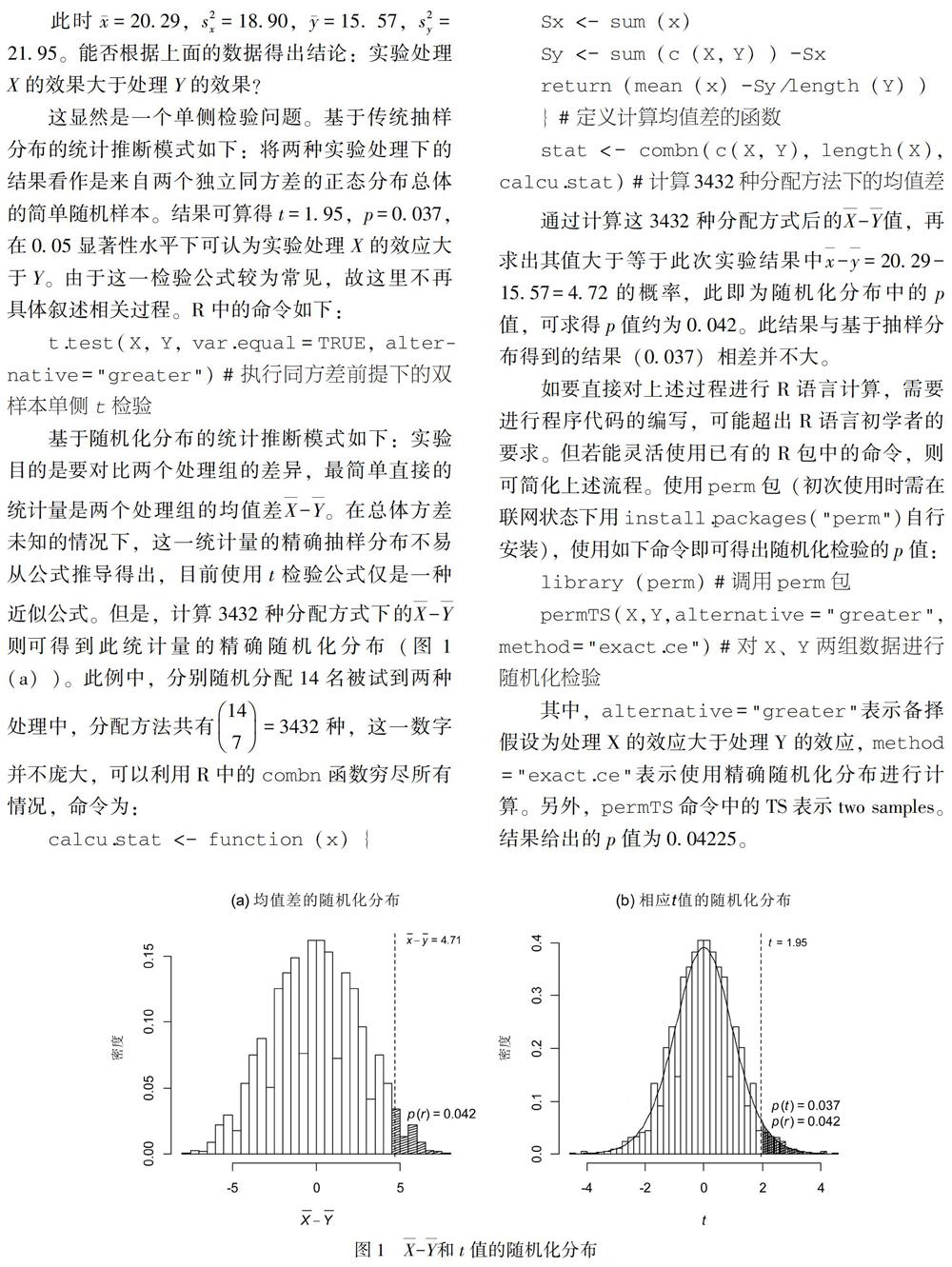
基于隨機化分布的統計推斷模式如下：實驗目的是要對比兩個處理組的差異，最簡單直接的統計量是兩個處理組的均值差X-Y。在總體方差未知的情況下，這一統計量的精確抽樣分布不易從公式推導得出，目前使用t檢驗公式僅是一種近似公式。但是，計算3432種分配方式下的X-Y則可得到此統計量的精確隨機化分布（圖1（a））。此例中，分別隨機分配14名被試到兩種處理中，分配方法共有147=3432種，這一數字并不龐大，可以利用R中的combn函數窮盡所有情況，命令為：

calcu.stat<-function（x）{

Sx<-sum（x）

Sy<-sum（c（X， Y））-Sx

return（mean（x）-Sy/length（Y））

} # 定義計算均值差的函數

stat<-combn（c（X， Y）， length（X）， calcu.stat） # 計算3432種分配方法下的均值差

通過計算這3432種分配方式后的X-Y值，再求出其值大于等于此次實驗結果中x-y=20.29-15.57=4.72的概率，此即為隨機化分布中的p值，可求得p值約為0.042。此結果與基于抽樣分布得到的結果（0.037）相差并不大。

如要直接對上述過程進行R語言計算，需要進行程序代碼的編寫，可能超出R語言初學者的要求。但若能靈活使用已有的R包中的命令，則可簡化上述流程。使用perm包（初次使用時需在聯網狀態下用install.packages（"perm"）自行安裝），使用如下命令即可得出隨機化檢驗的p值：

library（perm） # 調用perm包

permTS（X，Y，alternative="greater"， method="exact.ce"） # 對X、Y兩組數據進行隨機化檢驗

其中，alternative="greater"表示備擇假設為處理X的效應大于處理Y的效應， method="exact.ce"表示使用精確隨機化分布進行計算。另外，permTS命令中的TS表示two samples。結果給出的p值為0.04225。

除此之外，還可以另一種思路進行隨機化檢驗，即計算每種排列情形下的傳統雙樣本t檢驗觀測值，從而求出此t值的隨機化分布。再基于分布計算此次實驗中的t觀測值在多大程度上偏離原假設（t=0），從而得到相應p值。圖1（b）是覆蓋了t分布曲線的隨機化分布，p（r）表示隨機化（randomization）情形下的p值，p（t）表示傳統抽樣分布t檢驗下的p值。此次實驗得出的結果為t=1.95，在此隨機化分布中p（t≥1.95）=0.042。顯然，以X-Y作為統計量計算出的p值和以t值作為統計量得出的p值相同，這是因為根據每種分配方式的結果計算出的t值和X-Y是一一對應的。

對于上述實驗處理數和樣本量比較少的情況，可以計算所選統計量的精確隨機化分布，這里所謂“精確”（exact），其實只是“完整”的意思，即窮盡了所有可能的隨機分配情況。但在實際研究中經常會遇到實驗處理和樣本量比較多的情況，即使有計算機的幫助，計算所有的分配方式也往往不現實，但可以在R中運用sample函數進行一定次數的模擬，即在所有可能的分配方式中進行重復抽樣，得出近似隨機化分布。用R對此例進行10000次抽樣得出的近似隨機化分布，p值為0.039，與精確隨機化分布稍有差異，這是因為隨機取樣所產生的抽樣誤差所致。

現考慮上文中的隨機數為配對樣本的情形。傳統t檢驗模式下，可算得p值為0.08248，在0.05的顯著性水平下沒有充分理由認為 X的實驗處理效應顯著高于 Y 的實驗處理效應。R語言命令如下：

t.test（X， Y， paired=TRUE， alternative="greater"）

如果采用隨機化檢驗，此例中由于隨機化發生在每個被試內部，每個被試共有2種處理分配順序，故共有27=124種分配方式。通過計算每種分配方式下的配對均值差，即可得到其精確隨機化分布。再計算此分布中大于等于此次實驗結果中的配對差值所占的比例，即可得到相應p值。這里使用exactRankTests包中的函數來做示范。

library（exactRankTests）

perm.test（X， Y， alternative="greater"， paired=TRUE）

結果給出的p值為0.09375，與配對樣本t檢驗的結果也很接近。

3.2?多處理組情形：與傳統方差分析的比較

如果把上例中實驗處理數擴大為四組，其結果如表3。其中A、B、C和D的數據分別取自正態分布總體N1（20， 52），N2（17， 52），N3（15， 52），N4（13， 52）。其命令如下：

檢驗多個實驗組的均值是否具有顯著差異的常用方法是方差分析。此例中所有樣本數據來自同方差的正態總體，故適宜使用傳統方差分析進行顯著性檢驗，結果為F=3.74，p=0.0246，在0.05顯著性水平下可認為各實驗處理的效應并不完全相同。對應的R語言命令如下（這里先對數據格式進行變動，以變成軟件處理所需要的長格式數據）：

dataABCD<-data.frame（A， B， C， D）

library（tidyr） # 調用tidyr包，以進行數據操縱

ABCD<-gather（dataABCD， group， value， factor_key=TRUE） # 將數據變成長格式數據，各分組信息存為一列，命令為group，各取值信息存為另一列，命令為value，factor_key=TRUE 用于確保group為因子變量、即類型變量

fit1<-aov（value～group， data=ABCD） # 進行方差分析

summary（fit1） # 給出方差分析結果

基于隨機化分布的統計推斷模式如下。此例中隨機分配28名被試到4種處理中的方式共有

287×217×147×77=4.73×1014

種。此時要窮盡所有的分配方式得出精確的隨機化分布是不現實的，但可以通過對所有分配方式的隨機抽樣得到近似的隨機化分布。先選取F值作為統計量，分別計算每種分配方式下的F統計量即得其近似隨機化分布，再根據此分布、此次觀察結果得到的F值，即可算出相應p值。F值得隨機化分布如圖2，由此得到的p值為0.0226，這與傳統F檢驗的結果非常接近。

c=10000 # 設定模擬次數

F.stat<-numeric（c） # 構建F統計量變量

F.stat[1]<-summary（aov（value～group， data=ABCD））[[1]][4][[1]][1] # 設此次觀察為第一個值

set.seed（1234） # 設定循環種子數

for（i in 2：c）{

F.stat[i]<-summary（aov（sample（value）～group， data=ABCD）） [[1]] [4][[1]][1]

} # 隨機抽取其他分配方法的F值

p=mean（F.stat>=F.stat[1]） # 計算p值

對上述過程進行編程計算稍顯麻煩，使用用coin包中的函數可簡介上述過程：

library（coin）

oneway_test（value～group， data=ABCD， distribution=approximate（B=10000））

其中B=10000即表示進行10000次模擬。計算結果可得p值為0.02433。這與傳統F檢驗的p值非常接近。實際上，當方差分析的假定未被明顯違背時，隨機化檢驗的優勢并不明顯。但當數據明顯呈現偏態、尤其是各組方差相差較大時，使用傳統檢驗方法會存在統計上二類錯誤的增大問題，此時使用隨機化檢驗來做判定則可使統計決策更為穩健。值得注意的是oneway_test函數使用的隨機化檢驗方法為Pitman-Fisher法，其檢驗統計量的選取與前面的模擬有所不同，具體可參見Boik（1987）。

下面考慮隨機區組設計的情形。將表2問題的表述稍作變動，假設表中的數據是7個區組接受4種實驗處理的情況，每個區組有4名被試，每名被試隨機接受一種實驗處理。此時就變成了一個隨機區組問題，從數據處理方法上講則是雙因素方差分析的過程。傳統方差分析結果為F=3.46，p=0.0382。R中的命令如下：

library（dplyr）

block<-as.factor（c（1：7）） # 生成區組標簽

blockABCD<-data.frame（A， B， C， D， block）

newABCD<-gather（blockABCD， group， value，-block， factor_key=TRUE）

fit2<-aov（value～block+group， data=newABCD）

summary（fit2）

隨機化檢驗的模式如下。在4種處理沒有差異的原假設下，由于對隨機化在區組內進行，此時隨機化分配方式共有（4×3×2×1）7=4586471424種。雖然用軟件可以一一計算各分配下的F值，但耗時較長，故仍可考慮使用隨機抽樣的方式進行模擬。這里只用coin包中的oneway_test函數進行示范。

library（coin）

oneway_test（value～group | block， data=newABCD， distribution=approximate（B=100000）） # | block表示指定區組名稱

結果得到的p值為0.03259，與傳統檢驗的結果也很接近。

4?隨機化分布和抽樣分布的比較：樣本量與離群值的影響

對于正態性擬合良好的數據，抽樣分布是隨機化分布的良好近似。在圖1（a）和圖2中，將t分布和F分布曲線覆蓋在相應隨機化分布上，兩者均擬合良好。這是因為用R模擬的數據均是來自正態分布總體，數據的正態性可以得到保證。下面以兩個處理組的情況為例，考慮兩個影響數據正態性的因素——樣本量和離群值（outliers）。

此處考慮服從偏態分布和正態分布的兩種數據。對數正態分布是一種右偏態分布，對服從對數正態分布的數據取對數可以得到正態分布數據。圖3（a），（c），（e）的樣本是從對數正態分布中抽樣得到的右偏態數據，樣本量分別為5，10和20。圖3（b），（d），（f）的樣本是對相應樣本量的右偏態數據取對數得到的正態數據。

取樣本量為5的偏態樣本程序如下：

set.seed（123）

x<-rlnorm（5， 1）

set.seed（321）

y<-rlnorm（5， 0.5）

其他樣本量的情形可依此得出。圖3中可以直觀地看到不同分布形態和不同樣本量的數據對隨機化分布和t分布擬合狀況的影響。可以發現：（1）偏態數據和正態數據相比而言，正態數據的隨機化分布和t分布擬合得較好，這一點在樣本量較小的情況下體現得尤其明顯;（2）當樣本量較小的時候，即便對于正態性數據而言，抽樣分布與隨機化分布的擬合狀況也是比較差的;（3）而樣本量較大時，即使數據呈現偏態，抽樣分布與隨機化分布也擬合得較好，這正是傳統t檢驗在雙處理組數據中得到普遍應用的原因之一。

另外，比較由隨機化分布和t分布得出的p值可以作為衡量擬合狀況的一個指標。圖4是對于偏態數據而言，樣本量從5～50變化時，由隨機化分布和t分布得出的p值變化。圖4（a）隨機化分布p值和t分布p值隨樣本量的變化情況，（b）是兩個p值差隨樣本量的變化情況。

從圖4可以看出，總體而言隨機化分布和t分布得出的p值是比較一致的。對于偏態數據而言，樣本量的增加可以有效地使p值減小，尤其是在樣本量增加到30之后。這一方面增大了統計檢驗力，另一方面也使隨機化分布和t分布得出的p值差異逐漸減小。

下面考慮離群值的影響。以表2中的數據為例，圖5中（a），（b），（c），（d）是假設表2中X組最大值分別為28，38，48，58時的隨機化分布。可以發現，離群值距離均值越遠，隨機化分布和t分布的擬合狀況越差，根據兩者得出的p值相差越大。Ernst（2009）通過設置樣本最小值的方法探討了離群值對隨機化分布和t分布擬合狀況的影響，與此結論一致。由于t檢驗假定其數據是取自正態分布總體的隨機樣本，因此當不能保證樣本的隨機性和正態性時，t檢驗的結果理論上不能保證其準確性。而基于隨機化分布的檢驗不需要正態性假定，也無需隨機樣本。若其分布呈現偏態、樣本量較少或存在離群值時，基于隨機化分布的檢驗結果更令人信服。不過，當樣本量較大時，t檢驗的結果對數據的正態性要求不高，與隨機化分布的結果差異不大。

5?總結與建議

隨機化檢驗依賴于實驗處理的隨機化分配和處理效應的可加性假定，不適合觀測數據，但較適合具有兩個或多個處理組的隨機化實驗結果的顯著性檢驗。在推理框架上，隨機化檢驗并不需要假想總體的存在，這更有利于初學者理解隨機化實驗的實際情境，更適宜作為隨機化實驗的統計推論框架。同時，隨機化檢驗并不需要假定總體的分布形態，因此比基于抽樣分布的假設更具靈活性，可以適用于傳統顯著性檢驗不能勝任的情形。雖然目前隨機化實驗的顯著性檢驗常常通過抽樣分布理論給出，這是因為很多情況下抽樣分布理論對數據正態性的要求并不十分嚴格。隨著實驗處理數和被試數的增多，基于抽樣分布的顯著性檢驗與基于隨機化分布的顯著性檢驗越來越接近。在許多情況下，兩者在實驗處理數和被試數較少時仍有良好的近似性。因此，運用抽樣分布對隨機化實驗的結果進行推論多數情況下是比較可靠的。

但在以下幾種情況中，建議基于隨機化分布進行推論而非抽樣分布，或者至少將隨機化分布的結果作為必要參考。（1）樣本數據量過少。樣本數據量過少帶來的問題是無法保證數據的正態性，即使是從正態總體中抽取的小樣本，抽樣分布和隨機化分布的擬合狀況也很差。（2）樣本中存在較嚴重的離群值。此時或者找出產生離群值的原因，將離群值進行剔除使數據符合抽樣分布條件，或者沒有合理的理由剔除離群值，此時需考慮隨機化分布方法。（3）需選取的統計量難以從公式推導得出。隨機化分布的統計量選取更加自由，許多統計量的抽樣分布難以計算，但是研究者可以根據需要選擇合適的統計量計算其隨機化分布。例如離群值對于抽樣分布的統計量往往影響較大，但對中位數、四分位數之類的統計量影響就較小，它們的理論分布通常難以求得。除此之外，對于計數數據和等級數據而言，常常利用一些近似估計和檢驗，可能會造成近似誤差，此時隨機化分布的應用更應當得到重視（Eudey， Kerr， & Trumbo， 2010）。

最后需要說明的是，對于心理統計的教育與應用而言，隨機化檢驗的思想并不復雜，但計算比較繁瑣，教學過程中可以借助R之類的軟件進行輔助教學或計算。這需要對軟件的應用有一定了解。鑒于目前R、Python等開源統計軟件尚未成為國內心理統計主流軟件，加強對此類軟件的宣傳和應用仍是必要的。實際上，這些軟件已經具備不亞于SPSS或SAS的統計分析功能，在某些方面甚至更勝一籌。促進軟件應用的開源化、免費化，對于國內的心理學教學和研究單位節省統計軟件方面的支出或避免軟件使用上的版權問題，也是具有積極意義的。其中，除了文中提到的perm、exactRankTests、coin等R包外，還有ez、AUtests、flip、jmuOutlier、jmuOutlier、treeperm等軟件包提供了豐富的隨機化檢驗函數與算法，可供研究者進一步探索利用。當然，相較于發展更為成熟的總體模型推論，一些復雜實驗設計的隨機化檢驗模式仍還有待開發，基于這一模式的統計功效與效應值探討也還有待深入。

參考文獻

Basu， D.（2011）. Randomization analysis of experimental data： The fisher randomization test. Journal of the American Statistical Association， 75（371）， 305-325.

Berry， K. J.， Johnston， J. E.， & Mielke， Jr， P. W.（2014）. A chronicle of permutation statistical methods： 1920-2000 and beyond. Cham， Switzerland： Springer.

Berry， K. J.， Mielke， Jr， P. W. & Johnston， J. E.（2016）. Permutation statistical methods： an integrated approach. Cham， Switzerland： Springer.

Boik， R. J.（1987）. The fisher-pitman permutation test： A non-robust alternative to the normal theoryFtest when variances are heterogeneous. British Journal of Mathematical & Statistical Psychology， 40（1）， 26-42.

Box， G. E. P.， & Anderson， S. L.（1955）. Permutation theory in the derivation of robust criteria and the study of departures from assumption. Journal of the Royal Statistical Society， 17（1）， 1-34.

Dugard， P.（2014）. Randomization tests： A new gold standard？Journal of Contextual Behavioral Science， 3（1）， 65-68.

Dugard， P.， File， P.， & Todman， J.（2011）. Single-case and small-n experimental designs： A practical guide to randomization tests. London： Routledge.

Eden， T.， & Yates， F.（1933）. On the validity of Fishersztest when applied to an actual example of non-normal data. Journal of Agricultural Science， 23（1）， 6-17.

Edgington， E. S.， & Onghena， P.（2007）. Randomization tests. Boca Raton， FL： CRC Press.

Ernst， M. D.（2009）. Teaching inference for randomized experiments. Journal of Statistics Education， 7（1）.

Eudey， T. L.， Kerr， J. D.， & Trumbo， B. E.（2010）. Using R to simulate permutation distributions for some elementary experimental designs. Journal of Statistics Education， 18（1）.

Fisher， R. A.（1925）. Statistical Methods for Research Workers. Edinburgh： Oliver and Boyd.

Fisher， R. A.（1935）. The Design of Experiments. Edinburgh： Oliver and Boyd.

Fisher， R. A.（1936）. The coefficient of racial likeness and the future of craniometry. The Journal of the Royal Anthropological Institute of Great Britain and Ireland， 66， 57-63.

Geary， R. C.（1927）. Some properties of correlation and regression in a limited universe. Metron Rivista Internazionale de Statistica， 7， 83-119.

Kempthorne， O.（1955）. The Randomization Theory of Experimental Inference. Journal of the American Statistical Association. 50（271）， 946-967.

Lu， J.， Ding， P.， & Dasgupta， T.（2015）. Construction of alternative hypotheses for evaluation of randomization tests with ordinal outcomes. Statistics & Probability Letters， 107（12）， 348-355.

Ludbrook， J. & Dudley， H. A. F.（1998）. Why permutation tests are superior tot- andF-tests in biomedical research. The American Statistician， 52（2）， 127-132.

Ludbrook， J.（2005）. Randomization based tests. Encyclopedia of statistics in behavioral science. Hoboken， NJ： John Wiley & Sons， Inc.

Mielke， P. W.， Berry， K. J.， & Johnston， J. E.（2011）. Robustness without rank order statistics. Journal of Applied Statistics， 38（1）， 207-214.

Pitman， E. J. G.（1937a）. Significance tests which may be applied to samples from any populations. Supplement to the Journal of the Royal Statistical Society， 4（1）， 119-130.

Pitman， E. J. G.（1937b）. Significance tests which may be applied to samples from any populations II： The correlation coefficient test. Supplement to the Journal of the Royal Statistical Society， 4（2）， 225-232.

Pitman， E. J. G.（1938）. Significance tests which may be applied to samples from any populations III： The analysis of variance test. Biometrika， 29（201）， 322-335.

Rubin， D. B.（1991）. Practical applications of modes of statistical inference for causal effects and the critical role of the assignment mechanism. Biometrics， 47（4）， 1213-1234.