統計檢驗力的分析流程與多層模型示例

趙禮 王暉

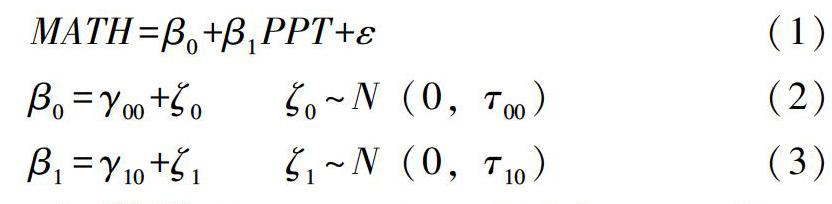
摘?要?影響統計檢驗力的因素包括研究設計因素、研究工具因素和統計學因素。統計檢驗力分析是實驗設計中非常重要的一部分：先驗統計檢驗力分析可以幫助研究者在實驗開始之前確定樣本量以節約人力物力;后驗統計檢驗力分析可以在研究完成之后幫助研究者審視研究效力，為后續研究提供幫助。當研究問題或實驗設計較為復雜時，可借助Optimal Design設計多階層統計檢驗力分析。建議在本科及研究生階段重視統計檢驗力分析的教學，在科研中注重統計檢驗力分析的應用，以優化實驗設計并增加研究結果的可靠性。

關鍵詞?統計檢驗力; 多層分析; 效應量; 假設檢驗; Optimal Design

分類號?B841.2

DOI： 10.16842/j.cnki.issn2095-5588.2019.05.002

統計檢驗力（power）是指能正確拒絕錯誤的零假設（null hypothesis）的概率，是經典統計決策理論和假設檢驗模式中不可缺少的一部分。近年來，統計檢驗力分析越來越受到重視，很多學術期刊已經明確要求研究者在論文中提供統計檢驗力相關內容。但在目前國內的心理學教學與研究過程中，統計檢驗力分析仍未得到充分的重視。本文著重探討了統計檢驗力影響因素和基本分析流程，并且討論了統計檢驗力分析中可能遇到的實際問題，并借助Optimal Design來展示如何設計多階層統計檢驗力分析，可為當下心理學教學與研究中統計檢驗力分析與應用提供參考。

1?統計檢驗力的影響因素

影響統計檢驗力的因素有很多，主要包括研究設計因素、研究工具因素和統計學因素。

第一，研究設計因素。例如，問卷設計中存在的雷區不只會對研究數據產生影響，也會影響統計檢驗力。在用詞與表述上，研究者不應使用復雜難懂、過于專業的詞匯。研究問題不應對被試造成引導性影響，諸如“你是否同意流產——一種謀殺無辜人類的做法——應該取締？”這樣的問題在研究中應當避免。除有意引導外，一些問題可能會因其表意含糊不清而產生歧義。另外，非開放式問題通常比開放式問題的檢驗力要高，因為開放式問題的答案多樣性更高。這些用詞與表述問題會使得研究隨機誤差增加，從而降低統計檢驗力。并且，由于取悅效應以及研究中可能涉及敏感問題的存在，被試可能會隱藏他們的真實想法，從而導致組間差異變小，進而降低檢驗力，因此實驗中的保密和匿名原則很重要。同樣，實驗的設計也會影響統計檢驗力。如果被試間的差異可以得到控制，統計檢驗力會增加，例如重復測量設計比獨立樣本設計的統計檢驗力要高。但是不可單純追求控制被試差異，在取樣過程中，如果抽樣框架是錯誤的（例如包括非理想群體或者理想群體被排除），檢驗力也會降低。

第二，研究工具因素。例如，量表的精細程度會影響統計檢驗力。粗糙的量表會造成相關系數的降低（Aguinis， Pierce， & Culpepper， 2009），這類問題是由于研究工具本身所決定的。例如，李克特量表可以用來測量被試的態度（例如1表示非常不同意，5表示非常同意），然而由于量表本身的限制，被試只能在1到5這五個數字中選擇，從而造成1.6與2.6或者2.7與3.4之間的比較無法測得，進而降低統計檢驗力。

第三，統計學因素。（1）數據的范圍限制會影響統計檢驗力。例如，要研究大學GPA和課堂出勤率的關系，如果對GPA的范圍加以限制，例如只選取GPA在1～4之間的學生，從而導致研究相關關系的數據受限，會造成統計檢驗力降低。（2）違反統計假設也會造成統計檢驗力的降低（Maxwell， Delaney， & Kelley， 2018）。例如對于統計檢驗力的分析通常基于正態分布的假設，如果違反此假設則需要對統計檢驗力重新進行解釋。非參數檢驗（例如Kruskal-Wallis H檢驗）可以應用在非正態分布的情況，并且變量的轉換（例如對數轉換）可以改變分布的形狀使其為正態分布。（3）測量的信度也會影響統計檢驗力，通常長測驗比短測驗要更加可靠，因為長測驗的變異性較低（Coe， 2002）。例如一個有100個項目的測驗的標準差比一個有10個項目的測驗標準差要低，所以信度較高，進而統計檢驗力較高。（4）連續變量二分化會降低統計檢驗力（Altman & Royston， 2006），此過程會導致很多信息丟失。假設研究學生身高和體重之間的關系，如果把收集到的數據只分為“高”“矮”兩類，那么身高和體重之間相關關系的測量會因為身高變量的變異性降低而降低準確性。

2?統計檢驗力分析的組成部分

統計檢驗力分析的主要組成部分為：效應量、樣本量、第一類錯誤率（α）和第二類錯誤率（β）。各成分對統計檢驗力的影響在已有文獻中已有不少討論與總結（參見吳艷，溫忠麟，2011;

溫忠麟，范息濤，葉寶娟，陳宇帥，2016;

鄭昊敏，溫忠麟，吳艷，2011），在本文中將不做重復說明與討論，只在說明此四部分間基本關系的基礎上，再做一些補充。

四成分之間的基本關系如下：（1）效應量和樣本量結合可得非中心參數，即零假設樣本分布和備擇假設樣本分布之間的區別。效應量可影響統計檢驗力，兩總體分布的差異可以影響效應量，進而影響統計檢驗力。當差異增大時，統計檢驗力增大，反之亦然。（2）樣本量越大則統計檢驗力越大。（3）隨著第一類錯誤率的增大（例如從0.01到0.05），第二類錯誤率會降低，所以統計檢驗力（1-β）會升高。（4）與使用不同水平的情況類似，使用單側檢驗或者雙側檢驗也對統計檢驗力有影響。在同一自由度下，單側檢驗比雙側檢驗要更加具有統計檢驗力。（5）當變異性增大時，統計檢驗力會變弱。例如由于影響被試間差異的因素得到了控制，重復實驗設計的統計檢驗力更高。

在計算效應量時，觀察值（例如1，2）和變異性（例如s）都假設與其真實的參數值（例如μ1，μ2和σ）相等。然而這些真實的參數值很難測得，所以需要估計效應量的值。Howell（2017）提到三種估計效應量的方法：（1）根據先前的研究來決定效應量。具體來說，先前的研究可以提供樣本均值和標準差的相關信息，這些信息可以用來作為其他研究中假定可以體現實驗處理效應的參數值的參考。（2）在沒有相似的先前研究時，效應量的估計則應建立在個人評估的基礎上，即研究者主觀認為的重要差異的大小（μ1-μ2）。假如研究者想研究一種減肥藥，他們決定此種減肥藥有效的標準為可以使個體減重5 kg，那么減肥前后的差異（5 kg）就可以用來計算效應量。此選定的差異值可以在正式實驗之前通過試驗研究（pilot study）來獲取經驗。例如在社會心理學研究中，研究者經常會研究一些特別新奇的問題，所以他們會在正式研究之前來做試驗研究得到可能有實驗處理效應的差異值。這個方法不僅可以用來估計效應量，也可以幫助研究者找出錯誤，從而避免人力物力的浪費。（3）Cohen指導值（表1）（Cohen， 1988， 1992）。

根據不同的效應量水平，研究者可以計算出在某一顯著性水平下達到某檢驗力的樣本量的范圍。通過10000個研究的元分析發現平均效應量為0.5（Lipsey & Wilson， 1993），一般推薦研究者為達到足夠統計檢驗力的效應量為0.8（Lenth， 2001）。

在以上三種方法中，方法（1）是最為推薦的，當方法（1）和方法（2）都不可用時才根據方法（3）來估計效應量，其原因為此方法中三個水平在一定程度上說為任意制定的（Howell， 2017）。并且Lenth（2001）提出研究者不能只依據計算效應量時的分子和分母的比，也應依據分子和分母本身的數值，因為在先前提到的減肥例子中，研究者不僅應該注重被試服藥前后體重的差和樣本標準差的比，也應注重被試服藥前后體重本身數值的差，更進一步地說，應注重服藥前后體重本身的數值。

3?統計檢驗力分析的兩大類型

3.1?先驗檢驗力分析

統計檢驗力分析是實驗設計中的重要的一部分，此分析可以幫助研究者更加深入地思考如何開展該研究，例如思考如何對實驗設計進行優化。由于假設檢驗在社會和行為科學中的實證研究有著非常廣泛的應用，在實驗研究開始之前研究者通常要對研究做出統計檢驗力分析來確定能夠檢測到統計學差異的必要樣本量（吳艷，溫忠麟，2011）。一些研究人員不重視對研究進行統計檢驗力分析，他們在研究的過程中發放數以百計，甚至數以千計的問卷來收集數據，然而事實上，這些研究不需要如此之大的樣本量，這樣就造成了人力物力的浪費，然而這些浪費只需要進行先驗檢驗力分析（priori power analysis）就可以避免。所以，一個合理的樣本數量在實驗設計中是非常重要的，特別是在經費緊張或者需要人類作為被試的情況下。

3.2?后驗檢驗力分析

后驗檢驗力分析（post-hoc power analysis）是在數據收集和分析之后進行的統計檢驗力分析。當樣本量和效應量（effect size）都已知的情況下，統計檢驗力可以在某個指定的顯著性水平（significance level）（例如0.05，0.01）下計算得到。很多科學家推薦進行事后分析，特別是在研究結果不顯著以及效應量分析為中和大時（吳艷，溫忠麟，2011;Lenth， 2001）。

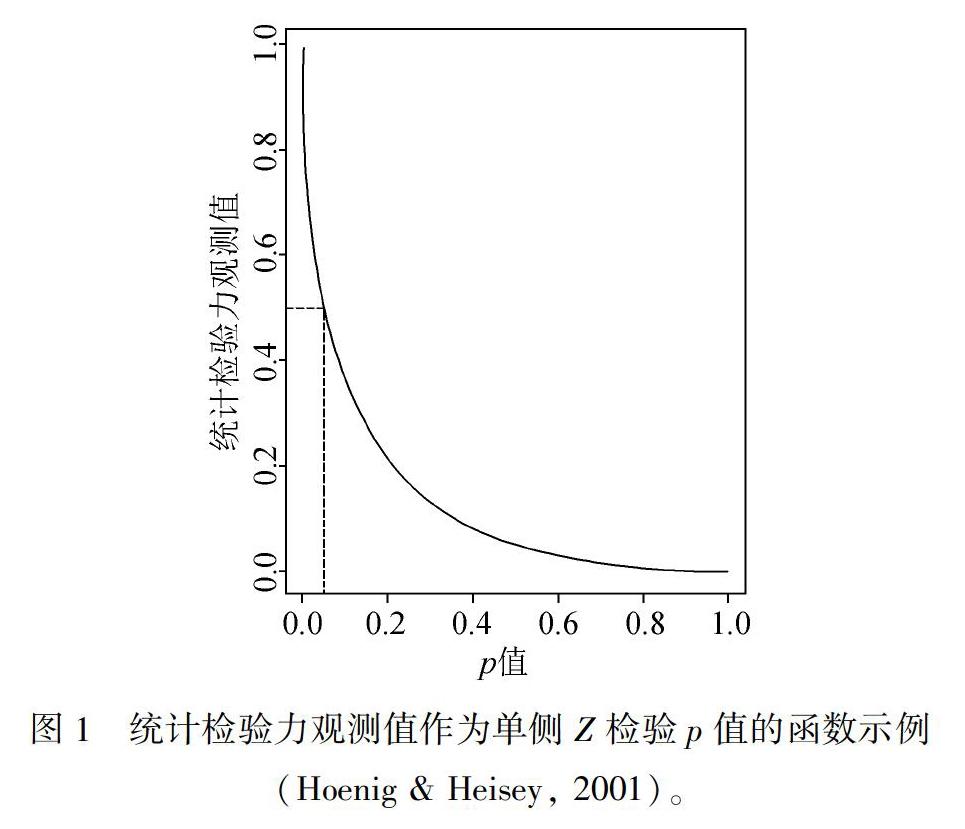
然而，在實際操作中存在不少不恰當使用后驗檢驗力分析的情況。一些研究者認為統計顯著性未達到（例如，p>0.05）且基于效應量觀測值計算得到的統計檢驗力值較高的情況為零假設為真提供了證據，然而這種后驗檢驗力分析是不正確的。Hoenig和Heisey（2001）指出統計檢驗力值是p值的1∶1函數，一旦得知p值，那么計算所得的統計檢驗力值也就不再提供新的信息。并且此1∶1函數使得非顯著p值與低統計檢驗力值相對應（圖1）。當p值為0.05時，相對應的統計檢驗力值為0.5。當p值增大時，統計檢驗力觀測值則會降低，所以拒絕零假設的同時又有高后驗檢驗力值的情況是不可能的。例如，如果統計檢驗力值1 為0.4，統計檢驗力值2 為0.2，基于圖1它們分別對應的p值大約為0.075和0.225。所以越高的統計檢驗力值代表了越大拒絕零假設的幾率，而不是為證明零假設為真提供更多的證據。

后驗檢驗力分析的另一個應用為得出可檢測效應量（detectable effect size），此效應量可根據變異性和預期統計檢驗力（例如0.8）計算而得。此后驗檢驗力分析應用的支持者認為根據此方法得到的效應量為真實效應量的上限，即真實的效應量越是接近可檢測效應量，那么零假設為真的可能性則越大。然而使用后驗檢驗力分析來計算可檢測效應量是不科學的。第一，在同等顯著性水平下，若兩個實驗的結果均不顯著、兩總體均值差和樣本量均相同，且如果（假設為Z檢驗）Z1>Z2，則標準差σ1>σ2。因為可檢測效應量可以通過預期統計檢驗力（例如0.8）和觀測標準差的值（例如σ1，σ2）計算而得，那么第一個實驗的可檢測效應量應小于第二個實驗的相應值，又由于σ1<σ2，那么第一個實驗中的總體均值差要小于第二個實驗的相應值。因為Z1>Z2且具有統計顯著性的兩總體均值差是真實差值的上限，那么真實差值越接近具有統計顯著性的差值，則拒絕零假設的可能性越大。第二，如果兩實驗在同等統計顯著性水平和樣本量下都有非顯著的實驗結果，且Z1>Z2，那么估計效應量應為：效應量1>效應量2，假設兩實驗的標準差相等，那么要想達到理想的統計檢驗力水平，可檢測效應量應相等。所以越接近真實效應量的值越代表能拒絕零假設。另外，用基于標準差觀測值來計算可檢測均值差異也是不可取的，因為我們也應考慮到標準差的變異性。

在研究完成之后再修改統計檢驗力是很難的，后驗檢驗力分析永遠不可以代替事前分析。盡管對于事后分析的結果有時會有誤解，但是如果研究者可以正確解釋該結果，那么對未來的研究是非常有利的，例如研究者可能得出使用不同的顯著性水平更加合適（用0.05而不是0.01）或者發現整個實驗設計存在缺陷而需要重新設計。

3.3?存在的問題

在研究者為復雜實驗設計做統計檢驗力分析時可能會遇到一些實際問題。第一，當研究中的自變量有多組時，需要調整顯著性水平來控制整體第一類錯誤率。例如如果使用Holm-Bonferroni方法來控制第一類錯誤率，那么統計檢驗力分析則變得復雜起來。Holm-Bonferroni矯正會導致第二類錯誤增多，因為隨著對比對數的增多，統計檢驗力會降低。例如如果我們需要對比5組，即共有10組對比，當設顯著性水平為0.05時，即第一類錯誤率為0.05，在Holm-Bonferroni矯正之后，α=0.005，可能導致第二類錯誤率升高。

第二，當模型很復雜時沒有統一的方法做出相應的統計檢驗力分析。例如在混合線性模型（linear mixed model）中，相對來說固定效應（fixed effects）的統計檢驗力分析比隨機效應（random effects）或者固定效應與隨機效應混合在一起時要容易分析。并且若考慮到交互作用或協方差，模型會變得更加復雜。然而變量之間的交互對研究者非常重要，但是在統計檢驗力分析軟件中又很難把這一部分添加進去，所以一個可以用來做統計檢驗力分析的通用且準確的方法是很重要的。

第三，統計檢驗力分析的結果無法泛化。一旦實驗的研究方法、實驗設計或者統計方法改變，統計檢驗力分析就需要重新計算。并且通過檢驗力分析所得的樣本量為理論上可行樣本量，但針對某些特定統計方法或實際情境，此樣本量可能并不夠，例如邏輯回歸分析（logistic regression analyses）就需要非常大的樣本量，研究者在實驗開始之前通過相應的統計檢驗力分析來確定的樣本量對于邏輯回歸分析而言可能依然不夠。如果樣本量不夠，由此而得的研究結論則不可信。所以在統計檢驗力分析之外，研究者也需要考慮到現實因素。另外，因為統計檢驗力分析是建立在一些假設和猜想上的，且考慮到缺失值的問題，研究者采用的樣本數應該比計算而得的樣本數在合理范圍內稍大。

第四，用來計算統計檢驗力的軟件也存在一些問題：（1）可以用來計算統計檢驗力的軟件有限，通常使用的只有： SamplePower， GPower， PASS， SAS， R和Optimal Design;（2）這些軟件大部分都比較昂貴，盡管有的大學提供使用密鑰，但是對于老師學生以及很多研究者來說還是無法方便地使用;（3）有一些軟件不具備在復雜實驗設計下簡便計算統計檢驗力的能力，并且無法在模型中加入交互作用;（4）這些軟件可以進行的統計檢驗力分析類型有限，例如計算多層次統計檢驗力可以用Optimal Design或者PASS，選擇并不多，但前者只有Windows版本，而后者又相當之昂貴。這些因素都限制了統計檢驗力分析的應用與普及。

4?多層模型統計檢驗力分析及Optimal Design實現

多層模型，顧名思義涉及到多個層次的數據，例如研究者研究在某一大學中使用幻燈片教學是否對大一學生的數學學習有幫助這一問題，收集到的數據可以分為不同的層次。學生的年齡、性別、數學成績等都是學生本身的變量，而專業的規模、男女比例、教學所使用教學樓的地理位置等是專業層次的變量，再往高層次來看，學校的規模、地理位置、是否為211或985等因素為學校層級的變量。如此數據在多層模型中發生了嵌套。多層模型分析方法很多，本文著重統計檢驗力的分析方法。在此以包含一個隨機截距和一個隨機斜率的多層線性回歸模型為例來展示檢驗力分析的過程：

假設研究者研究在某一大學中使用幻燈片教學是否對于大一新生的數學學習有幫助這一問題，大一新生被隨機分配在實驗組（使用幻燈片教學）或者控制組（不使用幻燈片教學），研究者設定實驗區塊（block）為不同學生所學的不同專業。因此，在每一個專業中，新生會隨機分配到使用或不使用幻燈片教學的班級中。

如果不考慮協變量，模型使用Raudenbush和Bryk（1992）注釋為：

下面使用Optimal Design（Radudenbush， 2011）來展示多層次統計檢驗力的過程。首先利用此軟件及模型可以計算在研究者期望達到的統計檢驗力水平下所需的樣本量。其所需要設定的參數有：（1）顯著性水平（α=0.05）;（2）預期統計檢驗力（β=0.80）;（3）樣本量/簇大小（待決定）;（4）被協方差解釋的方差大小（R2）;（5）被區塊解釋的方差大小（B）;（6）效應量（Δ）;（7）效應量變異性（σ2）。

假設研究者預期使得專業為區塊可解釋40%的結果的變異性，如果使用一個隨機效應模型且將效應量變異性設定為0.05時（如果研究者使用的是固定效應模型，效應量變異性應設定為0），并且在先前設定信息的基礎上，假如基于試驗研究，研究者預期使用幻燈片的學生比不使用幻燈片的學生的表現要好0.2個標準差單位，也就是說設定效應量為0.2。所以，當研究者想在達到0.8的統計檢驗力并且從每一個專業挑選30個學生的情境下能探測到此效應量時，他們一共需要多少個專業？選擇Person randomized trials → multisite（blocked） trials → Power on y axis → power vs. total number of sites（J），將已設定的參數輸入Optimal Design，基于圖2，可以看出需要28個專業，即一共需要840個被試。

如果考慮協變量，假設基于一個基線調查（baseline survey）（例如IQ，SAT， ACT 等的測量），前測（pretest） 可以解釋結果的60%的變異性，如果我們把協變量（IQ）也包括在模型里，可計算得一共需要19個專業（圖3），即一共需要570個被試，比不包括協變量時少了270個被試，此模型為：

其中假設IQ可解釋學生數學成績中60%的變異性。

其次，使用Optimal Design還可以計算效應量。例如，設定前測可以解釋結果的60%的變異性，如果研究者只能從15個專業中選取被試，并且每個專業選取30人，那么如果想要達到0.8的統計檢驗力至少需要的效應量是多大？在Optimal Design中需設定的參數為：（1）顯著性水平（α=0.05）;（2）預期統計檢驗力（β=0.80）;（3）樣本量/簇大小（15個專業，每個專業選取30人）;（4）被協方差解釋的方差大小（R2）;（5）被區塊解釋的方差大小（B）;（6）效應量（Δ）（待計算）;（7）效應量變異性（σ2）。

在Optimal Design中選擇Person randomized trials→multisite（blocked） trials→MDES on y-axis→MDES vs. number of clusters（J）。 當只能從15個專業中選被試時， 效應量大約為0.29（圖4）。 如果在此分析中考慮協方差， 效應量大約為0.23（圖5）。

5?總結與建議

統計檢驗力分析是科學研究中重要的組成部分，在研究開始之初，統計檢驗力分析可以指導研究者確定研究樣本量以達到不同的效應量或統計檢驗力要求。在研究完成之后，統計檢驗力分析可以幫助研究者印證或審視顯著或不顯著的研究結果，進而指導研究者不拒絕零假設或者再增加被試量進行進一步的研究。

在本科階段，所使用的教材中假設檢驗相關章節已非常普及，但與此相關的統計檢驗力分析、效應量分析等知識章節并不常見，與此相關的教學也并不普及，有一些老師在教學過程中加入此方面相關知識，但講解也并不深入。學生往往只知當p值在小于0.01或者0.05時拒絕零假設，說明不同實驗處理之間存在顯著差異，或當p值大于設定的顯著性水平時不拒絕零假設，說明不同實驗處理之間不存在顯著差異。但更進一步，學生不知如何解釋p值、置信區間、統計檢驗力和產生研究結果的原因。之后碩士及博士階段，隨著科研難度及數量的增加，如果研究者不了解統計檢驗力分析相關知識可能會在研究開始之前無所適從，例如究竟需要多少被試呢？在這種情況下，往往研究者會在未設定樣本量的情況下開始實驗，直到研究結果顯著時停止收集數據，從而影響研究結果的可靠性。因此，從教學上來說，從本科階段開始，要逐步普及統計檢驗力分析的重要性及方法，為日后科研工作做出鋪墊。

在研究過程中，研究者應謹慎、正確地進行統計檢驗力分析。它可以幫助科研人員確定樣本量的大小，從而避免人力物力的浪費，也可以在一定被試量下得出統計檢驗力的信息，例如，如果只有75個可用的被試，而所得統計檢驗力非常低，則沒有必要進行這樣的研究。在論文發表時或者科研基金申請時，通常都要求研究者說明統計檢驗力的相關信息，統計檢驗力的高低雖不是判斷研究好壞的唯一標準，但是高的統計檢驗力是使得研究結論可靠的重要的一方面。

參考文獻

溫忠麟， 范息濤， 葉寶娟， 陳宇帥（2016）. 從效應量應有的性質看中介效應量的合理性. 心理學報， 48（4）， 435-443.

吳艷， 溫忠麟（2011）. 與零假設檢驗有關的統計分析流程. 心理科學， 34（1）， 230-234.

鄭昊敏， 溫忠麟， 吳艷（2011）. 心理學常用效應量的選用與分析. 心理科學進展， 19（12）， 1868-1878.

Aguinis， H.， Pierce， C. A.， & Culpepper， S. A.（2009）. Scale coarseness as a methodological artifact： Correcting correlation coefficients attenuated from using coarse scales. Organizational Research Methods， 12（4）， 623-652.

Altman， D. G. & Royston， P.（2006）. The cost of dichotomising continuous variables. BMJ， 332（7549）， 1080.

Raudenbush， S. W & Bryk， A. S.（1992）. Hierarchical linear models： applications and data analysis methods. Chicago， IL： Sage.

Coe， R.（2002）. Its the effect size， stupid： what effect size is and why it is important. Retrieved May 25， 2018， from： https：//www. leeds. ac. uk/educol/documents/00002182. htm.

Cohen， J.（1988）. Statistical power analysis for the behavioral sciences. Hillsdale， NJ： Lawrence Erlbaum Associates.

Cohen， J.（1992）. A power primer. Psychological Bulletin， 112（1）， 155-159.

Hoenig， J. M.， & Heisey， D. M.（2001）. The abuse of power： the pervasive fallacy of power calculations for data analysis. The American Statistician， 55（1）， 19-24.

Howell， D. C.（2017）. Fundamental statistics for the behavioral sciences. Boston， MA： Cengage Learning.

Lenth， R. V.（2001）. Some practical guidelines for effective sample size determination. The American Statistician， 55（3）， 187-193.

Lipsey， M. W.， & Wilson， D. B.（1993）. The efficacy of psychological， educational， and behavioral treatment： Confirmation from meta-analysis. American Psychologist， 48（12）， 1181-1209.

Maxwell， S. E.， Delaney， H. D.， & Kelley， K.（2018）. Designing experiments and analyzing data： A model comparison perspective. New York： Routledge.

Perugini， M.， Gallucci， M.， & Costantini， G.（2018）. A Practical primer to power analysis for simple experimental designs. International Review of Social Psychology， 31（1）， ?1-23.

Raudenbush， S. W.， et al.（2011）. Optimal Design Software for Multi-level and Longitudinal Research. Retrieved May 21， 2018， from http：//www. wtgrantfoundation. org.