借助數形橋梁把握認數本質

俞麗春

“小數的初步認識”是學生第一次在課堂上正式接觸小數。在教學時，為了能讓學生更好地理解小數的含義，體會小數的現實意義，教師應力求準確把握學生的認知起點，借助數形結合思想，以具體形象作為支撐，把抽象的數學概念簡單化、形象化，促進學生理解概念的本質，感受到數學之趣。

一、喚起經驗，引出小數的教學

小數概念教學是小學數學教學中的核心內容之一，對于小數概念的教學，應基于學生的已有知識和經驗，通過師生的交流互動，喚起學生的經驗世界，從而豐富學習的內容。

教學伊始，筆者先讓學生回憶一下都認識了哪些數？學生一下就想到了整數和分數，筆者借機復習了整數和分數的概念，又接著追問：“除了整數和分數，在生活中，你還見到過什么數？在哪見過？”個別學生馬上想到了小數，并指出超市里的商品價格是小數。筆者順勢出示事先準備的商品價格單來引出課題，并提出：“這些小數，怎么讀，怎么寫呢？”

在此過程，從數的復習開始，喚起學生的已有知識和經驗，并順其自然地引出了新知識——小數。這樣基于學生生活經驗的引入，讓學生倍感親切、自然，讓學生初步感受小數與生活的密切聯系，體會小數的現實意義。通過“怎么讀？怎么寫？”這樣簡單的提問，直接引入了小數的讀寫知識，也為后續更好地幫助學生理解小數的意義打下基礎。

二、新舊結合，以形助數，感悟小數的含義

小數是比較抽象的數學概念，為了激起學生學習興趣，可以巧借學生已有的經驗，并合理地借助直觀圖形將抽象的認數知識轉化為直觀、易懂的圖形知識，讓數形結合思想在小數教學中滲透。

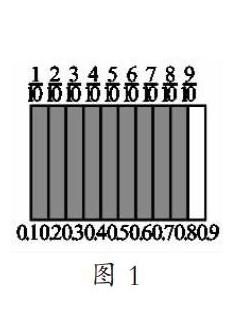
筆者引導：“我們在認識人民幣的時候，知道1元等于幾角？”，學生異口同聲回答：“10角。”筆者接著出示一個正方形，問：“如果一個正方形表示人民幣1元，10角就是要把這個表示1元的正方形平均分成多少份？2角又是其中的幾份？用分數表示是幾分之幾元呢？”經過層層的以問引學，讓學生知道因為1元等于10角，所以把表示1元的正方形平均分成10份，取其中的2份是元，也就是2角，還可以是02元。接著筆者又提出：“1角、4角用小數表示是多少元？并說明想法。”有了剛才的引導，大部分的學生都能很好地表述自己的想法。筆者接著問學生，在正方形中，還能找到哪些相應分數和小數？學生們一下就找到了01至09相應的分數和小數（見圖1），筆者接著要求學生認真觀察正方形圖，并讓他們輕聲讀一讀相應分數和小數，想想有什么發現？通過學生的觀察、思考和交流，他們發現十分之幾就是零點幾，零點幾就是表示十分之幾，這些都是很有價值的發現。

小數教學的重點就是要突出理解數的含義，筆者充分利用學生的已有生活經驗，通過“以元作單位的小數轉化為角，幾角就是零點幾元”的生活經驗出發，引出02元就是2角，再以“1元等于10角，幾角就是十分之幾”為教學起點，喚醒學生對分數的記憶，建立分數與小數的聯系。在后續的教學中，借助直觀圖，學生說、找相應分數和小數就顯得游刃有余。通過將生活經驗與課堂知識的結合，以形助數的處理方式，不僅讓學生體會到分數與小數的內在聯系，還能突出新知識的生長點，幫助學生提升知識遷移能力，有效地突破“認識一位小數”的教學難點。

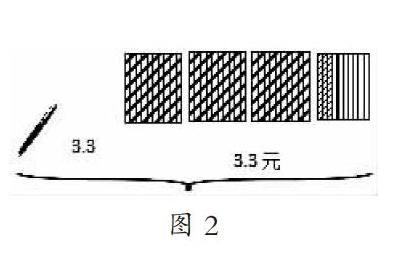
接著，筆者讓學生以對應01、對應02這樣的方式讀數，直到對應09，并通過多媒體演示把涂色為09的正方形，繼續涂滿出現1，筆者借機指出：這就是小數零點幾與自然數1之間微妙的關系。筆者接著出示兩個平均分成10份的正方形，一個涂滿顏色，一個涂其中的2份，合起來表示一本筆記本的價格，筆者提問：“一本筆記本的價格是多少元呢？會用小數表示嗎？”學生一下就知道用1.2元表示，并能說明理由;接著出示鋼筆的價錢，讓學生說明兩個“3”的含義，并用正方形圖表示出鋼筆的價錢（見圖2）。

在這個教學過程中，筆者借助直觀手段，讓學生初步體會10個0.1就是1，滲透滿十進一的計數方法，再借助圖形“1個正方形涂滿就是1元”，以12元和33元為例，不斷豐富學生對小數的體驗，從而讓學生輕松自然地認識整數部分不是0的一位小數。

三、借形思數，深化小數的本質

在練習提升部分，筆者通過課件演示先把正方形變成一把米尺，讓學生在米尺上找小數;再把米尺變成線段，讓學生在線段上找小數;又把線段向兩邊伸展變成數軸，讓學生在數軸上找到筆者說出的幾個點，并要求結合圖說明理由。筆者接著又提出：“在數軸看得見的地方，能找到小數，看不見的地方，還能找到小數嗎？”學生滔滔不絕，舉了很多的小數，并發現有說不完的小數。

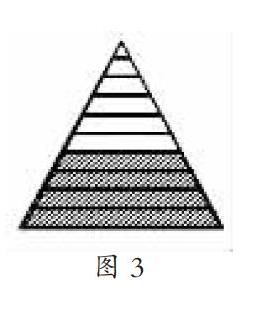
在總結延伸部分，筆者借助課件演示，讓學生回顧學習過程，并提出：“在正方形、尺子、線段、數軸這些圖形中，為什么圖形一直在變化，都還能找到同一個小數04呢？”學生有的說都是把圖形平均分成了10份，04表示其中的4份;有的說零點幾的小數，和圖形的形狀沒有關系，只要把這個圖形平均分成10份，取其中的若干份。最后筆者出示一個部分涂色的三角形（見圖3），并提問：“取出其中的4份，能用04來表示嗎？”學生異口同聲：“不能，因為它沒有平均分成10份。”對于學生的回答，筆者給出小結：把圖形平均分成10份，取其中的若干份，用零點幾表示，這才是小數最根本的性質。

在這一環節，筆者借助圖形的演變，由具象到抽象逐漸變化直觀圖，在一定程度上幫助學生充實對小數的認識;為學生提供了主動思考的機會及較大的思維空間，有利于學生主動獲取知識，使學生體驗和感受數學概念發現的過程，進一步讓學生在思維中構建起“分數與小數的內在聯系”，對小數概念本質的理解和把握也越清晰，同時為培養數感創造了有利條件，也為后面學習小數的大小比較作了方法上的孕伏。

總之，準確把握認識起點，巧借經驗，架起數與形的橋梁，不僅可以幫助學生直觀了解數，而且有利于培養學生的抽象思維能力，同時促進深化小數的本質，使思維轉向更高級、更抽象的形式。

（作者單位：福建省霞浦縣教師進修學校 責任編輯：王振輝）