一類具有非線性發生率和治愈率的SEIRS模型研究
高雪麗, 王 輝, 胡志興
(北京科技大學 數理學院,北京 00083)
引 言
傳染病是危害人類身體健康的重要疾病。在控制和消除傳染病過程中,治療是預防和控制各種傳染病傳播的重要方法。在經典的流行模型中,被認為治愈率與感染個體的數量成正比[1]。在一些疾病挑戰了正常公共衛生系統和能力之后,研究人員開始從建模和分析的角度來考慮醫療保健系統的能力[2]。Wang和Ruan認為,在一個社區中,治療疾病的能力是恒定的[3]。Wang提出了以下分段函數[4]
(1)
在SEIRS模型中,其中k是治愈率,這意味著當治療能力還沒有達到極限時,治療能力是與感染者的數量成比例的,否則將采用治療能力的極限值常數形式作為治療函數。治愈函數(1)已經在一些文獻中得到了應用[5-7],其他的治愈函數也被提出,并應用在許多文獻中,例如飽和治愈率T(I)=rI/(1+μI),r>0,μ≥0[8-10]。
本文主要考慮了在有限資源的情況下公共衛生系統對病人的治療能力,這可能發生在很大一部分情況下,比如患者人數較多,但醫療設施不足、床位數量有限等,應用了分段函數(1)作為治愈函數。又在模型中應用了飽和發生率[11],并考慮了恢復者再次喪失免疫變為易感者[9]。建立了飽和發生率和分段函數治愈率的SEIRS傳染病模型。
1 傳染病模型的建立
建立以下易感者—潛伏者—病染者—恢復者—易感者(susceptible-exposure-infected-recovery-susceptible)傳染病模型:
(2)

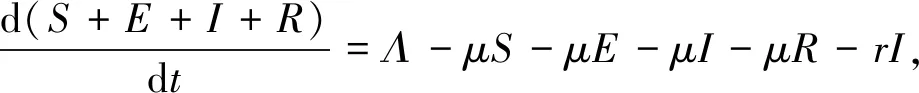
2 平衡點的存在性
設系統(2)的正平衡點為I*,當0 (3) 當I*>I0時,使系統(2)右邊得零,可得 (4) 由系統(3)可得基本再生數 (5) 經計算可得當R0>1時,系統(3)有唯一的地方病平衡點P*(S*,E*,I*,R*),其中 (6) (7) 同時式(6)中的I*必須滿足I*I0,即可得 (8) 由系統(4)可以得到I*必須滿足如下方程 b0(I*)2+b1I*+b2=0, (9) 其中 b0=(ψ+μ)(μ+σ)(β+bμ)(μ+r+θ)-βψσθ, (10) (11) 由式(10)可以得到 (12) 其中 a1=b(ψ+μ)(μ+σ)+(μ+σ+ψ)β; a2=(ψ+μ)[βσΛ-(μ+σ)μ(μ+r+θ)][b(ψ+μ)(μ+σ)+(μ+σ+ψ)β]>0; a3=[(ψ+μ)(μ+σ)(β+bμ)(μ+r+θ)-βψσθ](ψ+μ)(μ+σ)>0; a4=(ψ+μ)[(μ+σ)μ(μ+r+θ)-βσΛ]。 由式(12)的二次方程便可以得判別式 (13) 或 (14) 當(σ+μ)μ(μ+r+θ)<βσΛ時,可得u0 因此當且僅當(σ+μ)μ(μ+r+θ)<βσΛ,uu0時b1<0,Δ≥0。 假設b1<0,Δ≥0,則式(9)有兩個正根I1,I2, (15) 則 如果Ij>I0,則Pj(j=1,2)是系統(2)的一個地方病平衡點。 u (16) 其中 l1=2[(ψ+μ)(μ+σ)(β+bμ)(r+μ+σ)-βψσθ]+kμ[b(ψ+μ)(μ+σ)+(μ+σ+ψ)β]。 也等價于(2b0I0+b1)2-Δ>0,經過計算可以得出 于是可得 (1)如果(σ+μ)μ(μ+r+θ)<βσΛ(σ+μ)μ(μ+r+θ+k)則可以得到(b1+2b0I0)2-Δ>0。 (2)如果βσΛ>(σ+μ)μ(μ+r+θ+k),則R0>1;(b1+2b0I0)2-Δ>0等價于u>u2。 因此可得當且僅當 1)u 2)u 其中k1=μ(μ+σ)(μ+r+θ);k2=(ψ+μ)(μ+σ)(μb+β); l2={2[k2(r+μ+θ)-βψσθ]+kμ[b(ψ+μ)(μ+σ)+(μ+σ+ψ)β]}(μ+σ)μ(k+μ+r+θ)。 同理可以計算在I2存在時,滿足I2>I0的條件,可以用反證法。 我們即得到當I2>I0時,當且僅當 1)u 2)uu0,u 歸納總結以上討論分析,有文獻[7]中類似的結論。 定理2.1當(σ+μ)μ(μ+r+θ)≥βσΛ或u>u0時,系統(2)的地方性平衡點P1,P2都不存在,我們假設(σ+μ)μ(μ+r+θ)<βσΛ,uu0,于是有下面結論。 1)當R01,u 推論2.2 1)當R0<1,(σ+μ)μ(μ+r+θ)<βσΛ,且umin(u0,u1)時,地方病對平衡點P1,P2存在,則系統(2)關于地方病平衡點存在一個后向分支。 定理2.3 2)當且僅當R0>1,u≥u2,系統(2)的地方病平衡點P*(S*,E*,I*,R*)存在進一步當u>u0或u1 證明由式(14)得u>u0意味著Δ<0,則此時P1,P2都不存在。當u1 由文獻[7]的定理3.1的證明過程可證系統(2)的無病平衡點P0局部漸近穩定性和全局漸近穩定性。 定理3.1當基本再生數R0<1時,無病平衡點P0局部漸近穩定;當R0>1時,無病平衡點P0不穩定;進一步,當R0<1,u>u0時,P0為唯一的平衡點。 證明無病平衡點P0處的雅克比(Jacobian)矩陣為 (17) 特征方程為 (λ+μ)(λ+μ+ψ)[(λ+μ+σ)(λ+k+μ+r+θ)-βσΛ/μ]=0 λ1=-μ<0,λ2=-(μ+ψ)<0, λ3+λ4=-(2μ+σ+r+θ+k)<0,λ3λ4=(μ+σ)(k+μ+r+θ)(1-R0)。 當R0<1時,λ3+λ4<0,λ3λ4>0時可得特征根都為負值,即無病平衡點P0是局部漸近穩定;當R0>1時,λ3+λ4<0,λ3λ4<0,即λ3,λ4異號,特征根存在正值,便得無病平衡點P0是不穩定。 推論3.2當R0<1時,地方病平衡點P*不存在;若u>u0,則地方病平衡點P1,P2也不存在;則R0<1時無病平衡點P0是系統(2)的唯一的平衡點。 定理3.3如果系統(2)的地方病平衡點P*存在,則P*是局部漸近穩定的。 證明地方病平衡點P*處的雅克比(Jacobian)矩陣為 可得特征方程為 λ4+A1λ3+A2λ2+A3λ+A4=0。 其中 可得Ai>0(i=1,2,3,4), 由Hurwitz判據得特征方程的所有根都具有負實部,所以當R0>1,u≥u2,地方病平衡點P*是局部漸近穩定的。 由文獻[7]的定理3.4的證明方法可證得地方病平衡點P1是不穩定的。 定理3.4如果系統(2)的地方病平衡點P1存在,則P1是不穩定的 證明地方病平衡點P1(S1,E1,I1,R1)處的雅克比(Jacobian)矩陣為 便可得 所以可得特征方程的根是異號的,一定有正根存在,由Hurwitz判據得地方病平衡點P1是不穩定的。 由文獻[8]的命題2的證明方法可證系統(2)的地方病平衡點P2在一定條件下是局部漸近穩定的。 定理3.5如果系統(2)的地方病平衡點P2存在,則P2是局部漸近穩定的。 證明地方病平衡點P2(S2,E2,I2,R2)處的雅克比(Jacobian)矩陣為 可得特征方程為 λ4+d1λ3+d2λ2+d3λ+d4=0, 令 d1=μ+x1+x3+x4+x5; d2=(μ+x1)(x3+x4)+x3x4+(μ+x1+x3+x4)x5-σx2; d3=[(μ+x1)(x3+x4)+x3x4-σx2]x5+(μ+x1)x3x4-σx2(x5+μ); d4=-ψσθx1+(μ+x1)x3x4x5-σx2μx5。 令 m1=μ+x1+x3+x4;m2=(μ+x1)(x3+x4)+x3x4; m3=(μ+x1)x3x4;m4=-ψσθx1。 可得 Δ1=d1=m1+x5>0, =(μ+x1+x3+x4+x5)](μ+x1)(x3+x4)+x3x4+(μ+x1+x3+x4)x5-σx2] -[(μ+x1)(x3+x4)+x3x4-σx2]x5-(μ+x1)x3x4+σx2μ>0, =(m1-μ)(μ+x5)(σx2)2+{(μ-m1+x5)(m2x5+m3)-(m1+x5)(m2+m1x5)x5- m3](m2x5+m3)-(m1+x5)2(m3x5+m4), Δ4=d4Δ3。 由Hurwitz判據得只要Δ3的符號就可判定地方性平衡點P2的局部漸近穩定性。記 σx2=y; n1=(m1-μ)(μ+x5) n2=(μ-m1+x5)(m2x5+m3)-(m1+x5)(m2+m1x5)x5- n3=[(m1+x5)(m2+m1x5)-m2x5-m3](m2x5+m3)-(m1+x5)2(m3x5+m4), 便可得 Δ3=n1y2+n2y2+n3, 顯然n1>0,n3>0。則得到P2的局部漸近穩定性的充分性條件,其可以看作是以y為變量的二次函數,顯然m1>0,則得到Δ3>0的充分條件,也就得到地方病平衡點P2(S2,E2,I2,R2)的局部漸近穩定的充分條件。 (1)當Δ>0,如果y (3)當Δ<0,對于任意的實數y,地方性平衡點P2是局部漸近穩定的,其中 這一部分將選取一系列的參數通過MATLAB數值模擬畫出相應的圖形,驗證本文的結論,以便更直觀地得到平衡點的穩定性。 對于系統(2),選取參數β=0.05,μ=0.03,ψ=0.3,b=0.1,σ=0.15,r=0.3,θ=1,Λ=3,k=3.5。通過計算可得R0=0.8627<1,u0=1.2690,u1=2.5210,即為定理2.1的情況1。如圖2所示會出現一個后向分支,圖中的一條直線表示無病平衡點P0,既當0 對于系統(2),選取參數β=0.05,μ=0.03,ψ=0.3,b=0.1,σ=0.15,r=0.3,θ=0.8,Λ=5.5,k=3.5。通過計算可得R0=0.8627<1,u0=1.2690,u1=2.5210,如圖2所示系統(2)會出現一個后向分支。選擇I0=0.29,u=1 2.1 地方病平衡點P*(S*,E*,I*,R*)的存在性

2.2 地方病平衡點P1(S1,E1,I1,R1),P2(S2,E2,I2,R2)的存在性
b1=(ψ+μ)[(μ+σ)μ(μ+r+θ)-βσΛ]+uμ[b(ψ+μ)(μ+σ)+(μ+σ+ψ)β],
b2=(ψ+μ)(μ+σ)uμ。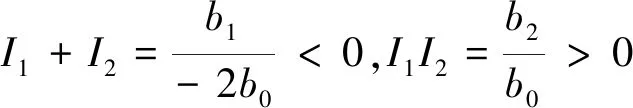
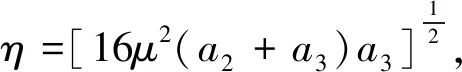

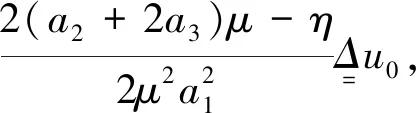


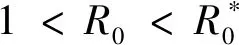





3 平衡點的穩定性

4 數值模擬








5 結 論