臨床試驗隨機化方法的優選

袁陽丹 劉甜甜 劉玉秀,3△ 陸夢潔 周憧憧 陳 羽 劉雅琦

1.南方醫科大學公共衛生學院生物統計學系(510515) 2.中國人民解放軍東部戰區總醫院醫學統計學教研室 3.南京醫科大學公共衛生學院生物統計學系

【提 要】 目的 近十幾年來涌現出一些新的隨機化方法，能有效提升隨機化的性能，但其在臨床試驗中真正應用的情形并不多見，仍然以傳統的區組隨機化設計占據主導，存在著嚴重的潛在選擇性偏倚風險。本研究將通過探討多種隨機化方法的統計性能，為臨床試驗隨機化方法的選擇提供實用性指引。方法 選擇簡單隨機化設計(SR)方法，以及目前常見的五種限制性隨機化方法，包括固定區組設計(PBD)、變化區組設計(VBD)、大棒設計(BSD)、帶不平衡限制的偏幣設計(BCDWIT)、區組甕設計(BUD)，借助隨機模擬方法，在不同的最大容許不平衡性(MTI)設定下，分別從隨機性和均衡性兩個方面對各方法的統計性能進行整體評價。本研究涉及的隨機化方法優選僅在限制性隨機化方法中進行，并將各方法的隨機化性能指標作為評價優選的依據。結果 PBD和VBD方法的固定分配概率、猜對分配概率最高，相比之下，BSD、BUD 、BCDWIT方法具有更好的隨機化性能。具體看， BUD有著最小的固定分配概率，BCDWIT其次；BSD有著最小的猜對分配概率，BUD其次。結論 為了減少試驗的選擇性偏倚，區組隨機化設計不應再作為開放性臨床試驗隨機化的推薦方法，而應考慮在其他幾種限制性隨機化方法中進行選擇。在隨機化方法選定后，還可通過大量模擬篩選出最佳的隨機分配序列。

近年來，因區組隨機化設計(block design)較高的固定分配概率和猜對分配概率，而產生的較大選擇性偏倚風險，備受學術界質疑和關注。Berger 多次強烈建議區組隨機化不應該再被使用[1-4]。為了克服區組隨機化的確定性特征，一些學者提出了多種其他方式的限制性隨機化方法。例如，Soares和Wu提出了大棒法(big stick design，BSD)[5]；Chen提出了帶不平衡限制的偏幣設計(biased coin design with imbalance tolerance，BCDWIT)[6]；Zhao等人提出了區組的甕式設計(block urn design，BUD)[7]。

本文將針對兩處理組的情況對多種隨機化方法進行多指標的比較，探討多種隨機化方法的統計性能差異，為臨床試驗隨機化方法的選擇提供實用性的建議和指引，以降低因隨機化而導致的臨床試驗質量減損。

隨機化方法性能評價指標

隨機化方法的性能通常從均衡性和隨機性兩個方面來進行綜合評價。然而，研究表明在大樣本的情況下(例如大于200)，因不均衡所導致的把握度損失不大[8]，因此對于帶有較強的均衡性限制條件，例如限定最大容許不平衡性(maximal tolerated imbalance，MTI)在一定范圍的限制性隨機化方法而言，并不會出現嚴重的不均衡，通常可以忽略對均衡性的考量，而將重點放在隨機性指標的評價上。

1.均衡性評價指標

常用的均衡性指標有3個，分別是：分配過程中組間受試者例數差的最大值(the maximum absolute imbalance in the randomization sequence，MI)、組間例數分配相等的概率(the probability of achieving exact balance in the randomization sequence，EB)以及組間例數差的絕對值均數(the absolute mean of the difference in treatment group sizes，DN)。當試驗為了避免因受試者入組時間不同而導致偏倚時，需要考慮MI指標。EB指標在實際應用中較為少見，在一些大樣本的臨床試驗中更為少見。當組間例數的不均衡受樣本量影響時，DN就顯得較為重要。

2.隨機性評價指標

常用的隨機性指標有固定分配概率(deterministic assignment，DA)和猜對分配概率(correct guessing，CG)。其中，固定分配概率表示受試者被分配到某一組的概率為1或0的次數占總分配次數的比例，猜對分配概率指按照分配到例數少的組猜測并且猜對的比例。

指標CG由Blackwell和Hodges兩位學者于1957年提出[9]，其公式如下：

(1)

其中：

(2)

Ti表示第i例受試者的分配結果，ni-1,1和ni-1,2分別表示第i-1例受試者完成隨機分配以后組1和組2的分配例數。

這兩個指標是將隨機性進行量化的指標，其值越小表示隨機性越高。

幾種隨機化方法的分配概率

1.簡單隨機化方法

簡單隨機化(simple randomization，SR)在分配過程中能保證受試者分配到任意一組的概率都為0.5，簡單隨機化的條件分配概率為：

(3)

2．區組隨機化方法

固定區組隨機化設計(permuted block design，PBD)在實際應用中使用較為普遍，設其區組長度為b，其條件分配概率為：

(4)

變化區組隨機化設計(variable block design，VBD)，首先確定擬變化的區組個數及其長度，然后在其中隨機選擇，之后按照選定的區組再隨機分配。

3．BSD方法

BSD方法是由Soares和Wu等人在1983年提出的一種僅限于兩處理組平衡試驗的隨機化方法，其主要思想是通過設置MTI來控制處理組間的不均衡性。MTI指兩組例數相差最大能允許的例數上限。其條件分配概率為：

(5)

其中di-1表示第i-1例受試者分配之后，兩處理組例數之差，即ni-1,A-ni-1,B；后同。

4．BCDWIT方法

BCDWIT方法是由Chen在1999年提出的一種隨機化方法，該方法是在Efron的偏幣法的基礎上加入了MTI限制，以保證處理組間具有足夠的均衡性，該方法也可以認為是升級版的BSD方法，它在BSD的基礎上添加了調整概率Pbc(在0.5至1之間取值)。BCDWIT方法的條件分配概率為：

(i=1,2,…,n)

(6)

BCDWIT的條件分配概率不僅與MTI有關，與調整概率Pbc也存在一定的關系。當調整概率為0.5時，該方法即BSD方法，隨著Pbc增大，組間的均衡性改善。但是調整概率過大，容易根據以往的分配猜測出當前分配結果。有文獻研究表明，偏幣法的調整概率設為2/3，既能保證一定的組間均衡性，又能確保一定的隨機分配結果的不可預測性[8]。

5．BUD方法

BUD方法是由Zhao和Weng兩人在2011年提出的替代區組隨機化的一種方法。該方法結合區組隨機化和甕模型來達到隨機分配的目的，不僅適用于兩組平衡試驗，還可用于多組或不平衡試驗。BUD方法簡單易操作，其條件分配概率為：

(7)

幾種隨機化方法的統計性能模擬比較

1．模擬方法

針對前面提到的多種隨機化方法，為了比較各方法的統計性能，我們首先對不同方法的隨機性和均衡性進行評價，MTI設置為2，對SR、PBD、BSD、BCDWIT、BUD以及VBD(VBD方法選定區組長度為4和6兩種區組)這6種方法，選定樣本量50、100、300、500和800進行模擬。在同樣的樣本量設定下，我們又另外對PBD、BSD、BCDWIT、BUD這4種限制性隨機化方法進行模擬比較，區組長度分別取2、4、6、8、10、12、14、16共8種情況，相對應的MTI值分別為1、2 、3、4、5、6、7、8。BCDWIT方法中的調整概率Pbc取0.667。通過10000次的模擬來評價各個方法的隨機性指標(DA 、CG)和均衡性指標(MI、EB、DN)。本次模擬使用SAS 9.4系統編程實現，分別求出各隨機化方法的評價指標，對各隨機化方法進行多指標比較分析。

2．模擬結果

在上述的模擬情境下，模擬結果顯示，不同樣本量設定時各方法隨機性能指標的統計行為特征類似，為節約篇幅，本文僅給出樣本量為500時的模擬結果。

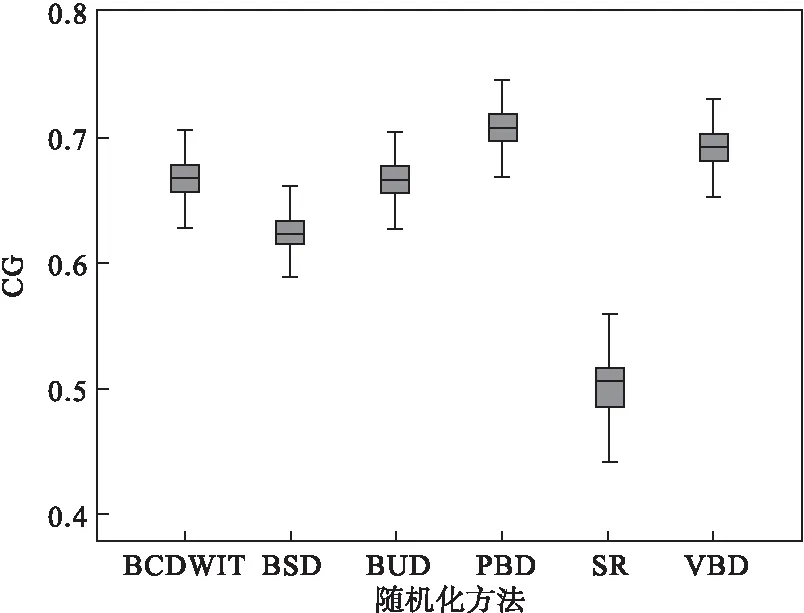
由表1、圖1和圖2可見，在MTI設置為2的條件下，固定分配概率DA由小到大依次是SR

表1 不同隨機化方法各評價指標的模擬比較(MTI=2，VBD區組長度為4和6，樣本量為500，模擬10000次)

由表2、圖3和圖4可見，不同MTI值的情況下，從隨機性指標DA來看，4種方法的DA值都隨著MTI增大而減小，其中BUD的DA值最小，其次是BCDWIT，DA由小到大依次是BUD

圖1 6種隨機化方法隨機性能評價指標DA的模擬比較(MTI=2，VBD區組長度為4和6，樣本量為500，模擬10000次)

圖2 6種隨機化方法隨機性能評價指標CG的模擬比較(MTI=2，VBD區組長度為4和6，樣本量為500，模擬10000次)

盡管均衡性評價對于這里比較的4種隨機化方法并不重要，但為了獲得較為全面的印象，我們還是給出了相應的模擬結果。可見，4種方法的均衡性和限制強度MTI密切相關，MTI越大，均衡性越差。這也提示我們在選擇隨機化方法時對MTI的設定不應太大。

最佳隨機分配序列的遴選

為使隨機化效果更進一步優化，在隨機化方法選定后，還可以通過大量模擬篩選出最佳隨機分配序列，可考慮選擇CG+DA最小的隨機分配序列作為臨床試驗遴選的目標序列。

以BSD方法為例，某臨床試驗隨機分為等比例的兩組，每組50例，設定MTI=2，模擬5000次，得到CG+DA的分布圖見圖5。

BSD方法5000次的模擬中，共挑選出5個最小的CG+DA=0.76的隨機分配序列，以其中2個為例可得到圖6～7。

表2 不同MTI設定下4種限制性隨機化方法各評價指標的模擬比較(樣本量為500，模擬10000次)

圖3 不同MTI情況下4種隨機化方法的DA指標變化情況比較(樣本量為500，模擬10000次)

圖4 不同MTI情況下4種隨機化方法的CG指標變化情況比較(樣本量為500，模擬10000次)

圖5 BSD方法模擬5000次的CG+DA分布圖(樣本量N=100，MTI=2)

圖6 BSD方法模擬5000次中CG+DA最小值的隨機分配序列(CG+DA=0.76,N1=49,N2=51)

圖7 BSD方法模擬5000次中CG+DA最小值的隨機分配序列(CG+DA=0.76,N1=50,N2=50)

結論與討論

在限制性隨機化方法中，PBD和VBD方法均呈現較高的固定分配概率(DA)和猜對分配概率(CG)，使臨床試驗的選擇性偏倚風險增高。為了減少試驗的選擇性偏倚，區組隨機化設計不應再作為開放性臨床試驗隨機化的推薦方法，而應考慮在其他的幾種限制性隨機化方法中進行選擇。從DA看，BUD最小，BCDWIT其次。從CG看，BSD最小，BUD其次。我們認為從臨床實際看 CG 的影響更大， 更傾向于推薦

CG較小的隨機化方法，例如BSD、BUD方法。本研究的結論僅針對開放性臨床試驗的隨機化，對于雙盲設計的臨床試驗，區組隨機化方法并未受到排斥。

人們似乎已經認識到PBD的不足，進而采用VBD來加以改善，甚至將VBD奉為一種隨機化的好方法。從直覺上， VBD的區組變化是隨機的，理應增加預測受試者分組的難度。然而，臨床研究人員預測下一個受試者的分組并不是依據區組大小來判斷，而是猜測分配到受試者例數較少的一組，因此即便不公開PBD區組大小或者VBD隨機變化區組長度，由于猜測的行為規律導致了區組隨機化的性能較低。VBD方法選定區組長度為4和6兩種區組，其隨機性僅稍優于PBD方法，且不如其他3種限制性隨機化方法。

在具體隨機化實施中，為更進一步優化選出最佳隨機分配序列，一旦選定隨機化方法，還可通過大量模擬選出隨機性能最佳(可考慮用CG+DA最小進行選擇)的序列，該機制為提高隨機化的質量提供了很好保證。選擇合適的隨機化方法固然重要，然而，更重要的是做到分配隱蔽，這則另當別論了[10-11]。

本文在以往研究的基礎上，對多種限制性隨機化方法的統計性能進行了探討，完善了隨機化方法學的研究，為臨床試驗隨機化方法的選擇提供了參考，對保證隨機化質量具有重要意義。