思維理解通透，表達方能細致入微
——對一類零點問題的再研究

王子妍

進入高三，在題海中翻滾多年，刷了很多題目，筆者始終感覺雖能得出題目的結果，但在過程的表達上總覺得有些力不從心，離真正的通透還有差距.比如學校第一次周末考試中有這樣一道看似很平常的填空題：

函數f（x）=ex-mx 在（-1，+∞）上沒有零點，求實數m 的取值范圍.

筆者在考試時很快就有了如下的思路：

解令f（x）=0，則ex=mx.

m=0時，等式顯然不成立，此時方程無解，滿足題意.

當x∈（-∞，1）時，h′（x）＞0，h（x）單調遞增；當x∈（1，+∞）時，h′（x）＜0，h（x）單調遞減.

老師對這種方法進行了點評，對于我能對m 是否為0進行討論，為引入連續的函數而把方程變為的形式，進行了表揚，注重細節，轉化合理，但最后老師點明，此類問題江蘇卷前些年大題已有考查，全國卷近兩年的函數導數大題也很青睞這類題目，若把這道題目改為解答題，怎樣才能有規范而精確的表達呢？

課后詢問了老師，以上思路作為解答題是否可行.老師認為做填空題時使用尚可，做解答題還需再想更嚴謹的解法過程.筆者陷入了困惑，怎樣表述才更嚴謹，對于該題，分離變量法的缺陷到底在哪里.

在和同學討論并尋求老師的幫助后，了解到此類問題的缺陷并不是分離變量的問題，而在于x→+∞，h（x）→0這一結論沒有詳實的數學推理過程，最多只是對結果的一個推斷，目前高中數學的知識儲備不足以表達出極限的證明.

筆者和同學們經過討論，形成如下的解題思路：分類討論，并利用函數單調性.

解f（x）=ex-mx，f′（x）=ex-m.

x∈（-1，+∞），f′（x）＞0，f（x）單調遞增.

x∈（-1，lnm]，f′（x）＜0，f（x）單調遞減.

x∈（lnm，+∞），f′（x）＞0，f（x）單調遞增.

當f（lnm）=m-mlnm=m（1-lnm）＞0，即m＜e，則無零點.

老師看完，拋出了一個問題，函數在R上單調遞增，最終增到哪里，是一直趨向無窮大，還是趨向某一個常數，你能用數學語言表達出這種趨勢？

看來還是有缺陷，再次嘗試：

解f（x）=ex-mx，f′（x）=ex-m.

x∈（-1，+∞），f′（x）＞0，f（x）單調遞增.

f（0）=1＞0，f（x）的圖象在[-1，0]上不間斷，則f（x）在（-1，+∞）上有唯一零點，不合題意，舍去.

x∈（-1，lnm]，f′（x）＜0，f（x）單調遞減.

x∈（lnm，+∞），f′（x）＞0，f（x）單調遞增.

①當f（lnm）=m-mlnm=m（1-lnm）＞0，

②f（lnm）=0，即m=e時，則f（x）在（-1，+∞）上有唯一零點，不合題意，舍去.

③f（lnm）＜0，即m ＞e時，

f（0）=1＞0，f（x）的圖象在[0，lnm]上不間斷，則f（x）在（-1，+∞）上有唯一零點，不合題意，舍去.

至此，大功告成，筆者寫完后就已滿意，給老師審閱后，老師也給出了肯定的回復.

反思已知單調性，無法說明一個函數圖象是否“穿過”x軸，再找出一正一負的兩個函數值，結合函數的單調性和連續性，就可以準確表達出“穿過”x軸.

有了這次的探究經歷后，我再接再厲，又研究了如下問題：

分析此題的難度已經比較大了，有了上一題的探索經驗，筆者一開始思路通暢，只在最后的特殊值找尋上頗費了一番精力.

（1）a≤0時，

x∈（0，+∞），f′（x）＜0，f（x）單調遞減.

則f（x）在（0，+∞）上至多有一個零點，不合題意，舍去.

（2）a＞0時，

即a＞e3時，f（x）在（0，+∞）上無零點.

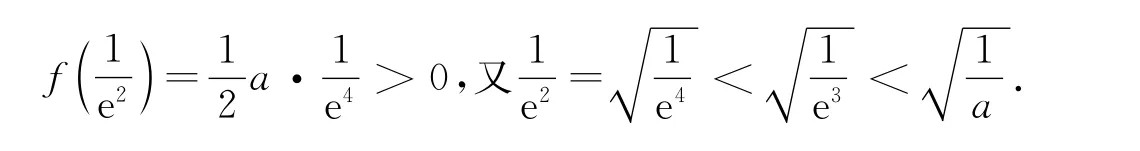
說明在的左側找一個值為什么找這個值？這個值為什么比小？你如何能想到這個值？這些地方都要有清晰的思路，并且能表述清楚.

方法一

說明此方法能把問題表述清楚，當我寫完最后一步時，也著實興奮了好一會兒.仔細回顧一下，這種思路的難點在于這個值很難短時間內想到，筆者也是嘗試了很長時間才找到，但真正考試時，時間有限，肯定沒有這么多的時間去思考.還有沒有其他思路呢？在老師的幫助提示下，我想到了第二種思路：了解一些不等關系式，利用放縮，化為二次函數模型，更有利于取特殊值.

方法二（可由lnx ≤x-1進行放縮，解答題要先證這個不等式，方能使用）

綜上所述，a的取值范圍是a∈（0，e3）.

解決該題雖耗費大量的時間，但我從中收獲了很大樂趣，于是我想進一步鉆研，又請老師提供了類似問題：

函數f（x）=ae2x+（a-2）ex-x.若函數f（x）有兩個零點，求實數a的取值范圍.

難度雖不斷提高，但筆者研究的熱情高漲，通過分析思考，我獨自完成了該題的全部解答過程.有興趣的朋友也可以獨自思考鉆研此題.（該題答案0＜a＜1）

回顧之前的解題歷程，我發現自己對過程的推理不夠重視，許多問題看似能算出正確的結果，但很多過程往往不能表述清楚，有時就似是而非地糊弄過去，真正在考試時遇到難題卻往往不知所措.通過對以上問題的鉆研，筆者真正感覺到，只有真正掌握了數學思想、數學方法的精髓，我們分析問題的思路才能靈活多變，解題過程的表達方能細致入微.

老師點評：答題過程中寫清因果關系，可以提升邏輯推理能力，在考試中遇到解答題也能拿足分數。如果平時注重訓練用數學語言去表達自己的數學思維，那么對一些數學定義、公理、定理等就能有更細致的體會，能形成更嚴謹的數學思維，我們的解題能力和數學思維品質也會得到提高和升華.