可靠性設計優(yōu)化的球空間設計法*

曹魯光，蔡軍亮，王冠坤，陳振中,李曉科,吳子豪

(1.上海機電工程研究所·上海·201109;2.中車大同電力機車有限公司·大同·037038;3.東華大學 機械工程學院·上海·201620;4.河南省機械裝備智能制造重點實驗室·鄭州·450002)

0 引 言

經過近40年的發(fā)展，可靠性設計優(yōu)化方法目前已經在工程中(尤其是航天裝備等具有高可靠性要求的領域中)被廣泛應用；可靠性設計優(yōu)化方法可以充分考慮復雜航天裝備的各類不確定性因素，如加工過程、材料特性、操作環(huán)境等，可以顯著提高關鍵核心航天裝備的壽命和可靠性，如可以提高衛(wèi)星姿控飛輪的壽命、導電滑環(huán)的可靠性、航天軸承和彈簧等關重件的壽命及復雜飛控系統(tǒng)的穩(wěn)定性等。在精度都滿足要求的情況下，在同等的計算條件下，可靠性設計優(yōu)化方法是具有更高優(yōu)化效率的方法，能夠減少設計優(yōu)化所需的時間。尤其對于某些特別復雜的航空航天裝備而言，高效率的方法能夠節(jié)約的時間是很可觀的。

典型的可靠性設計的優(yōu)化模型如下所示：

find:d,μX

min:f(d,μX,μP)

s.t.prob(gi(d,X,P)≥0)≥Ri,i=1,2,…,n

(1)

其中，f()是目標函數，prob()是當前設計點滿足第i個概率約束gi()的概率，n是概率約束的個數，d是確定性設計變量，X是隨機設計變量，μX是X的均值，P是隨機參數，μP是P的均值，Ri表示滿足第i個約束的期望概率，上標“Lower”和“Upper” 表示上、下邊界。

目前，可靠性設計優(yōu)化的主要研究方向包括可靠性分析和解耦方法兩個方向。可靠性分析方法包括解析法、降維法和模擬法。解析法是基于梯度的方法，包括極值分析法、矩法[1]和基于最大可能失效點(Most Probable Point, MPP)的方法[2]。尋找最大可能失效點的方法是較為有效的，也較為常用，如一次二階矩法[3]和二次二階矩法[4]。一次二階矩法包括可靠度指標法(Reliability Index Approach, RIA)[5]和性能測度法(Performance Measure Approach, PMA)[6]。一些學者提出了其他有效的可靠性分析方法，如先進均值法[7]、混合均值法[8]、圓弧搜索法[9]、增強混合均值法[10]和概率與凸集混合可靠性分析方法[11]、精確分析法[12]。

模擬方法[13-17](如蒙特卡羅法[16])被廣泛用于獲取高精度的可靠性分析結果。蒙特卡羅法通過大量地抽取樣本，判斷每一個樣本是否發(fā)生失效，并統(tǒng)計失效事件發(fā)生的比率，從而達到精確模擬的效果[17]。

基于解耦策略的可靠性設計優(yōu)化方法，主要可分為三類：雙循環(huán)法、單循環(huán)法、解耦法。雙循環(huán)法包含兩個嵌套的循環(huán)，其中設計優(yōu)化循環(huán)不斷地調用內部可靠性分析循環(huán)；單循環(huán)法通過某種途徑將內部循環(huán)進行了消除，如單循環(huán)單變量法[18]、單循環(huán)法[19]，及可信設計空間法[20]。

解耦法將設計優(yōu)化循環(huán)與可靠性分析循環(huán)順序求解，如序列優(yōu)化與可靠性分析法(Sequential Optimization and Reliability Assessment Method, SORA)[21]、直接解耦法[22]、序列逼近規(guī)劃法(Sequential Approximation Programming, SAP)[23]、凸線性逼近法[24]、罰函數法[25]、自適應解耦法[26]、最優(yōu)偏移向量法[27]、混合不確定優(yōu)化法[28]、區(qū)間不確定優(yōu)化法[29]、非概率魯棒優(yōu)化法[30]、概率可行域法[31]及多設計點方法[32]。

可靠性設計優(yōu)化解析方法的關鍵在于最大可能失效點MPP的尋找，而MPP點通常位于一個球面上。如果可靠性分析在球坐標中進行，那么在可靠性分析模型中，約束為一個球面，可以將其消除。本文提出一種在球坐標中求解可靠性設計優(yōu)化問題的方法，該方法可以將優(yōu)化循環(huán)與可靠性分析循環(huán)同時進行求解。

本文將首先在第1節(jié)中回顧RIA和PMA方法，在第2節(jié)中介紹球空間法，在第3節(jié)中通過對比算例驗證球空間法的有效性，并在第4節(jié)中給出結論。

1 可靠性設計優(yōu)化常用的方法

本節(jié)將主要回顧可靠度指標法RIA和性能測度法PMA，這兩種可靠性分析方法在雙循環(huán)方法中最為常用。在可靠性分析過程中，通常需要將相關的、非正態(tài)分布的變量X和P轉換為獨立的、正態(tài)分布的變量U(U～(0,1))。一些方法可以實現這種轉換:u=T(x,p), or (x,p)=T-1(u)，如Rosenblatt 轉換[33]和Nataf 轉換[34]。

1.1 可靠性指標法(RIA)

在可靠性指標法中, 目標函數是當前設計點的可靠度指標；約束函數是概率約束不大于期望值(假設當Gi(u)≤0時是可行設計)。RIA的數學模型如下：

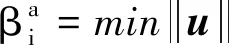
(2)

其中，u是標準設計空間中的隨機變量，它是(X,P)由原設計空間轉換而來的；Gi(u)是概率約束函數，對應于原設計空間的gi(d,X,P)函數。

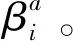
1.2 性能測度法(PMA)

性能測度法也被稱為逆可靠性分析法。在標準正態(tài)空間中，它將概率約束函數作為目標函數，將期望的可靠度指標作為約束，它的數學模型如下：

(3)

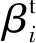
PMA方法在期望的可靠度指標球面上尋找逆最大可能失效點(Inverse Most Probable Point：IMPP)，該點具有最大的概率約束函數值(假設Gi(u)≤0時為可行域)。在通常情況下，PMA方法較RIA方法更加穩(wěn)定，因為它的搜索區(qū)域在一個球面或者超球面上。

2 球空間法

逆可靠性分析方法將概率約束函數作為目標函數，將可靠度指標作為約束函數，搜索空間為一個球面Gi(u)≤0，它的模型可以表示為：

find:u

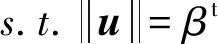
(4)

其中，βt是期望得到的可靠度指標，對應于式(1)中的期望獲得的可靠度概率R。

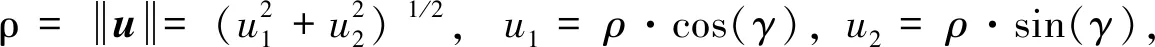
find:γ
min:G(u(ρ,γ))

(5)

可以看出，模型(5)變成了一個無約束的優(yōu)化問題，相對于帶約束的模型(4)，它更容易求解。本文提出的球空間法是將可靠性分析模型轉換為球坐標來表示，同時可以將可靠性分析循環(huán)與設計優(yōu)化循環(huán)并行求解。坐標轉換之后，約束函數g(x)變?yōu)間(x(ρ,γ))=g(ρ,γ)，其中x=(x1,x2,…,xn)，(ρ,γ)=(ρ,γ1,γ2,…,γn-1)。

2.1 利用球空間進行可靠性分析

find:γ
min:Gi(u(ρ,γ))
γ1∈(-π,π];γ2,…，γn-1∈(-π/2,π/2]

(6)

其中，u=(u1,u2,…,un)是迪卡爾坐標系下的隨機變量，(ρ,γ)=(ρ,γ1,γ2,…,γn-1)是球空間中的對應的隨機變量。

(7)

2.2 球空間模型

可靠性設計優(yōu)化的雙循環(huán)方法可以表示為式(8)和式(9)。

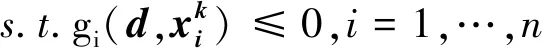
(8)

(9)

在上述模型中，設計優(yōu)化循環(huán)(式(8))和可靠性分析循環(huán)(式(9))是嵌套關系，無法將兩個循環(huán)表達為一個優(yōu)化循環(huán)。

本文將可靠性分析轉換為球坐標，從而可以通過極值條件(式(7))對可靠性分析循環(huán)進行簡化，進而將雙循環(huán)表示為一個優(yōu)化循環(huán)，即如式(10)所示

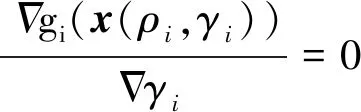
(10)

其中，(ρi,γi)是第i個概率約束在球空間中的IMPP點。

新模型(10)是一個常規(guī)的約束優(yōu)化模型，而且在推導過程中沒有近似求解，式(9)中的可靠性分析模型通過極值條件(式(7))進行代替，逆最大可能失效點x(ρi,γi)將通過迭代求解獲得。

2.3 球空間法的步驟與流程圖

球空間法的步驟與流程圖如圖1所示，步驟如下所示：

圖1 球空間法的流程圖Fig.1 Flow chart of sphere design space method

(3)建立可靠性設計優(yōu)化模型，如式(10)，設計變量(d,μX)及角度變量γi都將作為新的設計變量，IMPP點表示為x(ρ,γi)；

(4)對式(10)中的約束優(yōu)化問題進行數值迭代求解，直至設計變量滿足收斂條件。

3 應用

在本節(jié)中，通過2個算例來驗證球空間方法的有效性，對比方法包括雙循環(huán)法RIA、PMA+、SAP和SORA。計算結果通過蒙特卡羅方法進行驗證，樣本數量為107。

3.1 數值算例1

該算例為一個非線性數學問題[25]，包含兩個隨機設計變量X1、X2，三個概率約束g1、g2、g3。目標函數為兩個變量之和，模型如下

(11)

優(yōu)化結果如表1所示，可以看出解耦法SORA較雙循環(huán)法RIA和PMA+效率更高，SAP法具有更高的效率。函數調用次數表示了計算的效率，本文提出的球空間法對于目標函數和約束函數的調用次數均明顯減少，具有較高的計算效率。

在比較的5種方法中，所有方法的目標函數值和設計變量值都非常接近。因此，所有算法的求解精度都處于同一水平。表2給出了采用蒙特卡羅法對可靠性進行模擬求解的結果，βi表示第i個概率約束的可靠度指標。所有方法的可靠度指標值都較為接近，這從另外一個角度驗證了球空間法與其他方法在精度上處于同一水平。

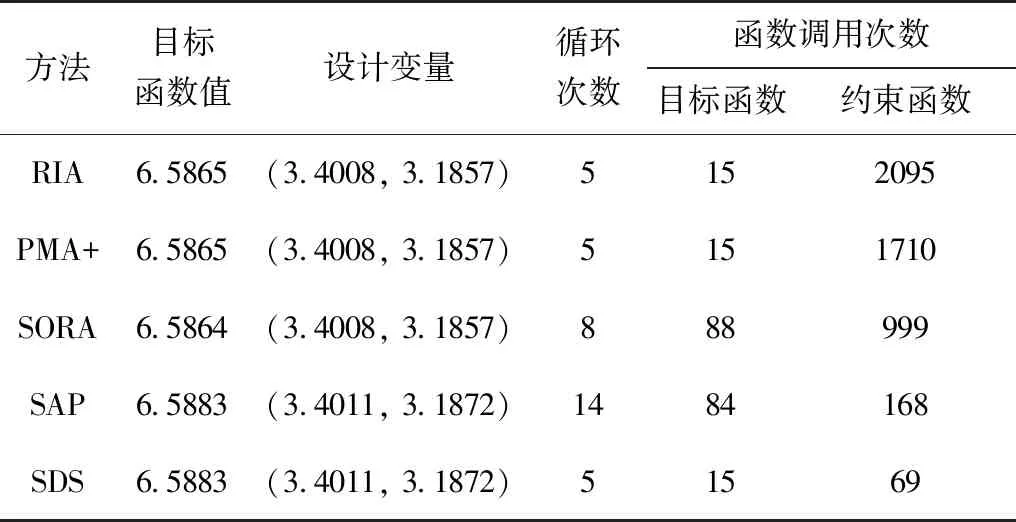
表1 算例1的優(yōu)化結果

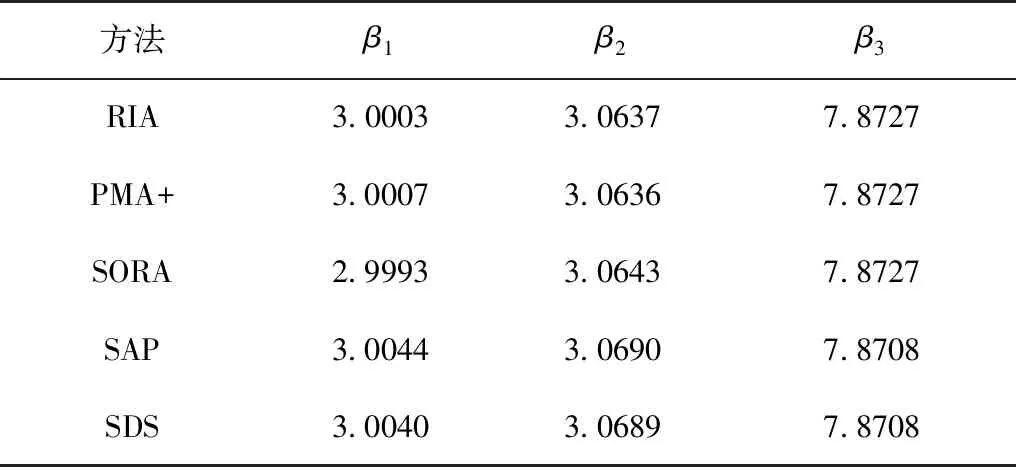
表2 算例1的蒙特卡羅可靠度指標

3.2 數值算例2

該算例[23]有兩個確定性設計變量d=[b，h]T，三個隨機參數X=[M，F，Y]T，數學模型如下

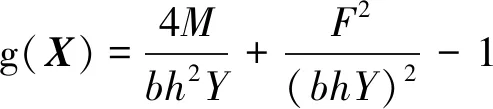
(12)

表3給出了優(yōu)化結果，所有方法的可靠度指標β1均在2.49附近，目標函數值和設計變量值都幾乎相等。因此，所有方法均具有相同的計算精度。在函數調用次數方面，本文提出的球空間法僅需要調用19次目標函數、34次約束函數，遠遠小于其他方法，因此本文提出球空間法具有更高的求解效率。

表3 算例2的優(yōu)化結果

4 結 論

本文提出了一種可靠性設計優(yōu)化的球空間法，該方法采用球坐標，可以方便地表示逆可靠性分析模型，并將其轉化為無約束優(yōu)化模型，從而可以利用極值條件將內層可靠性分析循環(huán)消除，將總的雙循環(huán)模型變?yōu)閱窝h(huán)模型。在新的模型中，設計優(yōu)化和可靠性分析可以同步進行。

通過算例進行的驗證表明，球空間法在計算精度上與其他方法處于同一水平，在求解效率上有明顯提升，因此本文提出的球空間法可以作為一種高效的可靠性設計優(yōu)化新方法。

本文所提出的方法對于復雜裝備的可靠性設計優(yōu)化，如復雜航天飛控裝備的可靠性設計，具有顯著效果。它將大大縮短可靠性設計的時間，降低整個產品的設計周期，同時保證航天產品的可靠性水平滿足設計要求。