非線性動力學系統的精細逐塊積分求解方法*

陳軍委

(1. 上海航天控制技術研究所·上海·201109；2.上海市空間智能控制技術重點實驗室·上海·201109)

0 引 言

對實際動力學系統特性的分析要求有效的數值仿真求解算法，尤其要求在采用大步長時仍然具有高精度的算法[1]。對于不存在或可以忽略高頻的結構動力學問題，普遍使用隱式積分方法(如Newmark、Wilson θ和Houbolt方法等)[2]或顯式方法(如Runge-Kutta法)進行瞬態分析和求解。通常，這些方法對于線性系統是準確和穩定的。例如，Newmark積分對于線性問題具有二階精度，并且無條件穩定。然而，當將上述方法應用于非線性動力學系統時，為獲得精確和穩定的數值解，選取的步長與系統最小周期、外部激勵周期和系統非線性項的變化周期相比，必須足夠小。因此，這些方法對于非線性動力學系統的求解效率不高，甚至容易失效[3]。

為此，研究者開發了面向非線性動力學系統的眾多數值方法，比如引入數值阻尼[4]，通過Lagrange乘子強制能量守恒[5]，以及采用算術能量守恒[6-7]等方法。Bathe等人提出了一種復合隱式積分算法，用于處理非線性問題[8-9]和線性剛性問題[10]。與上述富有成效的工作不同，本文作者采用了基于積分方程的方法。通常，積分格式會更具優勢。理論上講，積分算子比微分算子更容易實現處理，采用積分格式能更輕易推斷出解的特性。事實上，積分格式還可以在某些情形下縮減對象的維度[11]。

具體地，采用精細積分方法(precise integration method，PIM)[12]，指數矩陣的計算可以達到計算機的精度。Zhong、Williams和Lin等人指出，基于不可分割步長，精細積分可以獲得無條件的穩定性[12-14]。而Wang等人認為，雖然在考慮子步長的高階項截斷時，精細積分是條件穩定的，但大多數離散模型可以輕易滿足這種穩定條件[15]。此外，一階對角Pade近似對于精細積分也是無條件穩定的[16]，因此，精細積分由于具備高精度和穩定性，可被應用于處理非線性動力學問題。

在執行精細積分時，不可避免地需要計算關于非線性項和外部激勵的Duhamel積分。Zhong[13]和Lin等人[14]給出了外部激勵為線性、多項式、正弦和指數方程等形式或其組合形式時的積分精確計算公式。然而，這些計算公式并不適用于系統系數矩陣奇異或接近奇異的情況。Gu等人[17]基于多維展開的方法提出了一種修正的精細積分方法，來避免矩陣求逆。由此，原有的非齊次方程將轉化為齊次方程，但同時計算量也極大地增加了。Wang等人[15]通過顯式Gauss求積處理了Duhamel積分，但其準確性極大程度地依賴于Gauss求積的點數。Li等人[18]在每一個步長內使用了Lagrange三次插值近似非線性項，但仍然需要執行指數矩陣的求逆操作。

本文基于精細積分方法，針對非線性動力學系統，提出了精細逐塊積分方法(precise block-by-block integration method，PBIM)。此方法高度精確，在使用大步長時也可保持穩定，無須矩陣求逆便可以處理非線性項。本文余下內容依次為：在第二部分，描述了精細逐塊積分方法，以及其精度和穩定性分析；在第三部分，列舉了三個數值算例以驗證本方法的有效性；最后，在第四部分給出了有關結論。

1 精細逐塊積分方法

1.1 方法描述

具有時變剛度的二階動力系統通常以矩陣形式表示為

(1)

不失一般性，K(t)可以劃分為定常部分和時變部分，即K(t)=K1+K2(t)。式(1)由此可以變換為如下的一階形式

(2)

其中，Ip和0p分別是p×p階單位陣和零矩陣。

式(2)可以改寫為

(3)

其中，

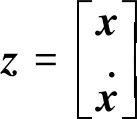
令n=2p。顯然，A是n×n階常矩陣，g(t,z)是關于時間、狀態向量和外部激勵的n維向量方程。需要指出的是，式(3)是相比于式(1)更為通用的形式，雖然前者由后者推導而來。下文將以式(3)為對象進行討論。

將式(3)進行積分，得到第二類非線性Volterra積分方程，即

(4)

由于式(3)源于實際動力系統，所以認為其積分核滿足Lipschitz條件，即系統存在唯一解[11]。以步長h為離散時間間隔，記離散時間點的狀態為zi(i=0,1,2,…)，即zi=z(ti)。定義時間間隔[t2m,t2m+2](m=0,1,2,…)為一間隔塊，則在每一間隔塊內，得

(5)

(6)

對式(5)～(6)應用Simpson法則，得

(7)

(8)

由此，Duhamel積分可由精細積分求取[12]。在整個計算流程中，指數矩陣只需被計算一次。以eAh為例，應用指數函數的附加定理，即2N算法，得

eAh=T2N

(9)

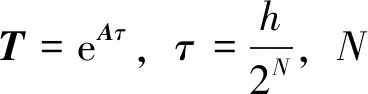
(10)

其中

(11)

τ非常小，故將前4項或前5項展開，便可獲得足夠高的精度。為避免出現運算圓整誤差，可將不變部分I和增量部分Ta分別進行存儲。將eAh進行分解，代入式(10)，可得

T2N>=>(T2)2N-1=(I+2Ta+Ta·Ta)2N-1

(12)

最終，經N次形如Ta?2Ta+Ta·Ta的遞歸，eAh的數值結果逼近了計算機的運算精度。

需要指出的是，式(7)～(8)要同時求解未知量z2m+1和z2m+2。在此，可以應用任何代數方程求解算法。例如，可以使用Newton迭代下山法以避免矩陣求逆，或采用同倫連續方法以實現全局收斂的效果[20]。

1.2 穩定性

積分方法的數值穩定性條件是指，對于單自由度系統，其迭代放大矩陣的譜半徑小于或等于1[21]。為考察精細逐塊積分方法的數值穩定性，需考慮如下的線性齊次算例

(13)

其中，ω>0,ξ≥0。

采用Zhong和Williams提出的變換[12]，式(13)可寫為

(14)

其中，

應用式(7)～(8)，可得

(15)

相應的放大矩陣為

D=eAh

(16)

顯然，放大矩陣D的特征值λ滿足

|λI-eAh|=0

(17)

在不考慮Taylor展開截斷誤差時，求得特征值為

(18)

顯然，對于ξ≥0，特征值λ常滿足|λ|≤1。當考慮Taylor展開截斷誤差時，如文獻[15, 22]所指，子步長τ趨近集中。Wang[15]指出，在這種情形下，截斷階數q=4、5和二分階數N=20對于大多數結構而言均可保證穩定性，只有在選取相對系統無阻尼固有周期的大子步長時，才會出現不穩定的結果。

1.3 精度

簡便起見，考慮形如g(t,z(t))=G(t)z(t)的線性案例。對于初值問題，定常系統的精細積分數值解接近計算機的精度[13]。因此，精細逐塊積分的誤差滿足

(19)

(20)

其中

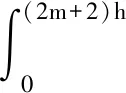
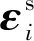
為進一步驗證以上結論，考慮如下的單自由度線性系統

(21)

其中，ω=1.0，ξ=0.05，其解析解為

x=e-ξt(c1cosηt+c2sinηt)+s1cosπt+s2sinπt

(22)

其中，

表1對比了精細逐塊積分方法、精細積分方法[12]的數值解和系統的解析解。當步長為0.01s時，相比于解析解，精細逐塊積分方法可以精確至6位有效數字，高于精細積分方法。表2列出了精細逐塊積分方法在不同步長下的誤差。可以看出，當步長減半時，誤差約縮減為1/16，這與上述收斂階數的結論非常吻合。

表1 單自由度系統的數值解(0s至1s)

表2 不同步長下精細逐塊積分方法的誤差

2 數值算例

為驗證精細逐塊積分方法的有效性，本部分給出了3個算例。

2.1 算例I

考慮兩自由度Fermi-Pasta-Ulam問題[23]。如圖1所示，系統包含一剛性線性彈簧和兩個非線性軟彈簧。本系統存在高頻振蕩，其Hamilton函數為

(23)

其中，qi和pi(i=1,2)分別為廣義坐標和廣義動量矩。相應的Hamilton正則方程為

(24)

圖1 兩自由度Fermi-Pasta-Ulam問題Fig.1 The 2-DOF Fermi-Pasta-Ulam problem

令ω=50，用精細逐塊積分方法求解式(24)。設置絕對誤差和相對誤差均為10-14，將Matlab求解器ode15s的求解結果作為參考解。表3列出了經精細逐塊積分方法、四階Runge-Kutta法(RK4)和Newmark方法解出的q1值。可以看出，精細逐塊積分方法在步長設置為0.001s時具有9或10位有效數字的精度；當步長增大為0.005s時，精細逐塊積分方法仍然具有7位有效數字的精度。然而，在設置步長為0.001s時，RK4方法只有6位有效數字的精度；Newmark 方法直到步長小至0.0001s時才有所收斂，并且只有1或2位有效數字的精度。

表3 經ode15s、精細逐塊積分方法、RK4法和Newmark方法求得的q1值

圖2繪出了上述3種方法從0至80s的時間歷程響應。精細逐塊積分方法和RK4法的步長為0.01s，Newmark方法的步長為0.0001s。顯然，Newmark方法在步長小至0.0001s時仍然不穩定，而精細逐塊積分方法和RK4法可以獲得穩定解。然而，如表3所示，雖然RK4法看起來長時穩定，但不如精細逐塊積分方法精確。

2.2 算例II

考慮變系數非線性周期系統[24]

(25)

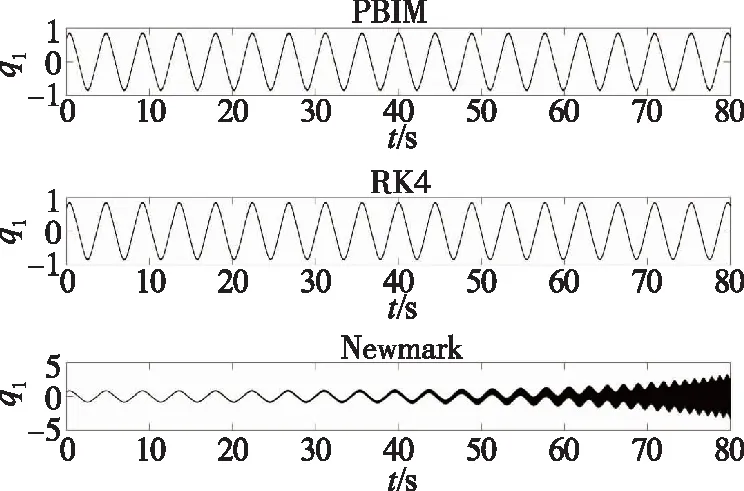
圖2 經精細逐塊積分方法、RK4法和 Newmark方法求解的q1響應Fig.2 Responses of q1 by the PBIM, the RK4 method and the Newmark method

其Galerkin解為

(26)

其精度可達10-5，可認為是參考解。分別應用精細逐塊積分方法、RK4法和Newmark方法求解式(25)，將相應的x1數值解的誤差繪制在圖3至圖5中。在圖3中，對精細逐塊積分方法依次選取步長h=0.1s和h=0.01s。顯然，即使步長增大了10倍，相應的誤差仍保持在10-5。圖4展現了步長依次設置為h=0.1s和h=0.01s時，由RK4法獲得的x1的誤差。與精細逐塊積分方法不同，當步長增大10倍時，誤差也自10-2至10-1放大了10倍。Newmark方法的表現最差。如圖5所示，Newmark方法要求非常小的步長，直到步長h=0.0001s才可保持數值穩定。

圖3 不同步長下精細逐塊積分方法的x1的誤差Fig.3 Errors of x1 by the PBIM using different step sizes

圖4 不同步長下RK4法的x1的誤差Fig.4 Errors of x1 by the RK4 method using different step sizes

圖5 不同步長下Newmark方法的x1的誤差Fig.5 Errors of x1 by the Newmark method using different step sizes

2.3 算例III

最后，考慮如下的非線性剛性問題

(27)

圖6 精細逐塊積分方法和ode15s求解誤差比較(h=0.001s)Fig.6 Comparison of the errors by the PBIM and ode15s(h=0.001s)

3 結 論

本文提出了精細逐塊積分方法。作為隱式積分格式，此方法可以輕易滿足穩定性條件，達到4階精度。因此，與Newmark方法和RK4法相比，對非線性動力系統應用精細逐塊積分方法，可以在大步長的條件下獲得高精度和穩定的數值解。此外，由于本方法不需要進行矩陣取逆運算，因此對具有奇異或接近奇異的系統矩陣的問題仍然有效。

附錄

定理A.1[11]令序列ξ0,ξ1,…滿足

其中，

得