李群變分積分子在最優航跡規劃中的應用*

楊盛慶，王 禹，陳 樺，王嘉軼，劉美師

(1. 上海航天控制技術研究所·上海·201109； 2. 上海市空間智能控制技術重點實驗室·上海·201109)

0 引 言

飛行器個體的航跡優化可分為離線算法和在線算法兩類。離線的航跡優化算法著眼于全局最優的可行路徑(算法的數值結果多為可行航跡點的序列)，可以脫離個體的力學模型；在線的航跡優化算法傾向于采用反饋控制和局部的最優控制，與個體的力學模型密不可分。個體航跡優化的離線算法種類繁多。快速隨機生成樹(Rapidly Exploring Random Tree, RRT)以隨機的數據結構為基礎，其算法具有高效、收斂的特性。本文選取RRT來規劃空間中的可行航跡點序列，并將所得的航跡點用作局部最優控制的邊界條件，從而實現了離線算法與在線算法的結合，得到了飛行器個體在區域內的航跡優化結果。

飛行器系統的力學模型是研究其最優控制的基礎，分析其力學特性，特別是其拉格朗日函數和運動方程，具有重要的研究意義。對于六自由度(6DOF)的飛行器模型，其位形變量可分為位移變量和姿態變量兩類。與分析力學著眼于力學系統的運動方程有所不同，幾何力學強調力學系統自身的幾何特性(不變量及其守恒律)[1-2]。在描述空間中具有對稱性的個體的運動方程時，可以借助流形的工具來刻畫變量在運動過程中所需滿足的性質。譬如，剛體在空間中的姿態變量屬于李群，基于李群概念構建的運動方程可以時刻確保姿態變量屬于李群，進而提高計算的精度[3]。李群變分積分子是對剛體進行數值積分的一種數值格式[4-6]，Marsden、Junge和Ober將其用于構造離散位形空間中的離散力學與最優控制問題(Discrete Mechanics and Optimal Control, DMOC)[7]，將原本的連續空間中的最優控制問題轉化為離散空間中的一個最優化問題，并實現了個體之間不存在相互作用的質點編隊的最優控制[8-9]。Lee、Leok和McClamroch等基于DMOC原理，研究了由李群變分積分子構造的剛體最優控制問題，并將其成功應用于衛星編隊等領域[10-12]。近期，國外學者將變分積分子領域的研究拓展到了衛星軌道積分[13]和受力拉格朗日動力學系統[14]。這些研究成果為自主智能的無人系統發展[15-16]打下了良好的數學理論基礎。

結合基于隨機算法的航跡點規劃和基于幾何力學的最優控制，實現了飛行器個體在區域內的航跡優化。首先介紹了DMOC的基本理論，推導得到了剛體的李群變分積分子，然后基于李群變分積分子給出了剛體最優控制的數值求解格式。最后，結合全局的RRT算法和局部的最優控制(DMOC)，實現了全局環境中飛行器個體的航跡優化。

1 變分原理與剛體運動方程

1.1 拉格朗日動力學系統與變分原理

定義1：位形空間Q上的Lagrange力學系統，其拉格朗日函數Lagrangian的定義為L:TQ→R，滿足Euler-Lagrange方程

(1)

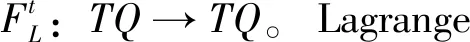
定義2：設Φ是群G在流形Q上的作用，將Φ對于辛流形T*Q的右作用提升Φ*定義為

(2)

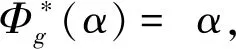
左作用下Φ不變。

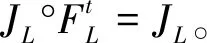
Noether定理可以理解為，當系統滿足左(右)提升不變的條件時(譬如自由系統的平移運動和旋轉運動)，其Lagrange流(運動狀態)將保持不變。將上述概念拓展到離散Lagrange力學系統，即可得到變分積分子的數值特性。

1.2 剛體運動的變量空間

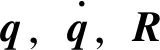
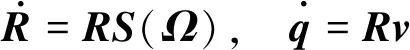
(3)

角速度Ω是體坐標系下的一類變量，用以描述運動中姿態角的變化率。基于角速度Ω，可以定義角速度矩陣S(Ω)，且S(Ω)滿足

(4)

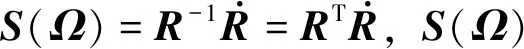
1.3 李群與李代數

李群是具有旋轉不變性的群，可以描述具有對稱性的運動物體。例如，空間中固定質心的剛體可由SO(3)刻畫其姿態，其運動狀態則可由李代數SO(3)中的元素表述。SO(3)是一類經典的李群。

李群G是一個Banach空間，具有零元和單位元。其群結構與其流形結構在如下意義下相容

μ:G×G→G,(g,h)|→gh

(5)

李代數是李群在零元鄰域內的局部線性化，用以刻畫李群的局部信息，從而表述其運動狀態。

定義3：指數映射EXP:g→G，滿足

EXP(X)=eεX∈G

(6)

命題1：對于任意S(Ω)，存在η∈SO(3)，滿足δR=Rη。

證明：根據指數映射的定義，對于任意R∈G，存在η∈g，滿足R=Reεη(ε→0)。對指數函數進行Talyor展開，滿足

(7)

由變分定義可得

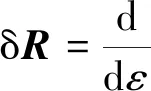
(8)

將式(7)代入式(8)，計算可得

δR=Rη

(9)

同理，δq=Rξ。

1.4 剛體運動方程

對剛體的Lagrangian作變分處理，可以得到剛體運動的Euler-Lagrange方程。考慮三軸向對稱的剛體，其轉動慣量矩陣為一個對角矩陣，不妨令J=diag{J1,J2,J3}。引入非標準轉動慣量矩陣Jd，滿足

J=tr(Jd)I3×3-Jd
Jd=tr(J)I3×3-J

(10)

在剛體的動能函數中，關于角速度的部分可以改寫為

ΩTJΩ=Ω1J1Ω1+Ω2J2Ω2+Ω3J3Ω3
=tr(S(Ω)JdS(Ω)T)

(11)

記m為個體質量，慣性矩陣M=diag{m,m,m}；重力方向矢量k=(0,0,1)T。剛體的Lagrangian可以定義為

L(Ω,v,R,q)=E(Ω,v)-V(R,q)

(12)

Lagrangian的變分滿足

(13)

(14)

記控制扭矩τ1∈SO(3)*和控制力τ2∈(3)*。由Lagrange-d-Alembert原理可得剛體運動方程為

(15)

2 李群變分積分子及其數值特性

2.1 離散變分原理

在連續空間中，可以定義位形空間、Lagrangain函數和作用函數，通過變分原理得到Euler-Lagrange方程。同樣地，在離散變量空間中可以定義上述空間和函數的離散形式，得到離散的Euler-Lagrange方程,如圖1所示。

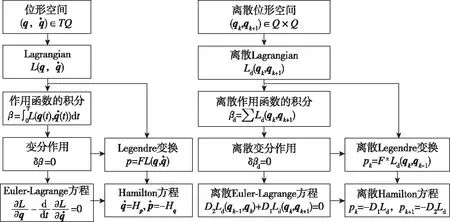
圖1 連續空間與離散空間的運動方程推導體系Fig.1 Euler-Lagrange equation induced in continuous and discrete variable spaces

2.2 變分積分子的數值特性

定義4：將Legendre變換定義為位形空間的切叢到余切叢的映射FL:TQ→T*Q，滿足

(16)

相應地，離散的Legendre變換可定義為

(17)

(18)

離散Legendre變換定義的變分積分子是一種數據積分格式，能夠保持動力學系統的能量特性。基于變分積分子的數值積分能夠長時間地保持系統能量，從而可得到更加符合實際的運動過程，如圖2所示。

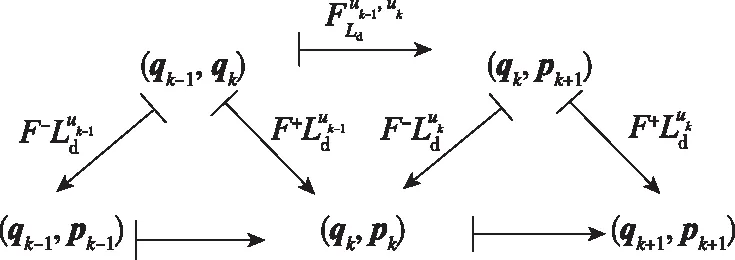
圖2 變分積分子的數值積分流程Fig.2 Numerical process of variational integrator

引理2[1]：(Noether定理離散形式)一個離散Lagrange系統，如果其離散Lagrangian函數在左(右)提升Φ:G×Q→Q的作用下不變，那么對應的離散Lagrange動量映射JLd:Q×Q→g*關于系統的離散Lagrange流FLd:Q×Q→Q×Q則是守恒的，即有JLd°FLd=JLd。

Noether定理的離散形式揭示了變分積分子的數值特性，即對于一個不受外力作用的動力學系統而言，變分積分子可以圍繞不變的離散Lagrange流而構造算法，實現可長時間保持精度的數值積分方法。

2.3 離散剛體運動方程

李群變分積分子是剛體的離散Lagrangian作離散變分而得到的數值積分格式。首先，給出離散變量的差分格式，記時間步長為h，選取向前差分格式

(19)

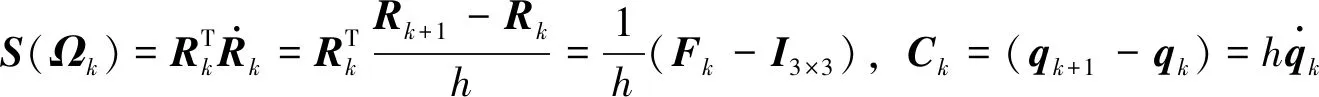
離散Lagrangian的定義為

Ld(Fk,Ck,Rk,qk)

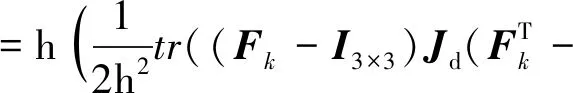
(20)

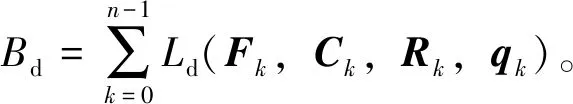
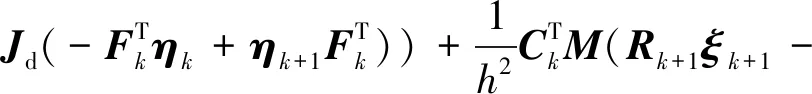
Rkξk)+mgkRkξk}

(21)

整理可得剛體的離散運動方程

(22)

2.4 李群變分積分子

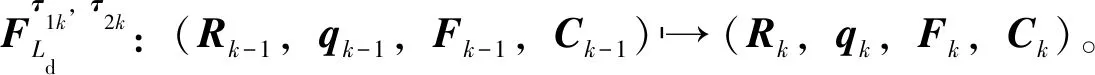
在數值計算的過程中，為了保證Fk∈SO(3)，需引入其近似的表達式

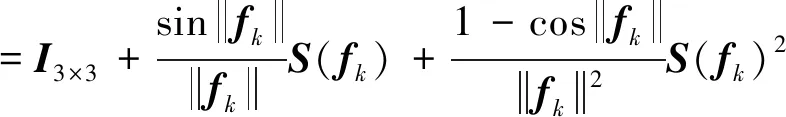
(23)

在數值計算的過程中，可利用公式(23)將離散運動方程中的Fk替換為與fk相關的項。只需求解滿足方程組的fk，即可得到相應的Fk。

3 離散力學與最優控制與飛行器航跡優化

3.1 離散力學與最優控制(DMOC)

DMOC屬于直接法，相較傳統的直接法，DMOC能夠更好地保持系統的守恒量。不同于傳統直接法中的離散運動方程，DMOC是在離散的Lagrangian的基礎上利用離散變分原理求得運動的離散方程，使得離散變量能保持其性質。在由此得到的離散運動方程和李群變分積分子的基礎上，求解與最優控制等價的最優化問題，規劃離散節點處的運動狀態和對應的控制量。控制力和控制力矩的工程約束主要體現于優化問題構造過程中的變量取值范圍的約束。將DMOC進行航跡規劃的具體形式如下

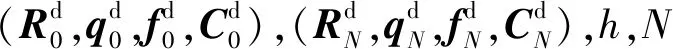
使得

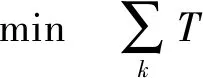
滿足

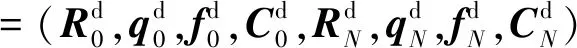
(24)

最優航跡的目標有多種，比如能耗最小或距離最短。針對耗能最小的規劃問題，其代價函數可表述為

(25)

代價函數T是關于控制力和控制力矩的正定函數。針對控制力和控制力矩的區別，根據經驗調整加權矩陣Wr,Wt，從而體現兩者實現代價的不同性。

對于路徑最短的最優控制問題，其代價函數可表述為

(26)

圖3(a)為不同代價函數的DMOC求解結果。對于能耗最小的最優控制問題，其個體的運動更依賴于慣性，進而需要以更長的路徑作為代價；對于路徑最短的最優控制問題，其更依賴于由外部控制實現航跡的改變，從而需要付出更多的能耗代價。圖3(b)為不同末態約束的最短路徑示意。一般而言，在最優化求解兩點邊值問題時，初態和末態的時間是給定的。對于末態時間不確定的時間最優問題，需要重新構造DMOC的目標函數和約束。

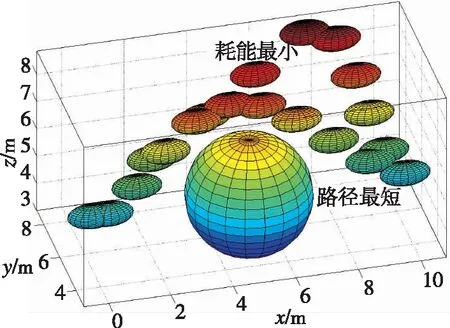
(a)不同代價函數的DMOC求解結果

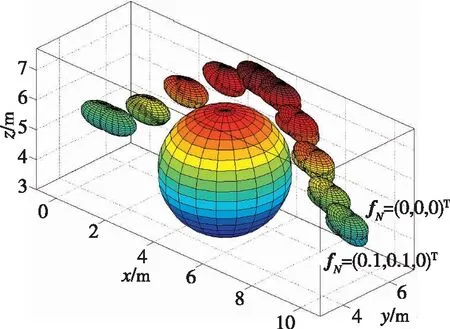
(b)不同末態約束的最短路徑示意圖3 不同代價函數的DMOC求解結果與 不同末態約束的最短路徑示意Fig.3 DMOC results for shortest routing and minimum energy with DMOC results for different final conditions

3.2 RRT的基本原理

RRT是一種高效的離線算法，可以得到給定障礙區域內的可行航跡點序列。算法的主體為一個循環過程，具有快速收斂到最優(次優)航跡點序列的性質[17-18]。RRT算法可分為如下四個部分。

(1)樹的延拓：在每次循環中，尋找一個可行的新航跡點。

(2)樹枝的優化，參見表1和圖4所示。

表1 RRT樹枝的優化

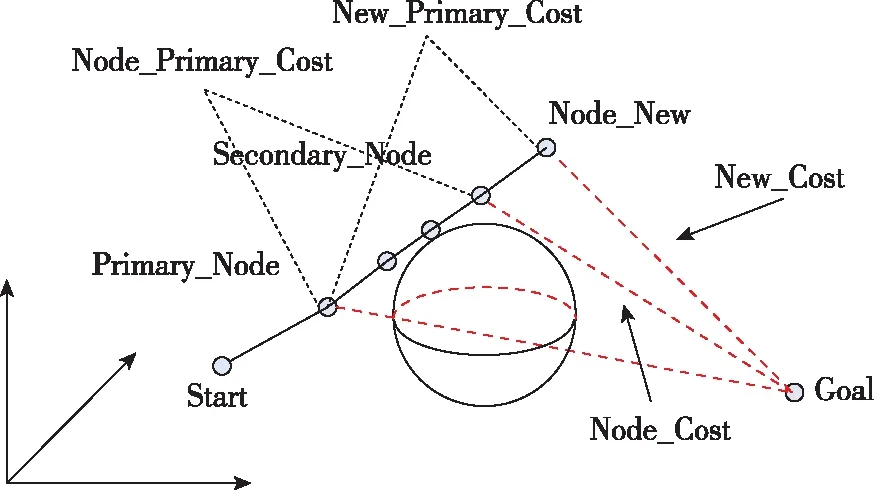
圖4 RRT樹枝優化算法的示意圖Fig.4 Illustrations of RRT branch optimizations

(3)樹結構的優化，參見表2和圖5所示。

表2 RRT樹結構的優化

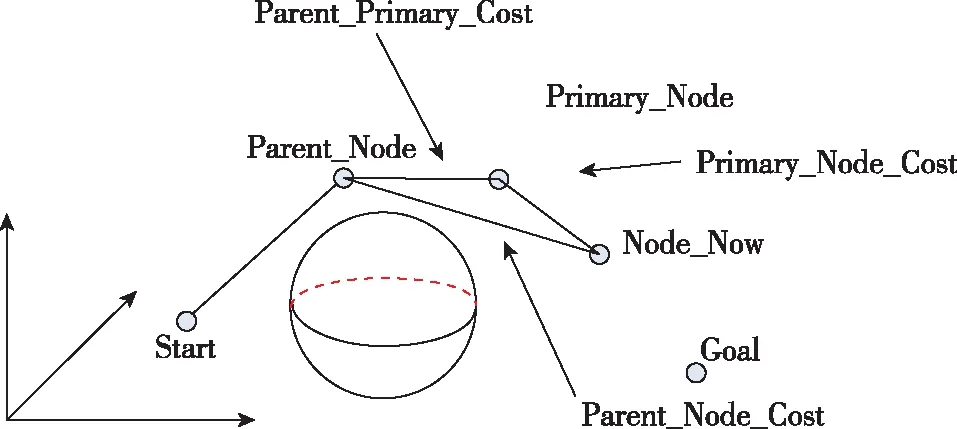
圖5 RRT樹結構優化算法的示意圖Fig.5 Illustrations of RRT structure optimizations

(4)尋找最優航跡：在所生成的樹的結構中找一條對應航跡最短的樹枝，樹枝上的航跡點即為最優航跡點序列。

3.3 基于RRT與DMOC結合的飛行器的航跡優化

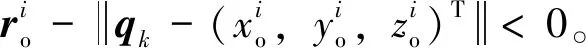
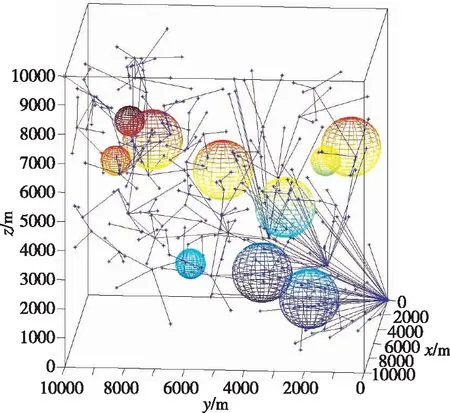
(a)左視圖

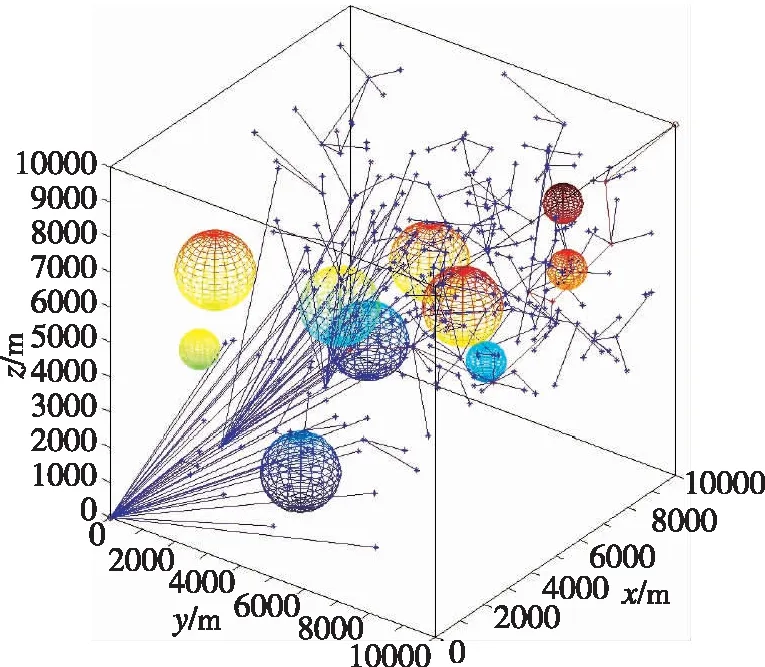
(b)右視圖圖6 三維歐式空間中RRT的規劃效果Fig.6 Illustrations of RRT optimizations in 3D Euclid space

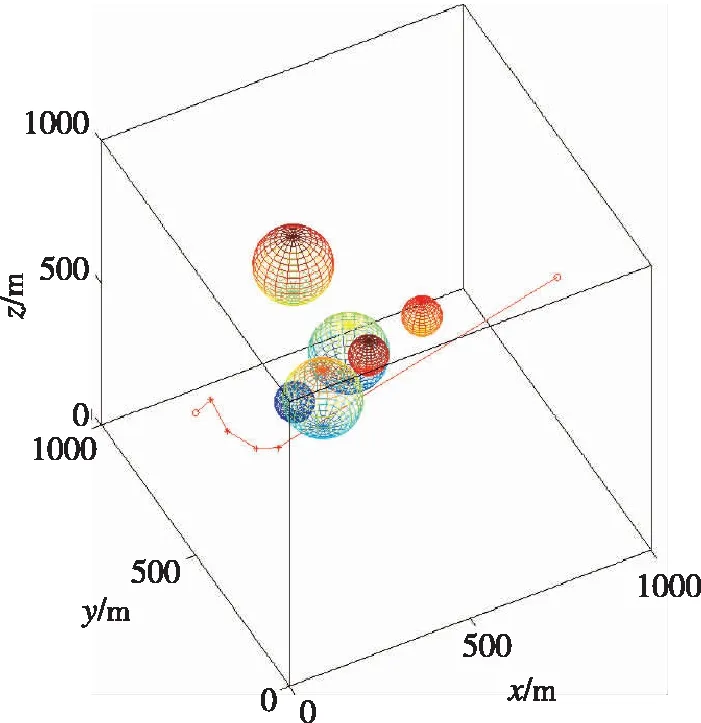
(a)障礙環境中的RRT規劃航跡點

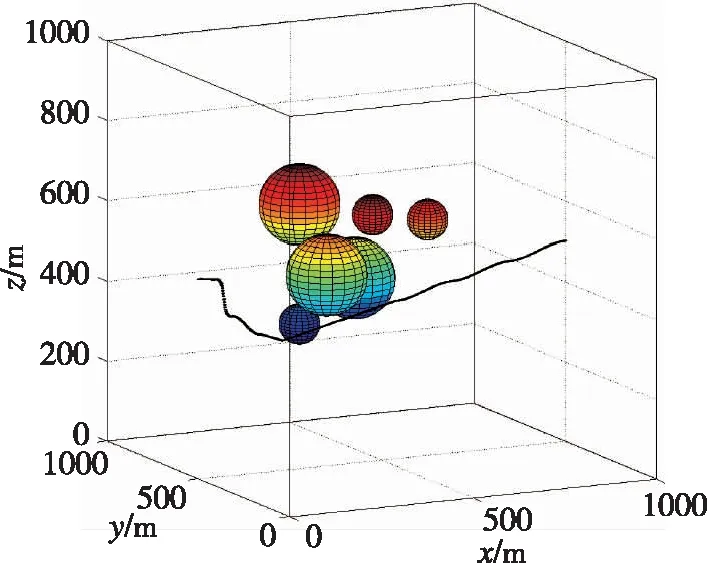
(b)DMOC實現的無人飛行器航跡優化的結果圖7 由RRT生成的障礙環境中的最優航跡點和 由DMOC規劃的最優航跡示意Fig.7 Trajectory points of RRT method in obstacles environ- ment and DMOC results of trajectory planning of UAV

4 結 論

航跡優化算法需要兼顧最優性和實時性，將不同層次的規劃算法進行結合是實現此項要求的一種選擇。由隨機離散算法(RRT)給出可行航跡點序列，繼而通過離散力學與最優控制(DMOC)實現相鄰航跡點之間的銜接。本文推導了在重力環境下，六自由度剛體的李群變分積分子形式，將其應用于相鄰航跡點之間最優控制的求解。此類方法亦能應用于衛星編隊的航跡優化，實現衛星小推力控制形式的過程最優控制。