《正弦定理》說課稿

李盼娟

(河南師范大學(xué)數(shù)學(xué)與信息科學(xué)學(xué)院，河南 新鄉(xiāng) 453000)

各位評委老師好，今天我說課的題目是《正弦定理》。《正弦定理》是必修五第一章第一節(jié)的內(nèi)容，我將以新課程標(biāo)準(zhǔn)的理念指導(dǎo)本節(jié)課的教學(xué)，從教材、教法、學(xué)法、教學(xué)過程和說課綜述五個方面來談?wù)勎覍滩牡睦斫夂徒虒W(xué)的設(shè)計，請各位專家、評委老師批評指正。

一、說教材

(一)教材的地位和作用

本節(jié)課《正弦定理》選自《普通高中課程標(biāo)準(zhǔn)實驗教科書數(shù)學(xué)·5》(必修)一書，是第一章“解三角形”的第一節(jié)內(nèi)容，本節(jié)內(nèi)容編排在學(xué)習(xí)了三角函數(shù)和三角恒等變換之后，這里我們多次用到正弦函數(shù)，進而通過本節(jié)課的學(xué)習(xí)既可以對正弦函數(shù)方面的知識加深理解，又可以為后面學(xué)習(xí)余弦定理打下基礎(chǔ)，因此，《正弦定理》是本章的重要內(nèi)容。它與我們?nèi)粘！⑸睢⑸a(chǎn)和科學(xué)研究都有著緊密的聯(lián)系，所以學(xué)習(xí)這部分內(nèi)容有著廣泛的現(xiàn)實意義。

(二)教學(xué)目標(biāo)

1.知識與技能目標(biāo)：學(xué)習(xí)正弦定理的定義，學(xué)會應(yīng)用正弦定理來解三角形；

2.過程與方法目標(biāo)：通過讓學(xué)生觀察，猜想，運用由特殊到一般的思想方法，注重正弦定理的推導(dǎo)證明過程，加深學(xué)生對定理的理解；

3.情感態(tài)度與價值觀目標(biāo)：在學(xué)習(xí)正弦定理的過程中，幫助學(xué)生養(yǎng)成勤于思考的習(xí)慣，在探究知識的過程中體會數(shù)學(xué)與生活的緊密聯(lián)系[2]。

(三)教學(xué)重點和難點

1.重點：通過探索三角形的邊角關(guān)系，發(fā)現(xiàn)并證明正弦定理，初步學(xué)會應(yīng)用正弦定理解三角形；

2.難點：用“作高法”證明正弦定理，讓學(xué)生掌握正弦定理的基本應(yīng)用[3]。

二、說教法

(一)教學(xué)手段

基于新課程標(biāo)準(zhǔn)的要求和本節(jié)課知識內(nèi)容的特點，為了使學(xué)生更好地理解并掌握正弦定理，在教學(xué)手段上采用板書、PPT和幾何畫板等多媒體相結(jié)合的方式，從問題情境創(chuàng)設(shè)入手，引導(dǎo)學(xué)生觀察發(fā)現(xiàn)，從直觀想象到發(fā)現(xiàn)猜想，再到抽象概括，最后得出結(jié)論，一步一步探索知識的生成過程，體會獲得知識成果的喜悅。

(二)教學(xué)方法及其理論依據(jù)

本節(jié)課采用的教學(xué)方法是“發(fā)現(xiàn)探究法”，讓同學(xué)們分組討論，主動探究，合作交流，從現(xiàn)實中實際例子出發(fā)，利用此年齡階段學(xué)生的好奇心和認(rèn)知特點，一開始就抓住學(xué)生眼球，然后引導(dǎo)學(xué)生發(fā)現(xiàn)三角形的邊角關(guān)系，師生進一步探究，以直角三角形為特例出發(fā)，將特殊到一般的數(shù)學(xué)思想滲透在教學(xué)過程中，從而得出正弦定理，并說明它在解三角形中的應(yīng)用。教學(xué)中努力做到鍛煉學(xué)生的思維，教會他們數(shù)學(xué)的思考方法，教師要真正做到“授之以漁”。

三、說學(xué)法

本節(jié)課的授課對象是高二年級的學(xué)生，經(jīng)過之前一年的數(shù)學(xué)學(xué)習(xí)，學(xué)生已經(jīng)學(xué)習(xí)過三角函數(shù)，有一定的知識儲備，況且這一階段學(xué)生對于前一段所學(xué)知識并沒有完全遺忘，根據(jù)人的遺忘規(guī)律，及時復(fù)習(xí)，并引入新課，探索新知，明確學(xué)習(xí)目的，抓住學(xué)生數(shù)學(xué)學(xué)習(xí)的心理特點，運用生動形象，形式多樣數(shù)學(xué)方法，深入淺出，讓數(shù)學(xué)課堂真正成為探究性課堂，提高課堂效率。接下來我將說明以下幾個方面的學(xué)法指導(dǎo)：

(一)培養(yǎng)學(xué)生通過觀察、發(fā)現(xiàn)、探究、檢驗等方法，學(xué)習(xí)正弦定理的相關(guān)知識，從實例出發(fā)，尋求解決方法，發(fā)現(xiàn)三角形邊角關(guān)系，進一步分析探究，歸納推理，推導(dǎo)出正弦定理，并加以證明，這正是一個分析和推理的全過程。

(二)學(xué)生獨立思考，在探索性實驗中以直角三角形為特例，并推廣到一般情況，親身經(jīng)歷定理證明的過程方法。如用“作高法”在直角三角形中進行證明完成后，分別又在“銳角三角形”和“鈍角三角形”中，通過直觀演示，計算推理，同樣得到了正弦定理，這樣，我們就可以把正弦定理推廣到任意三角形的情形中去。

四、說教學(xué)過程

(一)創(chuàng)設(shè)情境，提出問題

如圖1，河的兩岸有A,B兩點，要測量兩點之間的距離.測量者在A的同側(cè)，在所處的河岸邊，選定一點C，測出AC的距離是55m，∠BAC=51°，∠ACB=75°.求A,B兩點間的距離(精確到0.1m).

引導(dǎo)學(xué)生分清題意，在△ABC中，我們知道一條邊AC的長度，并知道兩個角∠BAC，∠ACB的大小，求其中一條邊AB的長，啟發(fā)學(xué)生用何種方法才能求解。

(二)提出問題，導(dǎo)入新知

我們知道，在任意三角形中有大邊對大角，小邊對小角的邊角關(guān)系，那么對于上面情境中的三角形，我們能否得這個邊、角關(guān)系準(zhǔn)確量化的表示呢？如果大家對任意三角形知如何下手，那么能否優(yōu)先考慮曾經(jīng)學(xué)過邊角關(guān)系的三角形，即直角三角形。

如圖2，在Rt△ABC中，∠C是最大的角，所對的斜邊c是最大的邊，要考慮邊長之間的數(shù)量關(guān)系，就涉及到了銳角三角函數(shù).根據(jù)正弦函數(shù)的定義，

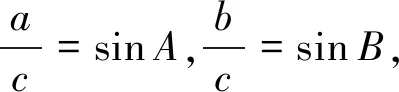
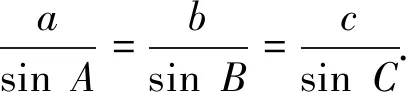
設(shè)計意圖：從已學(xué)過的直角三角形出發(fā)，因為我們之前學(xué)過勾股定理，深入探討邊角關(guān)系，得到正弦定理，此時學(xué)生會有疑問，這樣的等式是在直角三角形中推導(dǎo)出來的，那么在任意三角形(銳角三角形，鈍角三角形)中仍然成立嗎？接下來分小組討論，我們繼續(xù)深入探討[1]。

(三)深入探究，得出結(jié)論

1.如圖3，當(dāng)△ABC是銳角三角形時，設(shè)邊AB上的高是CD，根據(jù)三角函數(shù)的定義，

解：因為CD=asinB，CD=bsinA，所以asinB=sinA，

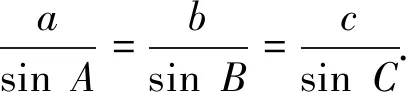
設(shè)計意圖：由以上討論，在銳角三角形中想

到“作高法”構(gòu)造直角三角形，化未知為已知，進行學(xué)習(xí)遷移，進一步討論。

2.如圖4，當(dāng)△ABC是鈍角三角形時，過點C作AB邊上的高，交AB延長線于點D，根據(jù)銳角三角函數(shù)的定義，

解：有CD=asin∠CBD=asin∠ABC，CD=bsinA.

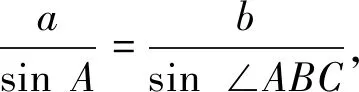
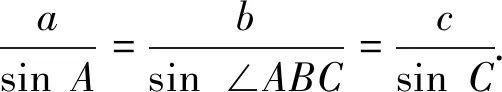
設(shè)計意圖：同銳角三角形討論方法類似，在這里我們?nèi)匀灰龑?dǎo)學(xué)生構(gòu)造直角三角形，利用同一條邊長的不同表示，發(fā)現(xiàn)并得出正弦定理。

3.得出結(jié)論

正弦定理：在一個三角形中，每條邊和它所對的角的正弦比是相等的，即

一般地，三角形中三個角A,B,C與它們的對邊a,b,c叫做三角形的元素。如果已知三角形的幾個元素來求其他元素的過程就叫做解三角形[1]。

(四)例題講解，課堂練習(xí)

1.例題講解

例1.在△ABC中，已知A=32.0°,B=81.8°,a=42.9cm,解三角形.

例2.在△ABC中，已知a=20cm,b=28cm,A=40°,解三角形(角度精確到1°，邊長精確到1cm).

設(shè)計意圖：在例1中已知兩角及一邊，解三角形即可求出另外兩條邊和一角；在例2中已知兩邊及一角，此時利用正弦定理解三角形時，要特別注意會出現(xiàn)解不確定的情況，一般可根據(jù)三角形中“大邊對大角和三角形內(nèi)角和定理”來取舍。

2.課堂練習(xí)

練習(xí)1.在△ABC中，已知A=60°,C=45°,c=20cm,解三角形(邊長精確到1cm).

練習(xí)2.在△ABC中，已知a=20cm,b=11cm,B=30°,解三角形(角度精確到1°，邊長精確到1cm).

設(shè)計意圖：讓學(xué)生在初步掌握了正弦定理的應(yīng)用后，獨立運用知識完成練習(xí)，鞏固強化概念的生成和應(yīng)用，將新知識進行內(nèi)化。

3.解決引例問題

分析：要測量兩點A、B之間的距離，所求的邊AB的對角是已知的，又已知三角形的一邊AC，根據(jù)三角形內(nèi)角和定理可計算出邊AC的對角，根據(jù)正弦定理，可以計算出邊AB。

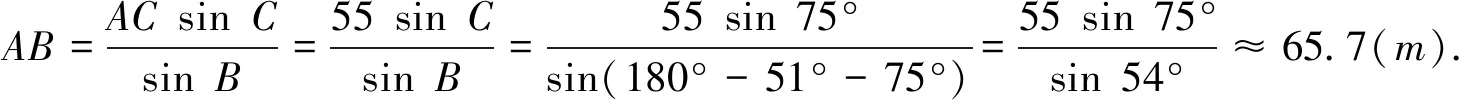
答：A,B兩點間的距離為65.7米。

(五)歸納小結(jié)，知識升華

(六)作業(yè)布置

1.必做題：教材10頁A組：第1題，第2題；

2.選做題：用“外接圓法”證明正弦定理，看看你有什么新的發(fā)現(xiàn)。

適當(dāng)?shù)淖鳂I(yè)布置可以使學(xué)生在課下鞏固所學(xué)知識，作業(yè)有必做題與選做題，學(xué)生可以自主選擇，主動探究學(xué)習(xí)，親身經(jīng)歷知識獲得的過程。

(七)板書設(shè)計

2.證明方法：作高法

3.解三角形：①已知兩角和一邊；②已知兩邊和其中一邊的對角，板書的設(shè)計使學(xué)生對上課所學(xué)的知識一目了然，并能清楚地知道重難點，做到心中有數(shù)。

五、說課綜述

以上是我對《正弦定理》這節(jié)課的認(rèn)識和教學(xué)過程的設(shè)計，在整個課堂中，我引導(dǎo)學(xué)生回顧直角三角形中的勾股定理，作為探索三角形邊角關(guān)系的出發(fā)點，并把所得結(jié)論推廣到任意三角形中去，使學(xué)生進一步認(rèn)識正弦定理，采用“特殊—歸納—猜想—證明”的數(shù)學(xué)思想方法并證明定理，逐步深化學(xué)生的認(rèn)知活動，讓學(xué)生既掌握了知識，又學(xué)會了方法。

總之，對課堂的設(shè)計，我始終按照新課標(biāo)要求，堅持以學(xué)生為主體，以教師主導(dǎo)，并從各種實際出發(fā)，引導(dǎo)學(xué)生不斷積極探索新知，鍛煉學(xué)生思維，有計劃地培養(yǎng)學(xué)生觀察能力、應(yīng)用知識能力和創(chuàng)造力。以上就是我對本節(jié)課的理解與設(shè)計，不足之處，請各位老師批評指正，我的說課到此結(jié)束，謝謝大家！