鐵磁性納米片間相互作用對其微波磁性的影響

李 艷, 陳將偉, 謝國治, 陶志闊

(南京郵電大學 電子科學與工程學院，南京 210003)

由于吸波材料能夠有效吸收電磁波，并減少電磁波反向散射，有望用于飛行器的隱身技術、微波暗室、電磁兼容等方面而受到人們的廣泛關注[1-3].理想的吸波材料應滿足如下性能：吸波頻段寬、吸收能力強、質量輕、吸波涂層厚度薄.因此，人們致力于開發具有高磁導率和高磁損耗的新型微波吸收材料[4-6].在鐵磁性納米片中，交換能、偶極能和各向異性能之間存在著復雜的競爭.因此,這種結構化介質的靜態和動態性能與構成材料的固有磁特性、各個元素的形狀尺寸及納米片間相互作用等有著密切的關系[7-9].已有研究表明,具有低于臨界厚度的單層鐵磁薄膜可以顯示一個良好限定的均勻鐵磁共振模型[10].坡莫合金納米帶通常存在兩種共振模式，“塊體”共振模式和“邊緣”共振模式[11-12].矩形鐵磁性納米片長寬比越大，則“塊體”模式的強度越強.隨著矩形比逐漸減小，低頻共振峰峰高會變得大于高頻共振峰峰高，最終出現一個明顯共振峰和一些微小共振峰[13].但關于兩納米片的相對位置、納米片間距、磁各向異性方向對鐵磁性納米片微波磁性影響的研究鮮有報道.本文提出了多納米片結構，其具有較強的形狀各向異性和高磁導率,通過調節納米片的相對位置、納米片間距、磁各向異性方向展寬磁共振峰的峰寬，使其能有效地工作在一個較寬的吸收頻帶.

1 微磁學理論及模擬方法

在微磁學模擬中，磁介質表示為宏觀連續體，其特征取決于依賴空間和時間的磁化強度M(ri,t)，且在恒溫下磁化矢量模為常數，即|M(ri,t)|=Ms.通過求解 Landau-Lifshitz-Gilbert (LLG) 常微分方程獲得磁化分布的演變.

(1)

式中：M(ri,t)為磁化強度矢量；γ為旋磁比(γ取2.21×105m/(A·s))；α為阻尼系數；Heff(ri,t)為有效場(包括交換場、磁晶各向異性場、退磁場和外磁場)，它是吉布斯自由能對磁極化強度的負數微分，即

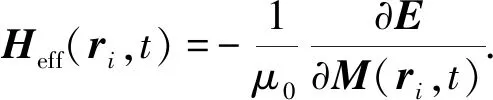
(2)

吉布斯自由能E由4個能量項組成(忽略彈性勢能和表面各向異性能)：交換能、磁晶各向異性能、退磁能和Zeeman能(外場能)[14-15].首先在未加外磁場情況下，通過求解時域中的磁化運動方程(LLG)，獲得磁體的靜態磁矩分布.然后，采用靜態磁矩分布作為初始狀態，計算鐵磁性納米片的高頻響應.為了計算與弱交變外磁場δh(t)相關的線性磁響應δm(ri,t)，磁化強度和有效場分別由靜態部分和小的動態擾動組成[7-12].

M(ri,t)=Meq(ri)+δm(ri,t)，

(3)

Heff(ri,t)=Heq(ri)+δh(t)+Heq(δm(ri,t)).

(4)

且Heq(ri)=Heff(Meq(ri))，|δm(ri,t)|?|Meq(ri)|，|Heq(δm)|?|Heq(ri)|，|δh(t)|?|Heq(ri)|.在一階動態擾動的限制條件下，將式(3)、(4)代入式(1)得到

(5)

對于一個給定的弱交變場δh(t)，式(4)的解允許訪問交變磁化強度δm(ri,t)，其中交變磁化強度δm(ri,t)是交變外磁場δh(t)和磁化率χ(ri,t)的卷積.

δm(ri,t)=χ(ri,t)*δh(t).

(6)

通過快速傅里葉變換(Fast Fourier Transform，FFT)可以將式(6)變換到頻域，

δm(ri,ω)=χ(ri,ω)*δh(ω).

(7)

為了減小非線性行為，通過外加一個弱的交變磁場激勵系統來獲得磁化率.

δh(t)=7.96exp(-7.675t).

式中：t為時間，ns；h為磁場強度，A/m.上式通過快速傅里葉變換得到

δh(ω)=7.96/(7.675+2πiω).

其中，ω為交變磁場的固定頻率，GHz.這種形式有高達20 GHz的頻率響應，可計算得到這個頻率的磁化率[10-12]，且該交變磁場在矩形鐵磁性納米片內是一個空間均勻的場.

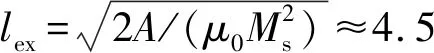
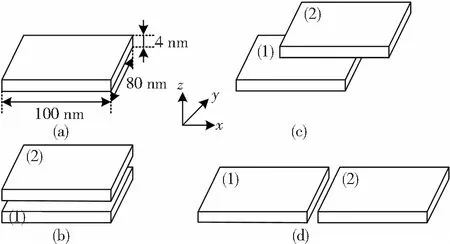
圖1 仿真對象模型圖:(a) 單個矩形納米片模型 ；(b) 上下平行排列的兩個矩形納米片模型 ；(c) 上下平行且有相對位移的兩個矩形納米片模型； (d) 左右平行排列的兩個矩形納米片模型

Fig.1 Simulation object model: (a) single rectangular nanosheet model；(b) two rectangular nanosheet models arranged parallel to each other；(c) two rectangular nanosheet models arranged up and down with relative displacements；(d) two rectangular nanosheet models arranged parallel to each other

2 結果與討論

首先，計算單個矩形鐵磁性納米片的靜態磁矩分布和磁譜，如圖2所示.從圖2(a)可以看出，矩形鐵磁性納米片長軸中間部分的磁矩偏離長軸，并與長軸呈45°排列，而長軸兩端的磁矩趨向于沿短軸方向，且納米片所有區域中的相鄰磁矩彼此幾乎都趨于平行.在鐵磁性納米片體系中，磁晶各向異性有利于磁矩平行或反平行于易軸，交換作用使相鄰磁矩平行排列，而退磁相互作用使得矩形鐵磁性納米片兩端的磁矩偏離矩形鐵磁性納米片的長軸.各向異性能、交換能和退磁能的競爭最終導致一個不均勻的磁化狀態，見圖2(a).

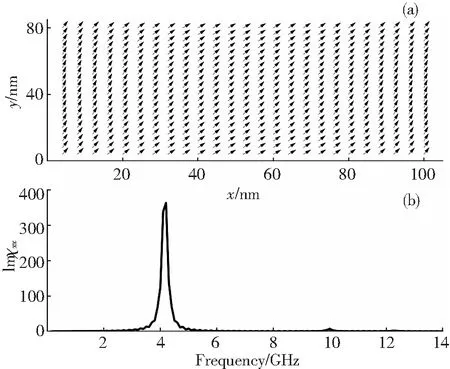
圖2 單個矩形鐵磁性納米片的靜態磁矩分布(a)和磁化率(Imχxx)虛部(b)

Fig.2 Equilibrium configuration (a)and imaginary part of susceptibility (Imχxx)(b)of single rectangular ferromagnetic nanosheets

從圖2(b)可以看出，磁譜由一個頻率為4.2 GHz的強共振峰和一個頻率為10 GHz的弱共振峰組成，這是由納米片邊緣和納米片中間的局部有效場變化引起的.

圖3為相距分別為1、2、3、4、5 nm的上下平行排列的兩個矩形鐵磁性納米片的靜態磁矩分布和磁譜.圖3(a)、(d)、(g)、(j)、(m) 分別為相距1、2、3、4、5 nm的上下平行排列的兩個矩形鐵磁性納米片的下部分，圖3(b)、(e)、(h)、(k)、(n) 分別為相距1、2、3、4、5 nm的上下平行排列的兩個矩形鐵磁性納米片的上部分.比較圖3(a)、(d)、(g)、(j)、(m)，發現其靜態磁矩分布非常相似，納米片長軸中間部分的磁矩都傾向于沿長軸方向排列，納米片長軸兩端的磁矩稍偏離長軸方向，且相鄰磁矩彼此幾乎趨于平行.同樣，圖3的(b)、(e)、(h)、(k)、(n) 與圖3(a)、(d)、(g)、(j)、(m)的靜態磁矩分布相似，只是磁矩方向相反.這是交換能、退磁能、各向異性能共同決定的總自由能取最小值的體現.圖3(c)、(f)、(i)、 (l)、(o)分別為相距1、2、3、4、5 nm的上下平行排列的兩個矩形鐵磁性納米片的磁譜，可以看到，磁譜都是由一個較低頻率的強共振峰和一個較高頻率的弱共振峰組成，這是由納米片邊緣和納米片中間的局部有效場變化引起的，并且，隨著兩矩形鐵磁性納米片之間距離的增加，磁譜的主共振峰隨之增大，接近于單個矩形鐵磁性納米片的磁譜的主共振峰(圖2(b)).這可能是由于隨著兩納米片之間距離變大，兩納米片之間的相互作用變小，當兩納米片間的距離增大到一定程度，它們之間不存在相互作用，相當于兩個單個矩形鐵磁性納米片.相距4、5 nm時，強共振峰與單個矩形鐵磁性納米片的磁譜的主共振峰(4.2 GHz)相同.說明從相距大于4 nm時，兩矩形鐵磁性納米片相當于兩個彼此獨立的單矩形鐵磁性納米片.

圖4為磁各向異性方向分別呈0°、30°、45°、60°、90°的上下平行排列的兩個矩形鐵磁性納米片(兩納米片上下相距1 nm)的靜態磁矩分布和磁譜.圖4(a)、(d)、(g)、(j)、(m)分別為磁各向異性方向呈0°、30°、45°、60°、90°的上下平行排列的兩個矩形鐵磁性納米片的下部分(即圖1(b)中的(1)部分)的靜態磁矩分布.圖4(b)、(e)、(h)、(k)、(n)分別為磁各向異性方向呈0°、30°、45°、60°、90°的上下平行排列的兩個矩形鐵磁性納米片的上部分(即圖1(b)中的(2)部分)的靜態磁矩分布.從圖4(a)、(b)、(d)、(e) 的靜態磁矩分布中可以看出，除磁矩方向不同外，磁矩幾乎都傾向于沿長軸方向排列，只有納米片長軸兩端的磁矩稍微偏離長軸方向.圖4(c)、 (f)分別為磁各向異性方向分別呈0°、 30° 的上下平行排列的兩個矩形鐵磁性納米片的磁譜， 兩圖中磁譜都只有一個較低頻率的共振峰，且頻率和峰值幾乎相同.這說明當改變兩個矩形鐵磁性納米片的磁各向異性方向所呈角度較小時，對矩形鐵磁性納米片的磁性能的影響可以忽略不計.從圖4(g)、(j)、(m)的靜態磁矩分布可以發現，所有磁矩都偏離長軸方向且與長軸呈45°排列.圖4(h)、(k)、(n)中的靜態磁矩分布也是如此，只是磁矩的方向與圖4(g)、(j)、(m)中磁矩的方向相反.圖4(i)、(l)、(o)分別為磁各向異性方向分別呈45°、60°、90°的上下平行排列的兩個矩形鐵磁性納米片的磁譜.比較圖3(c)、(f)與(i)可以發現，其磁譜都由一個強共振峰和多個弱共振峰組成，且主共振峰移動到一個較高的頻率8.5 GHz上.說明兩個矩形鐵磁性納米片的磁各向異性方向所呈角度由45°增加到90°時，對矩形鐵磁性納米片的磁性能的影響變化不大.由上述結果可以得出，隨著兩個矩形鐵磁性納米片的磁各向異性方向所呈角度由30°增加到45°，其磁譜的主共振峰隨之由2.2 GHz增加到8.5 GHz.

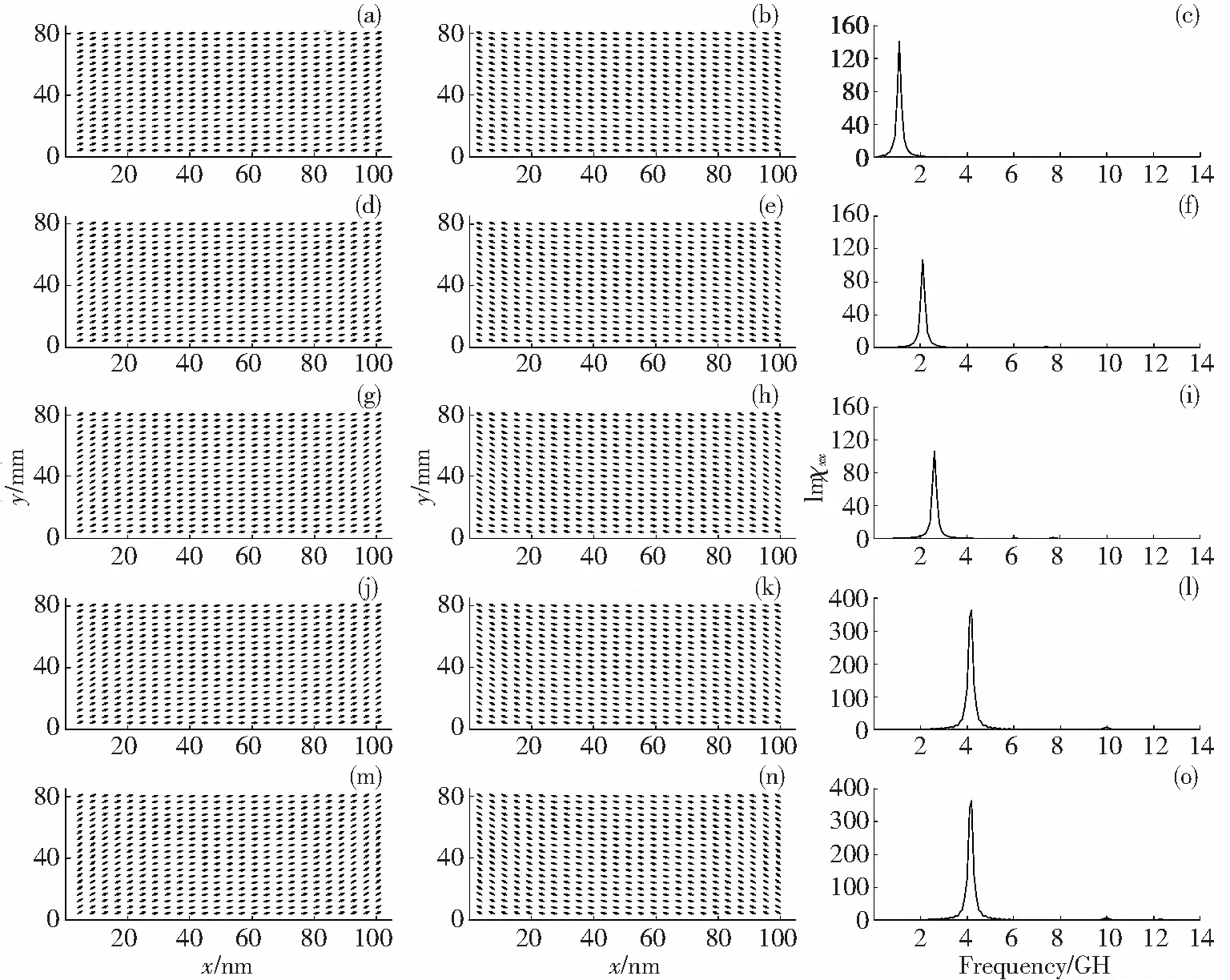
圖3 圖1中(b)模型的靜態磁矩分布和磁譜

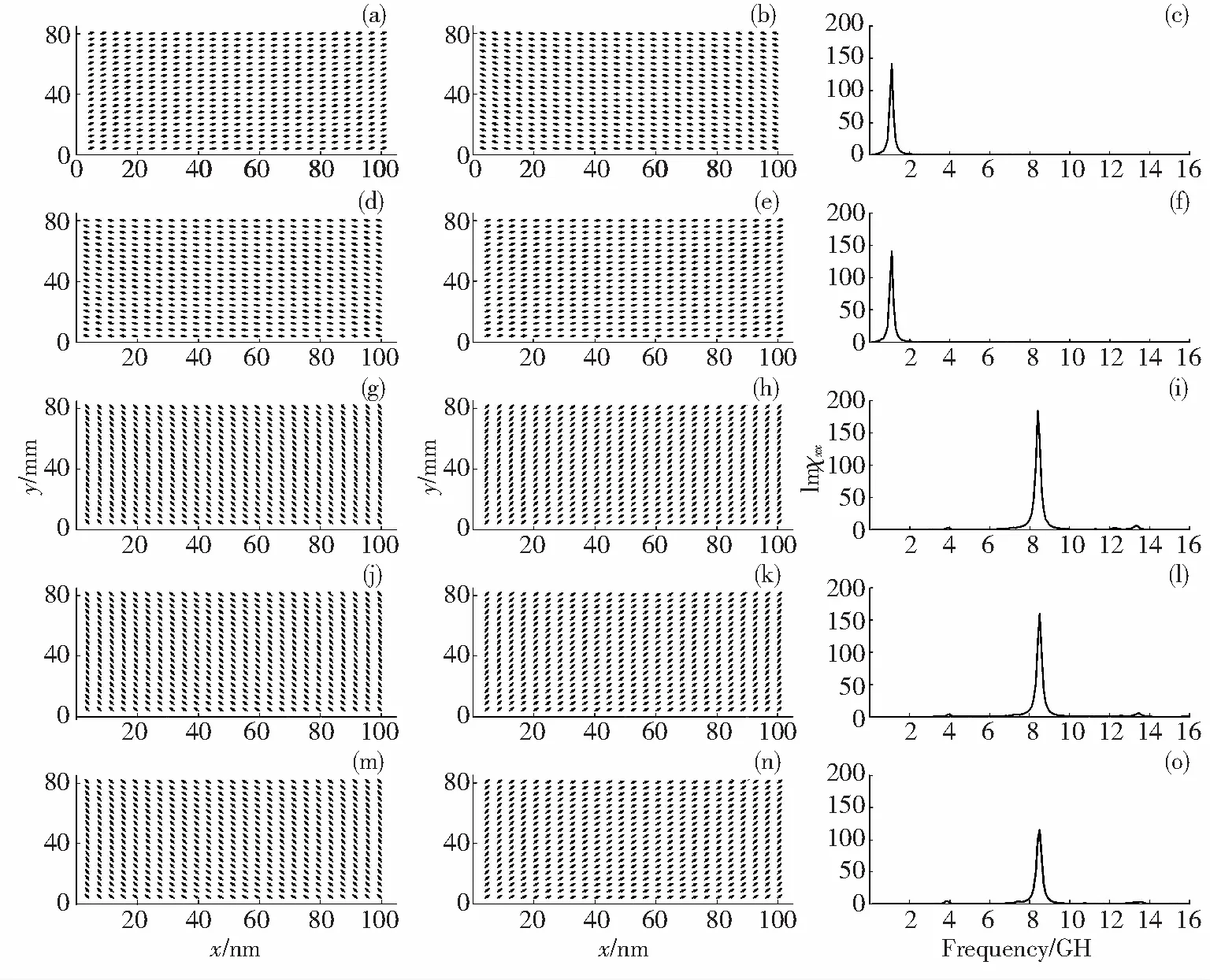
圖4 磁各向異性方向分別呈0°、30°、45°、60°、90°的上((b)、(e)、(h)、(k)、(n))下((a)、(d)、(g)、(j)、(m))平行排列的兩個矩形鐵磁性納米片的靜態磁矩分布和磁譜((c)、(f)、(i)、(l)、(o))

Fig.4 Equilibrium configurations and the imaginary parts of susceptibility Imχxxof two parallel rectangular ferromagnetic nanosheets with the magnetic anisotropic directions at 0°, 30°, 45°, 60°and 90°, respectively

圖5為磁各向異性方向分別呈0°、30°、45°、60°、90°的上下平行排列且有相對位移(上部分相對下部分x軸位移40 nm，y軸位移48 nm)的兩個矩形鐵磁性納米片(兩納米片上下相距1 nm)的靜態磁矩分布和磁譜.圖5(a)、(d)、(g)、(j)、(m)分別為磁各向異性方向呈0°、30°、45°、60°、90°的上下平行排列且有相對位移的兩個矩形鐵磁性納米片的下部分(即圖1(c)中的(1)部分)的靜態磁矩分布.圖5(b)、(e)、(h)、(k)、(n)分別為磁各向異性方向呈0°、30°、45°、60°、90°的上下平行排列且有相對位移的兩個矩形鐵磁性納米片的上部分(即圖1(c)中的(2)部分)的靜態磁矩分布.從圖5(a)、(b)、(d)、(e)的靜態磁矩分布可以發現，納米片短軸中間部分的磁矩幾乎都傾向于沿短軸方向排列，納米片短軸兩端的磁矩偏離長軸方向且與長軸呈45°排列，且這4個磁譜中的磁矩的方向一致.圖5(c)、(f)分別為磁各向異性方向分別呈0°、30°的上下平行排列且有相對位移的兩個矩形鐵磁性納米片的磁譜.比較圖5(c)與圖2(a)可以發現，圖5(c)磁譜的主共振峰移動到一個較高的頻率5.5 GHz上.說明兩納米片間的相互作用對納米片磁性能的影響有所增加.比較圖5(f)與圖5(c)發現,磁譜的主共振峰沒有明顯變化.說明當改變兩個矩形鐵磁性納米片的磁各向異性方向所呈角度較小時，對矩形鐵磁性納米片的磁性能的影響不大.

同樣， 圖5(g)、(j)、 (m)的靜態磁矩分布中納米片短軸中間部分的磁矩幾乎都傾向于沿短軸方向排列，納米片短軸兩端的磁矩偏離長軸方向且與長軸呈45°排列，它們磁譜中磁矩的方向一致且彼此平行.但是，圖5(h)、(k)、(n)的靜態磁矩分布中納米片長軸中間部分的磁矩幾乎都傾向于沿長軸方向排列，納米片長軸兩端的磁矩偏離長軸方向且與長軸呈45°排列，它們磁譜中磁矩的方向一致且彼此平行.圖5(i)、(l)、(o)分別為磁各向異性方向分別呈45°、60°、90°的上下平行排列且有相對位移的兩個矩形鐵磁性納米片的磁譜.從圖5(i)中可看出，磁譜虛部存在3個共振峰，頻率分別為3.6、5.1、7.5 GHz，它們的峰寬約為1.5 GHz.圖5(l)與圖5(i)比較，共振峰的數目相同，頻率分別為3.6、5.1、7.2 GHz，其中頻率為3.6 GHz的共振峰峰值比圖5(i)中頻率為3.6 GHz的共振峰峰值高.圖5(n)磁譜的共振峰頻率分別為3 、4.5、5.5 GHz，由于頻率相近而產生交疊，在一定意義上相當于增大了共振峰的峰寬，整體峰寬約為4 GHz.本文推測兩個矩形鐵磁性納米片的磁譜存在多個共振峰可能是由于其內部存在多個不同大小的局域有效場，由于改變兩納米片的相對位置以及磁各向異性方向，破壞了納米片原有較為均勻的有效場，導致了更加不均勻的場強分布.

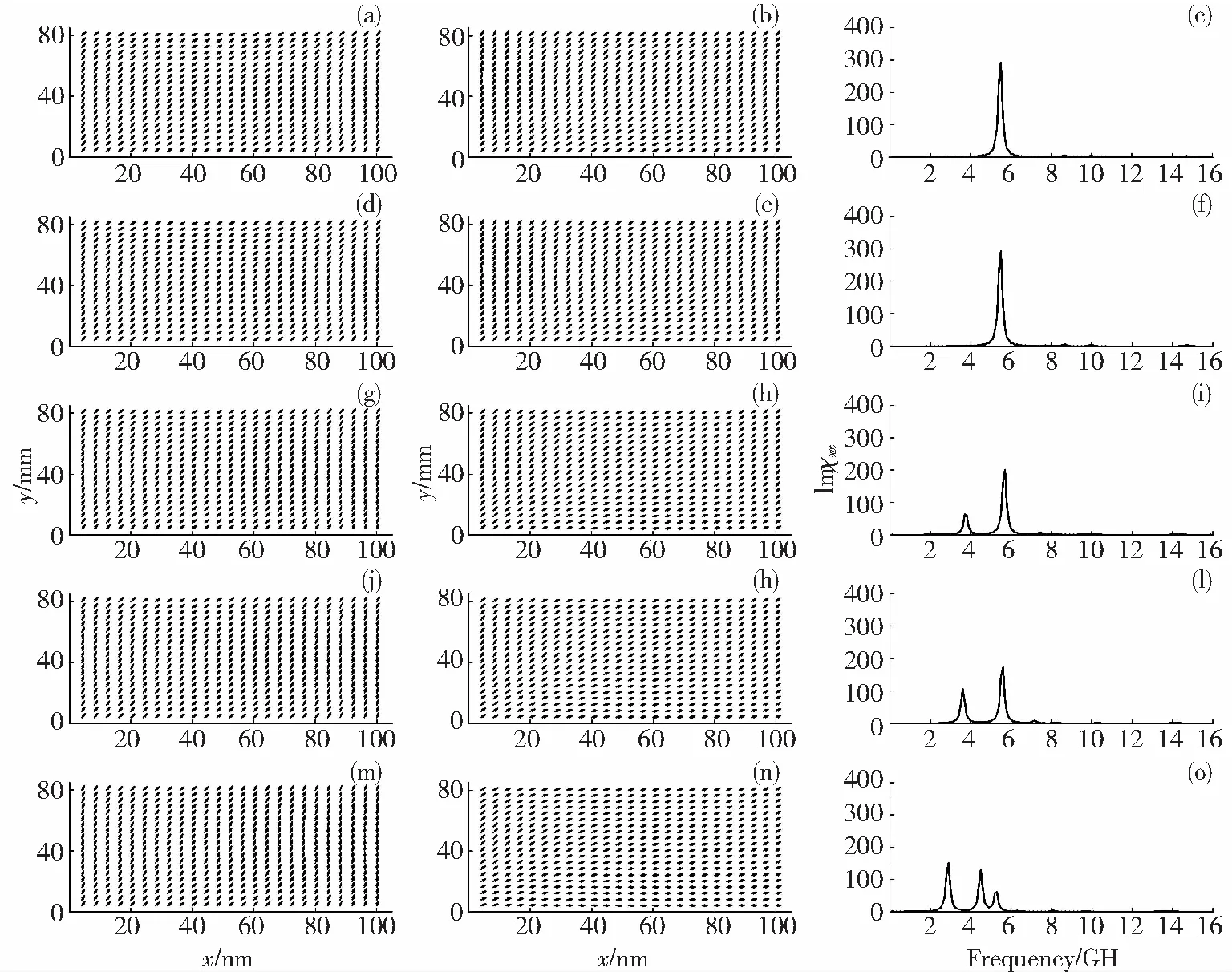
圖5 磁各向異性方向分別呈0°、30°、45°、60°、90°的上((b)、(e)、(h)、(k)、(n))下((a)、(d)、(g)、(j)、(m))排列且有相對位移的兩個矩形鐵磁納米片的靜態磁矩分布和磁譜((c)、(f)、(i)、(l)、(o))

Fig.5 Equilibrium configurations and the imaginary parts of susceptibility Imχxxof the two rectangular ferromagnetic nanosheets with relative displacement and the magnetic anisotropy directions at 0°, 30°, 45°, 60°and 90°, respectively

圖6為磁各向異性方向分別呈0°、30°、45°、60°、90°的左右平行排列的兩個矩形鐵磁性納米片(左右兩納米片相距1 nm)的靜態磁矩分布和磁譜.圖6(a)、(d)、(g)、(j)、(m)分別為磁各向異性方向呈0°、30°、45°、60°、90°的左右平行排列的兩個矩形鐵磁性納米片的下部分(即圖1(d)中的(1)部分)的靜態磁矩分布.圖6(b)、(e)、(h)、(k)、(n)分別為磁各向異性方向呈0°、30°、45°、60°、90°的左右平行排列的兩個矩形鐵磁性納米片的上部分(即圖1(d)中的(2)部分)的靜態磁矩分布.從圖6(a)、(b)、(d)、(e)的靜態磁矩分布可以發現，納米片短軸中間部分的磁矩幾乎都傾向于沿短軸方向排列，納米片短軸兩端的磁矩偏離長軸方向且與長軸呈45°排列，但兩端的磁矩方向相反，類似一個C形.圖6(c)、(f)分別為磁各向異性方向分別呈0°、30°的左右平行排列的兩個矩形鐵磁性納米片的磁譜.從圖6(c)、(f)可以發現，磁譜的主共振峰峰值高達1500，這可能是因為找到的是一個亞穩態狀態.圖6(g)、(h) 、(j)、(k) 、(m)、(n)的靜態磁矩分布中磁矩幾乎都傾向于沿長軸方向排列， 兩端的磁矩稍偏離長軸方向排列，其磁譜中的磁矩方向一致且彼此平行.圖6(i)、(l)、(o)分別為磁各向異性方向分別呈45°、60°、 90°的左右平行排列的兩個矩形鐵磁性納米片的磁譜.從圖6(i)可看出，磁譜虛部存在3個相距很近的共振峰，頻率分別為5、6、7 GHz，整體峰寬約為4 GHz.圖6(l)與圖6(i)比較，頻率為5、6 GHz的共振峰交疊在一起，鄰近的還有一個頻率為7 GHz的較小的共振峰.圖6(n)磁譜的共振峰頻率分別為2.5、4.5、5.5 GHz，由于頻率相近而產生交疊，增大了共振峰的峰寬，整體峰寬約為4 GHz.

Fig 6 Equilibrium configurations and the imaginary parts of susceptibility of the (d) model in Fig.1 in different directions of magnetic anisotropy

3 結 論

1) 相對位置、納米片間距影響兩矩形鐵磁性納米片共振峰頻率的分布，當兩矩形納米片磁各向異性方向所呈角度由0°增加到30°時，其磁性質沒有明顯的變化，而從30°到90°時，其磁性質對磁各向異性方向變化比較敏感.

2) 改變兩個矩形鐵磁性納米片的磁各向異性方向所呈角度，可顯著影響磁損耗峰的數目、強度、峰寬和頻率分布.因此，可以通過改變納米片相對位置、納米片間距及磁各向異性方向調控鐵磁性納米片的磁性質.可用于制備具有各種頻率和較寬吸收頻帶的微波吸收材料.