直線形單排管凍土帷幕平均溫度計算
劉陽輝,洪澤群,韓延廣
(1.同濟大學 地下建筑與工程系,上海 200092; 2.同濟大學 巖土及地下工程教育部重點實驗室,上海 200092; 3.上海市隧道股份有限公司,上海 200232)
在人工地層凍結技術運用過程中,需要對凍土結構進行力學分析計算,此時通常假設凍土為均質介質,選用凍土帷幕平均溫度所對應的物理力學參數作為均質假定下凍土結構材料參數。因此凍土帷幕的平均溫度不僅僅是凍結效果的重要判據,也是確定凍土力學參數,進行凍土帷幕承載力評估的重要依據。
目前常用的平均溫度求解方法有:積分法、等效截面法、經驗公式法。積分法是利用已有的溫度場解析公式,對凍土區域進行積分求解,直接求得平均溫度。由于溫度場的解析公式較為復雜,積分求解的難度較大,目前這一方法的研究較少。等效截面法是以凍結壁某一橫截面的平均溫度來代表整體凍結壁的平均溫度,諸如筆者所提出的利用等效三角形法、等效梯形法、等效拋物弓或梯形-拋物弓疊合得到的特征截面處的平均溫度來代替帷幕的平均溫度[1-4]。單排管凍結平均溫度等效計算的基礎是巴霍爾金的溫度場解析公式,因此計算準確性得到保證,但截面的選取和計算過程較為繁瑣。經驗法求解凍土帷幕的平均溫度也是一種可行辦法。陳文豹、湯志斌基于大量實測數據,給出了計算平均溫度的“成冰公式”[5],但該公式過于保守,適用性較差[6],汪仁和等學者根據數值計算結果擬合出平均溫度的計算公式[7],筆者根據等效截面計算公式形式也給出了平均溫度的經驗公式[8]。
目前,直線排管凍結溫度場解析解主要有巴霍爾金單排、雙排[9]和筆者的三排管穩態溫度場解析解[10],這些解有較高的準確性[11-12]。本文將以筆者采用邊界分離法得到的單排管凍結穩態溫度場解析解為基礎[13-14],采用積分法推導平均溫度的直接計算公式。
1 單排管凍結穩態溫度場解析解
單排管凍結的模型如圖1所示。在單排管的管間距相等,凍結管表面溫度相等情況下,筆者利用邊界分離法得到穩態溫度場解析公式(1)[14]:
(1)
式中,T(x,y)為任意點(x,y)的溫度,℃;Tf為凍結管外表面溫度,℃;ξ為凍土帷幕厚度之半,m;l為相鄰凍結管間距,m;r0為凍結管外半徑,m。
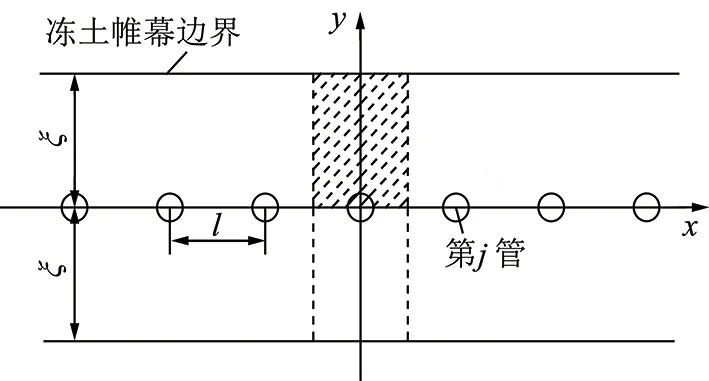
圖1 單排管凍結模型Fig.1 Model of single row-piped freezing
式(1)按照工程實際參數近似處理可以簡化成巴霍爾金的單排管凍結溫度場解析公式。
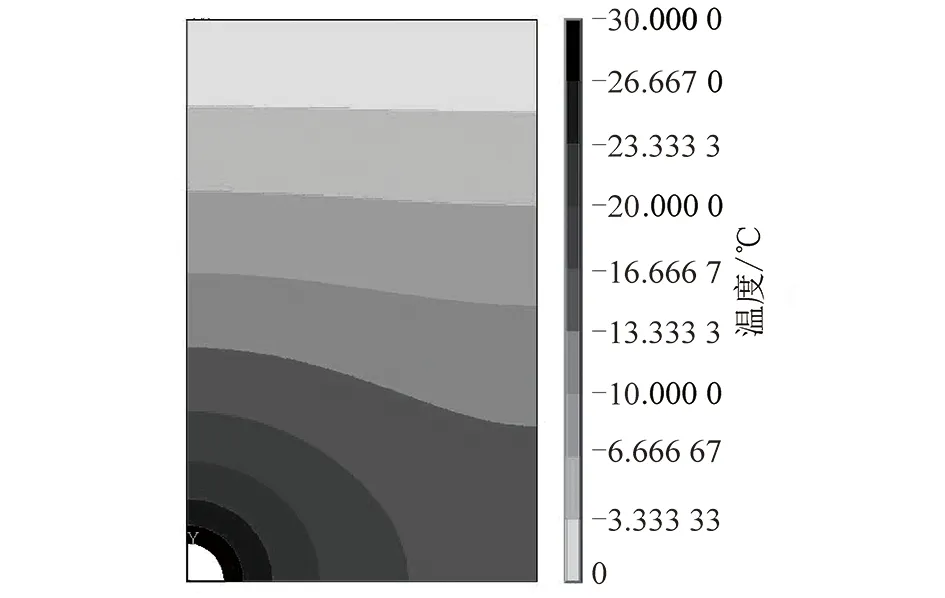
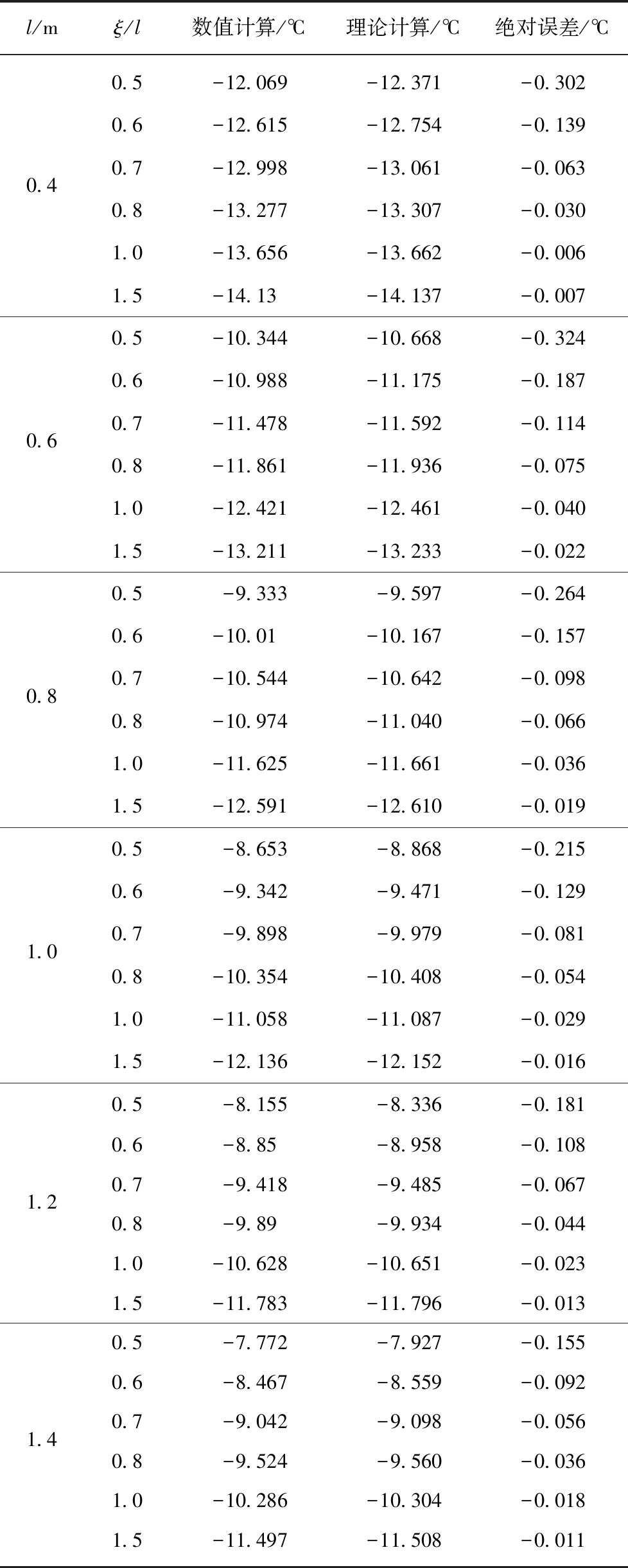
由圖1所示,根據模型的對稱性,凍土帷幕的平均溫度tcp為T(x,y)在給定區域(-l/2 (2) 把式(1)代入式(2),得到單排管凍結平均溫度的計算式。 (3) 式(3)主要問題是積分 (4) 利用貝塞特求和公式[15],得 (5) 對式(5)的積分部分進行分部積分,得到積分結果為 再次運用貝塞特求和公式,得 上式積分項在積分區間(-l/2 (6) 其中,X為區間(-l/2,l/2)內的某個實數。 將式(6)代入式(3),得到單排管凍結凍土帷幕平均溫度為 (7) 考慮到土層的凍結溫度T0的單排管凍結平均計算公式為 T0 (8) 在凍結后期,有πξ/l>1,所以ch(2πξ/l)遠大于cos(2πX/l),得ch(2πξ/l)-cos(2πX/l)≈ch(2πξ/l)-1,式(8)可簡化為 (9) 在上述推導過程,積分區域包含了凍結管部分,實際土層的平均溫度的計算不應包含上述區域。同時,由于T(x,y)在凍結管圓心(0,0)處的取值趨于無窮,無法確定凍結管處的溫度對積分結果的影響。因此需要對式(9)進行修正,減小偏差。 由于曲線積分較為困難,修正將采用已有積分策略對矩形區域(-r0 (10) 上述修正是對矩形區域(-r0 本文推導的平均溫度計算公式是基于單排管凍結的穩態解析解,并根據實際工程對一些參數進行了簡化,因此需要對解析公式的準確性進行研究。本文ANSYS進行熱學數值計算,來研究公式的準確性和精度,確定計算公式的適用范圍,即ξ/l滿足什么條件時,理論計算較為精確。 考慮到單排管凍結布管形式的對稱性,計算選取1/4區域,如圖2所示。土性參數選取根據《上海地區人工凍土物理力學性能試驗及其應用技術研究報告》[16],主要參數的取值初始溫度為-20 ℃;凍土導熱系數為172 W/(m·K);未凍土導熱系數為122 W/(m·K);比熱容為1.65 kJ/(kg·℃)。凍結參數根據常見情況,取Tf=-30 ℃,T0=0 ℃,r0=0.054 m,選用管間距l=0.4,0.6,0.8,1.0,1.2,1.4 m,考慮ξ/l=0.5,0.6,0.7,0.8,1.0,1.5共6種凍結發展狀態。圖3為l=1.0 m,ξ/l=0.8計算結果的溫度云圖。理論計算采用式(11),計算結果見表1,其中絕對誤差為理論計算與數值計算結果的差值。 圖2 計算模型Fig.2 Calculation model 圖3 l=1.0 m,ξ/l=0.8的溫度云圖Fig.3 Contour plot of calculation results 將修正公式和數值計算的結果進行比較,如圖4所示。 根據計算結果及對比,得到以下結論。 (1)理論計算結果與數值計算結果較為吻合。所完成的算例中,平均溫度的誤差小于0.5 ℃,隨著凍土厚度的發展,理論計算結果與數值計算結果的差值逐漸減小。 (2)針對第2節提出得矩形修正區域與凍結管的差集,在常見布管參數條件下,該區域對計算結果的影響是有限的。這片區域的土體溫度約為-30 ℃,面積約為0.001 3 m2。取最不利情況(凍土區域最小),l=0.4 m,ξ=0.2 m計算。這片區域造成的誤差約為0.47 ℃,隨著凍土厚度的發展,誤差逐漸減小。同時,這塊區域對理論計算的影響是提高平均溫度,使計算結果偏向安全。因此采用矩形區域進行修正是可行的。 表1 計算結果Table 1 Calculation results 圖4 結果對比Fig.4 Calculation results (1)基于單排管凍結穩態溫度場解析解,本文采用積分法推導出凍土帷幕平均溫度的直接計算公式,并對在凍結管附近的計算進行了修正。 (2)根據算例,隨著凍土厚度的發展(相對厚度的增大),理論計算結果與數值計算結果的差值迅速減小到0.5 ℃以內,當相對厚度大于0.6時,對比計算結果的差值小于0.2 ℃。當相對厚度為1及以上時,差值小于0.1 ℃。通過數值模擬驗證了平均溫度計算公式的準確性,也說明公式簡化和修正的合理性,公式計算的誤差滿足工程應用的要求。2 單排管凍結平均溫度的計算
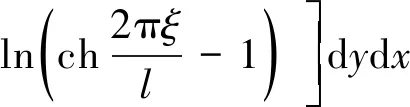


3 解的準確性


4 結 論

