BDS精密單點定位在橋梁變形監測中的應用

劉明亮,丁克良,劉亞杰,于龍昊,鮑東東

(北京建筑大學 測繪與城市空間信息學院,北京 100044)

0 引 言

橋梁變形會使橋梁的整體結構發生損壞,導致橋梁發生破裂或者坍塌,會對出行的人們的生命安全造成威脅．因此橋梁變形監測不僅可以實時掌握橋梁的整體變形情況和結構損傷,為橋梁的維護和修繕提供有效的數據支撐,還可以避免不必要的人員傷亡和經濟損失．

傳統的橋梁變形監測方法主要有全站儀測量、水準測量、攝影測量、GPS測量以及地基干涉雷達等,其中GPS監測可以獲取監測點的高精度三維坐標,已經成為目前主要的監測手段．與傳統方法相比,精密單點定位(PPP)技術只需要一臺接收機,不需要參考站,不受距離限制,只需要根據IGS提供的精密星歷以及鐘差等產品,即可獲取監測點的高精度三維坐標,具有成本低、操作簡單、節省人力資源、方便高效的優點．隨著我國北斗衛星導航系統(BDS)逐步完成亞太地區的組網,BDS已經具備獨立定位導航能力,利用BDS進行建筑物變形監測將是必然趨勢．自從BDS具備導航定位能力以來,國內很多學者對BDS的PPP技術做了研究分析,劉行波等[1]對BDS實時PPP進行了精度分析,發現與GPS實時PPP精度相當;李超等[2]對不同時長的BDS的PPP進行了精度分析,表明時長越長精度越高;王閱兵等[3]做了BDS與GPS的PPP精度的對比分析,發現BDS的PPP精度水平方向為1～2 cm,垂直方向為3～4 cm,但是隨著BDS這幾年的完善,精度一定會有所提高．

本文對某現役大型公路橋梁進行變形監測,利用采集到的1 Hz的GPS/BDS數據,基于PPP技術,分別對采集數據做靜態和動態處理,分析橋梁動態變形情況下BDS的PPP精度,為今后橋梁變形監測提供一種新的監測方法．

1 精密單點定位(PPP)

PPP技術是指利用單臺接收機,通過載波相位和碼偽距方式,采用精密星歷、高精度衛星軌道和鐘差產品,通過一些誤差改正模型或者參數估計的方法,精細考慮與衛星端、信號傳播路徑及接收機端有關誤差對定位的影響,實現高精度定位的一種方法[4-5]．

1.1 碼觀測方程

全球衛星導航系統(GNSS)接收機的基本觀測量就是計算出衛星到接收機的傳播時間,利用計算出來的傳播時間和光速相乘,即可得到碼觀測方程或者偽距觀測方程[6]:

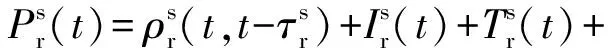
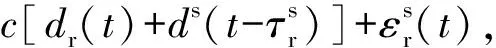
(1)

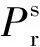
1.2 載波相位觀測方程

載波相位的觀測方程表示為[7-8]

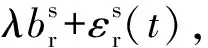
[φr(t0)-φs(t0)].

(2)

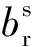
1.3 函數模型

消電離層組合模型是PPP中常用的模型,本次做BDS數據解算就是采用雙頻無電離層組合模型,根據文獻[6]可知模型為

dr(hd(P(B1,B2)))+dmult(P(B1,B2))+

εP(B1,B2).

(3)

=ρ+c·dt+dtrop+NIF+BIF+

dmult(Φ(B1,B2))+εΦ(B1,B2),

(4)

其中:

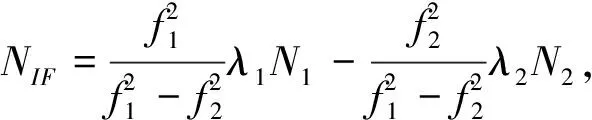
(5)

(6)

式中:PIF、φIF分別為無電離層組合的偽距和相位觀測值(m);f1、f2分別為B1和B2載波相位觀測值的頻率(MHz);λ1和λ2分別為B1和B2載波相位觀測值的波長(m/周);N1和N2分別為B1和B2載波相位觀測值的模糊度(周);ρ為衛星到地球的幾何距離(m);c為真空中的光速(m/s);dt為接收機鐘差(s);dtrop為對流層延遲誤差(m);NIF為雙頻無電離層組合模糊度(m);BIF為雙頻無電離層組合初始相位偏差(m);其余項為載波的相位偏差、硬件延遲誤差以及多路徑效應;

1.4 參數隨機模型

在PPP中,主要的參數有:三維坐標位置、接收機鐘差、對流層天頂濕延遲和模糊度參數．本文所用的采集數據沒有發生周跳,則整周模糊度為常數,其余參數的確定采用卡爾曼濾波的隨機模型．離散一階高斯馬爾可夫過程可表示為[7]:

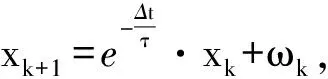
(7)

式中:x為狀態向量;τ為相關時間;ω為零均值的白噪聲序列;Δt為采用間隔;

可得到狀態轉移矩陣和動態噪聲方差陣:

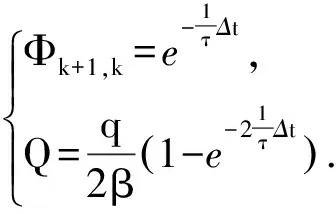
(8)

式中,q為譜密度或者動態噪聲的方差.

當τ→0時,一階高斯馬爾可夫過程模型為純白噪聲:

(9)

當τ→∞時,為純隨機游走過程:

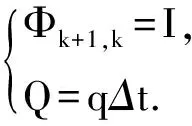
(10)

對于靜態PPP,三維坐標的參數方差陣可以表示為

(11)

式中:qφ,qλ,qh分別為緯度、精度、高程方向的譜密度;Rm,Rn分別為子午圈曲率半徑和卯酉圈曲率半徑;h為測站大地高;

接收機鐘差參數方差陣為隨機游走時表示為

Qclk=[qdtΔt],

(12)

為純白噪聲時表示為

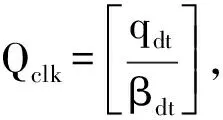
(13)

式中:qdt為接收機鐘譜密度;βdt為接收機鐘差參數的阻尼系數;

對流層天頂濕延遲通常表示為隨機游走模型.

Qtrop=[qtropΔt],

(14)

式中,qtrop為接收機鐘譜密度,由流層延遲變化率決定;

在參數處理時,模糊度當做常數處理,表示為:

QN=0.

(15)

2 工程實例分析

2.1 北斗靜態PPP精度分析

數據利用實際工程監測數據,監測時間為2017年4月8日上午7:00—9:00,選取最后一小時監測數據進行處理,監測目標為北京市某現役大型公路橋梁,在橋梁一側布設三個監測點(JCD1,JCD2,JCD3),并在橋下布設了一個基準點(JZD1),采用可以接收BDS數據的華測接收機,采樣間隔設置為1 s,連續監測一小時左右,監測時需要至少可以接收到4顆以上BDS衛星．

為了驗證BDS靜態PPP精度,采用GAMIT軟件對三個監測點進行BDS端基線解算,并用GAMIT里面的網平差模塊GLOBK進行網平差．該軟件最新版本10.61可以對BDS數據進行解算,采用精密星歷和高精度起算點,精度可達毫米級,與解算GPS數據精度基本一致．本文以GAMIT解算出來的網平差坐標作為參考基準檢驗BDS靜態PPP定位結果精度．

RTKLIB軟件是一個用于GNSS的開放源程序包,可實現標準和精確定位．本文使用最新版本的RTKLIB2.4.3并對其開源代碼做本文需要的改動，以實現三個監測點的BDS靜態PPP坐標解算．解算之前需檢查監測區域上空衛星分布情況,如圖1所示.

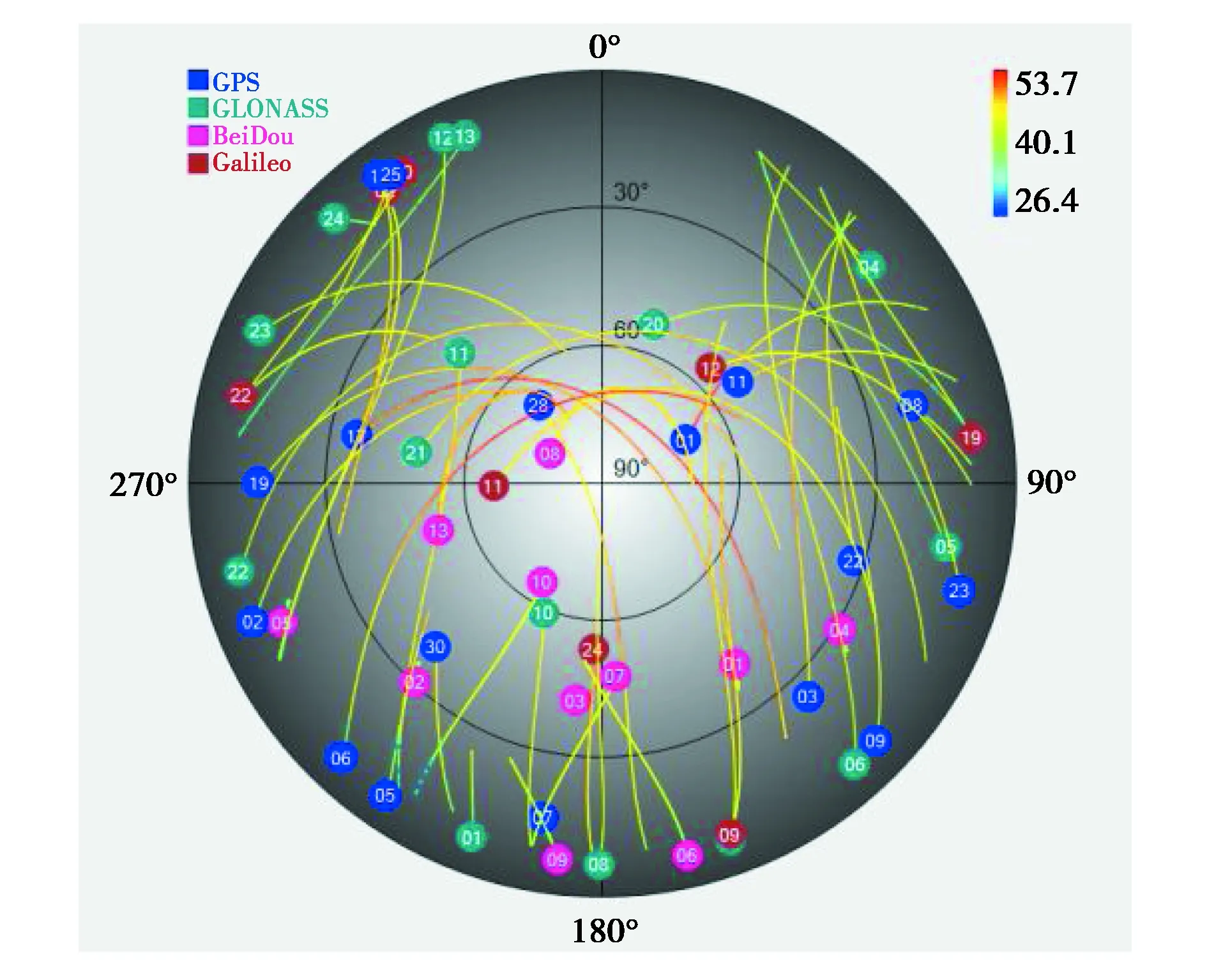
圖1 監測區域衛星視圖

由圖1所知,變形監測時能同時接收到的GPS和BDS衛星都大于4顆,監測環境良好,能實現高精度定位．

對三個監測點做BDS靜態PPP處理,對比分析這三個監測點的BDS精密定位坐標與網平差三維坐標的結果,如表1所示.

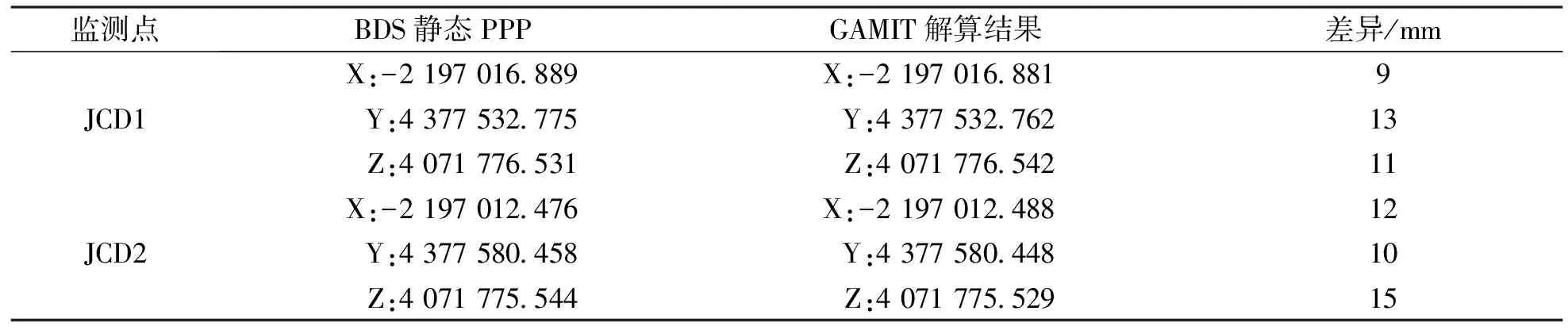
表1 北斗靜態PPP與GAMIT解算結果對比

表1(續)

由表1所知,在連續 1 h的變形監測中,BDS的PPP水平向精度可以達到1～1.5 cm,豎直向精度可以達到1～2 cm．

2.2 北斗動態PPP精度分析

由于篇幅限制,且JCD1和JCD3是對稱放置,只需要對JCD1和JCD2做數據解算處理分析,為了檢驗北斗動態PPP在現役橋梁監測現場復雜環境下,進行單歷元解算BDS動態PPP能否監測出橋梁的動態變形情況,只分析解算之后的豎直向坐標,并同解算出單歷元GPS動態PPP數據,與BDS數據進行比較:

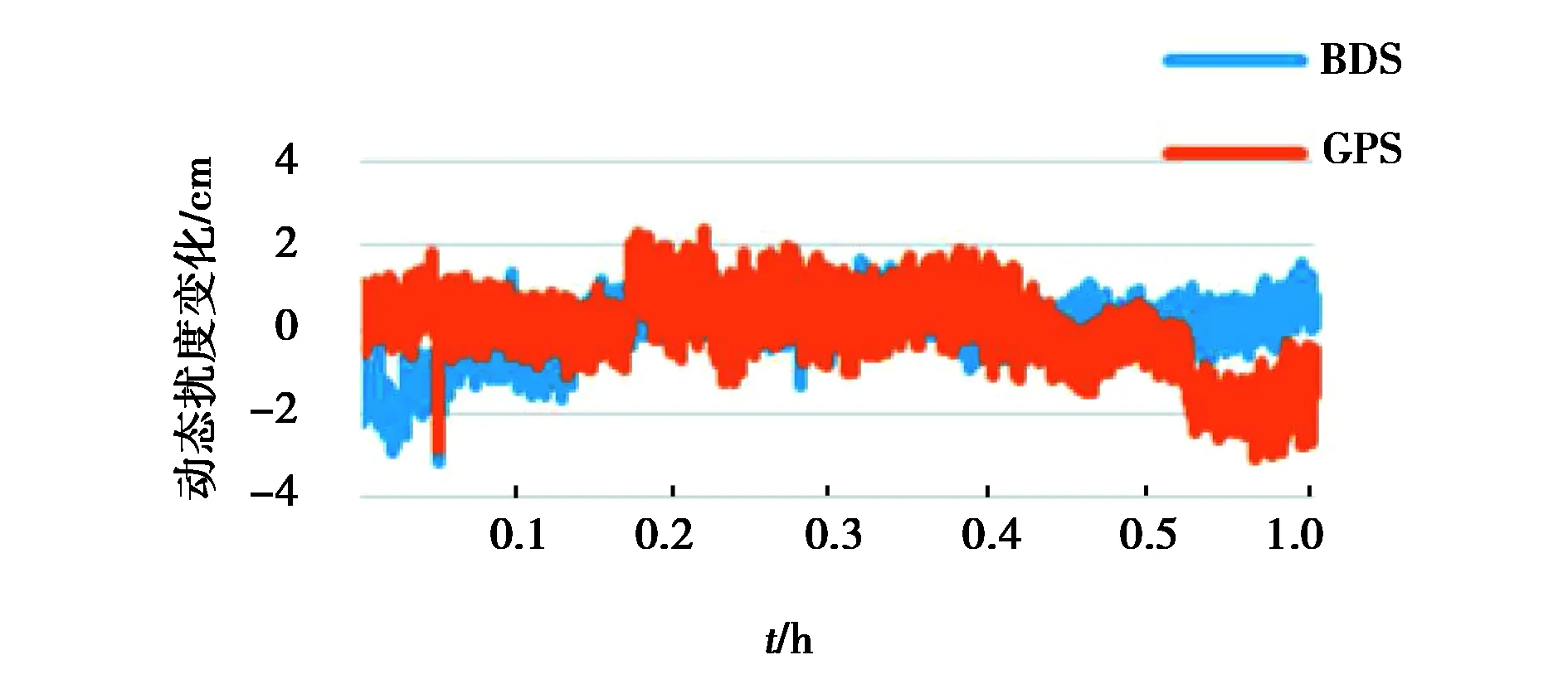
圖2 JCD1 BDS動態PPP與GPS動態PPP解算結果對比圖

如圖2所示,JCD1布設在橋梁的一端,橋梁的端側相比于橋梁中間結構較穩定,動態擾度變化趨勢較小,在監測5 min左右出現3 cm較大動態擾度變化，根據記錄人員的記錄,此刻有重型卡車通過,北斗和GPS都監測出了此時的位移變化,并且在整個監測過程中,BDS動態PPP的監測變形過程與GPS動態PPP監測變形過程一致．如圖3所示,JCD2布設在橋梁中間,動態擾度變形相比于圖2要大,監測50分到1小時之間的10 min,根據記錄人員的記錄,這段時間橋上發生了擁堵,但是橋梁的端側沒有擁堵,所以JCD2此時動態擾度變形大而且頻繁,圖2此刻沒有發生太大變形,BDS動態PPP和GPS動態PPP都監測出了整個監測過程橋梁動態擾度變形情況,并且監測變形過程一致．

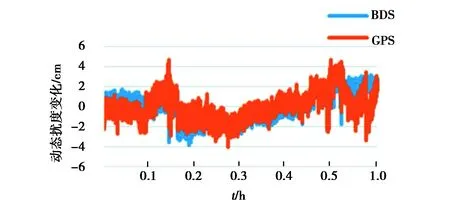
圖3 JCD2 BDS動態PPP與GPS動態PPP解算結果對比圖

綜上所述，BDS動態PPP可以滿足大型橋梁厘米級的動態變形監測,能監測出大型車輛經過橋梁時所造成的厘米級變形,對于毫米級高精度變形監測目前還不能滿足．

3 結束語

本文利用實際工程采集的橋梁變形監測數據,分別從BDS靜態PPP和動態PPP兩方面分析了BDS的PPP在橋梁變形監測中的精度和前景問題,得出如下結論:

1)在觀測條件較好,衛星數目較多的情況下,連續監測1 h BDS靜態和動態PPP水平和豎直向精度可以達到厘米級,能滿足厘米級變形監測精度,對于毫米級高精度變形監測還不能滿足．

2)利用BDS動態PPP做橋梁動態擾度變形監測能達到和GPS做橋梁動態擾度變形監測一樣的效果,BDS動態PPP監測變形過程與GPS監測變形過程一致,表明BDS動態PPP可以應用于大型橋梁的動態擾度變形監測．