基于遺傳算法預測2D三向的蛋白質結構
夏慧芳,郭雨珍,江宏昊
(南京航空航天大學 理學院數學系,南京 211106)
蛋白質是生命活動的重要承擔者,其空間結構在很大程度上決定了它所具有的生物學功能,因此蛋白質結構的預測對于理解蛋白質的結構與功能之間的關系,并在此基礎上進行蛋白質復性、突變體設計以及基于結構的藥物設計有著極其重要的意義[1]。蛋白質分子是由二十多種氨基酸通過共價鍵連接而成的肽鏈形成,這些肽鏈是依據什么原則形成具有一定空間結構的蛋白質分子,仍然是目前沒有解決的生物學問題[2]。隨著基因組測序工作的完成,生物學研究領域迫切需要找到一種從氨基酸序列出發,以此來預測蛋白質結構和功能的方法。在進行蛋白質結構預測過程中,研究者提出了許多模型,最簡單的是Dill等人提出的HP格點模型[3-4],該模型將所有的氨基酸分為親水性(H)氨基酸和疏水性(P)氨基酸兩類,不考慮側鏈的影響,于是氨基酸序列被定義為一個由H和P組成的序列,這個序列遵循自回避原則,可以顯示在網格上。蛋白質的天然構象是吉布斯自由能最低的構象是解決蛋白質結構預測問題的基礎。截止到現在,已經有許多近似算法應用在HP模型中,如粒子群算法[5-6]、神經網絡算法[7]、遺傳算法[8-9]等,這些算法各有各的優缺點,但至今還未發現一種算法完全好于其它算法。HP模型是一個偏理想化的模型,它需要將氨基酸鏈限制在正方形或矩形區域中,并且最大限度的將所有氨基酸只分為親水氨基酸和疏水氨基酸,但是有十幾種氨基酸并不能夠明確區分其疏水性及親水性,因此憑借HP模型來預測蛋白質結構并不符合實際。
疏水氨基酸相互作用,共價鍵和范德華力等會影響蛋白質結構的穩定性,自然狀態下的蛋白質有一個很緊湊的內部結構,范德華力在短程效應中扮演著一個不可替代的角色,由范德華力方程式所產生的能量越大,蛋白質結構將會越緊湊。因此可以考慮基于范德華力勢能解決蛋白質結構的預測問題。
遺傳算法(Genetic Algorithm ,GA)是由美國密西根大學的Holland教授和他的學生在20 世紀60年代創立的[10],該算法以遺傳機理和自然進化為基礎,模擬了自然界中發生的自適應現象,該算法被創立之后就被廣泛引用到工程問題中,現在已經發展成為一種“自適應啟發式概率性迭代式全局搜索算法”。目前,已被廣泛應用到功能優化、神經網絡、機器學習、模式識別以及圖像處理[11]等領域。
本文剩余部分按如下安排:第二章中我們介紹了范德華力勢能預測蛋白質結構問題的數學模型,第三章中介紹了基本遺傳算法以及定義了調整策略,第四章中執行數值實驗并對結果進行分析,最后在第五章中對整篇論文做了總結并對未來的研究做了展望。
1 數學模型
范德華力是分子間作用力,是由分子(原子)間相互接近造成的極化耦合引起的。范德華力勢能可由Lennard-Jones勢能函數如下表示:

對于蛋白質結構折疊問題,給出一個氨基酸序列,它被抽象為一個C原子鏈,氨基酸之間通過范德華力相互作用。本文中,只考慮基于范德華力的蛋白質結構折疊。我們知道范德華力產生的勢能越大,蛋白質結構就越緊湊,也即最大范德華勢能對應的結構是最優蛋白質構象。
為了能找到穩定的蛋白質結構,基于范德華勢能的蛋白質結構預測問題將會轉化為數學問題。因為相鄰的兩個氨基酸之間的距離不是零,所以任意兩個原子之間的范德華力勢能可由L-J勢能方程計算得出。于是,本問題的數學模型按如下表示:

化為標準形式:

氨基酸序列被抽象為C原子鏈,查閱文獻[12]得知εi=0.12 kcal/mol,rmin= 0.21nm,同時,我們規定在鏈上相鄰的兩個氨基酸之間的距離rij=0.52 nm。
模型中約束條件意味著任意兩個氨基酸之間的距離不是零,也即任何兩個氨基酸不會處于同一個位置并且只有一個氨基酸能占有該位置。現在,一個生物問題轉化成了數學優化問題,并且范德華力勢能拋棄了HP模型的局限性,能夠更真實的反映出蛋白質的空間結構。
2 遺傳算法
遺傳算法(Genetic Algorithm , GA)最初是由美國的Holland教授提出的模擬自然界中生物進化機制的一種算法,它把達爾文進化論和孟德爾遺傳學說作為基礎,仿照生物的進化與遺傳過程,遵循適者生存和優勝劣汰的規則,通過復制、交叉和變異等一系列操作,將需要解決的問題從初始解逐代逼近最優解。
2.1 調整算子
氨基酸序列經過交叉、變異操作后,后代可能會出現循環狀態,即相同的位置同時被兩個氨基酸占據。為了克服這個缺點,我們構造了調整算子。
由于對氨基酸序列的編碼代表了方向,所以先根據初始點與編碼將每一個氨基酸的坐標確定下來,接著從序列中第一個氨基酸開始檢驗,若遇到序列中重復的氨基酸,則從當前重復的氨基酸開始,向后調整直到最后一個點的無重復坐標確定。
在進行調整操作的過程中,可能會碰到一個點的所有方向都不可以取的情況,在數值實驗時,就要定義一個記憶函數,每一個氨基酸都會對應一個集合,這個集合記錄了這個氨基酸除了當前方向還可以改變的其它方向。如果有一個氨基酸所有方向都會造成重疊,就要返回上一個氨基酸,當前方向不可行,改變上一個氨基酸的方向,并且改變對應的集合。同時,其它方向也不是隨意選取的,選取時是存在優先級的。由于和初始點距離越近,氨基酸的序列就會更緊致,所以首先取其它所有可行方向中,對應坐標和初始點的距離最近的方向,最后得到不會發生重疊的序列。
2.2 改進遺傳算法的步驟
對于預測蛋白質結構的優化問題,改進的遺傳算法按照如下步驟進行:
Step1隨機編碼產生初始種群。本文編碼方式為:將“沿x軸正方向”設置為1,“與x軸正方向成120°”設置為2,“與x軸正方向成240°”設置為3。種群中隨機設置五個個體(氨基酸序列),檢驗每個氨基酸序列的有效性,如果是不合理序列,就要通過調整算子把它變為合理的序列,計算每個序列的適應度,規定適應度為每個序列的范德華勢能。
Step2選擇。采用輪盤賭選擇,進行交叉的個體被選擇的概率與它的范德華勢能成正比,進行變異的個體被選擇的概率與它的范德華勢能成反比:
在本文中,每次循環選擇三個準備進行交叉的個體,選擇兩個準備進行變異的序列,于是,交叉如果能夠進行就會產生六個新個體,變異能夠進行則會產生兩個新個體。
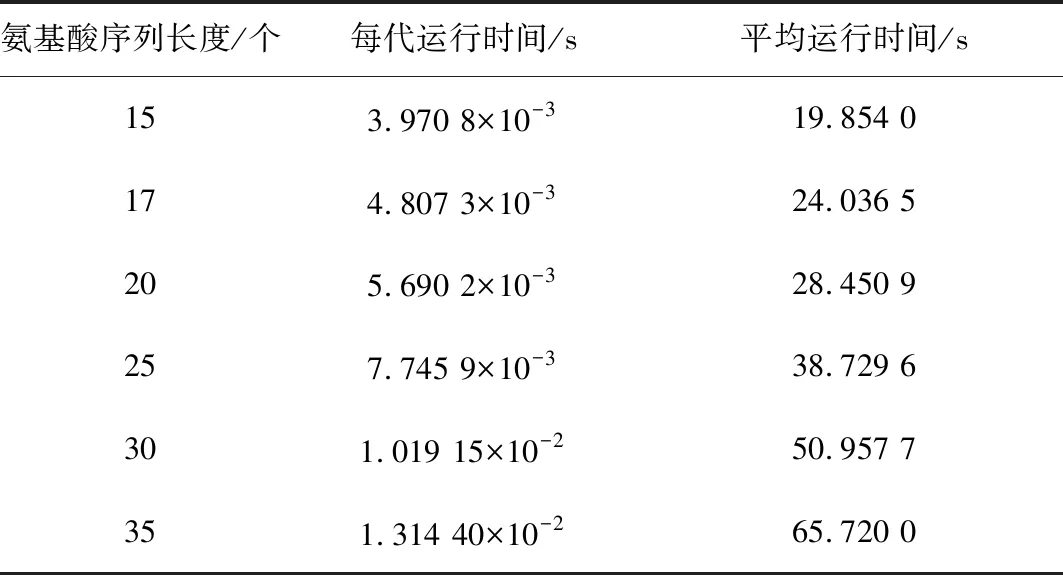
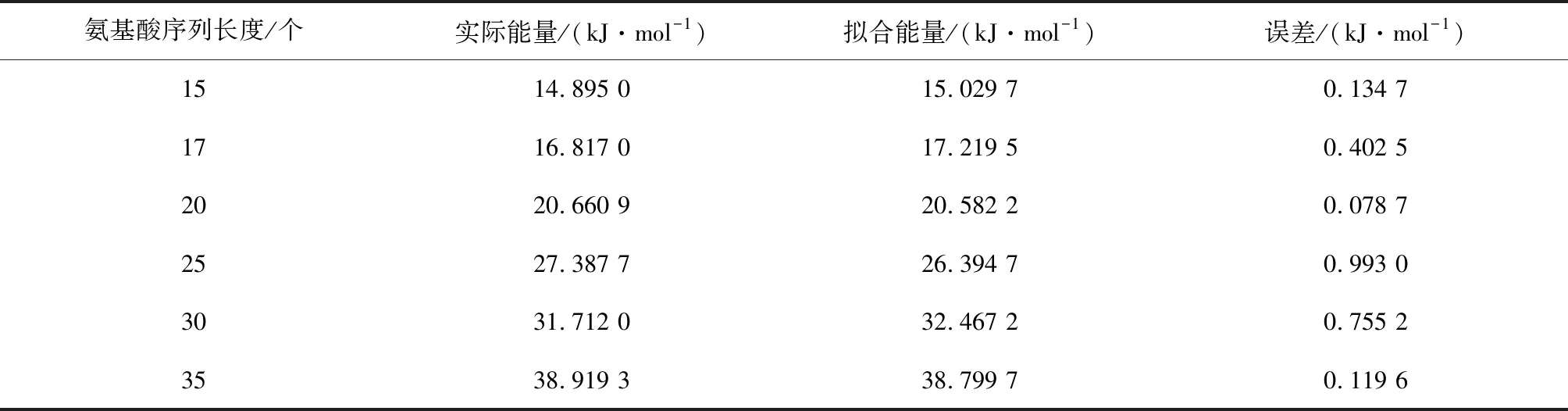
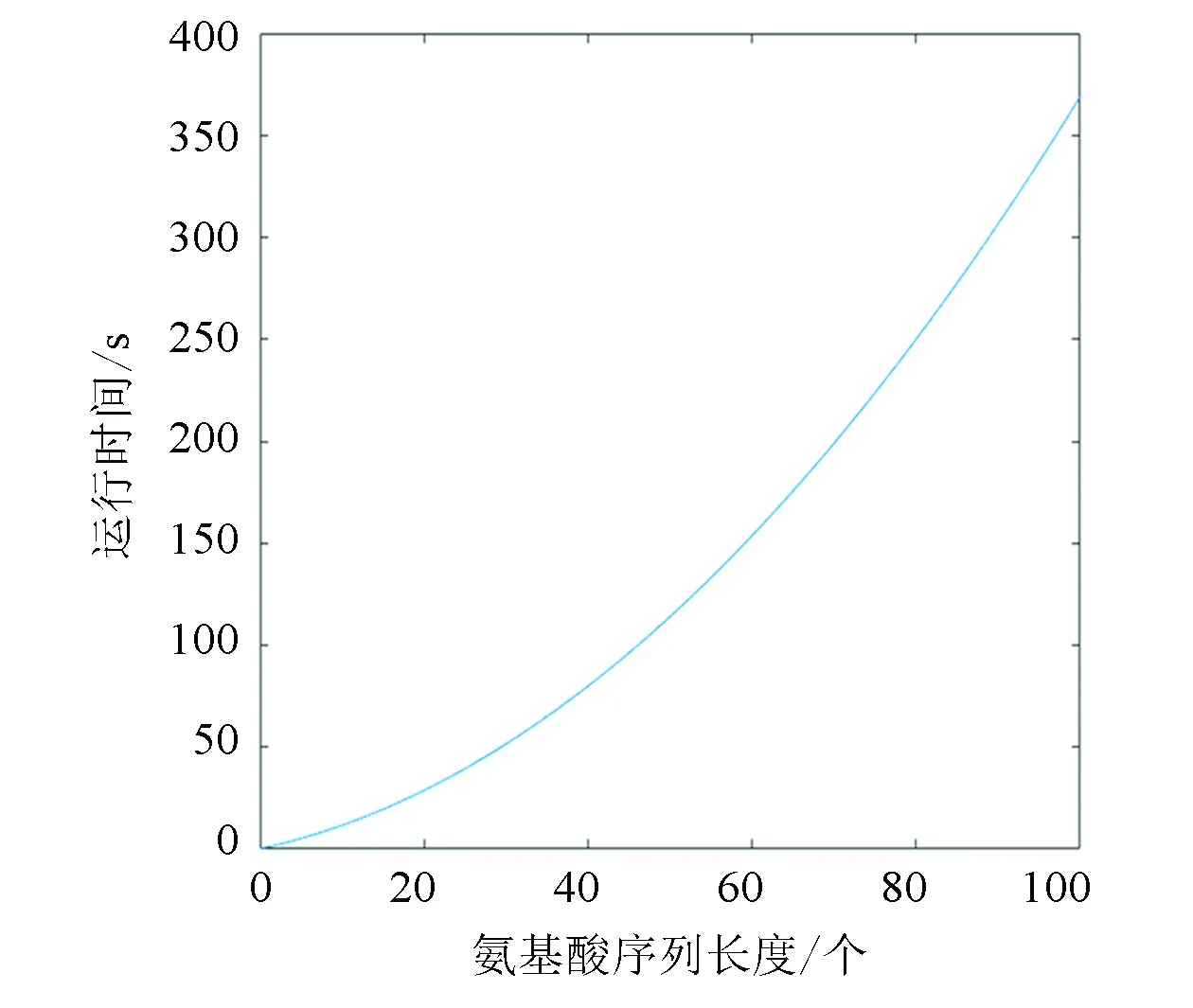
Step3交叉。采用單點交叉,確定交叉概率pc=0.8,之后產生一個隨機概率r,且0 Step4變異。采用均勻變異,設置變異概率pm=0.05,之后產生一個隨機概率,如果隨機概率小于變異概率,則執行變異操作,即對被選擇進行變異的兩個個體,隨機一個變異位點,只改變這一個位點的編碼,變異規則按照如下方式:1→2,2→3,3→1,生成兩個新個體。和交叉操作一樣,為了防止新生成的個體不符合規則,也要對新生成的個體進行檢驗,不合理則調用調整算子,合理則繼續。 Step5適應度評價。一次循環下來,通常都會產生新個體,計算新產生個體的范德華力勢能。 Step6種群更新。將新生成的個體的適應度與父代進行比較,如果子代個體中有個體的適應度大于父代的適應度,保存子代的最優個體,淘汰父代中差的個體,總之要始終保持種群中有五個個體,在迭代過程中不斷更新種群。 Step7重復步驟 Step 1~Step 6,一直循環到5 000代,最后得到最優解。 由于在遺傳算法的過程中,可能會出現局部最優解的情況出現,所以為了克服這個缺陷,在進行數值實驗的過程中要重復進行五次以上的實驗取最優解。 為了驗證模型和改進算法的有效性,進行數值實驗,分別預測氨基酸序列長度為15,17,20,25,30,35的蛋白質結構。 在進行數值實驗時,對于不同長度的氨基酸序列,我們都重復預測了五次,比較得出一個范德華勢能最大的構象,結果見圖1所示。 進行數值實驗時,累加五次實驗所得構象的范德華勢能,求出平均勢能,同時記錄不同長度序列計算每代的運行時間以及得到最優解時平均運行時間,結果分別如表1和表2所示。 從表1中可以看出,平均勢能與最大范德華勢能的誤差比較小,完全在可接受的范圍內,這也反映出改進后的遺傳算法的有效性。觀察表1和表2中的數據,我們推測:(1)序列越長,運行時間會越長。(2)范德華勢能隨著序列長度的增加而增大。(3)應用本文的方法,可以在可接受的時間里得到較長的序列的構象。(4)蛋白質的構象越緊致,結構會更穩定。 通過觀察表1中范德華勢能與序列長度的數據,擬合得出能量與序列長度的關系函數及其函數圖像(見圖2): y=0.0052x2+0.9285x-0.0678 其中,x表示氨基酸序列長度,y表示對應的范德華勢能。 分別用擬合函數和改進遺傳算法計算了表1中序列的最大范德華勢能,比較結果如表3所示: 圖1 不同長度的氨基酸序列的二維拆疊構象 表1 不同長度序列對應的范德華勢能Table 1 Van der Waals potential energy corresponding to sequences of different lengths 表2 不同長度序列對應的運行時間Table 2 Running time corresponding tosequences of different lengths 圖2 能量與長度的關系Fig.2 Relationship between energy and length 氨基酸序列長度/個實際能量/(kJ·mol-1)擬合能量/(kJ·mol-1)誤差/(kJ·mol-1)1514.895 015.029 70.134 71716.817 017.219 50.402 52020.660 920.582 20.078 72527.387 726.394 70.993 03031.712 032.467 20.755 23538.919 338.799 70.119 6 從表3的誤差來看,擬合的效果非常接近程序的結果,這說明擬合函數是可以接受的。于是我們采用擬合函數分別預測序列長度為500,1 000和2 000的氨基酸序列的最大范德華勢能,結果見表4。 表4 能量擬合函數的預測結果Table 4 Prediction results of energy fitting function 從表4中獲知,當氨基酸序列長度是500時,最大范德華力勢能是1764.2 kJ·mol-1;當序列長度是1 000時,最大范德華勢能是6128.4 kJ·mol-1;當序列長度是2 000時,最大范德華勢能是22 657 kJ·mol-1。我們發現,隨著氨基酸序列變長,其最大范德華勢能也會增大,證實了之前的猜測。 我們通過觀察表2中程序總運行時間和序列長度的數據,可以擬合得出運行時間和序列長度的函數及其函數圖像(見圖3): y=0.0282x2+0.8656x+0.2150 其中,x表示序列長度,y表示總運行時間。 圖3 運行時間與長度關系Fig.3 Relationship between running time and length 分別用擬合函數和改進遺傳算法計算了長度為20和30的序列的運行時間,比較結果如表5。 從表5的誤差和誤差率來看,擬合的效果非常接近程序的結果,這說明擬合函數是可以接受的,于是我們采用該擬合函數預測序列長度為500,1 000和2 000的氨基酸序列的平均運行時間,結果見表6。 當序列長度是500時,平均運行時間大約是2.1 h;當序列長度是1 000時,平均運行時間是 8.1 h;當序列長度是2 000時,平均運行時間是31.8 h。此結果說明基于范德華勢能預測蛋白質結構是可行的。 表6 時間擬合函數的預測結果Table 6 Prediction results of time fitting function 通過對實驗數據的分析可以看到,基于范德華勢能的數學模型,通過改進的遺傳算法來預測蛋白質的空間結構具有很大的可行性,最后得到的氨基酸序列的構象是很緊湊的,因此是比較符合真實結構的。 本文討論了基于范德華力的蛋白質結構預測問題。選擇范德華勢能作為數學優化模型,變量是任意兩個 C 原子之間的距離。目標函數要求范德華勢能最大,約束條件是兩個氨基酸不占據同一個位置。選擇遺傳算法來解決此數學模型,并且對遺傳算法做了改進。為了防止氨基酸的位置重疊,引入了調整算子的概念,使氨基酸序列最大程度的符合其真實的生物學特性。在數值實驗中,改進的遺傳算法搜索能力和搜索效率都得到了提高,證明了模型和算法的可行性和有效性。 在未來有很多方向可以追求。首先,本文研究的是二維平面上蛋白質結構預測問題,而真實的蛋白質結構是三維的,在以后的研究中可以考慮將模型和改進的算法擴展到空間蛋白質預測問題中去。其次,可以將模擬的結果與真實的蛋白質結構進行比較,檢測模型和算法的有效性。第三,還可以比較蛋白質結構預測的疏水親水模型和范德華勢能模型的結果,分析出各自的優缺點。 總而言之,本文的模型和方法為蛋白質結構預測問題提供了相當大的潛力。3 數值模擬
3.1 實驗結果
3.2 最大范德華勢能擬合函數及誤差分析
Fig.1 Amino acid sequences with different lengths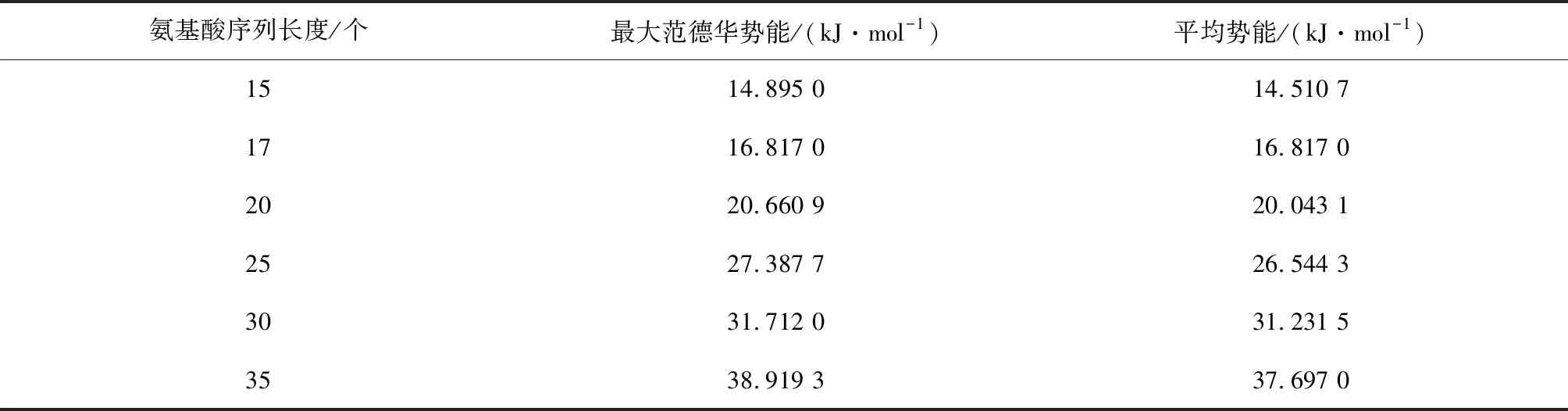


3.3 時間與長度擬合函數及誤差分析

4 總結與展望

