三維編織碳/酚醛復合材料高溫熱響應的數值計算

張 拜,李旭東

（蘭州理工大學 省部共建有色金屬先進加工與再利用國家重點實驗室，蘭州 730050）

熱防護系統（thermal protection system，TPS）是用來保護空間飛行器在高溫環(huán)境中免遭燒毀或過熱的結構和材料。碳/酚醛復合材料作為理想的熱防護材料，具有耐高溫、耐燒蝕、抗沖擊等特點，被廣泛地應用于航空航天領域[1-2]，如飛行器頭部、固體火箭發(fā)動機噴管、返回艙防熱罩等。隨著航空航天技術的快速發(fā)展，飛行器部件服役環(huán)境更加苛刻，開發(fā)新型碳/酚醛熱防護材料尤為重要。在這類熱防護材料的研制過程中，準確預測高溫條件下防熱材料的熱響應行為，尤其三維溫度場的演變規(guī)律，可以為熱防護系統的設計和優(yōu)化、解決防熱過度冗余或不足提供有效的參考和依據。

為了準確預測碳/酚醛復合材料的熱響應行為，首先要考慮溫升過程中防熱材料內部發(fā)生的物理化學變化[3]。在加熱過程中，酚醛基體與碳纖維最大的不同是前者發(fā)生了熱分解反應而后者沒有。酚醛樹脂高溫熱解后，會在基體表面形成多孔炭層并釋放出熱解氣體。一方面，多孔炭層隨著溫度的升高和加熱時間的延長而變厚，并且充當隔熱層進而保護內部結構，熱解氣體在炭層內的流動、換熱等過程會對整個材料的溫度場分布產生重要影響；另一方面，由于基體熱解以及熱解氣體溢出材料表面，導致酚醛基體的密度發(fā)生衰減，產生質量損失。而與之相比較，碳纖維則始終保持恒定的材料密度，質量并未發(fā)生損失。在分析碳/酚醛復合材料熱解炭化的基礎上，很多學者已經對其高溫條件下的熱響應行為進行了大量的研究。Helber等[4]關注于表面炭層的消耗，將熱解氣體產物、外界環(huán)境、炭消耗率聯系在一起，耦合求解了熱力平衡條件下的表面能量和質量守恒方程。Paglia等[5]和Dec等[6]建立了簡單的二維有限元模型，計算了加熱條件下，碳/酚醛復合材料的溫度場分布以及材料表面的形貌變化。與之相類似，易法軍等[7]應用簡化模型的方法，將三維材料結構轉化為二維數值計算模型，預測了恒定熱流邊界下碳/酚醛復合材料的應力場和溫度場分布規(guī)律。朱燕偉等[8]建立了碳/酚醛復合材料的整體模型，考慮了材料的炭化和熱解氣體的流動對能量方程的影響，計算了冷壁熱流作用下防熱材料的溫度、氣體壓力、熱解率等隨時間和位置的變化過程。除此之外，文獻[9～10]還針對高溫環(huán)境中熱解炭化型復合材料的物理化學變化過程建立了數學模型，這些模型基于材料內部的傳熱傳質過程，求解了材料內部的瞬態(tài)溫度場等變化情況。

分析現有的工作可以發(fā)現，目前對防熱材料熱響應的數值計算較多地采用了簡化模型，這些模型將復雜的三維問題通過化簡降維變?yōu)榭汕蠼獾暮唵螁栴}，從而極大地方便了數值計算。然而，應用簡化模型預測的溫度與實際情況出入較大[3,11-12]；并且，隨著防熱復合材料的發(fā)展，編織型復合材料在熱防護系統中的應用越來越廣泛，而一維或二維模型擬實性差,已經不能完全反映三維編織復合材料的真實情況；此外，文獻中對三維編織碳/酚醛復合材料高溫熱響應的計算報道較少。基于此，本工作對基體和纖維束分開建模，利用能量和質量守恒方程，考慮熱解過程中酚醛基體密度和材料熱屬性的變化，對三維編織碳/酚醛復合材料的高溫熱響應行為進行數值計算，預測復合材料瞬態(tài)溫度場以及熱解度的分布規(guī)律，研究質量損失率和炭層厚度的變化情況。

1 內部熱響應計算

高溫條件下，碳/酚醛防熱復合材料的基體和纖維具有不同的行為特征。酚醛基體隨著溫度的升高發(fā)生熱分解反應，材料被炭化，并且密度和熱屬性也隨著熱解過程的進行而不斷地變化；而碳纖維則相對穩(wěn)定，其密度和材料熱屬性均可視為恒定的常數。

1.1 熱傳導

在未發(fā)生熱解反應時，材料內部的溫度場由熱傳導方程計算：

1.2 基體熱解

在加熱過程中，酚醛基體的熱響應涉及溫度場、物性場、化學反應，是一個高度耦合的非線性過程。熱解反應可表示為[13]：酚醛樹脂→炭殘余物（炭層） + 熱解氣體。

本工作在計算酚醛基體的熱響應行為時，作了如下的簡化和假設[14-15]：

（1）將酚醛基體處理為各向同性材料，因而各方向的材料熱屬性相同。

（2）熱解氣體與固體殘余物間不發(fā)生化學反應，且兩者保持熱平衡。

基于以上假設，加熱條件下酚醛基體的能量和質量守恒方程分別為[14-16]：

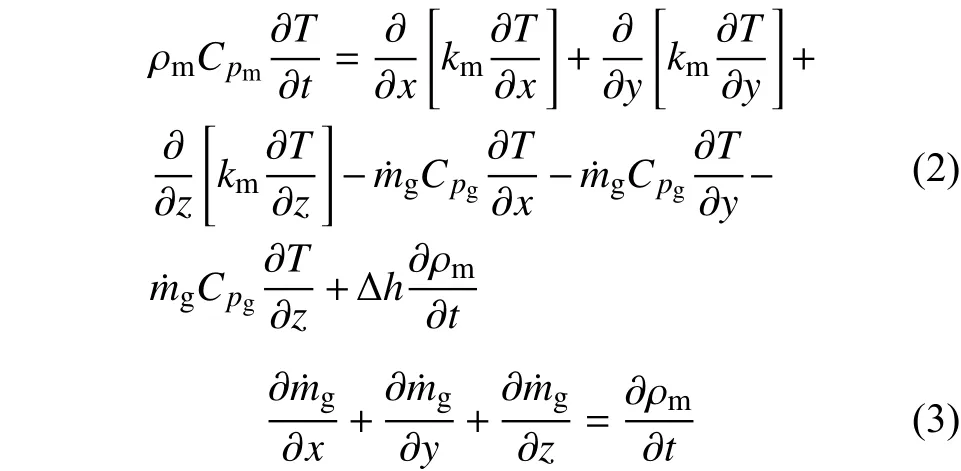
酚醛基體的熱解反應速率應用Arrhenius動力學反應方程計算[15-16]：

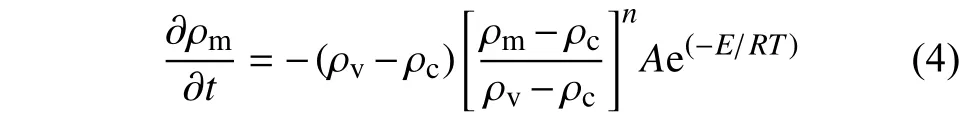
2 基體熱屬性和加熱面熱流

在加熱過程中，酚醛基體的傳熱是一個變物性的傳熱過程。開始時熱屬性為酚醛樹脂的材料屬性，而在加熱到一定程度后基體完全被炭化，材料熱屬性變?yōu)槎嗫滋繉拥膶傩浴Ｔ谟嬎氵^程中，為了獲得中間狀態(tài)的材料性能參數，假設此狀態(tài)的材料屬性與加熱過程中原始酚醛材料和完全炭化材料的相對質量分數有關，這一質量分數定義為[14-16]：

則中間狀態(tài)基體的導熱系數、比熱容分別為[14-16]：

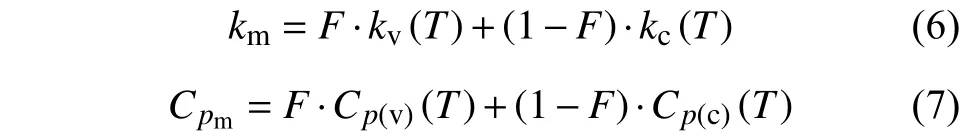
在恒定熱流加熱并考慮熱解氣體溢出表面帶走熱量的情況下，加熱面的熱流關系用下式計算：

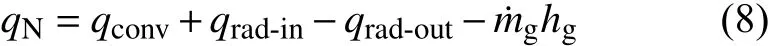
3 多尺度模型和纖維束材料屬性

3.1 多尺度模型

在對碳/酚醛復合材料熱響應行為的計算過程中，建立兩種不同尺度的模型，如圖1所示。對于宏觀尺度模型，增強體為纖維束，其直徑為0.27 mm，模型的長度和寬度均為12.5 mm，厚度為10 mm；纖維束由碳纖維編織而成，碳纖維直徑d為7 μm；假設碳纖維在纖維束中呈直線均勻分布并且相互平行[17]，則細觀尺度模型作為代表性體積單元（representative volume element，RVE）包含碳纖維和酚醛基體，其可由單根纖維、4根1/4纖維部分以及基體組成，該模型的長度 a為 8.2 μm，寬度 b為 13.9 μm，高度h為12.5 mm；細觀尺度模型用來計算加熱過程中細觀RVE的材料屬性值，該屬性作為纖維束的材料屬性應用于熱傳導方程，并結合基體熱解方程最終實現對宏觀材料結構熱響應行為的計算。

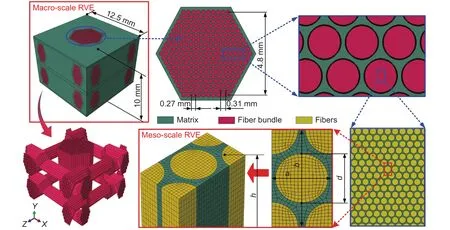
圖1 碳/酚醛復合材料的幾何模型Fig.1 Geometry model of carbon/phenolic composite

3.2 纖維束材料屬性

加熱過程中由于酚醛樹脂的不斷熱解，基體的導熱系數、比熱、密度在材料內呈不均勻分布且其值隨溫度的變化而變化。因此，在應用細觀尺度模型計算纖維束的材料屬性參數時，對基體的材料屬性取其平均值，而碳纖維由于未發(fā)生熱解反應，其材料屬性處理為常數。纖維束整體的屬性參數由基體和碳纖維的屬性參數加權得到，其導熱系數或密度的計算式為[18]：

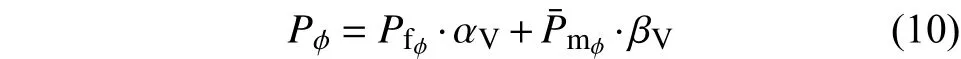
纖維束的比熱計算式為[17]：

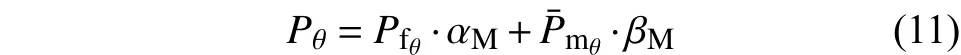
在細觀尺度模型中，碳纖維所占的體積分數可用下式計算：

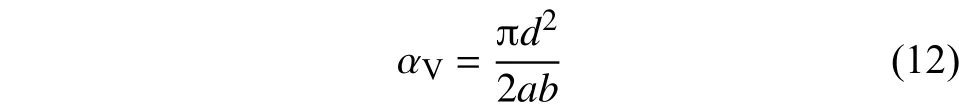
則基體所占的體積分數為[18]：

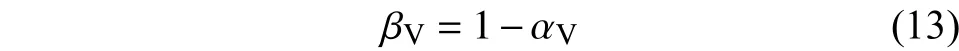
碳纖維所占的質量分數計算式為：

則基體所占的質量分數為：

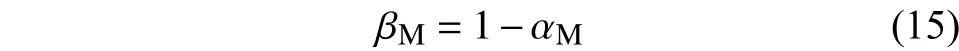
4 計算結果及分析

基于以上數理方程并借助于有限元軟件COMSOL Multiphysics，對一種三維編織碳/酚醛復合材料在單側熱流加熱下的熱響應行為進行計算。計算過程中建立兩種不同尺度的模型，其中，細觀尺度模型采用了結構化網格，網格分布如圖1所示；由于宏觀尺度模型的結構相對復雜，對其采用四面體網格剖分并且單元增長率設置為1.2，獲得的網格分布如圖2所示。對于兩種不同尺度的模型，均指定：材料結構的頂面（y = 10 mm）為加熱面（heating surface），施加在此面上的邊界條件應用方程（8）計算，加熱熱流qconv為405 kW/m2；頂面和底面對環(huán)境輻射的發(fā)射率分別為0.9和0.05；除頂面和底面外，剩余各側面定義為絕熱壁面。由于外界環(huán)境輻射進入材料的熱量較小，因此計算中忽略了qrad-in對溫度場的影響。計算過程中，使用的材料屬性和熱解反應的動力學參數分別如表1、表2所示，炭層的導熱系數如圖3所示。

4.1 纖維束

圖4為加熱過程中纖維束的導熱系數和比熱隨溫度的變化曲線，圖5為其密度隨溫度的變化曲線。從圖4和圖5可以看出，在加熱開始時各屬性參數的變化較為平緩，當溫度達到一定程度時各曲線由平緩過渡到劇烈變化。其中，導熱系數隨溫度的升高而單調增加，這主要是因為加熱過程中酚醛樹脂熱解炭化產生了炭層，炭層的導熱能力比酚醛樹脂的強（導熱系數如圖3所示），使得基體整體的導熱能力增強，最終導致纖維束整體的導熱能力也隨之增強，表現為導熱系數逐漸變大。

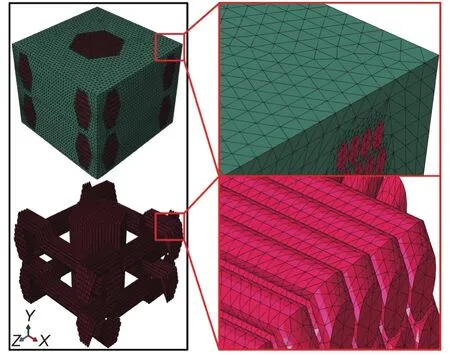
圖2 宏觀材料結構的網格剖分Fig.2 Mesh of macro material structure

表1 材料屬性Table 1 Material properties

表2 熱解反應動力學參數Table 2 Chemical kinetic parameters

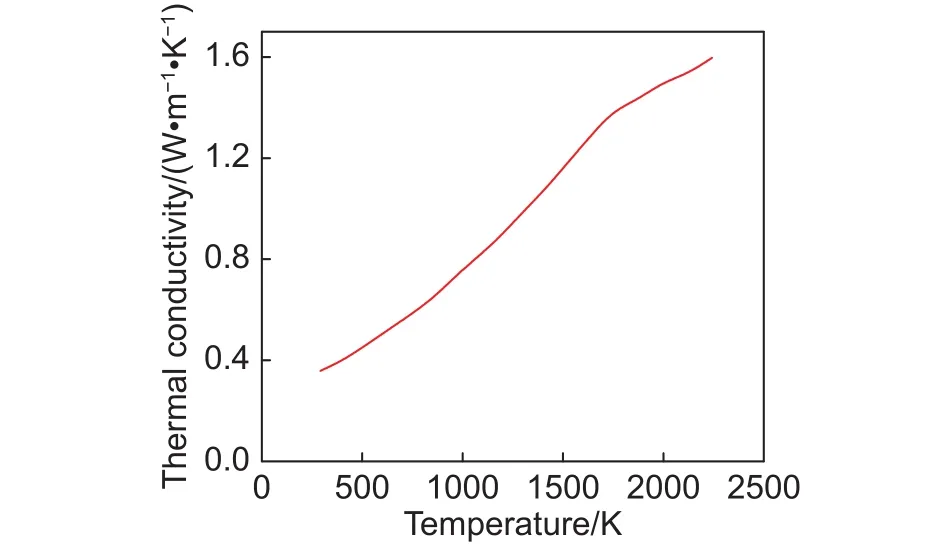
圖3 炭層的導熱系數Fig.3 Thermal conductivity of char layer

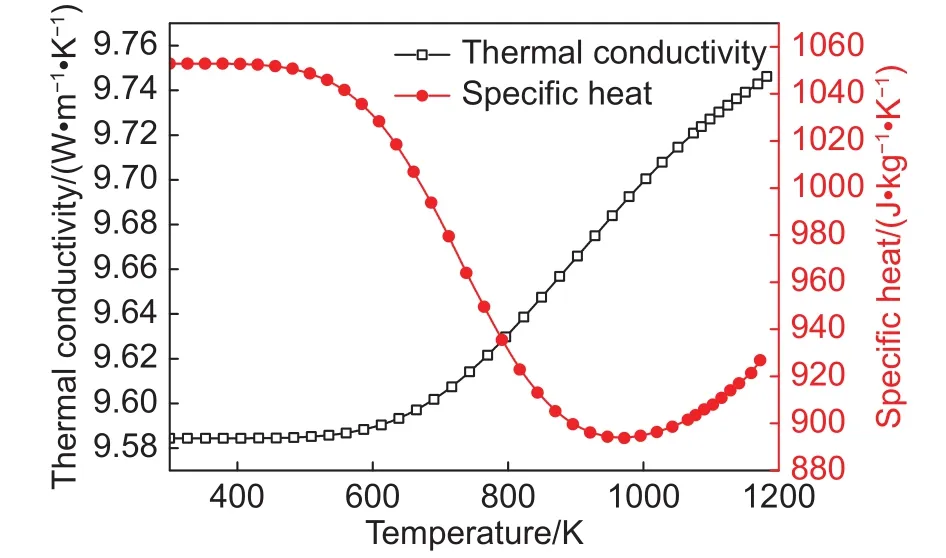
圖4 纖維束的導熱系數和比熱隨溫度的變化Fig.4 Thermal conductivity and specific heat of fiber bundle as a function of temperature

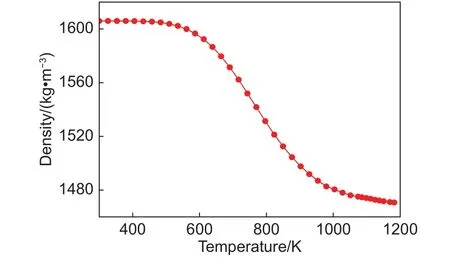
圖5 纖維束的密度隨溫度的變化Fig.5 Density of fiber bundle as a function of temperature

另外還可以看出，導熱系數升高的幅度并不大，整個加熱過程中導熱系數僅在0.17的范圍內變動；與導熱系數的變化趨勢正好相反，密度隨溫度的升高呈單調遞減，這是由于酚醛基體熱解后產生的炭層密度較低，使得基體整體的密度出現衰減，從而導致了纖維束整體的密度出現遞減的趨勢；比熱隨溫度的升高先減小后出現了小幅度的增加。產生這種變化趨勢的原因為炭層的比熱隨溫度的增加而增加，其變化規(guī)律在表1中給出。在一定的溫度范圍內，炭層的含量以及比熱均處于相對較低的水平，此時的炭層不足以使基體整體的比熱升高，基體整體的比熱在此溫度范圍內逐漸較小，因而使得纖維束整體的比熱隨之減小；當溫度繼續(xù)升高，炭層含量以及比熱隨之增加。在溫度達到一定數值時，此時的炭層含量和比熱足以使基體整體的比熱升高，基體整體的比熱在此溫度后開始逐漸增加，因而導致了纖維束整體的比熱出現小幅度的升高。

4.2 復合材料整體

圖6為加熱過程中碳/酚醛復合材料整體和纖束維的溫度場分布。由圖6可以看出，隨著時間的增加復合材料的溫度隨之升高，在頂面達到最大值1420 K，并且在材料的厚度方向上溫度由頂而底逐漸降低，在30 s時上下面最大溫差達到了1118 K。溫升過程中，復合材料的溫度場分布并不均勻，具有很大的溫度梯度，這是由于復合材料的基體和纖維為異質體，兩者的導熱能力存在明顯的差異。碳纖維的導熱系數比酚醛基體的大，熱量可以傳遞到更深的位置，因此出現了材料內部豎向纖維束的溫度比基體的溫度要高；而對于酚醛基體，其在加熱過程中產生了表面炭層，該炭層導熱系數小而比熱較大，當在外界加熱時炭層吸收了大量的熱量從而對內部結構起到隔熱作用，這樣就形成了熱量集中在材料的表層區(qū)域而較難傳遞到材料內部，因此出現了表層區(qū)域的溫度比其他區(qū)域的溫度要高。

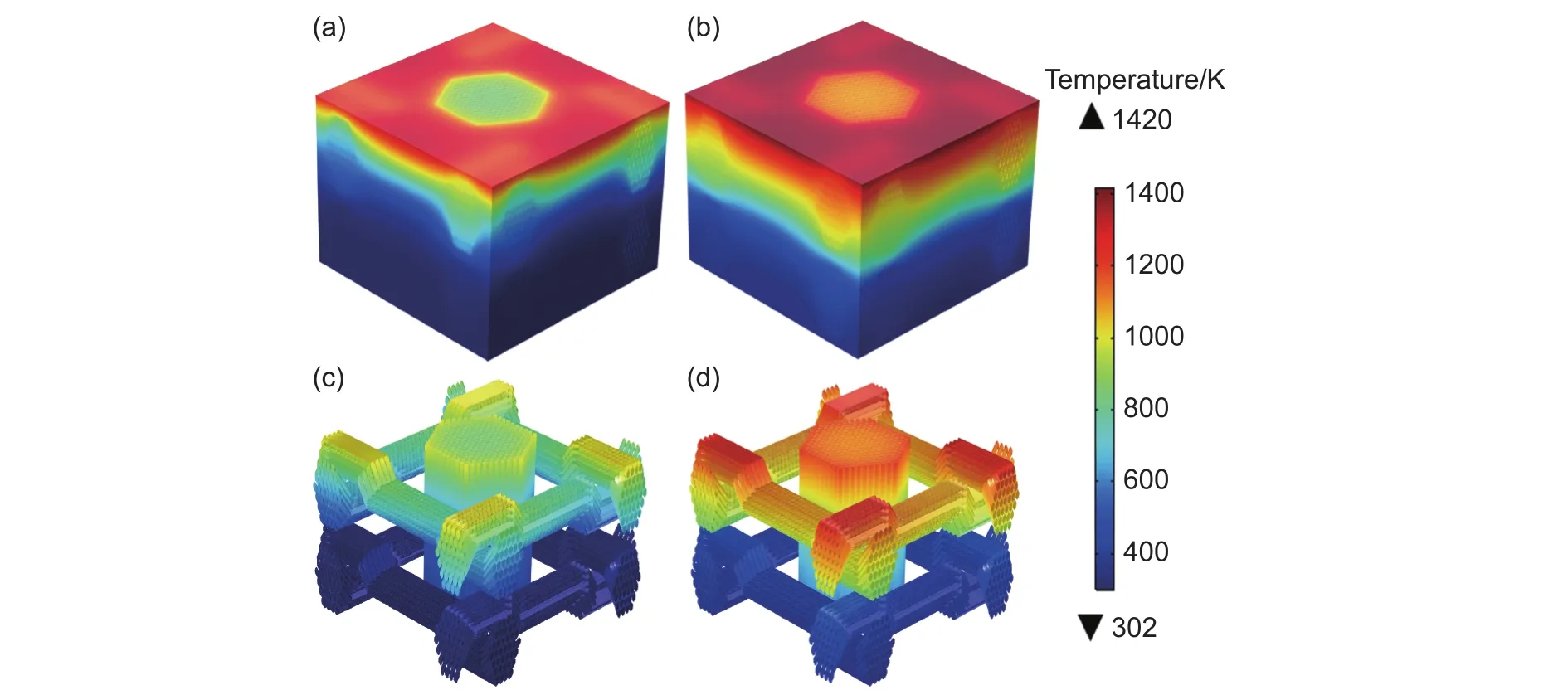
圖6 碳/酚醛復合材料的溫度分布 （a）整體 15 s；（b）整體 30 s；（c）纖維束 15 s；（d）纖維束 30 sFig.6 Temperature distributions of carbon/phenolic composite （a）whole 15 s；（b）whole 30 s；（c）fiber bundle 15 s；（d）fiber bundle 30 s

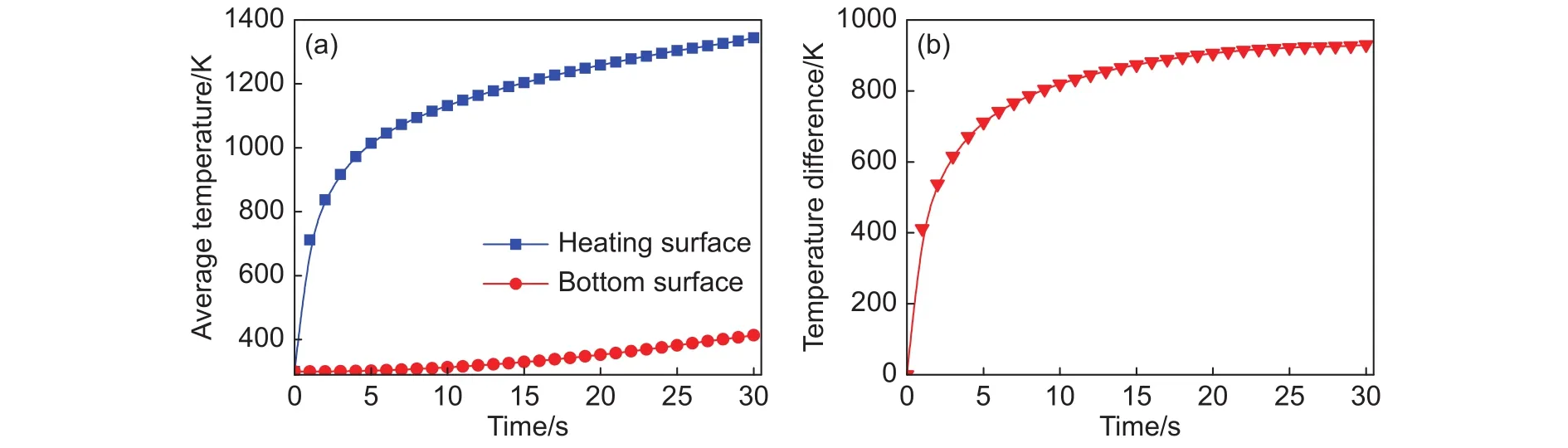
圖7 復合材料面溫度和溫差隨時間的變化（a）面溫度-時間；（b）溫度差-時間Fig.7 Surface temperature and temperature difference of composites as a function of time（ a） surface temperature vs time；（b） temperature difference vs time

圖7 為頂面和底面的平均面溫度和兩者之間的溫差隨時間的變化曲線。由圖7可知，在加熱開始時，加熱面的平均溫度隨時間的增加而迅速升高，在第 5 s時平均溫度達到了 1014.3 K，而在這5 s的時間段內溫度的增加值為714.3 K；隨著時間的延長，加熱面平均溫度的溫升速率逐漸降低，在第 30 s時平均溫度達到了 1343.4 K，而在這 25 s的時間段內溫度增加值為329.1 K，僅為5 s時間段內溫度增加值的46%。這是因為，在加熱開始時加熱面溫度較低，表面材料還沒有進行充分的熱解，由熱解氣體帶走的熱量和表面對環(huán)境的輻射熱量均較小，因此在外界熱流作用下加熱面獲得較多的熱量，使得溫度在短期內迅速升高；而在一段時間后，加熱面溫度達到一定數值，表面材料充分熱解，由熱解氣體帶走的熱量和表面輻射損失的熱量增加，因此加熱面獲得的熱量減小，溫升速率逐漸降低，最終加熱面溫度在外界熱流、表面輻射散熱、熱解氣體溢出帶走熱量的共同作用下將趨于平衡。材料底面的平均溫度變化較為緩慢，在第30 s時溫度值僅為412 K；加熱面和底面的平均溫度差隨時間的變化與加熱面平均溫度的變化具有相似的規(guī)律，隨著時間的增加平均溫差保持在931K的溫度范圍內。

加熱過程中最大溫度和平均溫度分別代表了復合材料產生的溫度極值和材料整體的溫度水平，圖8為碳/酚醛復合材料的最大溫度和平均溫度隨時間的變化曲線。由圖8可以看出，復合材料整體的平均溫度隨加熱時間的增加幾乎呈線性變化。在30 s時，平均溫度達到了743 K，而最大溫度則達到1420 K，是平均溫度的1.91倍；溫度的最大值出現在加熱面上，30 s時加熱面的平均溫度為 1343.4 K（見圖 7），比此時刻的溫度最大值小了76.6 K。

加熱過程中，由于酚醛樹脂的不斷熱解，基體密度出現衰減并產生了炭層，材料質量隨著加熱時間的延長而出現虧損。圖9為碳/酚醛復合材料質量損失率隨基體平均溫度的變化曲線。由圖9可以看出，質量損失率隨基體平均溫度的升高而迅速增加，在溫度達到500 K后，復合材料的質量損失率幾乎呈線性變化，在30 s時質量損失率達到了15.93%，可見加熱過程中碳/酚醛復合材料出現了明顯的質量損失。

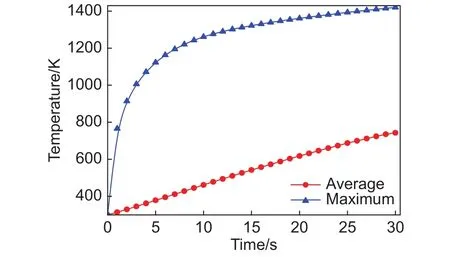
圖8 碳/酚醛復合材料的最大溫度和平均溫度隨時間的變化Fig.8 Maximum temperature and average temperature of carbon/phenolic composite as a function of time

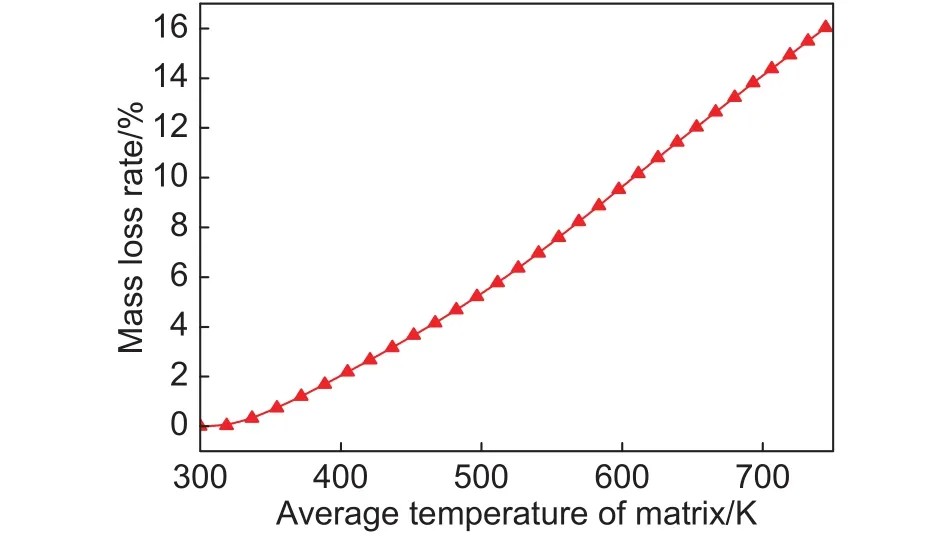
圖9 質量損失率隨基體平均溫度的變化Fig.9 Mass loss rate as a function of average temperature of matrix

熱解度反映了加熱過程中基體材料熱分解反應的強弱程度，其數值在0到1之間。0表示材料完全熱解，1表示材料還未進行熱解。圖10為酚醛基體的熱解度分布，由圖10可知，加熱過程中頂面溫度較高材料首先發(fā)生熱解，隨著時間的推移，材料表面完全熱解形成炭化層，并且熱解層隨著溫度的傳遞而逐漸向厚度方向轉移。除此外，還可以看出，酚醛基體的熱解層實際上僅發(fā)生在一個很薄的區(qū)域內，材料的大部分區(qū)域由未熱解（熱解度為1或者接近于1）和熱解完成（熱解度為0或者接近于0）的材料所占據。

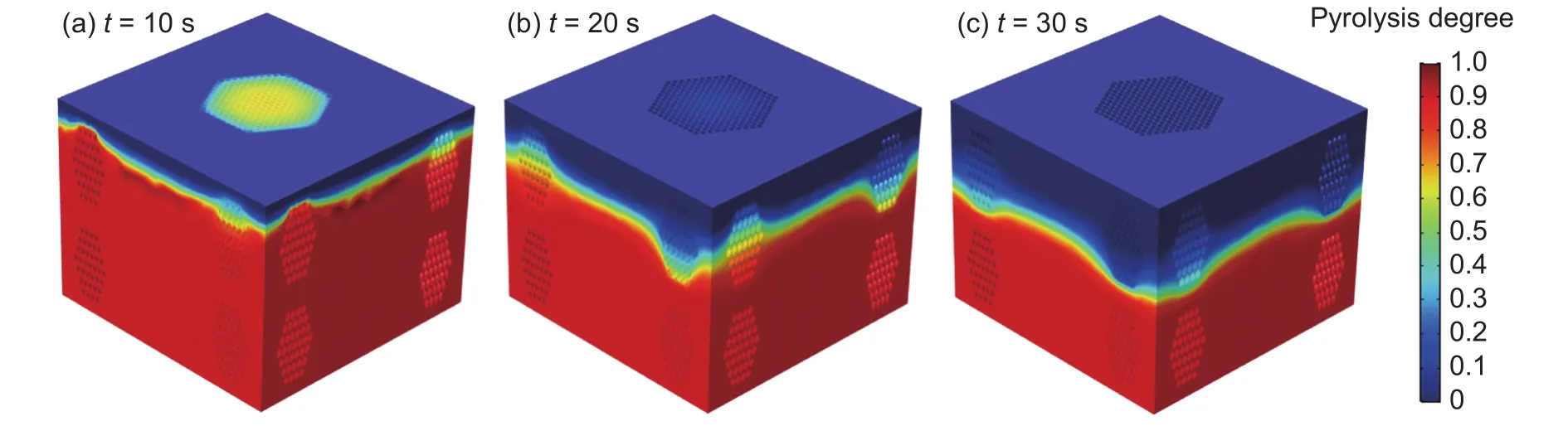
圖10 酚醛基體的熱解度分布Fig.10 Pyrolysis degree distributions of phenolic matrix （a）10 s，（b）20 s，（c）30 s

隨著酚醛樹脂的高溫熱解，材料被炭化產生表面炭層。一方面，該炭層的產生可以起到輻射散熱的作用；另一方面，炭層還可以充當高溫隔熱層，對內部材料起到保護作用。因此，炭層的產生情況也是評價熱防護材料防熱性能的重要指標之一。圖11為加熱過程中炭層的生成位置。可以看出，炭層主要出現在頂端加熱面附近區(qū)域，這是因為加熱面上溫度高，材料熱解充分成炭率高。隨著加熱時間的延長，炭層厚度增加且向材料結構的厚度方向延伸。

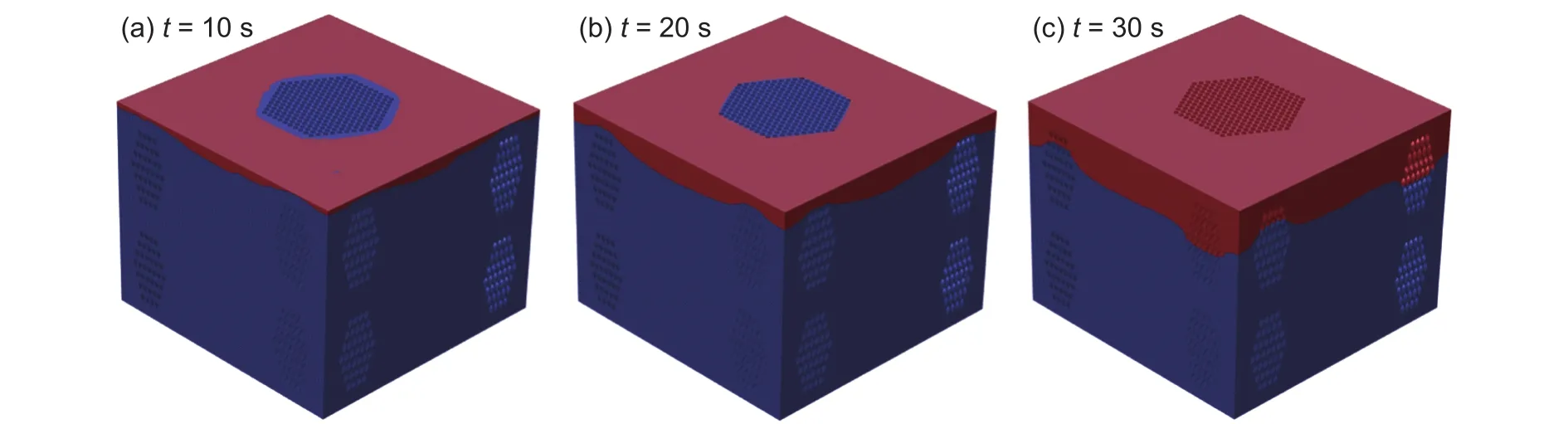
圖11 炭層的生成位置Fig.11 Formation position of char layer during heating process （a）10 s，（b）20 s，（c）30 s

圖12 為平均炭層厚度隨時間的變化曲線，由圖12可以看出，炭層的產生需要一段時間的過渡，在此時間段內炭層厚度為0。這主要是由于，加熱開始時表層基體材料出現熱解，當熱解度達到一定數值時才開始生成炭層，而要達到這一熱解度需要一個很短的過渡時間。在此時間段后隨著時間的繼續(xù)增加炭層厚度迅速增加，在30 s時酚醛基體的平均炭層厚度達到了1.288 mm。

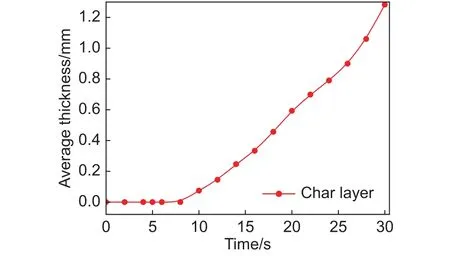
圖12 平均炭層厚度隨時間的變化Fig.12 Average thickness of char layer as a function of time

5 結論

（1）加熱過程中，三維編織碳/酚醛復合材料具有不均勻的溫度場分布。在加熱面上基體和纖維束之間存在較大的溫差，在30 s時這一溫差達到了310 K，并且此時最大溫度為1420 K。在材料內部，豎向纖維束的溫度比基體的溫度要高。

（2）加熱過程中，酚醛基體發(fā)生熱解炭化，材料密度衰減，質量出現虧損。在基體平均溫度達到一定數值后（約為500 K），酚醛基體的質量損失率幾乎呈線性增加，表明隨著溫度的升高材料將出現較大的質量損失。基體炭層的產生需要一段時間的過渡，在這一時間段內炭層平均厚度為0。