基于LSTM的共享單車需求預測

李穎宏 馬 勇

（北方工業大學城市道路交通智能控制技術北京市重點實驗室，北京 100043）

隨著綠色出行和環保觀念的深入人心，共享單車自推出以來不僅深受用戶喜愛，也減輕了城市路網壓力和擁堵情況，方便了“最后一公里”的出行。共享單車進入城市的一年多時間里，發展速度極快。隨著使用單車的用戶增多，共享單車企業投放車輛數量也是與日俱增。然而，一味地增大投放量，在增強城市交通服務能力方面并未成正比性，反而帶來了一系列令人質疑的問題，其中亂停亂放、高峰期一車難求尤為嚴重，這些存在的問題如何運用高效科學的方法去解決已成為一個關于共享單車的熱門話題。

針對這些問題，國內各共享單車企業對共享單車系統的研究主要可以歸納以下幾個方面：（1）預測研究，如摩拜使用深度學習方法對供需進行預測，具體將Tensorflow框架下的卷積神經網絡應用于單車流量預測；（2）智能調度研究，如摩拜的紅包單車，通過綜合運用物聯網、云計算和大數據，對單車實現實時狀態的精確控制，發現單車“黑洞”，以貼紅包的方式，激發用戶自覺自行，讓單車離開“黑洞”，回到需要單車的地方；（3）智能站點設立的研究，如“摩拜智能推薦停車點”，該停車點可實現亞米級定位，實時掌握停車區域內單車的數量、狀態、位置及各區間的流量情況等信息，為車輛投放、調度和運維提供智能指引。

共享單車的需求預測是一個共享需求比較新的問題。陳昕昀[1]等利用BP神經網絡對公共自行車單站點調度需求量進行預測研究，發現了自行車流量隨時間分布的規律；Borgnat[3]等使用里昂自行車共享系統的歷史數據，通過組合模型來預測一天每小時的需求量；近來有很多學者將機器

學習的方法運用到預測需求量[4-5]。以上這些方法幾乎都局限于有樁式公共自行車的研究，而針對無樁式的共享單車，目前涉及成型的理論及方法并不多，并且針對有樁式公共自行車的需求預測方法往往具有局限性，不能兼顧出行的空間和非空間屬性。

本文使用一種序列化的神經網絡模型，該模型在解決梯度爆炸和梯度消失的基礎上，能夠提取共享單車出行OD序列間的依賴信息，即流量的時間變化規律，建立基于LSTM的線性回歸預測模型。其次，針對不同地域間出行的自流動性和關聯性，在提出的預測模型基礎上，將軌跡數據中挖掘的距離特征納入預測模型，以時空的角度來描述各個出行區域之間的相互影響，利用摩拜公司30多萬條單車軌跡數據，通過劃分不同的特征數據集，訓練模型，并驗證了該模型在共享單車需求預測方面的優越性。

1 LSTM算法

長短期記憶網絡（Long-Short Term Memory，LSTM），由 Sepp Hochreiter和Jürgen Schmidhuber于1997年提出的，是一種特定形式的循環神經網絡。LSTM通過增加門操作，即輸入門、遺忘門、輸出門，優化了自循環的權重，保持權重的動態變化性，在模型參數固定的情況下，在一定程度上解決了梯度消失或者梯度膨脹的問題。

1.1 LSTM模型

LSTM模型結構定義如圖1所示，它包含三個門操作，控制和保護每一個元胞的狀態。該操作既能夠丟棄低狀態數據，又能夠向狀態中加入新的數據。

圖1 LSTM原理結構圖

1.2 LSTM的向前傳播

由模型的結構圖可知，LSTM實現了三個門計算，即遺忘門、輸入門和輸出門。遺忘門處理的數據是上個樣本的短期記憶和本次樣本的輸入，通過Sigmoid函數決定保留多少上一時刻的單元狀態到當前時刻的單元狀態；輸入門決定如何將新信息和舊信息相結合，嵌入到新的狀態；輸出門決定當前時刻的單元狀態有多少輸出。每個LSTM包含了三個輸入，即上時刻的單元狀態、上時刻的LSTM的輸出和當前時刻輸入。LSTM向前傳播機制如下：

遺忘門：

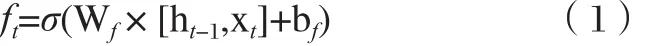
式中：[]—兩個向量相連合并；

Wf—遺忘門的權重矩陣；

σ—sigmoid函數；

bf—遺忘門的偏置項。

輸入門：

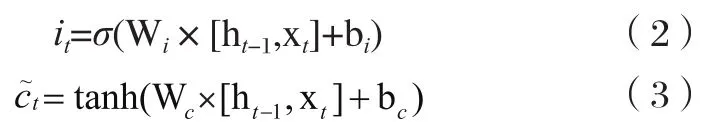
第一部分是上一步得到的過濾后的長期狀態信息，第二部分是根據上個元胞的和本元胞的輸入獲得的更新信息。當前時刻的單元狀態由遺忘門輸入和上一時刻狀態的積加上輸入門兩部分的積，即：

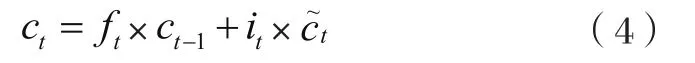
輸出門：

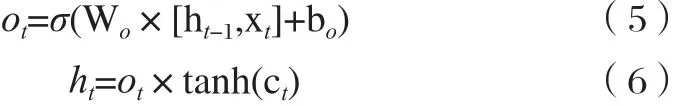
輸入結合本次和上次的短期狀態信息，獲取新的信息，再點乘長期記憶的狀態通過tanh函數正規化得到輸出。

2 預測模型的構建

共享單車作為一種短距離出行工具，在復雜的城市交通網絡中，已經成為城市“慢交通”系統的一部分。相對于機動車流量的動態特性，共享單車流量有其獨特的自流動特性，使得某些騎行區域點之間具有一定的關聯性，某一騎行域的共享單車預測需求量不僅與自身歷史時刻流量相關，而且與該區域有直接或者間接流量流動的區域相關。若預測模型僅考慮目標區域在歷史與未來時間間隔內單車流量的相關性，而忽略其相關區域的流量狀況，將不可避免地降低預測準確性。因此，建立如圖2的預測模型框架。

首先 ，將單車軌跡數據按照各區塊出行時間劃分成日內單車流量時間序列；然后利用K-means聚類算法，以與預測區域有直接或者間接流量流動為依據，進行聚類劃分，得到日內相關區塊單車流量時間序列，輸入到LSTM神經網絡模型，找出時空特性規律；最后利用線性回歸預測模型得到預測值。

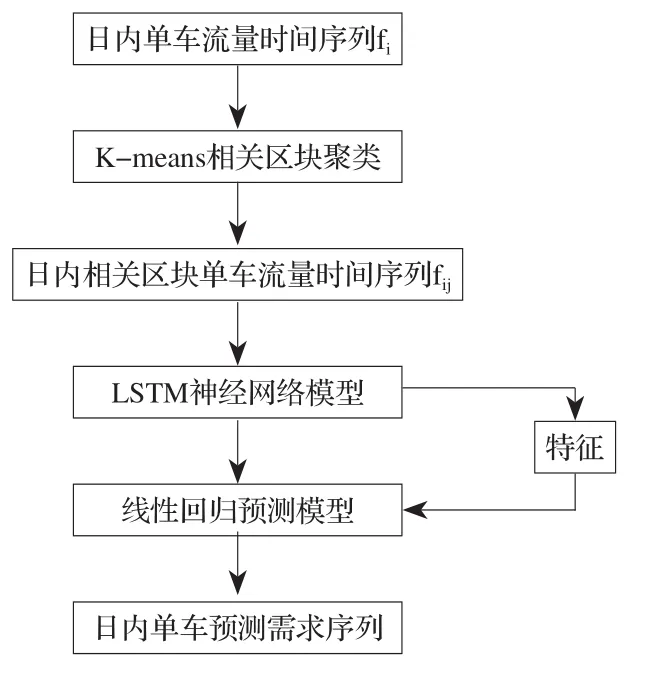
圖2 基于LSTM的預測模型圖

2.1 K-means聚類

本文所用到的部分專業術語定義如下：

n：區域數；

Si：第i個區域 ；

Sij：與i區域相關的j區域；

fSit：t時刻Si區域的單車出行需求流量；

fSijt：t時刻j區域到i區域的單車流量；

Lm：第m條歷史出行軌跡。

某一區域共享單車出行流量在受該區域位置影響的同時，也與其相關區域的單車出行規律相關。本文基于各區域歷史出行軌跡信息及出行規律，得到共享單車流量，以及本區域的單車需求量，提出了二次K-means算法，得到與預測區域直接相關的區域簇。第一次先按區域的地理位置進行聚類，得到區域簇，第二次從得到的N個區域中按軌跡信息得到與預測區域Si相關的區域S1，S2，S3，...，Sn。

K-means聚類算法如下：

輸出 ：Si：S1，S2，S3，...，Sn。

（2）初始化k=0；

（3）while k ＜ K do ；

（4）for i = 1:n do；

（6）k = k+1;

（8）for j = 1:N do；

（9）Sij包含于Lij；

（10）更新Si：S1，S2，S3，...，Sn；

（11）返回Si：S1，S2，S3，...，Sn。

2.2 LSTM神經網絡模型

LSTM在循環神經網絡RNN結構上增加了各層的門限節點：遺忘門、輸入門、輸出門。通過調節門限的打開或關閉，判斷模型各層網絡的長時間記憶狀態在該層的輸出結果是否加入當前層的計算中，從而實現模型的記憶功能。本文基于LSTM神經網絡模型的特性，對提出的線性網絡預測模型進行訓練優化，搭建三層單胞神經網絡模型如圖3所示。

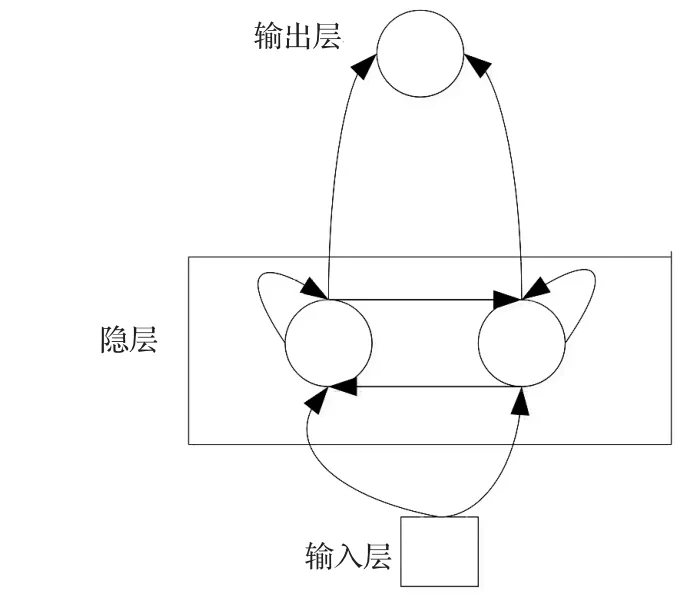
圖3 三層LSTM神經網絡模型圖

該模型的計算方式與傳統的BP神經網絡相似，結合結構圖1，根據式ot=σ(Wo×[ht-1,xt]+bo)和ht=ot×tanh(ct)可進行計算。模型的訓練步驟如下：

（1）數據樣本的準備。經過數據預處理得到的共享單車出行數據，通過K-means聚類得到關聯的出行規律樣本數據集作為模型的數據輸入。

（2）網絡參數的初始化。使用python的keras庫，完成訓練參數的調整，具體參數包括最大迭代次數、學習率、激活函數等。

（3）網絡模型的訓練。采用BPTT（back-propagation through time）訓練算法，進行梯度檢測，使用隨機梯度下降算法（SGD）更新權重，一直到滿足最小誤差函數需求為止。

（4）網絡模型的測試。訓練過程如圖4所示。

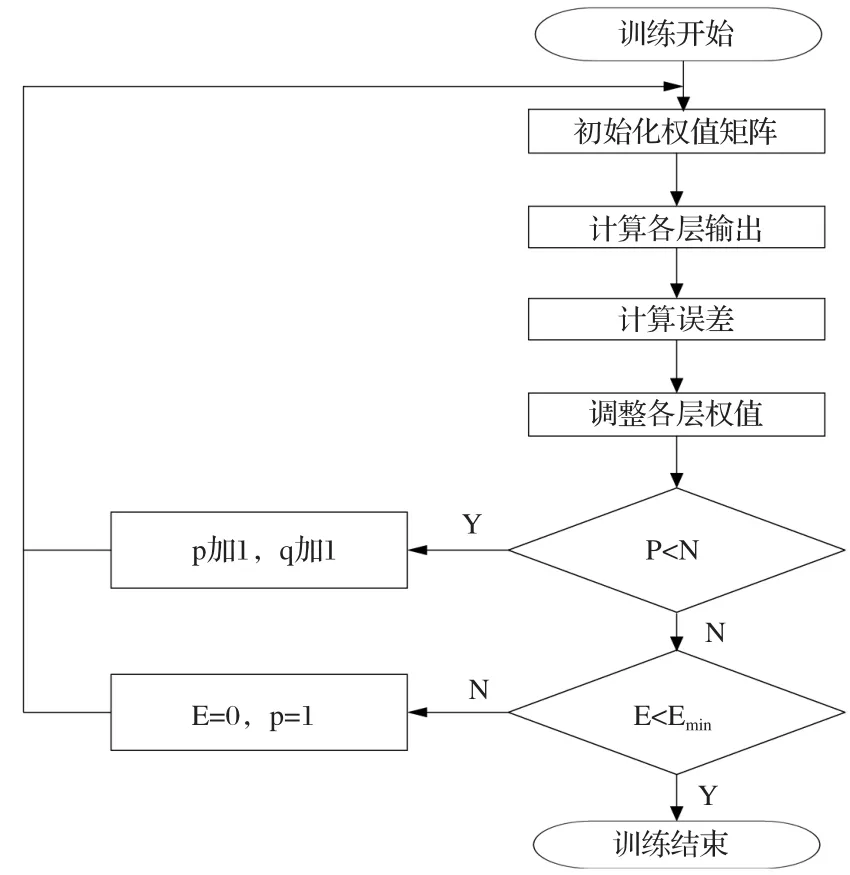
圖4 LSTM模型訓練圖

2.3 線性網絡預測模型

基于上節二次聚類得到的區域簇S1，S2，S3，...，Sn，本節將各區域點之間的復雜網絡關系簡化為一個結構圖，如圖5所示。預測區域Si，其他區域為Si的相關區域點，Vin為特定時刻相關區域Sn點到Si區域點的車流量。

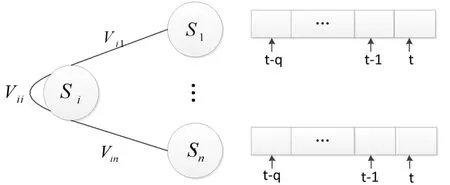
圖5 網絡模型預測結構

本研究模型是通過將特定時間間隔的車流量以及相關的權重線性組合，得到預測區域的表達式，如式（7）所示：

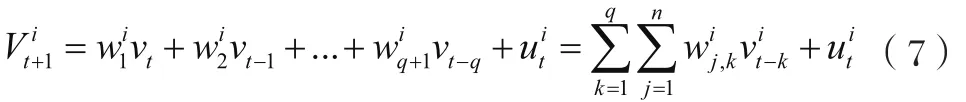
本文建立的單一線性預測網絡模型的均方根誤差都隨著預測時間間隔的增加而增加，時間間隔越長，對時間特性的學習能力越弱，不確定因素影響就越大，導致預測的均方根誤差就越大，因此，本文采用一種時間特性學習模型LSTM(Long short-term memory)對軌跡數據中隱藏的出行時間規律進行訓練學習，將長時間間隔內流量的流動特性納入預測模型中，提高預測模型的準確性與精度。

3 實驗結果與分析

3.1 數據描述

本文基于300萬摩拜共享單車用戶出行記錄數據，進行預處理后作為實驗數據驗證模型的有效性與準確性。數據是連續兩周用戶出行記錄，經過數據的規則預處理及樣本篩選，構建數據集。數據信息如表1所示。

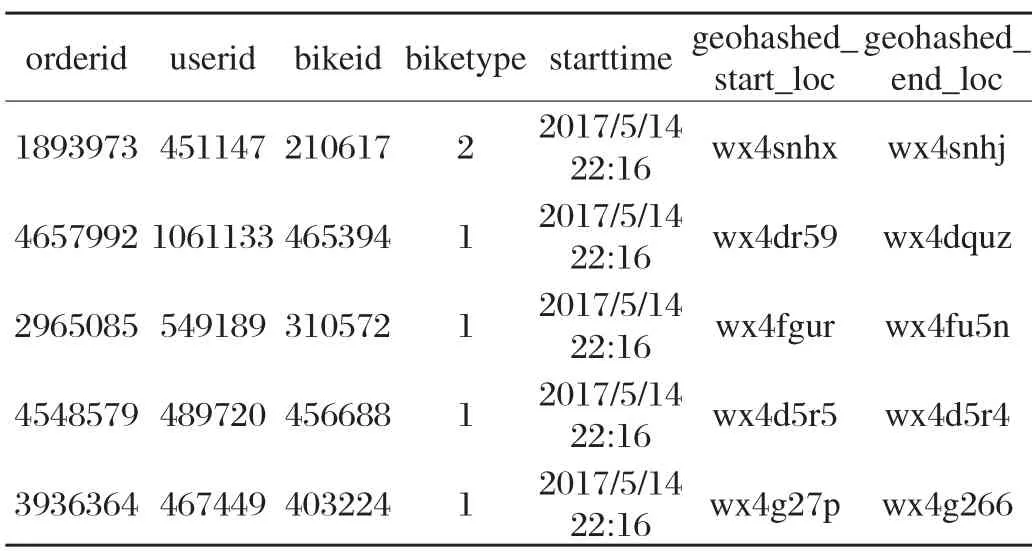
表1 用戶單車出行軌跡數據表

3.2 評價標準

本文采用均方根誤差（RMLSE）率作為評價標準來評價模型的有效性。

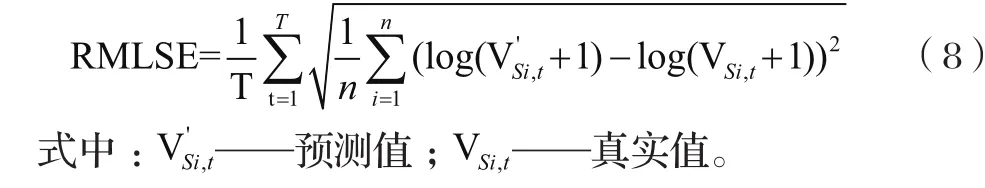
3.3 結果分析

利用綜上數據與評價指標，對預測結果與模型的有效性和準確性進行分析。

3.3.1 聚類結果分析

在本文的實驗中，使用k-means聚類對出行軌跡數據進行聚類，得到了部分出行軌跡相關簇，如圖6所示。可以看出，單車出行在一定距離之間出行的相關性。

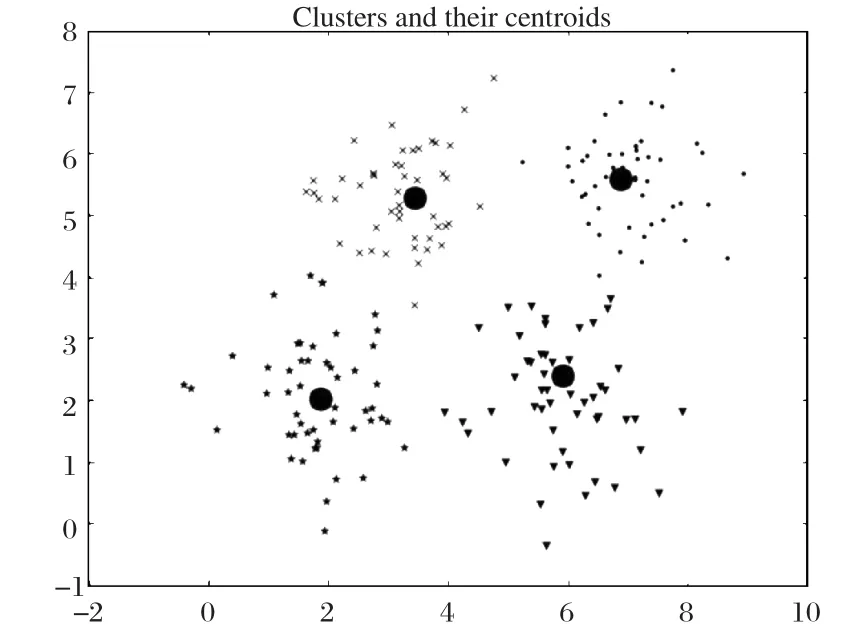
圖6 K-means聚類

3.3.2 預測結果分析

選取簇點較密集和較稀疏的區域點，圖7為兩個區域在單一網絡模型下不同時間間隔的RMLSE的變化，由圖7可知，聚類簇點越密集，相關站點越多，預測結果越準確，相反，簇點稀疏，相關站點越少，使得可依據的出行歷史數據較少，預測精度降低。無論簇點密集與否，隨著時間間隔的增加，RMLSE也呈現增加趨勢，因為不確定因素的增多，使得預測誤差也越大。

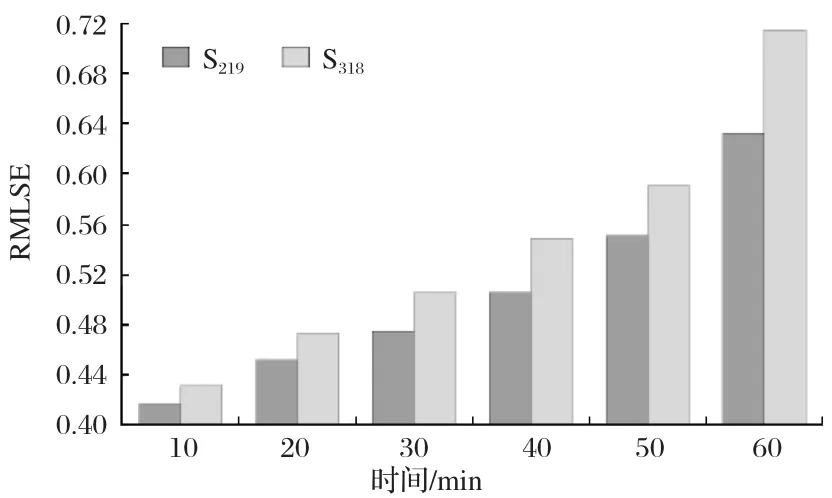
圖7 無LSTM模型下的線網絡預測誤差

圖8 為通過LSTM提取長時間數據特征之后，將長時間特性納入網絡預測模型，選取上述簇點，得到RMLSE隨時間間隔的變化規律。

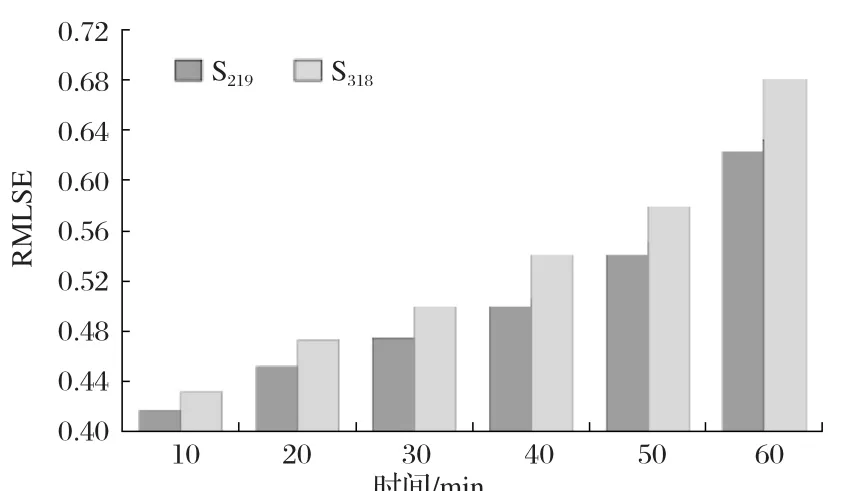
圖8 LSTM模型下的線性網絡預測誤差

由圖8可知，隨著時間間隔的增加，預測的RMLSE明顯有所下降，預測準確性得到一定的提升。

3.3.3 預測方法比較

為了驗證LSTM網絡對長時間特性的學習測特性，本文選取循環神經網RNN和支持向量機SVM進行比較，如圖9所示，本文的最終預測精度要高于其他兩種模型，并且能更快地收斂。

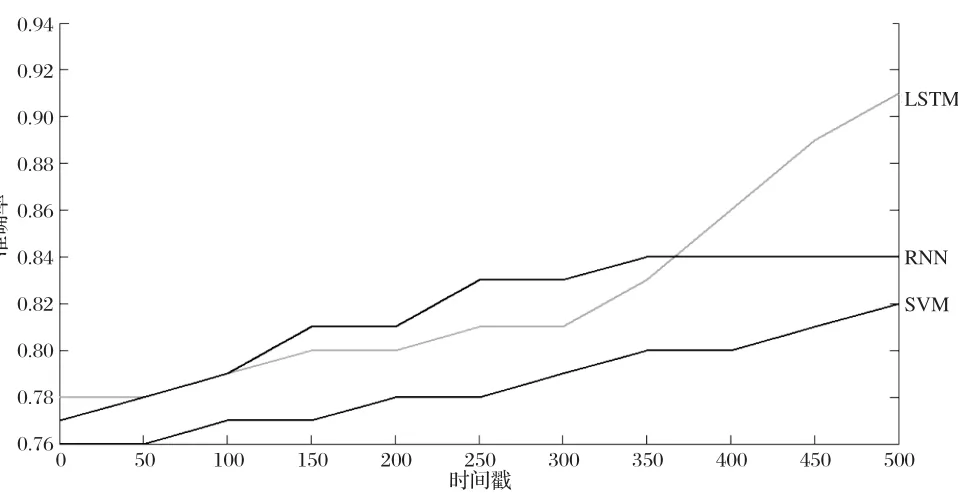
圖9 預測模型效果比較圖

4 結語

本文在已建立的網絡模型的基礎上，利用LSTM網絡對長時間間隔的歷史數據的學習特性，降低了網絡預測模型對長時間間隔數據的敏感性，提升了預測的準確性；通過與已有預測方法的比較，證實了該改進模型的實用性及有效性，并在一定程度上對預測的精度得到提升，預測誤差率僅為0.293。基于共享單車軌跡數據，對其需求的預測，未來將考慮更多因素如出行規律、工作日、天氣等來改進模型。