海上距離元胞自動機分析法

王加勝,楊 昆,朱彥輝,熊建紅

1. 云南師范大學信息學院，云南 昆明 650500； 2. 西部資源環境地理信息技術教育部工程研究中心，云南 昆明 650500

距離變換最早由Rosenfeld和Pfaltz提出，是指將每個柵格像元映射為到最近感興趣區域或目標區域的距離，其輸入圖像一般為二值圖像[1]。其中的距離一般為歐氏距離。由于根據定義計算復雜度較高，文獻[2]提出了一種距離變換的快速實現算法——楔形距離變換。該方法僅考慮鄰域像元的影響，通過兩次掃描完成距離變換。該算法速度快，但無法得到精確的結果。此后，許多學者通過改變鄰域大小和優化距離算子提高楔形距離變換精度[3-6]。

2004年，文獻[7]將距離變換引入到GIS中，討論了距離變換在GIS領域的應用場景。目前距離變換已成為GIS中的一個基本工具[8-12]。在GIS鄰域距離變換的許多應用場景中，常常需要考慮障礙區域的影響，計算非障礙柵格像元到最近目標最短路徑長度(如航線設計、海上救助等)[13-16]。這種距離變換，本文稱之為繞障歐氏距離變換。目前，未見有專門針對繞障距離變換的研究。

元胞自動機(cellular automata，CA)是一種時間和空間都離散的動力學系統[17]，廣泛應用于城市規劃[18-19]、土地利用[10]、傳染病傳播[20]、交通系統[21]、人群疏散等領域[22-24]。例如，文獻[25]構建元胞自動機模型，分析了個體行為對人群疏散效果的影響；文獻[26]將元胞自動機與系統生物學結合研究癌癥病毒的演化過程；文獻[27]集成CA與隨機森林方法模擬城市擴張過程；文獻[28]構建了城市和區域規劃元胞自動機模型。

元胞自動機的元胞與柵格數據的像元有相似之處，距離變換可以離散成為由目標像元向外擴散和更新繞障距離值的過程，因此可用元胞狀態變化來反映距離變換過程。文獻[29]提出了一種基于元胞自動機的柵格空間復雜實體加權距離變換方法，但未考慮障礙的影響。本文擬提出一種基于元胞自動機的繞障距離變換方法，并以南海及鄰近海域為例，分析該方法計算結果的精度與適用性。

1 研究區與數據

1.1 研究區

本文選擇南海及其鄰域作為研究區(0°N—24°N，98°E—122°E)，以測試方法的精度與適用性。南海及鄰域位于亞洲東南部，海域包括南海和泰國灣的全部，蘇祿海和蘇拉威西海的一部分，以及馬六甲海峽、臺灣海峽、巴士海峽等眾多海峽，是太平洋與印度洋的連接地帶。陸地涉及中國南部沿海、南海諸島、中南半島、菲律賓群島和大巽他群島。該區域島礁眾多，大小不一，陸地海岸線狹長復雜，這些特性為分析繞障歐氏距離變換結果提供了良好的測試環境。

1.2 數據及預處理

本文使用的數據資料包括陸地島礁圖層和目標點圖層。陸地島礁圖層使用中國及東南亞的行政區劃Shapefile矢量數據，通過國家地理信息公共服務平臺服務資源中全球矢量地圖服務中對南海及鄰域矢量化陸地范圍得到，比例尺為1∶1000萬，坐標系統為2000國家大地坐標系。目標點圖層通過在研究區海域隨機選取7個點，用于分組測試不同數量目標情況下繞障歐氏距離變換效果。

距離分析需在投影坐標系統下進行。在導入模型前，將數據轉換為Lambert-等角圓錐投影坐標系統，標準緯線為6°N與18°N，中央經線為110°E，單位為千米。由于距離變換結果用柵格表示，需要將投影轉換后的行政區劃圖層轉換為柵格圖層(像元大小為5 km)，1表示陸地或島礁(即障礙區)，0表示水域(正常區域)，轉換后的柵格大小為500×500。同時將目標點位置處的柵格值設置為2。處理后的柵格在此稱為元胞的環境柵格。

2 研究方法

2.1 基本概念

在介紹模型之前，有必要對文中涉及的歐氏距離、歐氏距離變換、繞障歐氏距離變換、元胞自動機等基本概念予以明確。假設二值柵格圖像尺寸為m×n，Ci(xi,yi)、Cj(xj,yj)為圖像中的任意兩像元。O為目標像元集合，B為障礙像元集合。

(1) 歐氏距離D(Ci,Cj)。用兩點坐標差值平方和的平方根表示，即

(1)

(2) 歐氏距離變換。變換的結果使得每個像元值為該像元至最近目標點的歐氏距離。設像元p的歐氏距離變換值用DT(p)表示。q為O中的任意一像元。則歐氏距離變換可由式(2)表示

DT(p)=min{D(p,q),q∈O}

(2)

(3) 繞障歐氏距離。表示任一非障礙集像元經過非障礙區到達最近目標像元最短路徑的長度。

(4) 繞障歐氏距離變換。變換結果使得任一非障礙集像元值為該像元到目標像元集的繞障歐氏距離。設Lm(p…q)表示從p經過非障礙區到q路徑的最小長度。像元p的繞障歐氏距離變換可表示為

EDT(p)=min{Lm(p…q),q∈O}

(3)

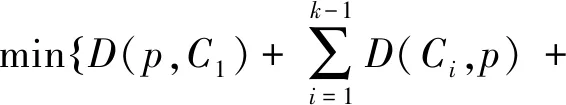
D(Ck,p)}

(4)

式中，C1,Ci,Ck?B。

(5) 元胞自動機。元胞自動機是一種時間、空間、狀態都離散，空間相互作用和時間因果關系都為局部的網格動力學模型，具有復雜系統時空演化過程的能力。每一元胞取有限的狀態、遵循同樣的規則、通過簡單的相互作用構成動態系統的演化。元胞自動機可用一個四元組描述。A={Ld,S,N,f}，其中Ld標識d維元胞空間；S為元胞有限狀態；N為鄰域元胞集合；f表示中心元胞的狀態轉換規則。

2.2 繞障歐氏距離變換CA模型

CA模型的關鍵在于元胞與狀態轉換規則的定義。在傳統的元胞自動機模型中，元胞的狀態是有限的整數。本文將元胞狀態定義為實數類型，以模擬距離變換計算過程。繞障歐氏距離變換元胞自動機模型架構如圖1所示，包括模型初始化、元胞狀態轉換、模型表達與輸出3個部分。

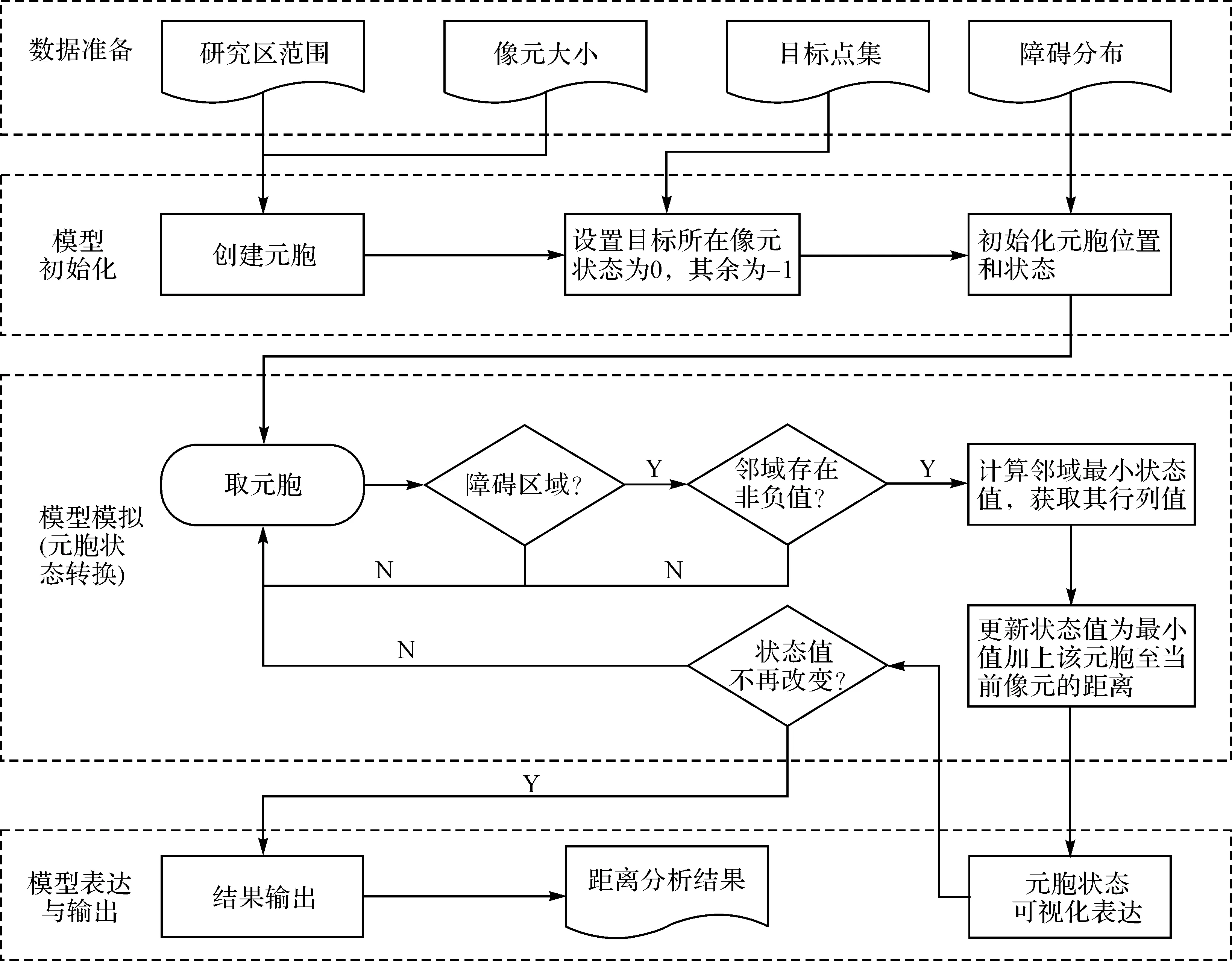
圖1 距離分析元胞自動機模型架構Fig.1 The technique route of distance analysis CA model

2.2.1 元胞定義

將研究區根據像元大小(柵格分辨率，用Sc表示)劃分為m×n正方形格網，每個單元即為一個元胞。本文將元胞的狀態定義為元胞中心位置至目標點集的繞障歐氏距離(格數)，用dt表示。此外，元胞還具有位置(即所在列x,所在行y)、狀態變化標志(fs)，障礙區標志(fl)兩個屬性。位置為(x，y)元胞表示為C(x，y)。元胞屬性的具體描述見表1。

表1 元胞屬性說明

2.2.2 模型初始化

模型初始化即模型運行前的元胞屬性初始化與參數設置。模型的參數包括環境柵格和像元大小Sc。讀入環境柵格數據后賦予元胞的障礙標志屬性fl。Sc可以根據實際要求的精度確定，影響著元胞的大小與數量；狀態dt的初始值分為兩種情況，目標點所在元胞狀態dt設為0，其余元胞為+∞(比最大距離大的數，如w×h)；狀態變化標志ft設置為0；x、y則根據元胞位置確定。元胞的屬性中fl、x、y初始化后并不會改變。

2.2.3 元胞狀態轉換

元胞狀態轉換是整個模型的核心，根據相鄰元胞的狀態，計算當前元胞的狀態。距離計算過程可以看作由目標像元向周圍逐漸擴散的過程，目標與周圍的8個像元的距離可根據歐氏距離計算得出，再加上周圍元胞的最小狀態值，即可得到元胞的狀態。本文每個時刻的元胞狀態轉換就是更新元胞距離值。狀態轉換涉及鄰域定義和轉換規則。

(1) 鄰域。本文采用鄰近的8個元胞表示當前元胞的鄰域，即元胞C(x,y)的鄰域元胞有C(x-1,y-1)、C(1,y-1)、C(x+1,y-1)、C(x-1,y)、C(x+1,y)、C(x-1,y+1)、C(x+1,y)、C(x+1,y+1)。

(2) 狀態轉換規則：

陸域元胞：不進行狀態轉換。

鄰域皆未計算的元胞：不進行狀態轉換。

其他元胞：設其與鄰域狀態(至目標最短路徑長度)組成的3×3矩陣為Dt，鄰域至中心元胞距離的3×3矩陣為A(稱為距離算子，具有中心對稱性，中心為0)。元胞下一狀態值(至目標最短路徑長度)即為矩陣Dt+A的最小元素值。這一規則轉化過程可用式(5)—式(7)表示

(5)

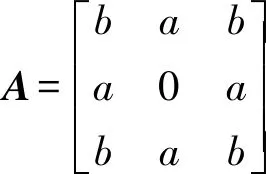
(6)

dt+1=min(Dt+A)

(7)

距離算子的選擇會影響到變換的精度和速度。在楔形距離變換中，常見的距離算子及其最大絕對錯誤率見表2。其中最小的距離算子為Butt-Maragos優化算子。本文使用該算子距離變換。

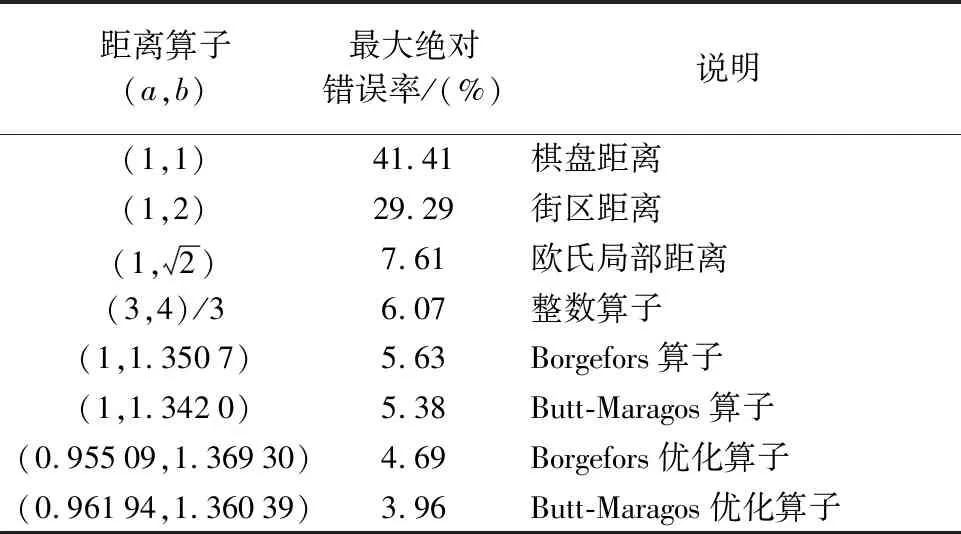
表2 常用3×3距離算子的最大絕對錯誤率[7]

注：a為算子上下左右的值；b為4個`對角的值。

2.2.4 結果表達與輸出

模型初始化后，對每一時刻t，元胞根據狀態轉換規則進行繞障歐氏距離變換和數據更新，直到所有的元胞狀態都穩定為止(對任意元胞，fs=0)，就得到模型運行結果。將結果乘以像元大小Sc即可得到該像元大小對應的繞障歐氏距離變換結果。

假設所有元胞集合為C，則模型停止的條件可表述為：對?c∈C，有dt+1=dt，則fs=0，模型停止。

元胞自動機的優勢在于能夠展示元胞演化的過程。本文應用可視化工具Processing3.0展示模型演化與距離動態計算過程。模型中可視化的內容包括海陸分布、目標位置和元胞狀態，其中最核心的是元胞的展示。海陸分布作為背景，根據柵格值將海洋和陸地分別設置為藍色與淡黃色；目標位置采用圓點表示；元胞狀態的顯示采用漸變顏色表示，涉及顏色的映射，通過運行一遍模型后獲取最大的狀態值，再進行顏色映射以獲取良好的可視效果。

模型的目的除了觀察計算過程，最重要的是結果分析。將元胞的最終狀態值按照行列號組合形成一個二維數組，根據像元大小Sc、左上角投影坐標，行列數，輸出為地理信息系統(geographical information system,GIS)軟件支持的ASCII碼格式文件，以便后期分析處理。

3 結果與討論

3.1 繞障歐氏距離變換模擬結果

將目標點數據與預處理后的環境柵格輸入模型，創建250 000個元胞組成的CA模型，采用表2最后一個算子，模擬繞障歐氏距離變換過程，結果如圖2所示。可以看出，模型動態地展現出距離變換的計算過程。計算的元胞數量圍繞目標點呈正方形向外逐漸增多，顏色也越來越深，說明元胞狀態隨著擴散更新。當兩個目標點的擴散圈相遇時(如圖2中的B位置)，接縫處(T=150的B位置)過渡自然，沒有出現橫豎形狀的突變狀態。這是由于計算過的元胞依然會根據鄰域情況作狀態更新。當擴散至障礙區域時，會繞過陸地，元胞狀態值(如圖2中的A點)反映了繞障歐氏距離。在T=240時，表示模型經過240次迭代，從目標經海域能到達的區域元胞完成距離計算，共運行了23.363 s。以上結果表明，基于CA的海上距離分析模型能夠動態展示計算過程，距離計算自動考慮到了繞障距離花費，說明模型可行。

圖2 CA模擬過程結果Fig.2 Results of CA simulation process

3.2 模擬結果與普通歐氏距離變換結果對比

為了分析模擬結果的準確度，將CA模擬結果與普通歐氏距離變換結果對比。為避免其他因素影響，只選擇1個目標點，分別對研究區作CA繞障距離變換(圖3(a))與歐氏距離變換(圖3(b))，再對兩個結果進行差值計算(圖3(c))。為直觀區分，圖3用等值區域法表示。可以看出，模擬結果與歐氏距離分析結果具有相似的空間分布特征，大部分區域數值差距在50 km以內，CA模擬結果比普通歐氏距離普遍偏高(圖3(c)中輻條之外的區域)。但在局部區域存在較明顯差異，如圖3中的A、B、C3個位置，普通歐氏距離變換由于不考慮障礙導致誤差偏大，而本文方法顧及到了這一點。這些區域二者差距在300 km以上，差距最大的出現在馬六甲海峽(圖3中的C位置)。

另外，比較結果中還存在一些低于-50 km的負值，這是由于這些位置在研究區內被障礙隔開，而無法繞障到達目標點，CA模型中未參與計算(值為-1)而歐氏距離變換結果存在值所造成的。綜上，基于CA的距離分析方法在海上距離計算上存在很大的優勢，合理考慮了繞陸地距離和無法到達的區域。

3.3 基于CA的繞障距離變換結果誤差分析

本文中的模型如果不考慮障礙分布，運算結果便可與歐氏距離變換結果對比，分析本文方法的誤差。在不考慮障礙分布情況下，普通歐氏距離變換結果即為真值。這時，設CA模擬結果為Ra，真值為Rb，則誤差E可由式(4)表示

E=(Ra-Rb)/Ra

(8)

據此計算得到的模擬結果、真值和誤差分布如圖4所示。從圖4(a)與圖4(b)對比可以看出，本文模擬結果等值線呈現出正八邊形的特征，這是由于鄰域考慮的是8鄰域所導致的。而真值是呈圓型分布，這成為了誤差的主要來源。從圖4(c)可看到誤差的分布具有傘狀特征。正八邊形邊的中點(即米字形表示的方向)處誤差為0，其余位置誤差則與其與目標連線與8個方向最小夾角有關，夾角越大則誤差也越大。從誤差統計結果可以看出CA距離分析方法的誤差范圍為0～3.96%。

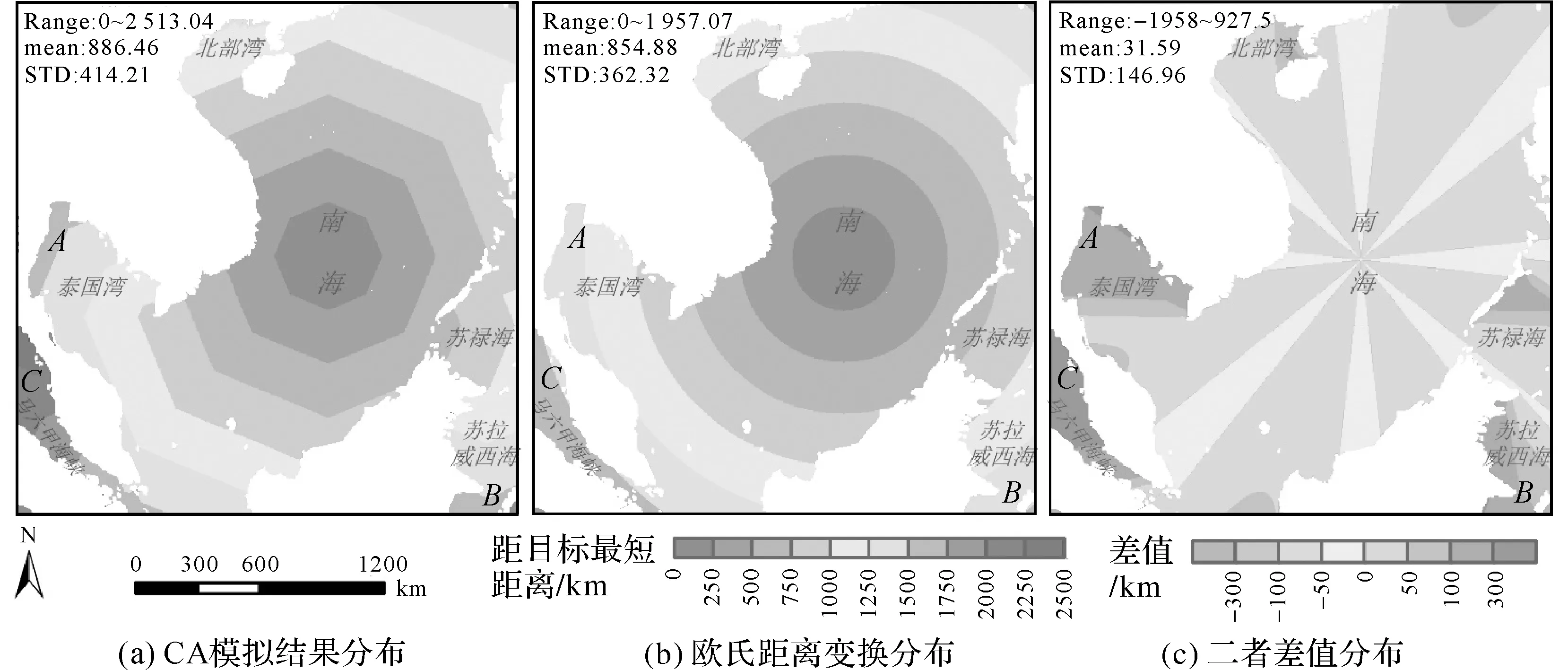
圖3 模擬結果與歐氏距離分析結果對比Fig.3 Comparison results of CA simulation and Euclidean distance transformation

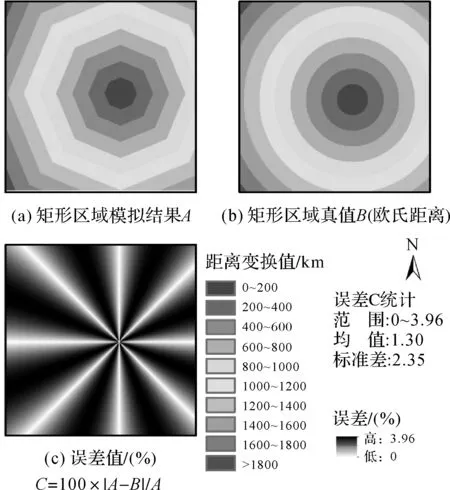
圖4 距離分析CA模型誤差分析Fig.4 Error analysis of CA based distance analysis

在有障礙的情況下，繞障距離變換值為到目標最短路徑的長度Lp，可以轉化為多條線段的長度和。即

(9)

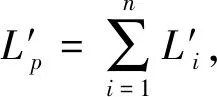
(10)

因此，本文提出的繞障歐氏距離變換的最大誤差率也為3.96%。

3.4 元胞大小和轉換規則對結果的影響

3.4.1 元胞大小對繞障距離變換結果的影響

本文元胞大小與地理信息系統中柵格的像元大小相對應。由研究方法描述可知，本文方法并不受元胞大小的限制，任意元胞大小都可以使用。但元胞大小對結果運算速度和計算精度有影響。

從運算速度來看，對特定的研究區域，元胞越大，則該區域元胞數量越少，運算速度越快；元胞越小，則該區域劃分后的元胞數量越多，運算速度越慢。

從計算精度來看，最終的繞障歐氏距離變換結果等于元胞自動機模型模擬結果乘以元胞大小(分辨率)。因此，計算精度可由式(11)計算

ε=min(a,b)×Sc

(11)

式中，ε表示計算精度；a為距離算子上下左右位置的值；b為距離算子4角的值；Sc為元胞大小。

在式(11)中，距離算子的值相對固定，因此計算精度與元胞大小成正比。元胞越大，精度值越大，精度越低。元胞越小，精度值越小，精度越高。例如本文試驗中：a=0.961 94，b=1.360 39，Sc=5 km，因此計算精度為4.809 7 km。

運算速度和計算精度相互制約，在具體應用中，像元大小的設置需在運算速度和計算精度中權衡選擇。

3.4.2 轉換規則對繞障距離變換結果的影響

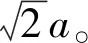
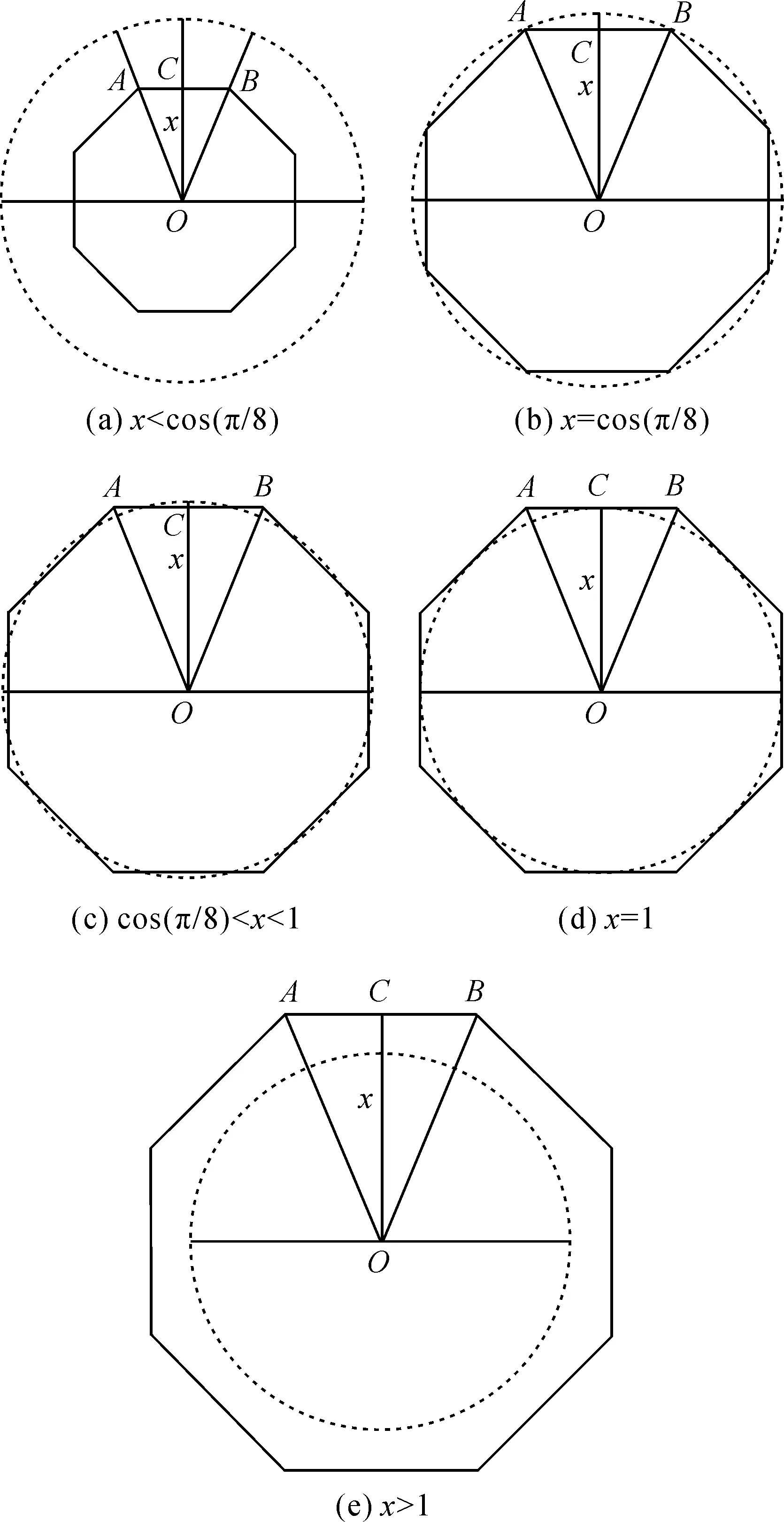
圖5 距離算子對最大絕對錯誤率影響示意圖Fig.5 The influence of distance to maximum absolute error ratio

(1) 當x

(2) 當x=cos(π/8)時，圓O為八邊形的外接圓，最大絕對錯誤率體現在O與邊垂直方向。

(3) 當cos(π/8)

(4) 當x=1時，圓O為八邊形的內切圓，最大絕對錯誤率體現在O與頂點連線方向。

(5) 當x>1時，圓O在八邊形的內部，最大絕對錯誤率體現在O與頂點連線方向。

通過幾何分析得出最大絕對錯誤率y與x的關系如下

(12)

進一步簡化為

(13)

從以上公式可看出，當0[1+cos(π/8)]/2時，y=f(x)為遞增函數。當x=[1+cos(π/8)]/2≈0.961 94時，得到y的最小值[1-cos(π/8)]/[1+cos(π/8)]≈0.396=3.96%。該取值即為本文使用的Butt-Maragos優化算子。為此，本方法轉換規則的最優算子為Butt-Maragos優化算子，結果誤差≤3.96%。

4 結論與展望

本文以南海為例，基于海陸分布數據(障礙分布)和目標點數據，提出了一種基于CA的繞障歐氏距離變換模型，模擬后得到變換結果，并對其繞障效果和精度進行分析。本文得到以下結論：①CA為繞障距離變換提供了一種解決方案，直觀動態地展示繞障歐氏距離變換的計算過程，是一種計算可視化的實現方式；②CA繞障距離變換模型在運行中能夠自動更新，兩目標的距離擴散接縫處過渡自然；③受格網和鄰域的影響，基于CA的繞障歐氏距離變換結果為繞障至目標最短路徑長度的近似值，采用Butt-Maragos優化算子，誤差比例低于3.96%。計算結果可應用于航線設計、海上救助等領域。

由于誤差的存在，如何通過對變換結果后續處理以改進基于CA的繞障歐氏距離變換的精度，有待進一步研究。