戰時精確情境信息條件下的備件分配模型研究

孫 正，李 峰，戈洪宇

(1.陸軍工程大學石家莊校區， 石家莊 050003； 2.白城兵器試驗中心， 吉林 白城 137000)

戰時裝備備件分配決策是指戰時當裝備發生損傷(自身由于使用、自然磨損以及被敵方攻擊)時，決策機構進行統籌分析后，對備件進行合理分配實現對維修過程的快速響應[1]。由于戰時戰場情形多變，這種變化隨時會對已經制定好的備件分配方案造成影響。這也就意味著裝備保障機關，要根據戰時裝備使用分隊的收集到的精確戰場實時情境信息，制定合理有效的備件分配方案，保證決策結果的實時有效性。學者們也圍繞這一問題進行了大量研究。

從模型角度來說，王威[2]考慮了單個需求點的軍械裝備備件分配決策多層規劃模型，建立了時間最短和時間有限兩個模型，張芳玉[3]對供應決策的影響因素進行了分析，建立了裝備備件供應運力預計和調運模型。宋光明[4]提出了一種基于rough集理論的裝備保障資源配置方法，對戰場環境下資源配置進行了定性分析，給出了多種裝備保障資源配置方案。牛天林[5]借鑒美軍的“精確保障”思想，研究戰時備件問題，為戰時維修管理系統構建提供了思路。閆紅偉[6]針對戰時裝備搶修備件的重要度進行建模。曹繼平[7-8]針對戰場協同搶修時可能發生的搶修資源短缺和資源沖突等問題，分析了連續消耗搶修資源的特點，構建了最早搶修開始時間的救援點最少資源分配決策模型，給出了求解算法和優化方案。從算法角度，范浩[9]通過研究改進遺傳算法，引入了動態小生境狙擊算法，為戰時備件分配決策打下理論和模型基礎。王連鋒[10]考慮戰場資源配送帶有時間窗的路徑問題，提出了改進的多目標粒子群優化算法，并用仿真證明了模型的合理性。部分學者考慮不同軍種裝備會有不同的搶修特點，根據各自特點構建模型。程漢文[11]考慮了防空作戰和戰時維修特點，將戰時維修等待時間作為依據，構建了戰時維修保障資源配置規劃模型。林華[12]分析海上戰場資源分類以及戰場資源特點，在多智能體的基礎上構建了海上戰場資源規劃系統。馮玉光[13]利用基于熵權-模糊層次分析法構建戰時備件供應鏈的運輸績效評價，并利用仿真實際驗證模型的有效性。

鑒于此在構建基于情景的戰時備件的分配模型時，考慮到不同裝備使用分隊的裝備戰損率以及戰損等級分布等因素對有限備件進行分配，本文提出一種基于情境的方法，為戰時部隊裝備保障機關對備件進行分配提供依據。

1 問題描述

根據戰時部隊維修備件保障工作實際需求及特點，本節研究的問題可以抽象為:某次部隊演習或戰斗打響后發生后，從集團軍后方戰略倉庫運送到裝備使用分隊備件需求點的資源，首先匯集到旅級戰役級倉庫;上級機關建立了n個戰術級備件倉庫對執行不同作戰任務的裝備使用分隊提供備件保障，具體備件資源分配流程如圖1所示。由于這些備件倉庫覆蓋戰斗地域的裝備使用分隊裝備與任務數量完全不同，他們的備件需求也會不同。如何根據各倉庫面臨的具體情境，把備件倉庫有限的資源分配給每個裝備使用分隊是急需解決的問題。

圖1 戰時備件資源分配流程

2 研究設計

2.1 模型構建

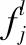
定義1：最優情境：任意裝備使用分隊的各項異構實際情境均為最優值時的情境元素集合。即：

S*=f1*,f2*,…,fL*

(1)

定義2：最差情景：任意裝備使用分隊的各項異構實際情境均為最差值時的情境元素集合，即：

(2)

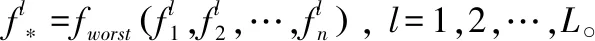
在以上兩個定義中，函數fbest和fworst的解為使得裝備使用分隊獲得最多備件資源與最少備件資源時的方程解。在裝備執行不同任務中，根據實際情況，由于各裝備使用分隊的異構情境因素數值是有較大差別的，所以給出的最優與最差情境有可能不是部隊實際所面對的情境，即可能是虛擬的情境值。

為了使模型的構建更符合實際情況，且不失一般性，下面給出如下假設條件：

假設1：任意戰時所考慮的情境因素數值與因此導致的部隊備件需求數量的關系是正比關系(若是實際分配工作中出現所考慮的實際情境因素與備件需求數量是反比關系，則可以對情境因素取倒數來避免該問題的發生)。

通過假設1，得到推論1與推論2兩條結論：

推論1：當前裝備使用分隊所處的戰斗情境與最優情境距離越小，則該裝備使用分隊對維修備件的需求相對越少；裝備使用分隊戰斗情景與最優情境之間的距離越大，則戰役級備件倉庫對該用裝分隊分配的備件資源相對越多。

推論2：當前裝備使用分隊所處的戰斗情境與最差情境之間的距離越小，該裝備使用分隊對維修備件的需求相對越多；裝備使用分隊戰斗情境與最差情境距離越大，該用裝分隊會分配到更少的備件資源。

這樣得出的各項異構情境因素是不具備數值上的可比性的，為此應當先對所有裝備使用分隊的各項情境因素進行數值歸一化處理，處理過程做如下定義：

(3)

其中：

l=1,2,…,L;j=1,2,…,n

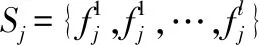
(4)

最差情景距離為

(5)

在確定了每個裝備使用分隊的情境與最優最差情境距離之后，可以給出情境相對近似度定義。

(6)

其中Dj表示最優情境與最差情境之間的距離。

2.2 測度指標

2.2.1 距離測度指標

對分配模型的建模，選擇合適的距離測度函數，是構建基于情境匹配分配模型的核心問題。主要選擇3種主流的距離測度函數對情境值進行相似度計算，分別是標準歐氏距離測度函數、Jaccard距離測度函數和相關系數距離測度函數，然后利用隨機數據，在Matlab仿真軟件中實際驗證三種距離測度函數哪種是最有效且符合實際情境因素的選擇。

1) 標準歐氏距離。標準歐氏距離定義兩個裝備使用分隊的實際情境值的距離為

(7)

其中Sl表示情境因素值的標準差，l=1,2,…,L。

2) Jaccard距離。Jaccard距離主要是基于Jaccard相似度系數所構建的距離測度函數。兩個裝備使用分隊情景Sj和Si，可以將其Jaccard相似度系數定義為：

(8)

其Jaccard距離為

(9)

3) 相關系數距離。相關系數距離是基于相關系數的，即

DCorre=1-ρSiSj=

(10)

其中:ρSiSj表示兩個不同裝備使用分隊的具體情境Sj和Si的相關系數，E()和D()分別表示均值和方差。在計算得出每個裝備使用分隊的情境相對近似度后，對所有數據進行歸一化處理，可以得到每個裝備使用分隊分配的備件比：

(11)

最后，可以得到當前決策時段為裝備使用分隊分配備件數量Qj=Pj·Qtotal。

2.2.2 績效測度指標

戰時維修備件的分配運輸與常規民用物流大相徑庭，對分配備件時的公平性與效率性往往更加側重關注，但在實際過程中卻無法對分配過程是否公平進行具體度量。在戰時備件分配實際中，能否為執行不同任務的用裝分隊分配與之戰斗情景相符的備件資源，則是分配過程公平的重要體現。根據公平性準則，主要提出了兩種用于測量基于情景的備件分配方法的測度指標： 情境與分配的平均相關系數(Average Relevance Coefficient between Situations and Allocations,ARC)和平均相對可分系數(Average Relevance Separability,ARS)，用以體現該模型分配的維修備件數量是否與戰時實際情景相匹配。

1) 情境與分配的平均相關系數(ARC)。在此作以下定義。

定義5：情境與分配的平均相關系數(主要表示為用裝分隊情境因素值與分配的備件比之間的平均相關系數，即：

(12)

其中Rcoef(A,B)表示A和B的相關系數。可以舉一個簡單示例說明平均相關系數的實際含義。假設某次演習過程中有5個執行不同任務的用裝分隊(A1,A2,…,A5)，裝備機關對這5個分隊分配備件時所考慮的的情境因素主要是：裝備損傷比例與該分隊裝備總數量。如果兩個分隊的裝備損傷比相同，那么為該分隊分配的備件數量應該與各分隊的裝備總量相符；若是兩個分隊的裝備總數量相等，則為其分配的備件資源數量應該與其裝備損傷比相符。若想要同時考慮兩種以上不同情境因素，那么為不同裝備使用分隊分配的備件數量應該與情境因素值的平均相關系數相符。由此可見，不同情景下的ARC系數越高，代表裝備機關分配的備件數量與該裝備使用分隊所面臨的實際情況更加相符。

定義6：任意情境因素的可分性SSl為所有裝備使用分隊不同取值的個數除以裝備使用分隊的總數量，即：

(13)

式(1)中的sumproduct(A)函數代表A中任意兩個不相等的因素個數。

定義7：分配比可分性RS為不同備件配置百分比的數字值個數除以所有用裝分隊數量，即：

(14)

在對上述兩種可分性定義之后，給出平均相對可分性系數的定義，即：

定義8：平均相對可分系數是SSl與RS的平均差，即：

(15)

由此看出，ARS越小，備件分配比與用裝分隊面臨的實際情況越相符。

3 數據驗證

為了驗證上述模型的有效適用性，利用Matlab軟件進行隨機數據的仿真驗證，并對結果進行分析。假設在某次演習中，部隊共派出60個執行不同任務類型的任務分隊進行演習。利用軟件隨機生成這60個任務分隊的位置坐標，任務分隊的橫縱坐標值均由Matlab軟件在[0～200]隨機產生，生成坐標位置如圖2所示，本節擬驗證在戰時將有限的備件資源分配給具有不同情境的60個用裝分隊。

圖2 戰役級倉庫(六角形)與用裝分隊(五角星)分布

戰時的備件分配所考慮的每個裝備使用分隊所面對的具體情境是各有不同的，裝備保障機關在實際分配工作中往往要考慮很多不同方面的因素，例如裝備戰損情況，執行任務數量，后方倉庫備件數量，運輸道路損毀狀況等。從現有研究文獻資料來看，本節主要考慮六種不同的戰時情境因素，如表1所示(本文主要側重于研究面對當前各項異構情境因素，如何對有限的備件資源進行分配，使備件保障效能最高，并不考慮哪些情境因素是具體需要的。

表1 分配搶修資源時所考慮的情境因素

為模型構建不失一般性，現根據當前文獻研究確定所有情境因素范圍界定(如表2第2行所列)，利用軟件隨機生成所有情境因素具體數值，具體如表2所示。通過表格，可以看到表格所給的6種不同情景因素為異構數據，且單位與量級均不相同。隨機生成的60個用裝分隊的各項情境并不相同。根據定義1與定義2，最優情境與最差情景分別為：S*={0.30,0.10,0.00,661,2 156,5}和S*={0.60,0.29,0.10,1 990,9 999,29}。即最優情境因素為具有最低裝備輕損比(0.6)，最低的裝備中損比(0.29)，最低的裝備重損比(0.10)，最少的裝備搶修時間(661)，最少的裝備備件總數量(2 156)以及最低的裝備執行任務數量(5)。最差情境因素為最高裝備輕損比(0.3)，最高的裝備中損比(0.1)，最高的裝備重損比(0.00)，最多的裝備搶修時間(1 990)，最多的裝備備件總數量(9 999)以及最多的裝備執行任務數量(29)。

根據分配模型，具有最差與最優情境因素的裝備使用分隊應當被分配最多和最少的維修備件資源。當前分隊所處情境與最優與最差情境之間的相對近似度決定了為每個用裝分隊分配的備件比：與最優情境相對近似度越大，應當分配更少備件，越接近最差情境應當分得更多備件資源。本文采用相對近似度用以衡量接近度的大小，如定義4所述。根據式(1)～式(6)可以計算得出每個用裝分隊的與最優最差情境的接近度大小，然后利用式(11)計算為每個用裝分隊分配的備件比，具體可見表3(假設當前后方倉庫可供分配備件資源數量為50 000單位)。

表2 用裝分隊實際情境因素隨機生成值

表3 相對近似度備件分配結果

續表(表3)

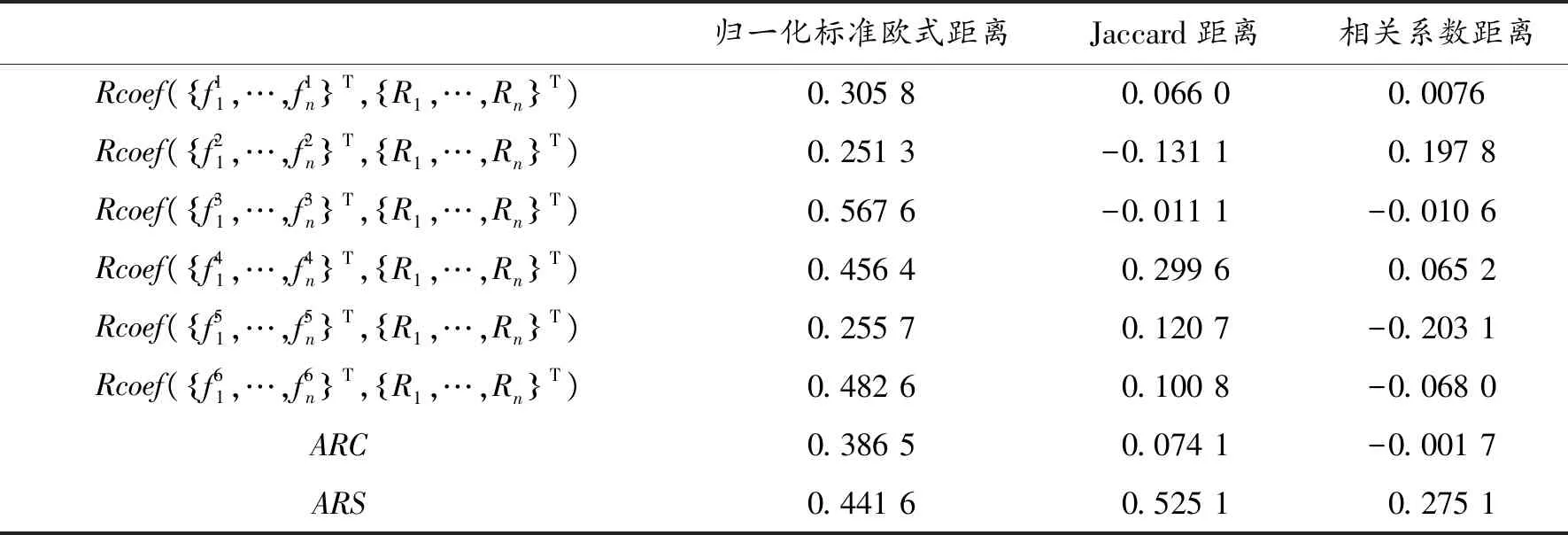
表4 不同測度函數下分配結果的ARCs和ARSs

圖3至圖5給出了基于不能距離測度函數的備件分配結果。從分配結果來看：Jaccard距離測度函數在為60個分隊提供的備件分配比只有兩種，這顯然是與實際情況不相符的，其他兩種情況均比較符合實際分配比，但究竟哪種是最符合需求的分配方式，通過表4可以看出：不同測度函數下的ARCs與ARSs均不相同，具有較大ARCs系數與較小ARSs系數的測度距離函數得出的是最優的分配結果。由此來看，歸一化標準歐式距離測度函數明顯比Jaccard距離測度函數所分配的備件比更加合理。歸一化標準歐氏距離的ARC在三種分配結果下是最大的，雖然ARS也是最大，但與相關系數距離所得的分配結果相比較，相關系數距離所得到的ARC是負數，這明顯是不合適的。綜上，得出利用歸一化標準歐氏距離測度函數所得的分配結果為最佳選擇，且與實際情境最相匹配。

圖3 基于標準歐氏距離的備件分配結果

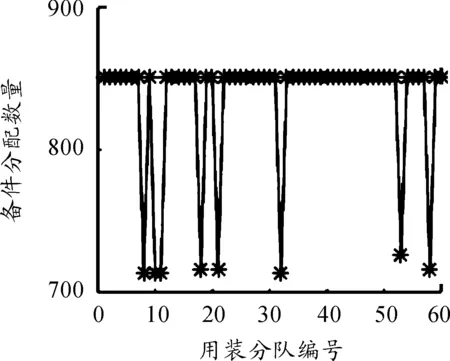
圖4 基于Jaccard距離的備件分配結果

圖5 基于相關系數距離的備件分配結果

4 結論

針對戰時備件資源數量的不足性、戰時數據的不完整性、影響因素的異構性等，分別計算了在三種不同距離測度函數下的備件分配比，找到了最優距離測度函數。提出了基于情境的戰時備件分配方法；針對戰時備件分配比分配不均，構建情境與分配的平均相關系數(ARC)和平均相對可分系數(ARS)兩個績效指標，計算出每個裝備使用分隊分配的備件比與其情境的相符程度。實驗結果發現：歸一化標準歐氏距離方法能夠產生與情境最匹配的分配方案，符合戰時備件分配工作實際，為戰時備件實施精確分配提供了一個有效的計算模型，大大提高了備件分配工作的效率與精確性，也為后續深入研究提供了距離測度依據。