基于fluent的一級(jí)氣體炮內(nèi)彈道研究

熊 鎬，王惠源，王海旭

(中北大學(xué) 機(jī)電工程學(xué)院， 太原 030051)

氣體炮是一種利用壓縮氣體做為動(dòng)力源推動(dòng)彈丸運(yùn)動(dòng)的發(fā)射裝置，相比于以火藥做為動(dòng)力源的傳統(tǒng)火炮，氣體炮在獲得較高初速的同時(shí)，不存在火炮發(fā)射時(shí)高溫高壓，發(fā)射相對(duì)穩(wěn)定，安全可靠，且彈丸膛內(nèi)運(yùn)動(dòng)時(shí)，需要承受的加速度和應(yīng)力較小，炮身也不需要承受高溫特性，使用壽命長(zhǎng)。

現(xiàn)有主要的一級(jí)氣體炮內(nèi)彈道模型有兩種，一種是基于等溫膨脹假設(shè)的模型[1]，一種是基于絕熱膨脹假設(shè)的模型[2]，后一種適用范圍更廣。這兩種模型都是根據(jù)火炮內(nèi)彈道模型演化而來(lái)，且都用平均膛壓作為彈底壓力計(jì)算彈丸運(yùn)動(dòng)情況，再采用次要功系數(shù)對(duì)模型進(jìn)行修正。李鋒等[3]在絕熱膨脹模型的基礎(chǔ)上，提出一種基于密度均勻假設(shè)的內(nèi)彈道模型修正方案，考慮了氣室容積對(duì)內(nèi)彈道的影響，得到一種更準(zhǔn)確的內(nèi)彈道模型。這些模型都沒有考慮閥門對(duì)膛內(nèi)氣流的影響。Z.J.Rohrbach等[4]提出一個(gè)根據(jù)通過(guò)閥門的氣體流量計(jì)算氣體炮內(nèi)彈道的模型，并通過(guò)實(shí)驗(yàn)驗(yàn)證；文獻(xiàn)[13]中也對(duì)閥控氣體炮內(nèi)彈道進(jìn)行了研究，但這兩種針對(duì)閥門流量的內(nèi)彈道計(jì)算都是在有一定實(shí)驗(yàn)基礎(chǔ)的前提下針對(duì)固定氣體炮的內(nèi)彈道計(jì)算。

為了研究氣體炮內(nèi)彈道過(guò)程中膛內(nèi)氣體流動(dòng)狀態(tài)，分析閥門對(duì)氣體炮的影響，筆者利用計(jì)算流體力學(xué)商業(yè)軟件fluent建立氣體炮CFD模型，仿真分析了內(nèi)彈道過(guò)程中氣體炮膛內(nèi)氣體流動(dòng)狀態(tài)和彈丸的運(yùn)動(dòng)狀態(tài)。

1 內(nèi)道模型

氣體炮工作時(shí)，氣室內(nèi)充滿高壓氣體，當(dāng)閥門打開，彈丸在高壓氣體的推力作用下沿著身管向前。圖1所示為氣體炮結(jié)構(gòu)簡(jiǎn)化模型。

圖1 一級(jí)氣體炮基本結(jié)構(gòu)簡(jiǎn)化模型

式(1)和式(2)分別為氣體炮在絕熱膨脹假設(shè)下和等溫膨脹假設(shè)下的內(nèi)彈道方程。假設(shè)氣體為理想氣體，通過(guò)氣體動(dòng)力學(xué)計(jì)算膛內(nèi)平均壓力，并引入虛擬質(zhì)量系數(shù)φ，計(jì)算各類能量損失，最后根據(jù)牛頓運(yùn)動(dòng)定律積分得到[1,2,5]。

絕熱膨脹假設(shè)下的內(nèi)彈道方程：

(1)

等溫膨脹假設(shè)下的內(nèi)彈道方程：

(2)

式(2)中：vm為彈丸初速；k為氣體絕熱指數(shù)；A為身管截面積；m為彈丸質(zhì)量。

其中，次要功系數(shù)φ的表達(dá)式為

(3)

式(3)中：K為與摩擦力、彈丸旋轉(zhuǎn)等能量有關(guān)的修正系數(shù)，本文中取1.05；式(3)等式右邊第二項(xiàng)為氣體動(dòng)能修正，mg為氣體質(zhì)量，可通過(guò)氣體狀態(tài)方程方程得到。

2 CFD模型

2.1 控制方程

假設(shè)流體不可壓縮，通過(guò)對(duì)連續(xù)性方程和動(dòng)量守恒方程的求解來(lái)獲得膛內(nèi)流場(chǎng)的數(shù)值模擬。連續(xù)性方程和動(dòng)量守恒方程[6]為

(4)

(5)

其中：p為靜壓；ρgi、Fi為重力體積力和其他體積力；τij為應(yīng)力張量。

采用的湍流模型為RNG(重正化群)k-ε模型[7]，湍動(dòng)能k方程和湍能耗散率ε方程與標(biāo)準(zhǔn)k-ε方程相似，即：

(6)

(7)

其中：

μeff=μ+μt

(8)

(9)

(10)

(11)

(12)

其中：Gk為平均速度梯度所引起的湍動(dòng)能生成項(xiàng)；經(jīng)驗(yàn)常數(shù)C1ε、C2ε、η0、β取值分別為1.42、1.68、4.377、0.012。

2.2 計(jì)算模型、網(wǎng)格劃分及計(jì)算方法

本文選用空氣做為氣體工質(zhì)，空氣的相關(guān)參數(shù)：k=1.4，摩爾質(zhì)量μmol=0.002 806 4 kg/mol。計(jì)算模型如圖2所示，其中氣室容積V0=1.8 L，身管長(zhǎng)L1=1 m，閥門與彈底的距離L2=5 mm，口徑D=35 mm，彈重m=0.3 kg，氣室初始?jí)毫0=10 MPa，初始溫度為300 K。

為了達(dá)到提高計(jì)算效率的目的，本文將三維模型簡(jiǎn)化為二維模型計(jì)算。本文主要關(guān)注氣體炮膛內(nèi)氣體流動(dòng)狀態(tài)，由于彈丸膛內(nèi)運(yùn)動(dòng)速度較低，不會(huì)在彈前形成激波，相比于彈底壓力，彈前空氣阻力忽略不計(jì)。

動(dòng)網(wǎng)格模型是用來(lái)模擬由于計(jì)算域邊界運(yùn)動(dòng)而引起的計(jì)算域形狀隨時(shí)間改變問題的流體流動(dòng)。動(dòng)網(wǎng)格模型的關(guān)鍵技術(shù)是網(wǎng)格重新生成方法，本文同時(shí)采用彈簧光順和局部網(wǎng)格重構(gòu)兩種方法，當(dāng)變形較小時(shí)，采用彈簧光順方法，當(dāng)變形增大時(shí)，采用局部網(wǎng)格重構(gòu)來(lái)避免網(wǎng)格質(zhì)量下降[6]。網(wǎng)格模型如圖3所示，網(wǎng)格數(shù)據(jù)為：網(wǎng)格數(shù)138 523個(gè)，節(jié)點(diǎn)數(shù)46 175個(gè)。

圖2 氣體炮計(jì)算模型

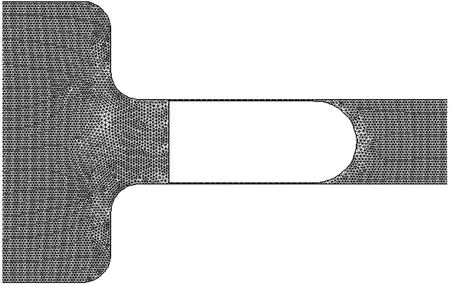
圖3 彈體周圍網(wǎng)格模型

由于閥門結(jié)構(gòu)不同，且開啟過(guò)程時(shí)間極短，這里忽略閥門開啟過(guò)程，即假設(shè)閥門瞬間開啟，在模型中不建閥門的模型，而是在fluent中利用patch功能定義閥門后的氣室壓力和閥門前的大氣壓力，實(shí)現(xiàn)閥門完全開啟瞬間的壓力條件。

在fluent中利用用戶自定義函數(shù)(UDF)讀取彈底壓力變化和定義摩擦阻力，利用DEFINE_CG_MOTION函數(shù)賦予彈丸膛內(nèi)運(yùn)動(dòng)。湍流模型選用上述的RNG(重正化群)k-ε模型，綜合考慮計(jì)算的效率和精度，壓力和速度耦合方法采用coupled算法，Green-Gauss Node Based壓力方程利用PRESOT方法離散，動(dòng)量方程，湍動(dòng)能耗散率等均采用而二階迎風(fēng)方程(Second Order Upwind)來(lái)計(jì)算。

由于膛內(nèi)氣流流動(dòng)狀態(tài)變化迅速，從閥門打開到彈丸出膛口，總的時(shí)間約為10 ms，UDF通過(guò)讀取彈體表面壓力計(jì)算彈丸在時(shí)間步內(nèi)的速度，一方面單位時(shí)間過(guò)長(zhǎng)會(huì)造成本應(yīng)該在時(shí)間步內(nèi)降低的壓力保持一定，導(dǎo)致計(jì)算結(jié)果不準(zhǔn)確，另一方面，隨著速度的增加，單位時(shí)間內(nèi)運(yùn)動(dòng)的距離增大，會(huì)導(dǎo)致網(wǎng)格變形增大，不利于計(jì)算精度。本文根據(jù)多次計(jì)算分析，選1×10-7s的時(shí)間步長(zhǎng)。

3 計(jì)算結(jié)果與分析

圖4和圖5是有閥門和無(wú)閥門兩種結(jié)構(gòu)下的膛內(nèi)氣流速度云圖和壓力云圖，圖中所示為彈后空間內(nèi)氣體流動(dòng)狀態(tài)。

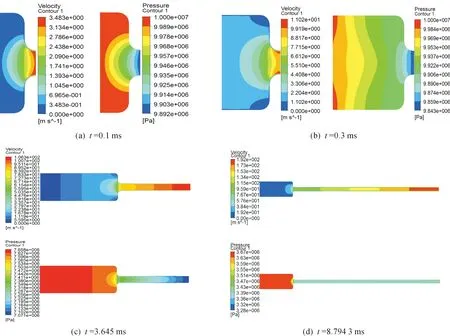
圖4 無(wú)閥門時(shí)膛內(nèi)氣體流動(dòng)狀態(tài)

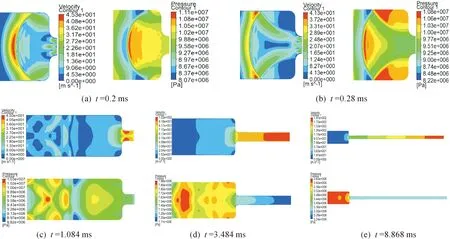
圖5 有閥門時(shí)膛內(nèi)氣體流動(dòng)狀態(tài)

內(nèi)彈道計(jì)算中，假設(shè)膛內(nèi)氣體速度線性線性分布[8]，即：

(13)

式中：u為膛內(nèi)內(nèi)任意位置的速度。

由圖4速度云圖可以看出，無(wú)閥門時(shí)，彈后空間中，身管內(nèi)的氣體基本保持線性分布，但是在氣室與身管連接處存在較大的速度梯度，這是由于身管與氣室連接處存在較大的收縮比，由氣體動(dòng)力學(xué)理論可知，亞聲速氣流在截面積逐漸縮小的管道內(nèi)將不斷加速[9]，傳統(tǒng)火炮內(nèi)彈道計(jì)算假設(shè)膛內(nèi)氣體速度線性分布，一方面火炮膛壓高，氣流速度較快；另一方面，火炮彈膛與身管截面積變化較小，截面積變化對(duì)膛內(nèi)氣流的影響較小。對(duì)于同一種氣體工質(zhì)，在相同溫度下，氣體做工能力主要和壓力和氣室容積相關(guān)[10]，因此，氣體炮往往有極大的氣室容積和收縮比，氣體炮內(nèi)彈道計(jì)算不能只考慮膛內(nèi)氣流線性分布，還應(yīng)充分考慮收縮比變化對(duì)氣體流動(dòng)狀態(tài)的影響。

圖5所示為有閥門時(shí)膛內(nèi)氣體流動(dòng)狀態(tài)，可以看出，閥門打開后，氣體先是向前流動(dòng)(身管指向?yàn)榍?，當(dāng)氣流流到彈底時(shí)，彈丸開始運(yùn)動(dòng)，由于氣流速度遠(yuǎn)高于彈丸速度，氣體開始回流，當(dāng)回流與來(lái)流相遇，形成彈后氣體復(fù)雜流動(dòng)狀態(tài)，經(jīng)過(guò)極短時(shí)間后，彈后氣體形成向氣室底部傳遞的激波，一方面，來(lái)流與回流相遇形成氣室中心的激波，激波前后有壓差和速度差造成了圖5中的壓力云圖與速度云圖的局部斷面，另一方面，激波在氣室壁面上的反射使壁面附近形成高壓區(qū)域，激波在膛內(nèi)的反復(fù)傳遞形成了膛內(nèi)壓力和氣流速度的不均勻。

圖6所示為彈后壓力的變化曲線，可以看出，有閥門結(jié)構(gòu)時(shí)，彈底壓力在閥門打開時(shí)，先是迅速的上升，達(dá)到了最大約12.2 MPa的彈底壓力，之后在11 MPa上下劇烈的變化，直到約0.2 ms，彈底壓力開始下降，然后保持一定的規(guī)律在無(wú)閥門結(jié)構(gòu)彈底壓力曲線上下波動(dòng)，直到約3.5 ms，隨著彈丸速度和位移的增加，彈丸逐漸遠(yuǎn)離氣室，氣室內(nèi)氣流的波動(dòng)對(duì)管內(nèi)氣流的影響逐漸減小,彈底壓力逐漸趨于穩(wěn)定，并且與無(wú)閥門結(jié)構(gòu)的彈底壓力一致。由圖6、圖7可以看出：無(wú)閥門結(jié)構(gòu)與有閥門結(jié)構(gòu)在內(nèi)彈道初期，彈底壓力有較大的不同，但是整個(gè)內(nèi)彈道過(guò)程中，有閥門結(jié)構(gòu)的壓力曲線主要在無(wú)閥門結(jié)構(gòu)彈底壓力曲線上下波動(dòng)，最終保持一致，彈丸運(yùn)動(dòng)速度始終保持較高的一致性。

圖6 彈底P-t曲線

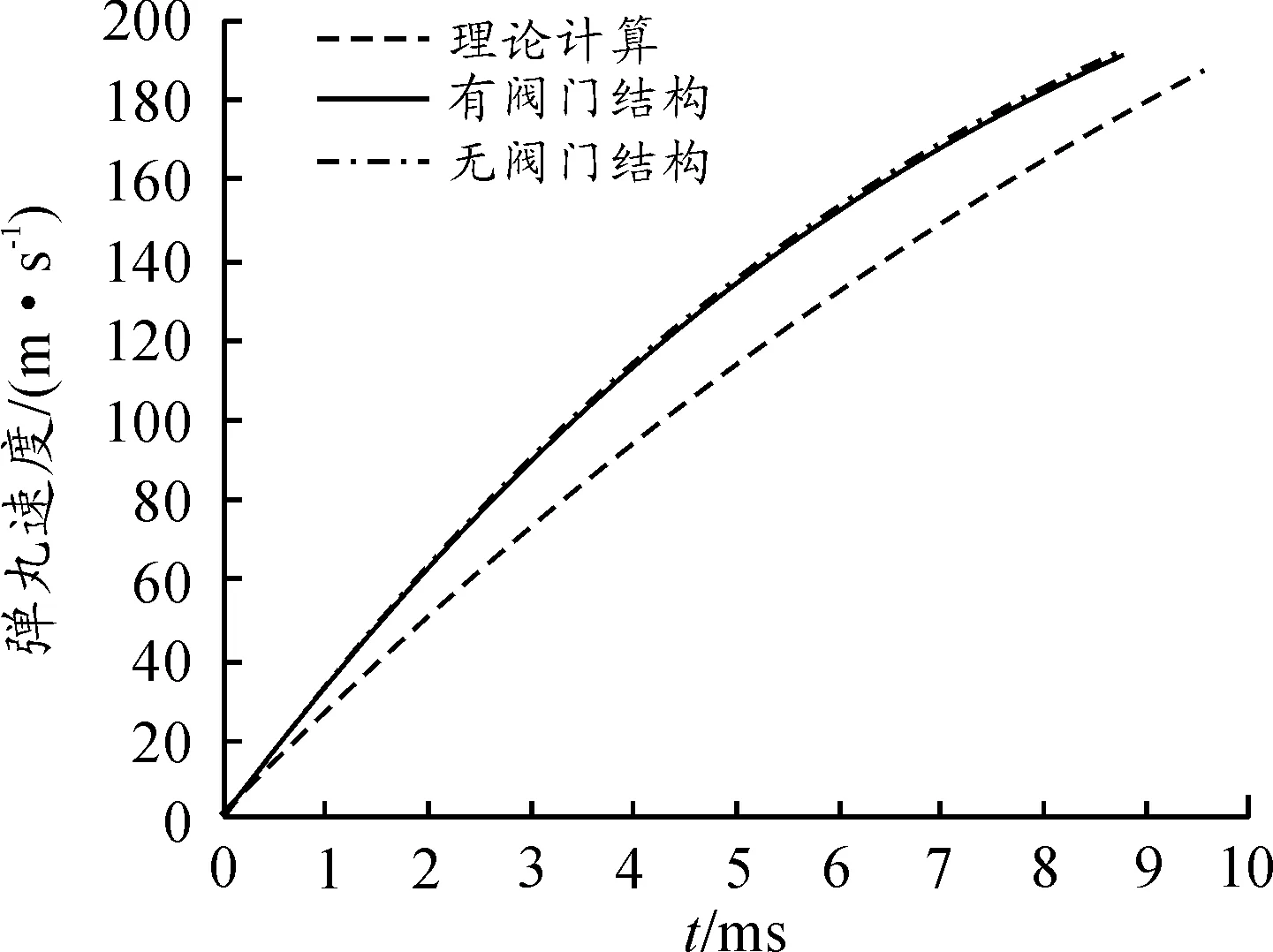
圖7 彈丸v-t曲線

圖6、圖7、圖8中理論內(nèi)彈道模型與仿真結(jié)果可以看出：膛內(nèi)平均壓力與仿真結(jié)果的彈底壓力有較大的區(qū)別，內(nèi)彈道計(jì)算中用次要功系數(shù)與平均壓力計(jì)算彈丸運(yùn)動(dòng)情況，計(jì)算出的彈底壓力與仿真結(jié)果仍有較大的誤差，且彈丸速度也遠(yuǎn)低于仿真結(jié)果。

表1所示為彈丸初速的對(duì)比結(jié)果可以看出：與實(shí)驗(yàn)數(shù)據(jù)相比，fluent仿真結(jié)果與理論計(jì)算模型有相同的彈丸速度變化規(guī)律，且仿真結(jié)果與實(shí)驗(yàn)結(jié)果的誤差很小，相比于理論計(jì)算的結(jié)果更接近實(shí)驗(yàn)結(jié)果。由圖4可以看出，氣流在身管與氣室連接處有較大的速度和壓力梯度，式(3)中氣體動(dòng)能項(xiàng)未考慮氣室容積和收縮比造成的膛內(nèi)氣流狀態(tài)變化，從而造成彈底壓力計(jì)算不準(zhǔn)確。

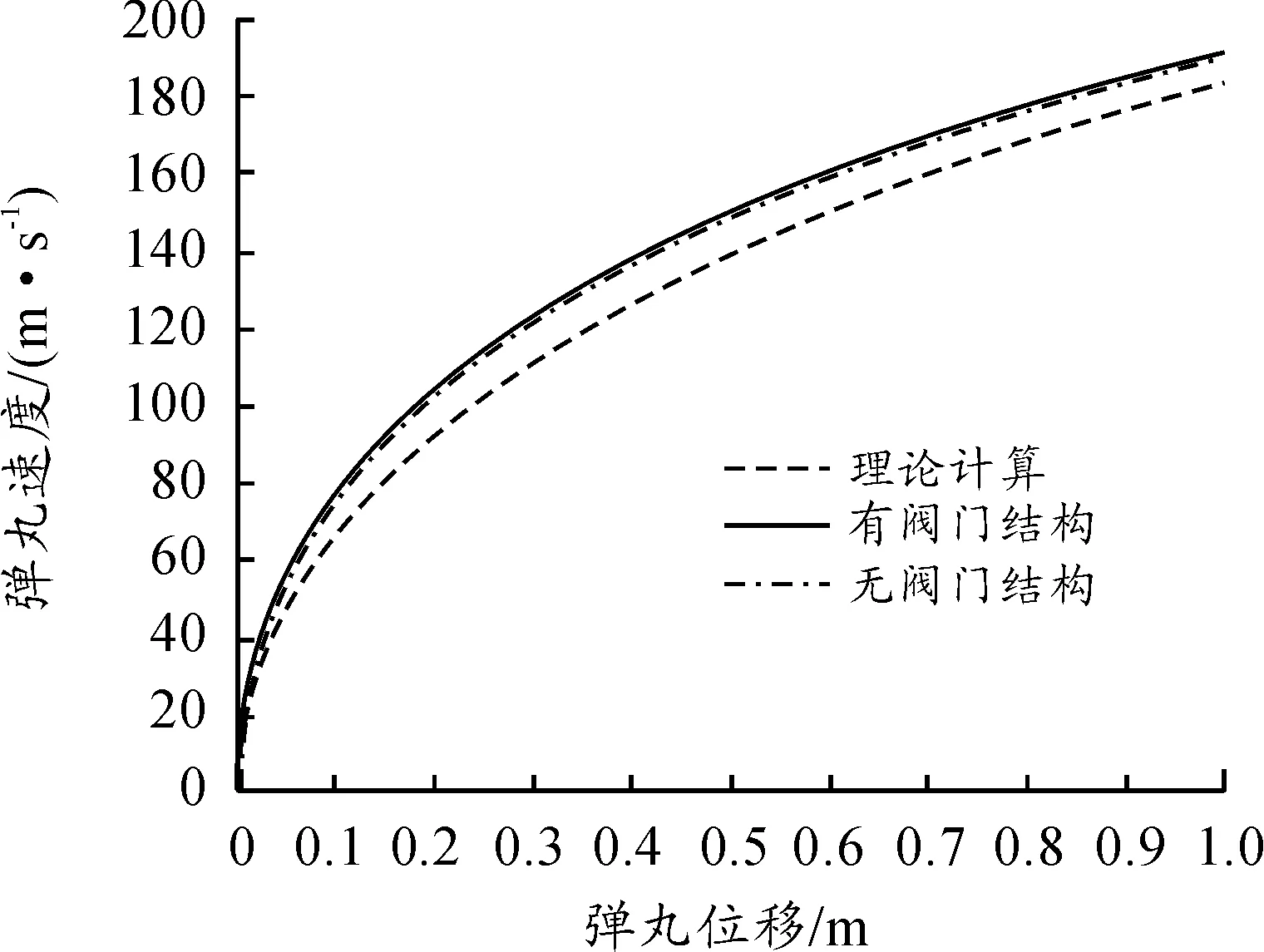
圖8 彈丸v-L曲線

仿真結(jié)果有閥門無(wú)閥門理論計(jì)算實(shí)驗(yàn)結(jié)果平均初速12345速度/(m·s-1)191.9192.2186.1192.8194.01193.97192.49192.36時(shí)間/ms8.8688.79439.7—

4 結(jié)論

本文利用fluent動(dòng)網(wǎng)格技術(shù)和UDF對(duì)氣體炮內(nèi)彈道過(guò)程進(jìn)行了仿真，有閥門結(jié)構(gòu)會(huì)造成彈底氣體回流，內(nèi)彈道初期彈底壓力反復(fù)變化，但是隨著彈丸速度和位移增加，氣室內(nèi)氣流運(yùn)動(dòng)對(duì)彈丸影響減小，彈底壓力逐漸與無(wú)閥門結(jié)構(gòu)的彈底壓力一致，兩種結(jié)構(gòu)的彈丸速度變化情況基本一致。但閥門會(huì)影響膛內(nèi)氣流狀態(tài)，當(dāng)身管長(zhǎng)度較小時(shí)，應(yīng)盡量減小彈底與閥門的距離，減小氣流加速距離，減小對(duì)氣體流動(dòng)狀態(tài)的影響。

對(duì)比仿真結(jié)果和現(xiàn)有內(nèi)彈道計(jì)算模型，認(rèn)為現(xiàn)有計(jì)算模型在彈底壓力計(jì)算上未考慮氣室容積和收縮比對(duì)膛內(nèi)氣流的影響，導(dǎo)致彈丸運(yùn)動(dòng)速度計(jì)算結(jié)果低于實(shí)際結(jié)果，fluent仿真的結(jié)果相比于理論模型更接近實(shí)驗(yàn)結(jié)果，在氣體炮內(nèi)彈道的研究上具有一定的可信度。