指數型單元貯存壽命分布參數的貝葉斯估計方法及仿真分析
李 婧,朱曉軍,李 華
(1.海軍工程大學 管理工程與裝備經濟系, 武漢 430033;2.海軍工程大學 艦船與海洋學院, 武漢 430033;3.海軍工程大學 兵器工程學院, 武漢 430033)
對于絕大多數的民用與軍用產品而言,產品出廠后通常都是立即投入使用或服役,產品在其整個壽命周期中基本上都處于工作狀態。因此,人們關心的往往只是其工作可靠性指標,而忽視了其貯存可靠性指標。但是,值得注意的是,有些產品特別是軍用武器裝備,如導彈、水雷和魚雷等,出廠交付后,必須在岸基倉庫、艦倉、甚至發射體或運載體上長期貯存,只有在接到任務命令后才能投入使用,進入戰斗工作狀態[1-3]。對這些武器裝備,我們不僅要關注其工作可靠性指標,而且還更加關注其貯存可靠性指標,而貯存壽命就是裝備貯存可靠性的一個重要參數。
貯存壽命通常是指在規定的貯存條件下裝備從開始貯存到給定可靠度時所對應的時間[4]。本文中,我們將貯存壽命定義為產品從開始貯存到發生故障所經歷的時間。能夠較為準確地預測出武器裝備的貯存壽命,不但有利于減少武器裝備的貯存費用、節約資源,而且可以為裝備的檢修提供正確的決策依據,在提高貯存裝備完好性的同時減少后勤保障費用[5]。
國內外對于貯存壽命的研究一方面通過加速壽命試驗、加速退化試驗[6-7]等貯存可靠性試驗結果分析獲得;另一方面是基于信息融合技術將性能退化理論和可靠性評估的傳統方法相結合,利用多方面數據的綜合預測方法[8-9]。這些方法都比較成熟,但在我軍裝備貯存管理的實際環境下可操作性不強。本文介紹了一種利用實際貯存期間的檢測結果數據,基于貝葉斯推斷來估計指數型單元貯存壽命分布參數的方法。使用該方法可以對裝備中的指數型壽命件的貯存壽命分布規律做出較為準確地估計,達到采用使用階段數據對初始的可靠性指標進行修正的目的,進而為開展裝備貯存效果評估和裝備延壽、定壽等重要問題的決策提供理論依據和數據支持。
1 指數型單元貯存壽命問題描述
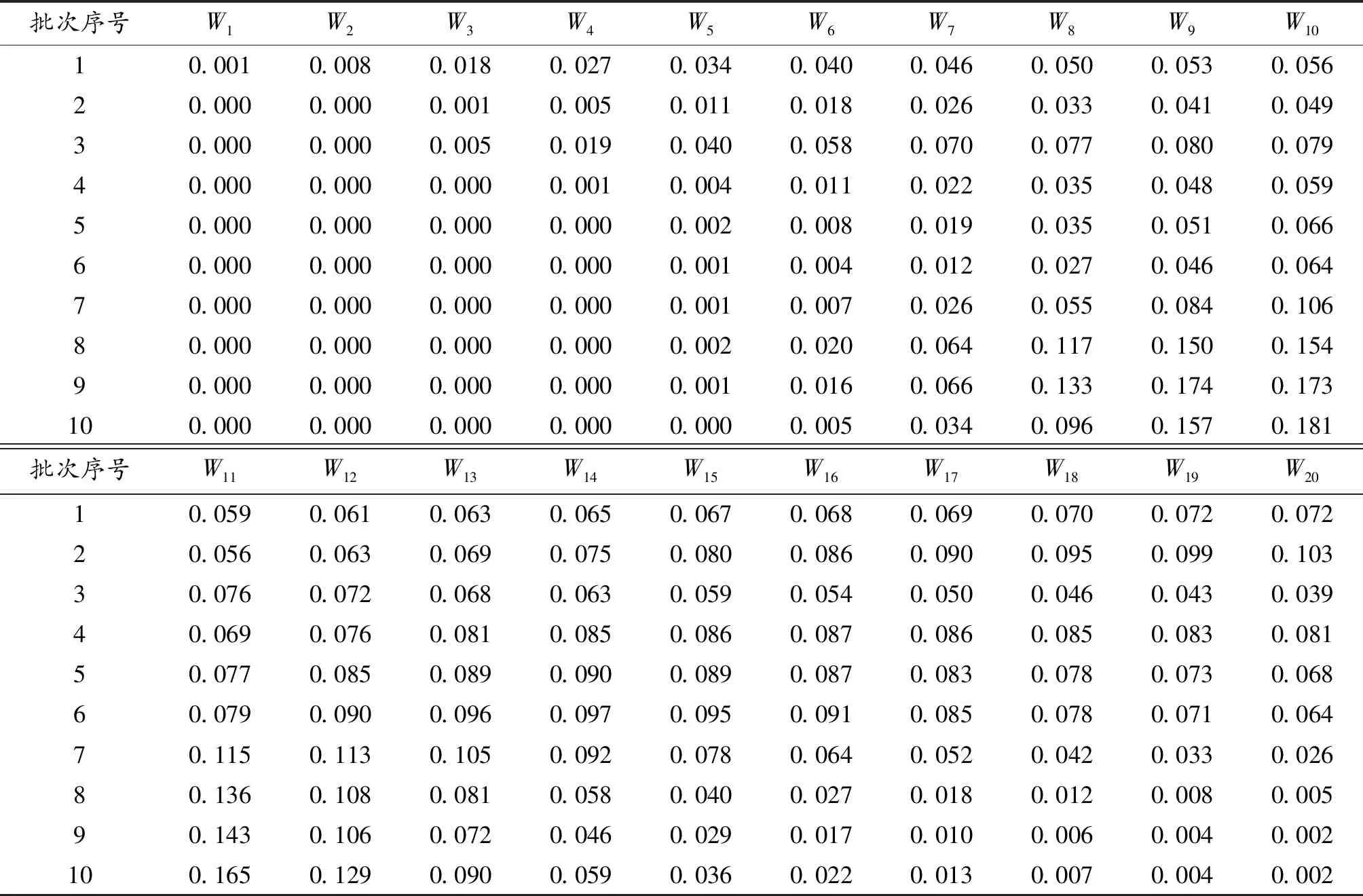
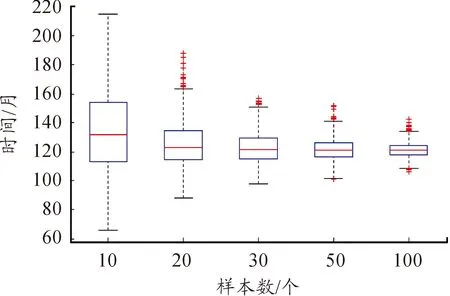
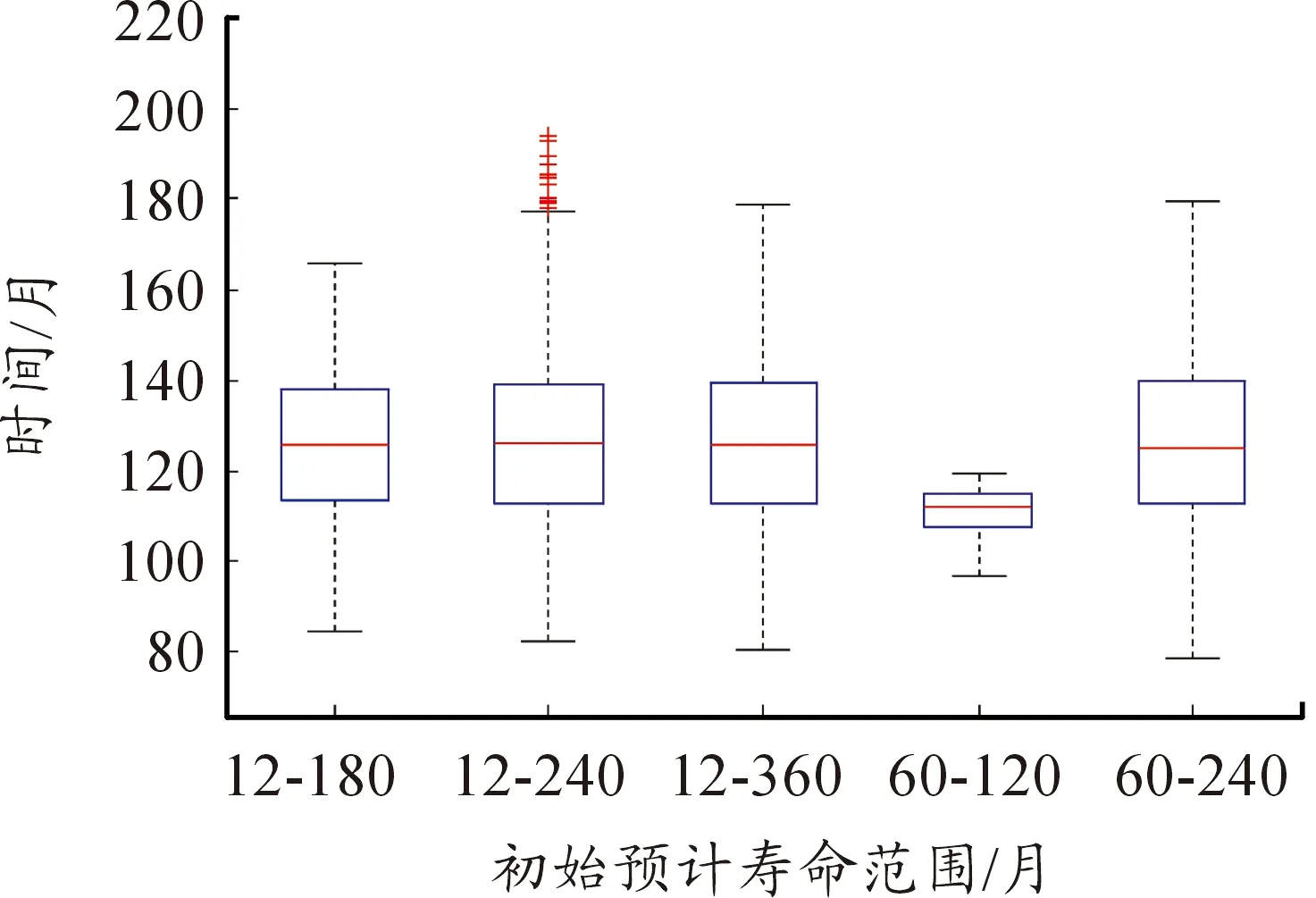
魚雷、水雷和導彈等武器都是一種長期處于貯存狀態的武器裝備,通常被稱為長期貯存裝備。以魚雷為例,由于魚雷貯存時間往往長達數年、單價昂貴,因此在時間和經濟成本上都難以通過理論上的貯存試驗(需要試驗時間足夠長、樣本數量足夠多)來獲得準確的魚雷貯存壽命分布參數。而且,在整個貯存期間,無論是針對整條魚雷還是組成魚雷的各個單元,都無法做到實時在線連續檢測,而只能在離散的檢測時間點Tc得到魚雷(或魚雷單元)“完好”或“故障”的結論。我們將武器裝備的貯存壽命記為T0,則通過離散檢測只能得到貯存壽命T0>Tc(檢測結果為“完好”)或T0 很多貯存裝備,比如魚雷,由于價格昂貴、貯存量較少,可獲得的貯存檢測數據很少,具有典型的小子樣特點,且這種檢測結果數據屬于區間數據。而貝葉斯理論既是一種應用廣泛的小子樣理論,又便于通過似然函數處理區間數據,它可以充分地利用先驗分布和試驗樣本信息有效融合綜合評定,在有限的樣本下提高評估精度。 記指數型單元的平均貯存壽命為t0,共有m批次的檢測結果,第i次的檢測結果用[cTiN1iN0i]表示,cTi表示該批次的樣本單元從開始貯存到本次檢測的已貯存時間,N1i表示本次檢測結果為完好的單元數量,N0i表示本次檢測結果為故障的單元數量。則本文對指數型單元貯存壽命分布參數的估計模型由以下主要步驟組成: 步驟1 生成n個候選的失效率參數λj,1≤j≤n。 (1) 式(1)中,n的取值取決于對T0的估計精度要求。 步驟3 遍歷各個批次的檢測結果,用后驗信息修正權重系數Wj。 1) 令i=1。 2) 根據第i次的檢測結果yi=[cTiN1iN0i],對所有候選的失效率參數λj,計算P1j= e-λj · cTi,P0j= 1-P1j,Pj=P1jN1i·P0jN0i,則 (2) 式(2)中,Pj定量描述了檢測結果[cTiN1iN0i]發生的似然程度;cTi表示樣本單元從開始貯存到第i次檢測的已貯存時間;N1i表示第i次檢測結果為完好的單元數量;N0i表示第i次檢測結果為故障的單元數量。 3) 利用貝葉斯公式計算各候選失效率參數λj的后驗概率πλj|yi,修正權重系數Wj,得到: (3) 4) 令i=i+1,若i≤m則執行2),否則執行步驟4。其中,m表示共有m次檢測結果。 (4) 為表達方便,假定每次檢測的總樣本數量都為10。假定某指數型單元的平均貯存壽命為120個月,每6個月進行一次檢測,共做了10次抽樣檢測,檢測結果如表1。 表1 貯存檢測結果 指數型單元貯存壽命分布參數估計過程如下: 3) 遍歷各個批次的檢測結果,修正權重系數Wj。計算結果如表2。 表2 算例基于歷次檢測數據的權重系數貝葉斯調整結果 可采用下述仿真模型,來模擬樣本總數量為S的貯存過程和第i次的檢測結果。 步驟2:在這組隨機數Xs中找到所有大于cTi的隨機數,記其數量為N1i,令N0i=S-N1i。 圖1為本方法關于本文算例參數大量仿真驗證結果的箱線圖。從仿真結果得出該指數型單元的平均貯存壽命的估計均值為133.2、根方差為26.4,說明獲得的平均貯存壽命的仿真結果與算例中設定的平均貯存壽命120個月在估計精度范圍內是比較一致。 圖1 基于算例參數的平均貯存壽命仿真結果的箱線圖 使用上述仿真模型,下面分析本文方法對壽命分布參數估計精度的主要影響因素。 1) 檢測的樣本數量對估計精度的影響。 逐漸增加樣本數量為20,30,50 和100,將分別得到的平均貯存壽命估計值利用Matlab繪制多重箱線圖如圖2。由圖2可以看出,樣本數量少量的增加就可以使估計精度大幅度提高,如樣本數為20時,平均貯存壽命的估計均值約為128、根方差約為16;樣本數為50時,平均貯存壽命的估計均值約為123(與真值120非常接近)、根方差約為11。 圖2 不同樣本數量下對平均貯存壽命仿真結果的多重箱線圖 2) 檢測次數對估計精度的影響。 取樣本量為10(保持樣本較少數量),保持檢測間隔不變(6個月),逐漸增加檢測次數為10,15,20 和25,將分別得到的平均貯存壽命估計值,利用Matlab繪制多重箱線圖如圖3所示。由圖3可以看出,檢測次數這一因素對估計精度影響的靈敏度很高,隨著檢測次數的少量增加估計精度有很大提高,當檢測次數增加為25時,平均貯存壽命的估計均值約為121.412 5、根方差約為7.831 0,與真值非常接近。可見,檢測間隔不變的情況下,檢測次數的增加使得數據對裝備壽命區間覆蓋率增高,壽命預測會更精確,這與實際情況相符。 圖3 不同檢測次數對平均貯存壽命仿真結果的多重箱線圖 3) 檢測間隔對估計精度的影響。 取樣本量N0i+N1i=10(保持樣本較少數量),檢測次數m=10,將檢測間隔(單位:月)分別選為3,6,12和18,將分別得到的平均貯存壽命估計值,利用Matlab繪制多重箱線圖如圖4所示。由圖4可以看出,本文方法對檢測間隔并沒有要求,間隔較長時也不會影響估計精度。因此,本方法對檢測數據的要求寬松,在檢測工作頻度不高、樣本數量較少的情況下仍然能較為準確地估計出裝備的壽命規律。 圖4 不同檢測間隔對平均貯存壽命仿真結果的多重箱線圖 4) 預計的壽命區間對估計精度的影響。 保持算例中其他數據不變,將預計區間分別選擇為[12,180]、[12,240]、[12,360]、[60,120]、[60,240],將分別得到的平均貯存壽命估計值,利用Matlab繪制多重箱線圖如圖5所示。由圖5可以看出,預計區間的大小對估計精度并沒有明顯影響,只要預計區間把真值包含其中即可。圖5中第四種情況下,由于預計區間[60,120]相對真值120比較偏離導致結果誤差較大。可見本方法并不要求對初始預設的壽命區間有較準確的估計,相反初設的范圍越寬(降低預計區間與真值偏離的概率),最終的結果相對越理想,這也是貝葉斯估計方法的優點之一。 圖5 不同預計區間下對平均貯存壽命仿真結果的多重箱線圖 基于對以上影響因素的分析,調整各參數的選取可實現本方法對貯存壽命更為精確的評估。如調整檢測次數m=20,樣本數N0i+N1i=30情況下,可以得出對平均貯存壽命的估計均值為121.674 2、根方差為8.190 4(如圖6所示)。 圖6 m=20, N0i+N1i=30的平均貯存壽命仿真結果的箱線圖 1) 本文提出了指數型單元件貯存壽命分布參數的貝葉斯估計方法,通過算例設計和大量仿真分析結果說明,可以在所接受的置信區間內較為準確地估計出指數型單元件的貯存壽命分布規律。 2) 本方法的好處在于估計結果受樣本規模的影響較少,且不要求對貯存壽命的初始區間給出精確的設定,相反初始區間范圍設定越寬估計結果相對越準確。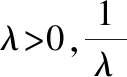
2 基于貝葉斯推斷的指數型單元貯存壽命分布參數估計模型
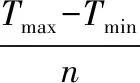
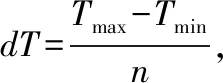
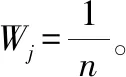

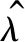
3 算例設計

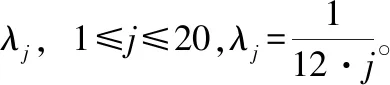


4 仿真分析
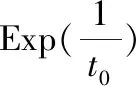




5 結論

