任憑函數多變幻 求導原則不能撼
王芝平
(北京宏志中學 100013)
函數導數綜合性問題一般都要回歸函數單調性的判斷,而判斷一個復雜函數的單調性恰是函數導數的功能之一.
解決函數導數問題一般要經歷“分析問題、構建函數、研究函數、解決問題”幾個環節.
1.分析問題 首先要弄明白我們的目的是什么?即要解決的問題是什么?它能轉化成什么等價問題(熟悉或易解決的)?
2.構建函數 為了解決上面問題,要構建恰當函數,使所構建的函數既能反映問題的本質,又更易于解決問題.
3.研究函數 一般要借助導數研究這個函數的單調性.函數導數在其零點左右兩側取值異號,那么該零點就是函數單調增、減區間的“分界點”,也必是函數極值點,進而有可能是函數的最值點.
4.解決問題 通過獲得的函數性質解決問題.
例1(2010,全國Ⅰ,理20) 已知函數f(x)=(x+1)lnx-x+1.
(Ⅰ)略;
(Ⅱ)證明:(x-1)f(x)≥0.
謀定思路有方向
利用符號法則,將(x-1)f(x)拆分為兩個函數x-1與f(x),分別研究它們的取值正負情況.這里我們返璞歸真從最直接的方法入手:欲證F(x)=(x-1)f(x)≥0成立,只需證明函數F(x)的最小值非負即可,注意到F(1)=0,我們可以猜測F(x)的最小值為F(1),即F(x)在區間(0,1]上是減函數,而在區間[1,+∞)上是增函數,也就是F′(x)的值以1為“界”“先負后正”.這個想法可以反復使用,讓我們試一試吧!
規范解答不失分
(Ⅱ)解 令F(x)= (x-1)f(x)(x>0),
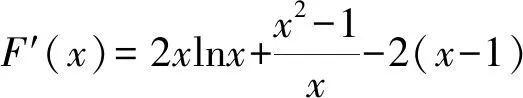
因為F′(1)=0,所以F′(x)如果是增函數,那么我們的“小目標”就會得以實現.“函數單調不單調,導數正負破玄妙”,讓我們看看函數F′(x)的導數的是正的還是負的吧!
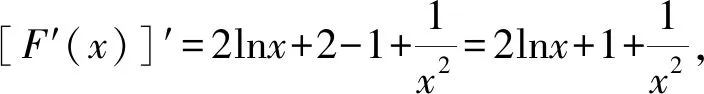
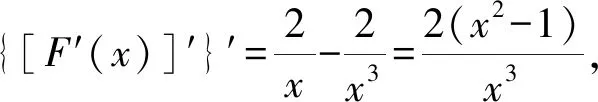
所以{[F′(x)]′}′>0?x>1,
{[F′(x)]′}′<0?0 所以[F′(x)]′在區間(0,1]上是減函數, 而在區間[1,+∞)上是增函數. 所以[F′(x)]′≥[F′(1)]′=2>0, 所以F′(x)是增函數. 因為F′(1)=0, 所以F′(x)>0?x>1,F′(x)<0?0 所以F(x)在區間(0,1]上是減函數, 而在區間[1,+∞)上是增函數. 所以F(x)≥F(1)=0, 即(x-1)f(x)≥0恒成立. 上述過程雖然艱難曲折,但是對導數的功能卻有了更深層次的切身感悟,讓我們充分體會到“任憑函數多變幻,求導原則不能撼——函數單調不單調,導數正負破玄妙”,簡單地說,如果想知道一個函數的單調性,那么就看看其導數的正負吧! 可謂“不忘初心,方得始終”! 例2(2018,全國Ⅲ,理21) 已知函數f(x)=(2+x+ax2)ln(1+x)-2x. (Ⅰ)若a=0,證明:當-1 (Ⅱ)若x=0是f(x)的極大值點,求a. 解(網上流傳的官方答案) 當-1 當x>0時,g′(x)>0. 故當x>-1時,g(x)≥g(0)=0, 且僅當x=0時,g(x)=0, 從而f′(x)≥0,且僅當x=0時, f′(x)=0.所以f(x)在(-1,+∞)單調遞增. 又f(0)=0,故當-1 f(x)<0;當x>0時,f(x)>0. (2)(i)若a≥0,由(1)知,當x>0時,f(x)≥(2+x)ln(1+x)-2x>0=f(0),這與x=0是f(x)的極大值點矛盾. 故h(x)與f(x)符號相同. 又h(0)=f(0)=0, 故x=0是f(x)的極大值點當且僅當x=0是h(x)的極大值點. h′(x)>0,故x=0不是h(x)的極大值點. 所以x=0不是h(x)的極大值點. 如果6a+1=0, 則當x∈(-1,0)時,h′(x)>0; 當x∈(0,1)時,h′(x)<0. 所以x=0是h(x)的極大值點, 從而x=0是f(x)的極大值點. 下面給出我們的分析與解法. (Ⅰ)易知f(0)=0,由結論可知,只需證明a=0時f(x)是增函數即可,進而考察f′(x)是否恒不小于0.如果不易發現f′(x)的正負,可繼續討論函數f′(x)的導函數取值情況,這個過程可反復進行. (Ⅱ) 因為x=0是f(x)的極大值點,又f(x)是可導函數,由極值點的定義及極值點與函數導數的關系可知,f′(0)=0且f′(x)在x=0的左右兩側的取值符號應該是“左正、右負”,所以f′(x)在以0為中心的一個區間(如(-b,b))上是減函數.這就要繼續研究f′(x)的導函數[f′(x)]′是否小于0,如果不達目的,可如法炮制繼續研究[f′(x)]′的導函數. 也可以綜合利用“復雜函數大于零,符號法則立奇功”與“不等結構任紛雜,適當分離變通達”等策略,將函數f(x)轉化為較為簡單的函數予以研究. 規范解答不失分 解(Ⅰ)函數f(x)的定義域為 (-1,+∞) . 當a=0時,f(x)=(2+x)ln(1+x)-2x, 當-1 當x>0時,g′(x)>0. 故當x>-1時,g(x) ≥g(0) =0, 且僅當x=0時,g(x)=0, 所以g(x)=f′(x)在區間(-1,0)上是減函數, 在區間(0,+∞) 上是增函數, 從而f′(x)≥f′(0)=0, 且僅當x=0時,f′(x)=0. 所以f(x)在(-1,+∞)單調遞增. 又f(0)=0,故當-1 f(x)<0;當x>0時,f(x)>0 (Ⅱ)方法1 (i)若a≥0,由(1)知,當x>0時,f(x)≥(2+x)ln(1+x)-2x>0,這與x=0是f(x)的極大值點矛盾. 因為若x=0是f(x)的極大值點, 所以f′(x)在x=0的左右兩側的取值符號應該是“左正、右負”, 所以f′(x)在以0為中心的一個區間上是減函數. 這就要再研究f′(x)的導數, 我們希望[f′(x)]′<0, 那么x=0是[f′(x)]′的極大值點. 同理{[f′(x)]′}′在x=0處的導數等于0,且在x=0左右兩側的取值符號應該是“左正、右負”, 所以,當-1 當0 即當-1 當且僅當x=0時,[f′(x)]′=0. 所以f′(x)在區間(-1,1)上是減函數. 又因為f′(0)=0, 所以當-1 當0 所以f(x)在區間(-1,0)上是增函數,在區間(0,1)上是減函數, 所以x=0是f(x)的極大值點,該極大值為f(0)=0. (Ⅱ)方法2 (i)若a≥0,由(1)知,當x>0時,f(x)≥(2+x)ln(1+x)-2x>0,這與x=0是f(x)的極大值點矛盾. (ii)若a<0,注意到函數f(x)的復雜性,可將2+x+ax2與ln(1+x)進行“分離”. 先研究函數r(x)=2+x+ax2的一些基本特征: 因為a<0,所以二次函數r(x)的圖像開口向下, 又Δ=4-8a>0,r(0)=2>0, 所以存在一個區間(-b,b)(0 在這個區間上r(x)>0, 因為f(x) =(2+x+ax2)ln(1+x)-2x 因為x=0是f(x)的極大值點, 即f(x)≤f(0)=0, 又h(0)=0, 所以“x=0是f(x)的極大值點”等價于“x=0是h(x)的極大值點”. 這等價于h(x)在(-b,0)上是增函數, 在(0,b)上是減函數, 即在(-b,0)上,h′(x)>0, 在(0,b)上h′(x)<0,且h′(0)=0. 令p(x)=a2x2+4ax+6a+1 (-b 則x=0不是h(x)的極大值點. 即若x=0是h(x)的極大值點, (必要條件) 所以h′(x)>0?p(x)>0?-b 所以h(x)在區間(-b,0)上是增函數,在區間(0,b)上是減函數, 所以x=0是h(x)的極大值點, 即x=0是f(x)的極大值點. (充分條件) 利用導數研究函數性質時,要明白求導的目的與意義是什么?不能讓求導成為一種僵化的解題模式,求導之后就不知道干什么了,這歸根結底還是沒有從本質上理解導數工具能為我們分析函數帶來什么.上面的解法不同于標準答案,其特點是不斷分析新的目標函數應該正負如何,單調性如何,指引的非常清晰,解題很有目標感.這就是所謂的“發現問題、提出問題、分析問題、解決問題”的能力吧. 在上述解法中,雖然多次構造新的函數、多次求導,但是它們都不是解決問題的本質核心,核心是我們想研究函數的什么,我們用什么工具手段來研究,從這點來說,三次求導雖然罕見,但是并不是新鮮的題型,而是對于“原則”的合理運用,“任憑函數多變幻,導數原則不能撼”正是一針見血的點明了這一點. 再次表明我們的態度:“任憑函數多變幻,求導原則不能撼——函數單調不單調,導數正負破玄妙”.解后反思要升華
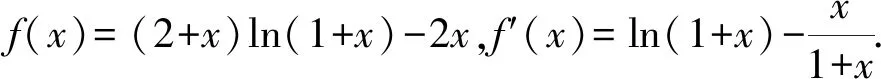
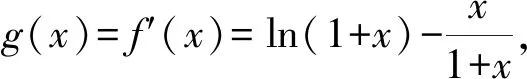
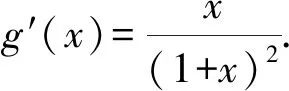
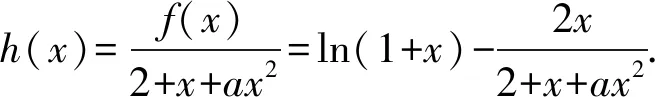
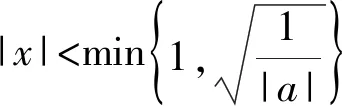
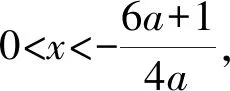
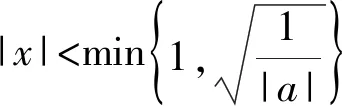
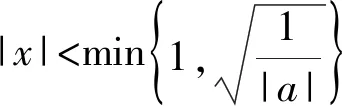
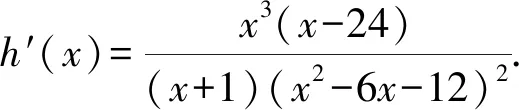
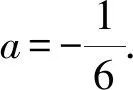
謀定思路有方向
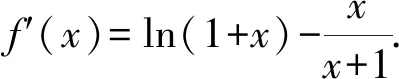

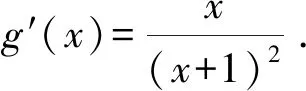
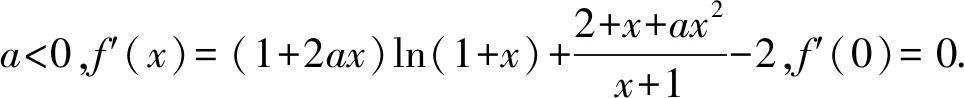
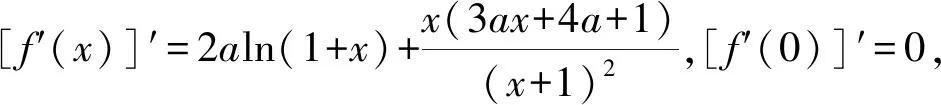
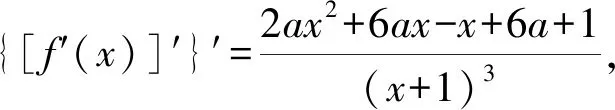
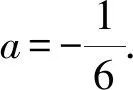
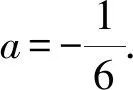
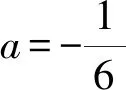
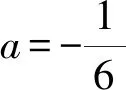
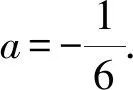
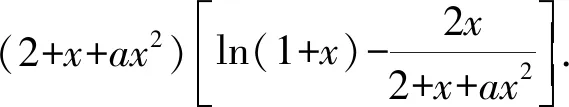
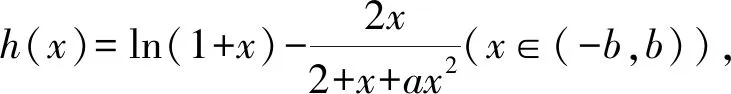
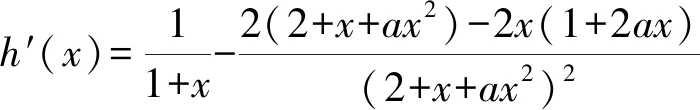
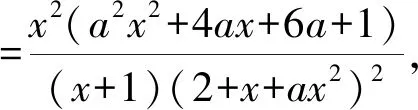
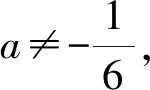
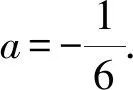
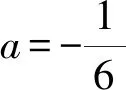
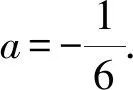
解后反思要升華

