考慮不同堆載過程的棄渣場穩(wěn)定性分析

楊建強

(中鐵十七局集團建筑工程有限公司，太原 030006)

鐵路、公路建設是線形工程，沿線地形復雜多樣，施工過程中經常高挖低填，會產生大量土石方棄渣。棄渣體隨意堆置且施工過程中往往防護不當，對生態(tài)環(huán)境產生嚴重破壞，導致水土流失。因此，妥善處置工程建設期間產生的棄渣剝離體十分重要。棄渣場作為工程建設的副產物，是伴隨著工程施工而形成的一種巨大的人工松散堆積體。棄渣場所堆放的棄渣體屬于松散介質，工程性能差，邊坡抗滑能力差，降雨易入滲，其物理性質介于固體和液體之間。分析掌握棄渣場的穩(wěn)定狀態(tài)，對于工程的正常施工建設及運營十分關鍵。

國際上關于棄渣場邊坡穩(wěn)定性及其防治措施的研究始于20世紀70年代[1-2]。近年來，國內外學者從不同角度對渣場邊坡穩(wěn)定性進行了分析。吳謙等以某鐵路隧道為例，基于Monte Carlo算法，分析了棄渣場邊坡穩(wěn)定系數對各項計算參數的敏感性，得到了棄渣內摩擦角φ、黏聚力及重度變化對渣場邊坡穩(wěn)定系數的影響程度[3]。陳武等學者基于滲流理論對渣場穩(wěn)定性進行了數值模擬分析計算，得到了降雨對渣場穩(wěn)定性的影響[4-6]。保華富等對棄渣場邊坡的變形范圍及可能失穩(wěn)區(qū)域分別進行監(jiān)測，從而探尋邊坡的變形特性、破壞機理。這些研究雖然考慮了降水及渣場計算參數變化等因素對渣場穩(wěn)定性的影響，但未能反映棄渣場的動態(tài)堆載過程[7]。

本文以山西省某工程棄渣場為例，利用有限元軟件Midas GTS對棄渣場的變形和應力特征進行數值分析，研究棄渣場內部的應力大小及分布、位移大小及分布規(guī)律，探討在動態(tài)堆載過程下，分析不同分步堆載情況下棄渣場的變形和穩(wěn)定性變化情況。

1 棄渣場堆積體模型及參數選擇

以山西省某工程棄渣場為例，利用有限元軟件Midas GTS對棄渣場的變形和應力特征進行有限元分析。棄渣場邊坡分析模型見圖1。

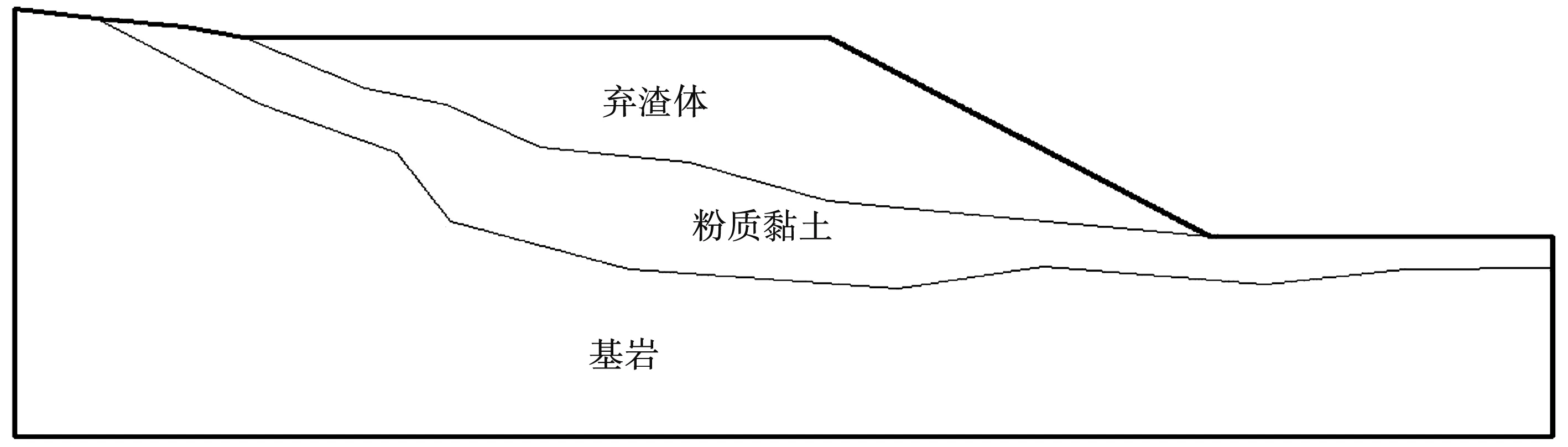
圖1 棄渣場邊坡分析模型

考慮棄渣場堆積體的彈塑性特點，本文本構模型采用Mohr-Coulomb屈服準則進行相應模擬分析。Mohr-Coulomb塑性模型的參數具有簡單且能較好反映土體的彈塑力學特性的特點。

其屈服函數為[8-9]：

(1)

(2)

式中：I1為應力張量第一應力不變量，I1=σx+σy+σz；θσ為洛德角，-30°≤θσ≤30°；J2為應力偏張量的第二不變量。

采用有限元計算是否收斂作為評價標準，計算得出的折減系數即為安全系數。安全系數取值及邊坡穩(wěn)定性狀態(tài)，參考《建筑邊坡工程技術規(guī)范》(GB 50330-2013)進行選取。

該工程典型棄土場堆渣體力學參數見表1。為便于建模分析計算，對每一土層的計算參數取特定值。

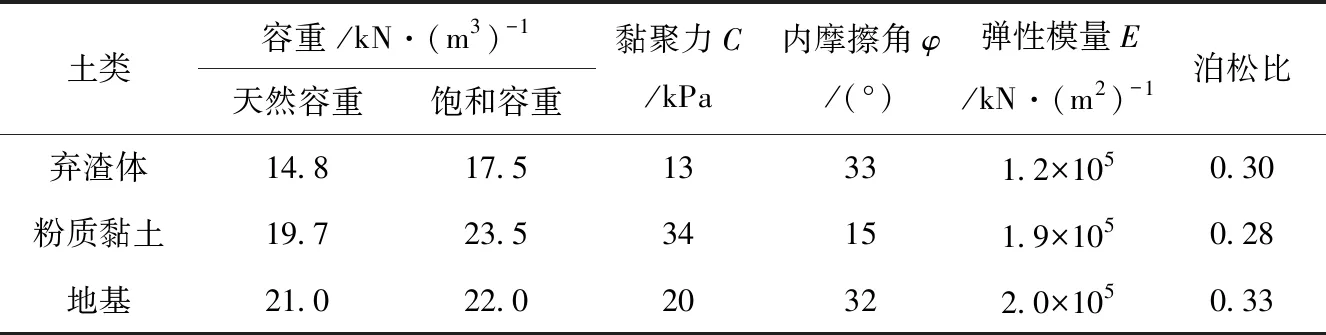
表1 棄渣場堆渣體計算參數

2 棄渣場的穩(wěn)定性分析

根據有限元法的計算要求對棄渣場模型的計算區(qū)域進行網格劃分，劃分網格時選用循環(huán)網格化四邊形網格，并根據強度折減法要求，生成中間節(jié)點。將棄渣場堆積體進行模型網格劃分，劃分為1 094個單元，共1 166個節(jié)點，見圖2。理論上劃分的網格越密計算結果越精確，但會導致計算量的增加。因此在計算時，對棄渣堆積體及坡面邊坡的網格劃分進行適當的加密處理。

堆積體坡頂以及坡面邊界網格尺寸為4 m，基巖和粉質黏土全部邊界和堆積體底邊界網格尺寸為8 m。計算得到自重作用下棄渣場邊坡位移云圖和剪切應變云圖，見圖3、圖4。其最大、最小主應力主要體現棄渣體的拉壓狀態(tài)，位移云圖和剪切應變圖可用來判斷棄渣場邊坡的失穩(wěn)區(qū)域，根據塑性區(qū)的情況可判斷其渣場邊坡是否發(fā)生整體性失穩(wěn)破壞。

圖2 棄渣場邊坡分析模型網格劃分圖

圖3 棄渣場邊坡位移云圖

圖4 棄渣場邊坡剪切應變云圖

通過數值模擬計算，得到此模型中棄渣場堆積體在重力作用下整體穩(wěn)定性系數為1.225。邊坡最大位移為0.302 m，邊坡位移變形主要集中在下部，在棄渣場坡腳處有局部破壞趨勢。

3 分步堆載過程中渣場的變形演變

為更好地反映棄渣場建設過程中棄渣體的堆置對邊坡穩(wěn)定性的影響，將該棄渣場按不同堆置步驟分為壓坡腳式(順排)和覆蓋式(逆排)兩種堆置步驟，并對不同堆載步驟的棄渣場模型進行邊坡穩(wěn)定性分析。

3.1 分步堆載模型

棄渣場的分步堆載分析模型建立在原棄渣場邊坡分析模型(圖1)的基礎上，考慮堆載步驟的不同，建立順排堆載和逆排堆載兩種分析模型，見圖5。

3.2 堆載過程變形演變規(guī)律

對棄渣場逐步堆載過程進行建模運行計算，在考慮自重作用的情況下，分析其每一個堆載步驟在施工過程中對邊坡穩(wěn)定性系數、位移變化以及剪切應變的影響，并分析棄渣場在堆載過程中的演變規(guī)律。

圖5 不同堆置步驟分析模型圖

3.2.1 壓坡腳式堆載過程的變形演變

對壓坡腳式堆載方式進行加載計算，計算結果見圖6及表2。從計算結果來看，壓坡腳式(順排)堆置方式在堆載過程中，其穩(wěn)定性系數在1.221～1.331之間，在自重作用下處于基本穩(wěn)定狀態(tài)。棄渣場最大位移出現在第一步堆載后，數值為31.2 cm左右，之后位移變化呈較緩的遞減趨勢，變化范圍在0～0.033 m之間。第三步堆載后呈現出最大剪切應變?yōu)?.751，隨著每一個堆載步驟下的渣體對前一步驟堆置的渣體的反壓作用，其塑性區(qū)域逐漸縮小收斂，壓坡腳式堆置方式的可能剪出口始終位于坡腳位置，且隨最終堆置線坡腳位置的改變而改變。云圖中相鄰步驟變化趨勢相近的將不單獨列圖，相近兩步或多步則取其最后一步為示意圖，下文中不再說明。

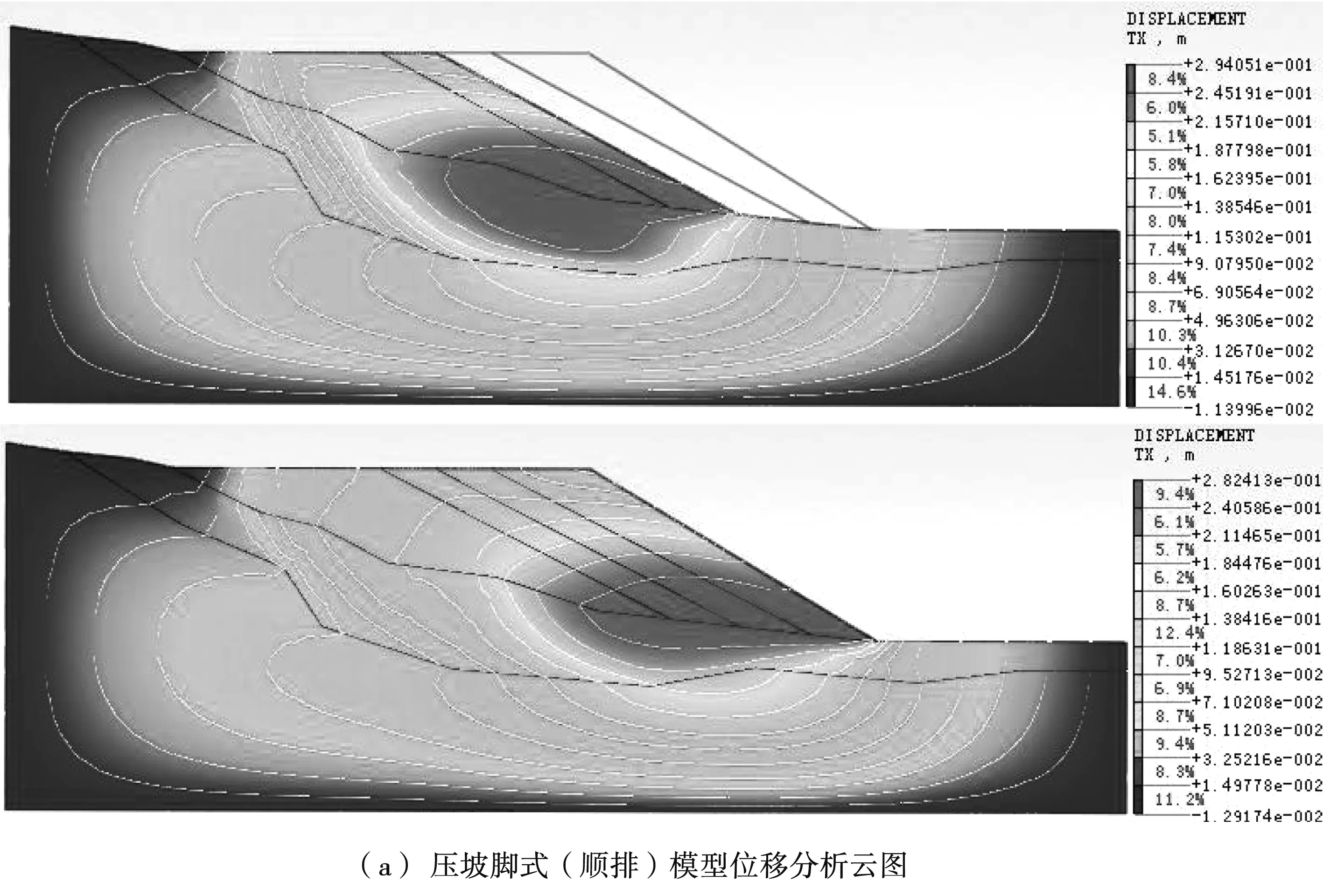
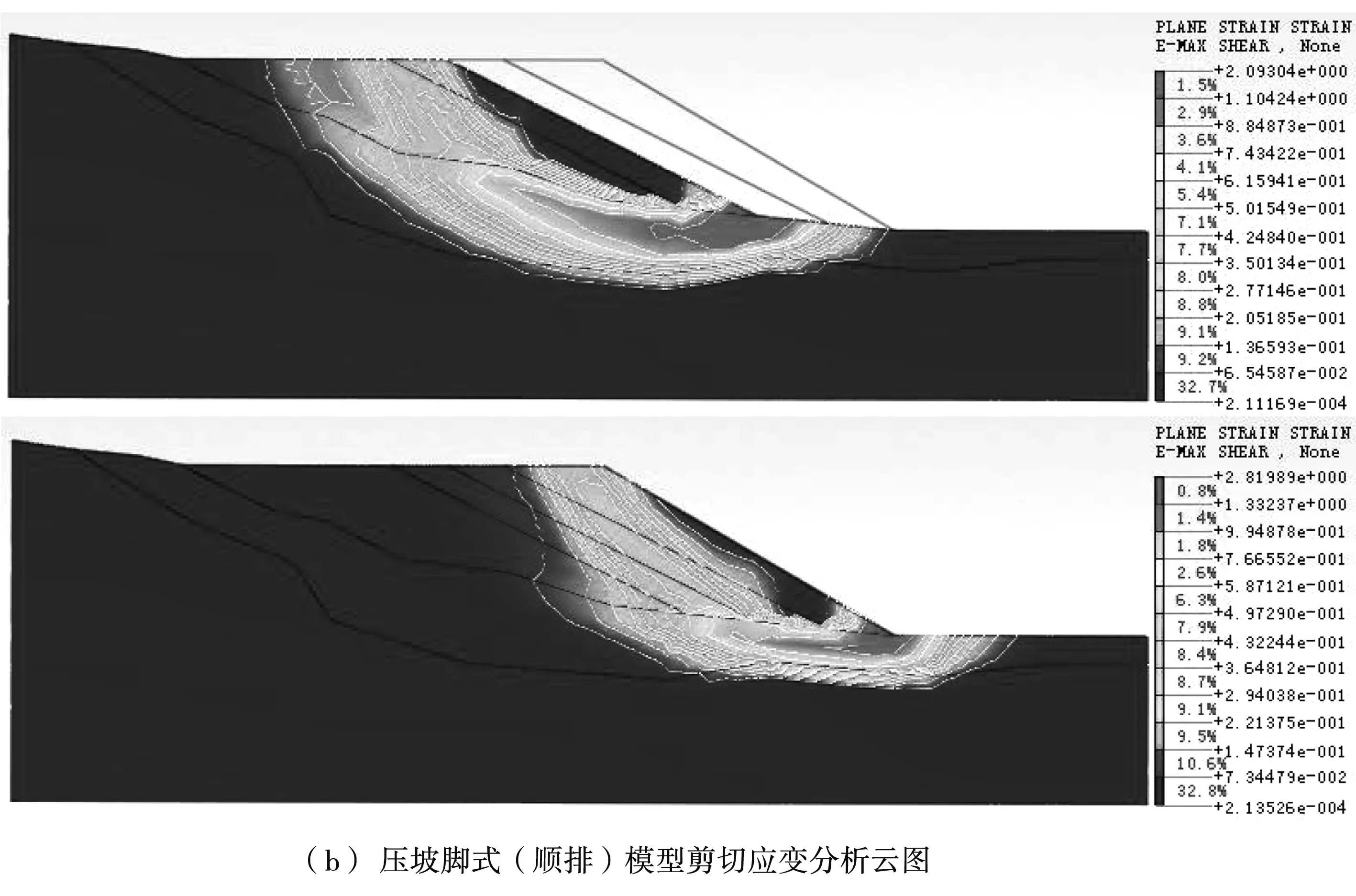
圖6 壓坡腳式堆載過程分析

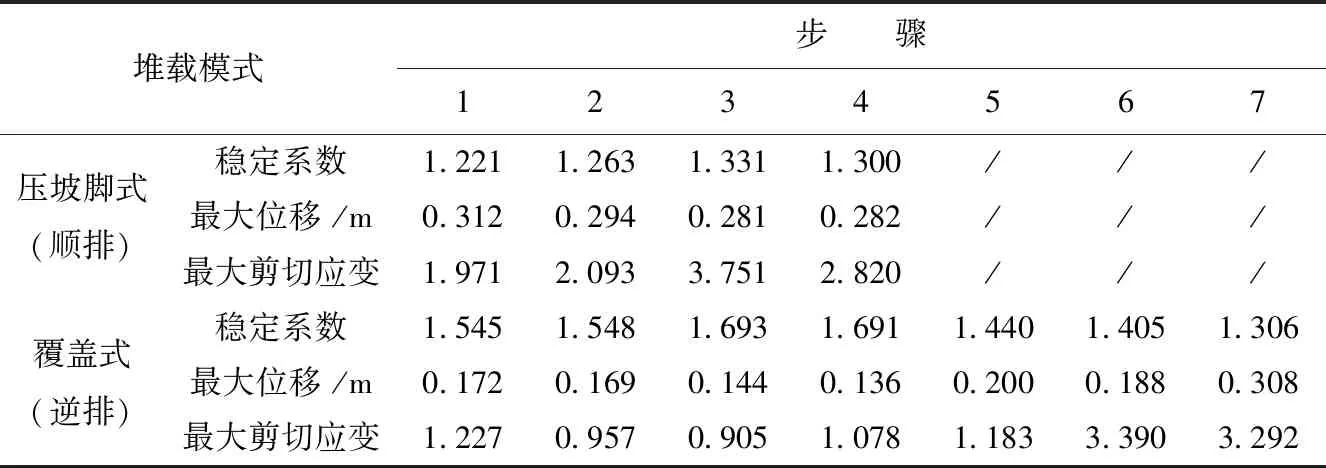
表2 棄渣場堆載過程參數變化值

3.2.2 覆蓋式堆載過程的變形演變

同理，對覆蓋式(逆排)堆置進行加載計算，計算結果見圖7及表2。覆蓋式(逆排)堆置方式在堆載過程中穩(wěn)定性系數在1.306～1.693之間，在自重作用下處于穩(wěn)定狀態(tài)。棄渣體堆置完后體現出最大位移為30.8 cm，位移隨著堆載步驟的推進呈遞增趨勢，第三步和第四步堆載過程中最大位移變化出現分散集中現象。整個堆載基本完成時出現最大應變3.390，堆載過程中塑性區(qū)由邊坡上部逐漸向中部再向下部移動，在堆載徹底完成時塑性變形區(qū)完全收斂于坡腳。

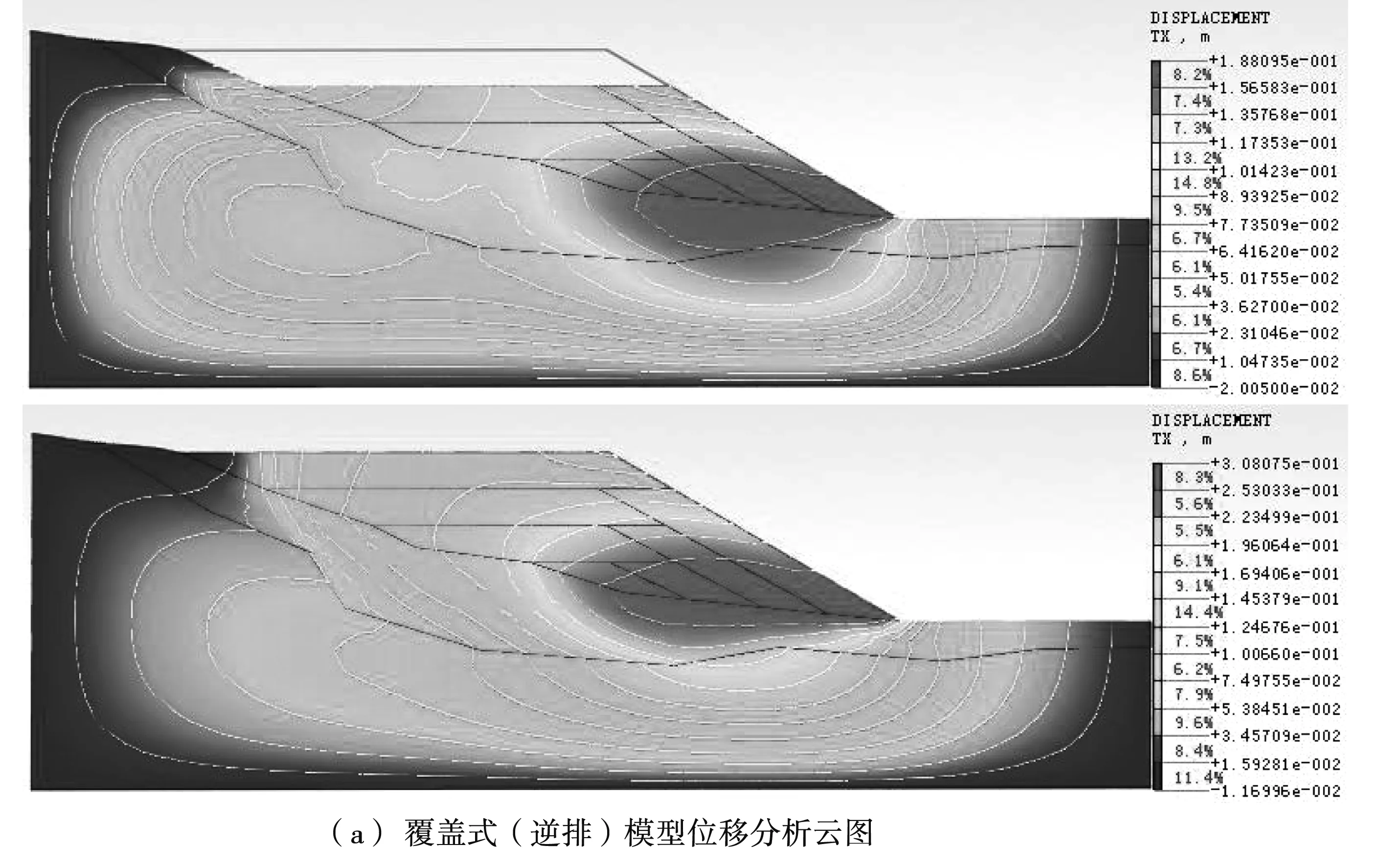
圖7 覆蓋式堆載過程分析

由表2可知，在堆置過程中，覆蓋式棄渣場的平均穩(wěn)定系數為1.518，高于壓坡腳式棄渣場的平均穩(wěn)定系數1.278，對棄渣場邊坡的穩(wěn)定性提高更有益，提高率為18.73%。在棄渣場邊坡穩(wěn)定性更好的前提下，覆蓋式的最大位移平均值和最大應變平均值均小于壓坡腳式。

運用Midas GTS模擬計算棄渣場堆載渣體前原始邊坡穩(wěn)定系數，得到原始值為1.54。從表2可以看出，無論渣體的堆置采用壓坡腳式還是覆蓋式，對邊坡整體穩(wěn)定性都呈削弱趨勢，但邊坡依舊穩(wěn)定。同時，也可發(fā)現覆蓋式堆載方式對邊坡穩(wěn)定性的削弱作用遠小于壓坡腳式，由此可知覆蓋式堆載方式較壓坡腳式更利于保證棄渣場邊坡的穩(wěn)定。

4 結 論

1) 以山西省某工程棄渣場為例，建立棄渣場有限元分析模型，分析棄渣場整體穩(wěn)定性及考慮不同堆載過程的渣場穩(wěn)定性變化情況。

2) 從渣場整體穩(wěn)定性分析可知，邊坡位移變形主要集中在邊坡下部，在棄渣場坡腳處有局部破壞趨勢。

3) 考慮分步堆載過程演變，根據堆載順序不同，分為壓坡腳式(順排)和覆蓋式(逆排)堆置，無論渣體的堆置采用哪種方式，對邊坡整體穩(wěn)定性均呈削弱趨勢。

4) 棄渣場安全系數、位移、應變的變化隨堆載過程不同而有所區(qū)別，覆蓋式的最大位移平均值和最大應變平均值均小于壓坡腳式。從最終穩(wěn)定性來看，覆蓋式堆載優(yōu)于壓坡腳式堆載。