無蝸殼風(fēng)機箱優(yōu)化設(shè)計

吳 飛，吳振宇，張 虎

(武漢理工大學(xué) 機電工程學(xué)院，湖北 武漢 430070)

無蝸殼離心風(fēng)機由于有占用空間小，安裝方便，出風(fēng)方向任意，無“喘振”現(xiàn)象等優(yōu)點，在通風(fēng)、空調(diào)和消防等設(shè)備中快速發(fā)展和普及，但是風(fēng)機效率達不到75%的平均水平，而且相對于傳統(tǒng)離心風(fēng)機，出口靜壓不足，難以承擔(dān)足夠的管網(wǎng)阻力。隨著近年來通風(fēng)空調(diào)系統(tǒng)及風(fēng)機部分向高效率、小體積、安裝方便等方向發(fā)展,無蝸殼風(fēng)機的研究漸有起色，如對無蝸殼風(fēng)機箱在結(jié)構(gòu)尺寸、壓力和噪聲等方面的優(yōu)缺點進行系統(tǒng)研究[1-2], 得出無蝸殼風(fēng)機是體積和噪聲為風(fēng)機選用的主要考慮因素下的首要選擇；針對葉輪和葉片氣動特性的分析和優(yōu)化設(shè)計[3-4]以等熵效率極大為目標(biāo)，保證流量和總壓比不變的情況下進行優(yōu)化；針對葉輪與蝸殼徑向相對位置[5]和多個風(fēng)機性能參數(shù)[6-8]的優(yōu)化設(shè)計等，采用變參數(shù)的方法尋找蝸舌過渡半徑與噪聲的關(guān)系，比較不同方案的優(yōu)化效果并進行挑選。綜上所述，風(fēng)機的優(yōu)化設(shè)計涉及到風(fēng)機的各個組件和性能參數(shù)，試驗設(shè)計和優(yōu)化算法。選取合適的優(yōu)化目標(biāo)和優(yōu)化變量是研究者需要考慮的重要問題。

無蝸殼風(fēng)機箱主要結(jié)構(gòu)有集流器、葉輪和箱體。風(fēng)機箱箱體是無蝸殼風(fēng)機箱區(qū)別于一般無蝸殼風(fēng)機的特點，鈑金箱體的加工也比較容易實現(xiàn)，更重要的是，箱體的尺寸參數(shù)相對少且相互獨立，因此將箱體尺寸作為變量進行優(yōu)化設(shè)計。

1 風(fēng)機箱仿真計算與驗證

1.1 風(fēng)機箱物理模型和性能參數(shù)

風(fēng)機箱整體模型和連接結(jié)構(gòu)如圖1所示，由于加工誤差和裝配調(diào)整，實際位置和設(shè)計尺寸有一定的偏差，重要尺寸如葉輪位置，葉輪前盤和集流器之間的縫隙寬度等，需要校驗驗證；簡化實體模型，忽略葉片和葉輪前后盤之間的焊接痕跡和縫隙，視焊接連接為一體；省略工藝倒角和折彎圓角；簡化風(fēng)機箱箱體的支撐結(jié)構(gòu)，制作為一個整體；將連接電機主軸和葉輪后盤軸法蘭的復(fù)雜結(jié)構(gòu)簡化為一體。簡化對應(yīng)的空間模型，有利于網(wǎng)格劃分。

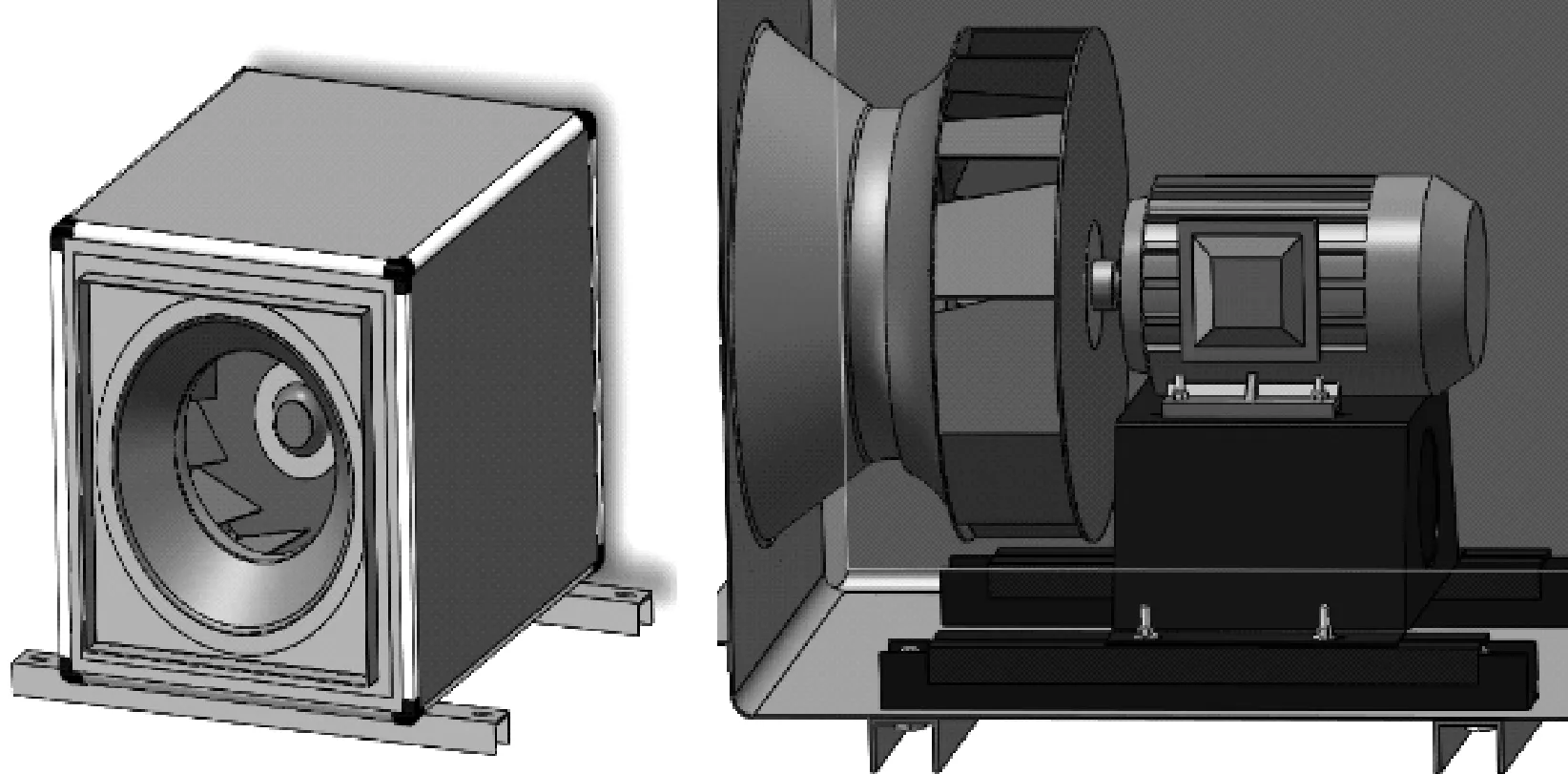
圖1 整體模型和連接結(jié)構(gòu)

無蝸殼風(fēng)機箱主要性能參數(shù)有流量、壓力、轉(zhuǎn)速、功率和效率,風(fēng)機進、出口截面全壓數(shù)值的代數(shù)差為風(fēng)機的全壓Ptq；無蝸殼風(fēng)機管克服管網(wǎng)阻力所需的壓力，即風(fēng)機箱通產(chǎn)生的全壓去除出口動壓的剩余部分為風(fēng)機的靜壓Ptst。

采用軸向送風(fēng)的無蝸殼風(fēng)機箱，氣體首先在葉輪的作用下獲得能量，即靜壓和部分動壓；然后，氣體離開葉輪進入箱體，在箱體中體積驟增，靜壓驟減，一部分靜壓轉(zhuǎn)化為動壓；最后，氣體和壁面正碰撞，部分動壓完全損失而沒有轉(zhuǎn)化為靜壓。

全壓效率η為通風(fēng)機有效功率N和軸功率N2的比值，用于衡量風(fēng)機氣動性能。其計算公式為：

η=NN2=NN1·N1N2=ηi·ηm

(1)

式中：ηi為內(nèi)效率;ηm為傳動功率；N1為內(nèi)功率。

當(dāng)管網(wǎng)工況達到大流量區(qū)時，風(fēng)機提供的能量大多轉(zhuǎn)化為氣體動能，造成靜壓不足以克服管網(wǎng)阻力。為了考量上述情況，提出了靜壓效率的概念，其計算公式如下：

ηst=PτstPtqη

(2)

1.2 仿真計算與試驗驗證

使用ICEM制作網(wǎng)格，網(wǎng)格的節(jié)點數(shù)目為795 847，網(wǎng)格數(shù)目為2 254 785。網(wǎng)格的偏斜率在0.85以下，網(wǎng)格質(zhì)量總體大于0.8，長寬比、翹曲因數(shù)等適中。

對流場和靜壓進行定常模擬[9]，壓力入口設(shè)置為大氣壓；質(zhì)量流出口按照不同工況將流量按照1.225 kg/m3換算為kg/s的質(zhì)量流。采用SIMPLEC (SIMPLE-consistent)算法[10]對噪聲進行非定常模擬，算法上選用PISO，計算格式上選用有界二階隱式。仿真結(jié)果如表1所示。

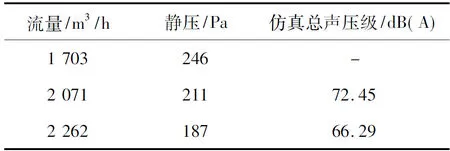
表1 仿真結(jié)果

流量壓力測試根據(jù)風(fēng)機氣動測試試驗標(biāo)準(zhǔn)GB/T1236-2000選C型進口側(cè)風(fēng)道進行，通風(fēng)機的噪聲測試依據(jù)通用設(shè)備的噪聲源測定標(biāo)準(zhǔn)。試驗數(shù)據(jù)、仿真數(shù)據(jù)和出廠全壓數(shù)據(jù)如表2所示，從表2可知，流量-壓力仿真結(jié)果在趨勢上是基本正確的，即仿真的數(shù)據(jù)和方法可以用來指導(dǎo)下一步的優(yōu)化設(shè)計與改造。

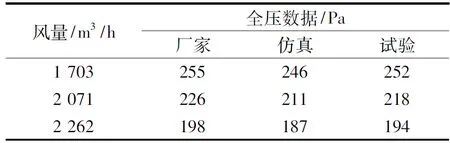
表2 試驗/仿真/出廠全壓數(shù)據(jù)對照

2 針對風(fēng)機效率和噪聲的風(fēng)機箱尺寸優(yōu)化

基于模型進行試驗設(shè)計。響應(yīng)面法(response surface methodology,RSM)采用析因設(shè)計的思路，對設(shè)計目標(biāo)(響應(yīng))受到多個設(shè)計變量影響的問題進行建模和分析。

響應(yīng)面法采用多元二次多項式來近似擬合設(shè)計變量和響應(yīng)變量之間的真實函數(shù)關(guān)系。設(shè)實際的真實函數(shù)為y，響應(yīng)面模型產(chǎn)生的函數(shù)為y0,其相互關(guān)系為：

y=y0+λ

(3)

式中：λ為模型誤差；響應(yīng)面產(chǎn)生的函數(shù)模型y0為多元二次多項式：

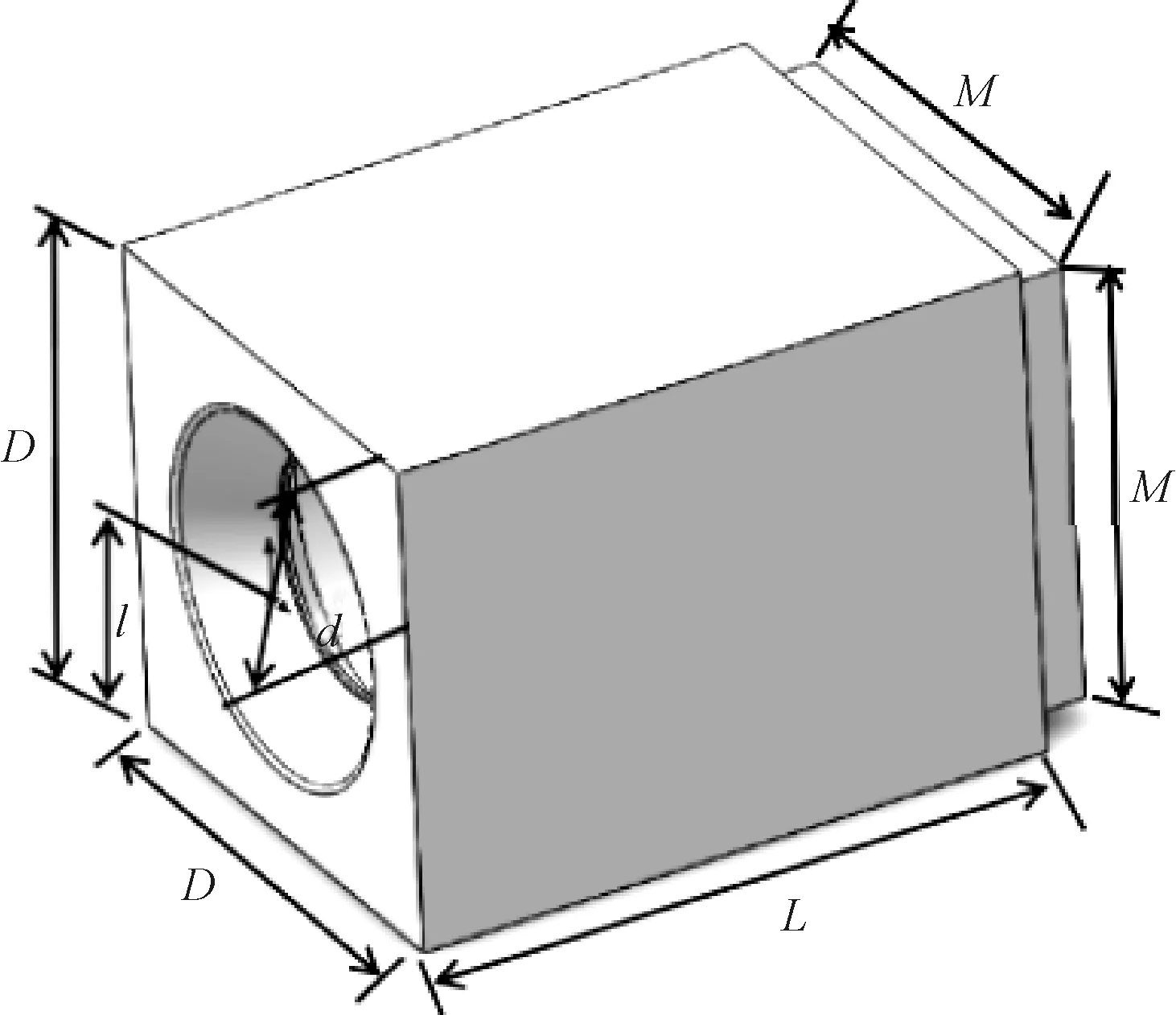
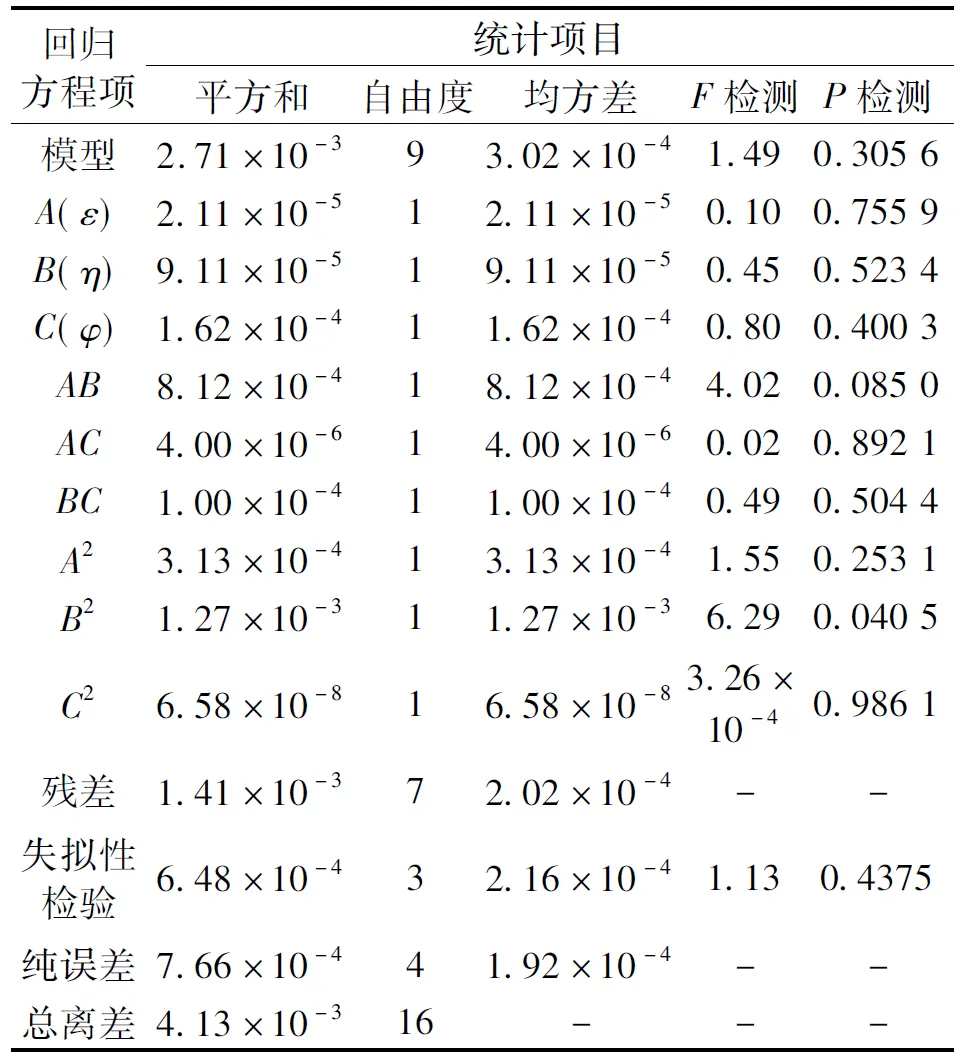
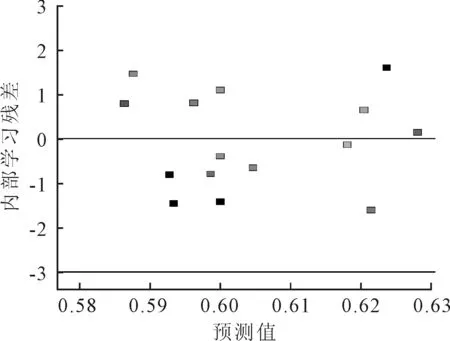
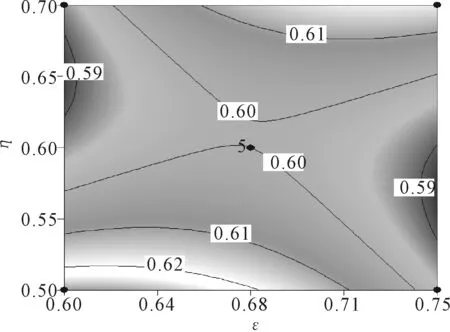
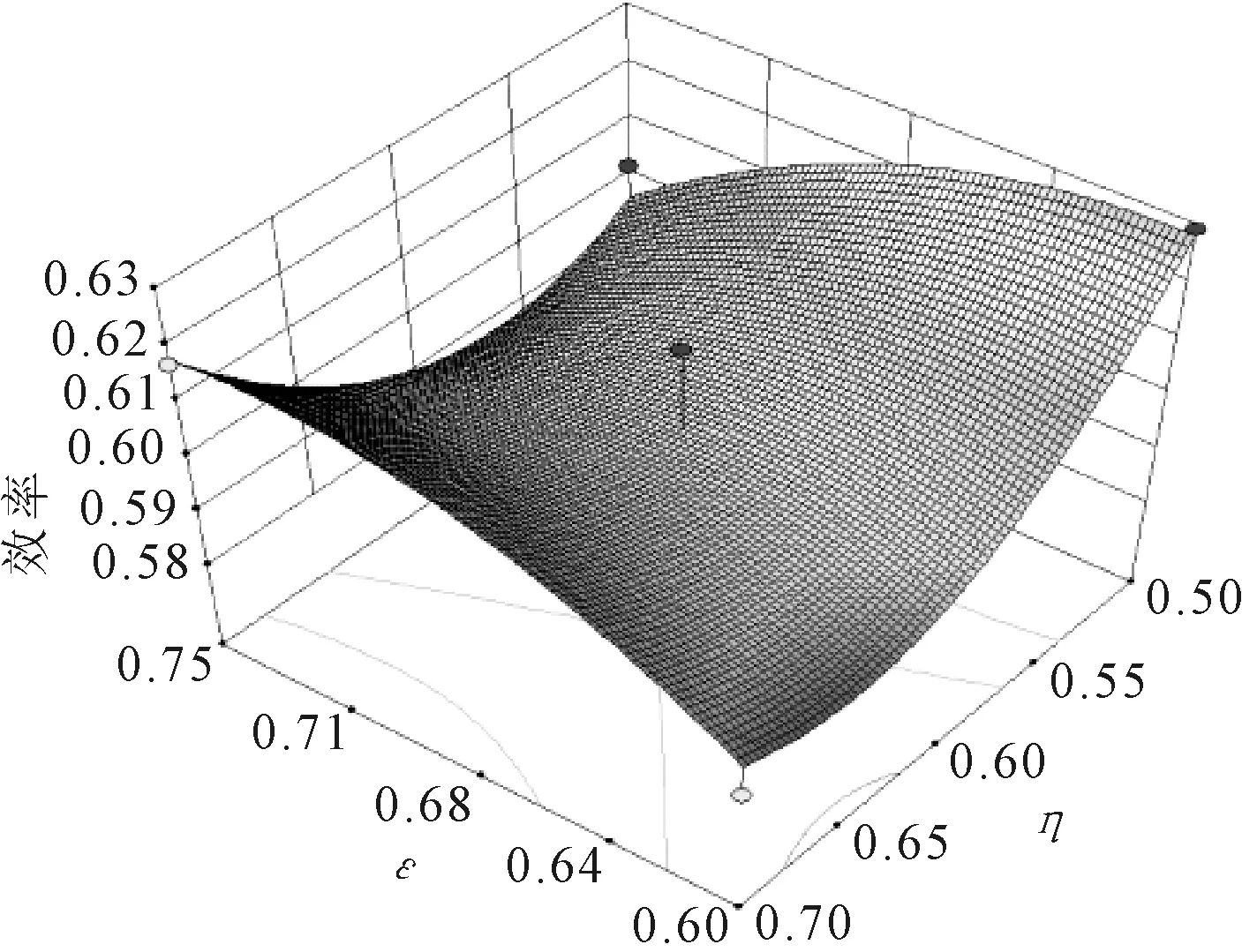
y0=a+∑mj=1bjxj+∑k

(4)

式中：k=1,2，…,m-1(j≠k)；x為各影響因子；bj為xj的線性效應(yīng)；bkj為xk與xj之間的線性交互關(guān)系；bjj為xj的二次效應(yīng)。

通過試驗設(shè)計，獲得一系列的樣本點，將樣本點進行回歸，建立響應(yīng)面方程。然后，對回歸方程進行顯著性檢驗。最后，通過繪制響應(yīng)面或者等高線圖預(yù)測最佳數(shù)值。回歸中，為保證響應(yīng)變量在取最佳的設(shè)計變量時落在試驗范圍之內(nèi)，還需要多次試驗來確定設(shè)計變量的所在范圍。

2.1 參數(shù)選擇與試驗設(shè)計

風(fēng)機箱的橫截面尺寸為D×D，出風(fēng)口截面尺寸為M×M，長度為L，葉輪中心到地面的距離為l，葉輪直徑為d(已知)。如圖2所示，綜合設(shè)計和實測尺寸可得原設(shè)計的各個變量值為：d=355 mm，L=660 mm，D=540 mm，M=460 mm，l=270 mm。

圖2 風(fēng)機箱體的基本參數(shù)

通過響應(yīng)面法，研究葉輪直徑和箱體橫截面尺寸比值ε；葉輪直徑和箱體長度尺寸比值η；葉輪直徑和出風(fēng)口橫截面尺寸比值φ，這3個變量對風(fēng)機性能和氣動噪聲的影響。

ε=dD,η=dL,φ=dM

(5)

原設(shè)計的3組變量數(shù)值為：ε=0.657 4，η=0.538，φ=0.772。初步選定ε的范圍是0.60～0.75，η的范圍是0.5～0.7，φ的范圍是0.75～0.90。同時出口截面的尺寸εmax必然小于箱體截面的尺寸φmax；箱體的長度至少要包括整個電機，即ηmax≤355/495=0.71。

優(yōu)化設(shè)計的目標(biāo)函數(shù)為風(fēng)機靜壓效率和噪聲。試驗設(shè)計是三因素(ε，η，φ)和三水平(-1、0、1)。

使用design-expert軟件生成列表，試驗次數(shù)為17組。然后將每次試驗的參數(shù)帶入式(3)中求得該次試驗的模型尺寸，并對原始空間模型進行修改，產(chǎn)生17個新模型。再按照數(shù)值模擬的流程將新模型逐次導(dǎo)入Fluent中進行仿真分析，仿真的項目為風(fēng)機的靜壓、總壓和噪聲，然后根據(jù)式(1)和式(2)計算全壓效率和靜壓效率。所得仿真數(shù)據(jù)統(tǒng)計結(jié)果如表3所示。

表3 仿真數(shù)據(jù)統(tǒng)計結(jié)果

2.2 回歸方程的建立與診斷

將表3中的靜壓效率寫入到design-export中，尋找并擬合與箱體尺寸3個變量ε、η、φ之間的函數(shù)關(guān)系。其中，統(tǒng)計變換采用默認(rèn)(無方程，經(jīng)典響應(yīng))，擬合模型采用二次多項式，結(jié)果如表4所示。

表4 二階方差分析表

模型的F檢測數(shù)值為1.49，表明模型與噪聲這一響應(yīng)沒有必然關(guān)系，并且有30.56%的可能性在該項中出現(xiàn)如此大的數(shù)值。P檢測的數(shù)值表明，B2項在模型中顯著。一般當(dāng)P值小于0.05時是顯著的，而當(dāng)P值大于0.1時為不顯著。失擬性檢測的值為1.13，表明相對于純誤差不顯著，有43.75%的可能性在該項中出現(xiàn)這樣的數(shù)值。

根據(jù)回歸方程的F檢測和P檢測，選擇參與方程回歸的項，通過多次試驗可以得到基于實際因子水平的二階回歸方程：

η=1.165+0.762ε-2.85η+1.83φ+1.9εη+

0.178εφ-0.667ηφ-1.533ε2+1.738η2+0.022φ2

(6)

再通過diagnostics(回歸診斷)功能分析回歸模型擬合的優(yōu)劣。如圖3所示，殘差的正態(tài)概率分布點應(yīng)該盡量在一條直線上；如圖4所示，殘差與預(yù)測圖像點應(yīng)當(dāng)呈無規(guī)律分布。由此可見，建立的回歸方程是基本滿足診斷要求的。

圖3 殘差的正態(tài)概率分布圖

圖4 殘差與預(yù)測對比

通過Model Graphs功能可以產(chǎn)生二維、三維響應(yīng)面模型，如圖5和圖6所示。從圖5和圖6可以看出，三維響應(yīng)面模型呈現(xiàn)馬鞍形，說明優(yōu)化目標(biāo)在區(qū)間內(nèi)沒有明顯的極大值和較小值。不能采用通過響應(yīng)面等高線分布狀況判別極值的方向和位置，只能使用數(shù)學(xué)解析的方法。

圖5 二維響應(yīng)面圖像

圖6 三維響應(yīng)面圖像

2.3 優(yōu)化設(shè)計結(jié)果與驗證

選擇優(yōu)化目標(biāo)的性質(zhì)(極大、極小、逼近某一數(shù)值)和各個變量的取值范圍，在design-export中計算可得，靜壓效率的極大值為0.41，期望為0.112。當(dāng)靜壓效率達到極大值時，變量ε、η和φ分別取0.72、0.51和0.82。

根據(jù)式(3)由ε、η和φ的最優(yōu)取值反推出最優(yōu)的D、L和M值，可得493 mm、696 mm和433 mm。然后，用最優(yōu)的D、L和M值重新構(gòu)建空間模型，將這一模型按照原始條件重新進行仿真計算，優(yōu)化模型與原模型的仿真結(jié)果如表5所示。

表5 優(yōu)化模型與原模型的仿真結(jié)果

從表5可知，優(yōu)化模型在全壓效率上提高了13%，在靜壓效率上提高了9%，在噪聲方面的改變較小。這說明，本次優(yōu)化設(shè)計一定程度上是成功的。

3 結(jié)論

以某型號無蝸殼風(fēng)機箱為例，采用數(shù)值模擬與響應(yīng)面相結(jié)合的方法，對其箱體尺寸進行優(yōu)化，得出以下結(jié)論：

(1)在工程問題的優(yōu)化設(shè)計中，利用數(shù)值分析和響應(yīng)面模型相結(jié)合，可以減少研發(fā)周期并且降低成本。

(2)優(yōu)化結(jié)果表明，該模型使風(fēng)機全壓效率和靜壓效率都有所提升，對噪聲的優(yōu)化效果較小。