網格密度對計算流體力學仿真效率的影響研究

劉傳波，宋宗林

(武漢理工大學 機電工程學院，湖北 武漢 430070)

隨著汽車工業技術的發展，以及相關行業標準的提高，汽車外流場的數值模擬也日益重要。作為通用的分析方法，計算流體力學(computational fluid dynamics,CFD)在汽車外流場的在線仿真中起到了不可或缺的作用。而網格劃分，又是仿真模擬的關鍵步驟，網格劃分的質量好壞，直接影響著計算速度、精度以及收斂性。

近十幾年來，國內外相繼開展了這方面的研究。張少雄等[1]研究了網格劃分對于船舶方艙結構有限元分析計算的影響；鄭秋亞等[2]研究了網格密度對于飛行器機翼的方程計算的影響；鄧曦等[3]則研究了網格尺寸對于建筑結構有限元分析的影響；沈自尚等[4]研究了網格密度對于圓角圓弧結構的影響。國外的Deng等[5]研究了網格生成對船舶水動力學計算的影響；Lu等[6]研究了不同網格尺寸，對于船舶流場動力和力矩的誤差影響; Kisun等[7]研究了網格形狀對最終汽車仿真結果的影響;Lopes等[8]研究了網格密度對汽車外流場分布的影響。研究表明，網格劃分較細時，可以有效提高計算精度，但會延長計算時間；網格劃分較粗時，雖然會加快計算速度，但易使計算結果失真。進行有限元計算時，在保證計算精度的基礎上，應該合理劃分網格粗細，加快計算速度，提高效率。但是在CFD仿真，尤其是汽車外流場仿真分析中，相關的研究還比較少。

筆者以MIRA國際標準汽車模型為例，研究ANSYS網格劃分對于汽車外流場仿真分析的影響，探討網格劃分密度與計算精度、計算時間的量化關系，以尋求最優方案，完善CFD領域的相關研究工作，以期有助于今后相關研究的展開。

1 試驗方案設計

1.1 數學模型

采用MIRA國際標準快背式汽車模型，該汽車模型應用范圍廣泛，具有較強的現實意義。由于在生產實際中，人們習慣于把所使用的1：5油泥模型轉換為計算機仿真造型，并根據仿真結果確定最終方案[5]。因此，筆者也采用1：5的比例來構建汽車模型。

采用的計算域為：車前3倍車長，車后5倍車長，兩側各為2倍車寬，頂部為3倍車高。同時為提高計算精度，設置加密區域：車前1倍車長，車后2倍車長，兩側各為1倍車寬，頂部為1倍車高。另外，在輪胎與地面交界處，進行加密處理。

1.2 網格劃分試驗方案

以初始模型為研究對象，網格類型為統一生成三角形面網格，采用不同尺寸進行劃分。由于網格過密會嚴重影響計算時間，不應取得過密，因此分析中車身網格尺寸最密取為3 mm，最疏取為13 mm，設置10組不同尺寸進行分析。網格尺寸劃分如表1所示。對于輪胎與地面接觸處，進行加密處理，始終取為3 mm。

表1 網格尺寸劃分

1.3 其他條件的固定設置

研究中，只有網格密度是自變量，其他條件應保持不變。設置速度為30 m/s，即108 km/h。為提高計算精度，提高計算效率，采用高雷諾數的K-ε模型，用二階迎風差分格式離散控制方程；同時采用SIMPLE算法進行迭代計算[9]，迭代步數為2 000步。

設置的邊界條件如表2所示，實際位置如圖1所示。

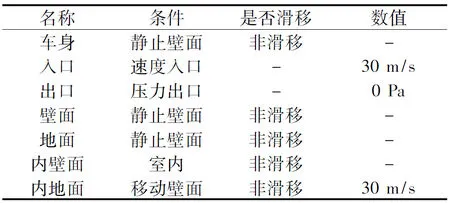
表2 仿真模型邊界條件

圖1 模型邊界條件實際位置

2 試驗結果及分析

2.1 試驗結果

試驗數據以初始模型為基準，以其風阻系數0.253 9為標準值，計算1～10號試驗風阻與初始模型的誤差。具體試驗數據如表3所示，包括每組試驗所用時間，風阻系數及其誤差。

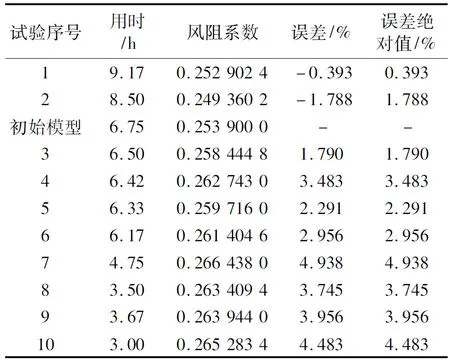
表3 試驗用時、風阻系數及誤差

2.2 網格密度與仿真精度相關性分析

分析表1車身網格尺寸與表3風阻系數誤差的關系，可以看出，隨著車身網格尺寸的加大，網格密度的降低，誤差也基本呈現增大的趨勢。

Spearman秩相關系數是分析兩個變量間相關程度的重要方法，應用廣泛。根據Spearman秩相關系數計算公式[10]，得出車身網格尺寸與計算誤差之間的秩相關系數為0.879,選取顯著性檢驗水平α=0.05，則Spearman秩相關系數檢驗臨界值cα(1)=0.564，因為0.879>cα(1)，可以認為網格密度與計算誤差成正相關，即網格密度越粗糙，計算誤差越大，計算精度越低。

通過SPSS數據統計分析，可以得到精度Y1與密度X之間的線性擬合回歸方程為：

ATB—25粗集料應選用堿性石料，不宜直接使用酸性石料；應使用錘式反擊破碎機加工碎石，以減少石料針片狀含量；所采用粗集料應干燥、潔凈、表面粗糙、形狀接近立方體，并且其規格與級配應較為穩定，本文選用的粗集料技術指標如表1所示。

Y1=-0.006 43+0.004 19×X

(1)

該方程通過統計檢驗，說明兩者之間存在顯著的線性關系。

2.3 網格密度與仿真速度相關性分析

依據表1的車身網格尺寸與表3的計算時間，可以看出，隨著尺寸增大，網格密度降低，計算用時也大幅度減少，計算速度越來越快。根據同樣的方法，可以計算出車身網格尺寸與計算用時之間的秩相關系數為-0.991，選取顯著性檢驗水平α=0.05，則檢驗臨界值cα(1)=0.536，-0.991<-0.536，車身網格尺寸與計算速度成高度負相關，即隨著尺寸增加，網格密度的降低，計算速度也隨之加快。

通過SPSS分析，得到速度Y2與密度X之間的擬合回歸方程為：

Y2=10.518-0.579×X

(2)

經過統計檢驗，說明兩者之間存在顯著的線性關系。

2.4 網格密度與仿真效果極值分析

為便于分析在不同網格密度下各計算結果壓力云圖間的關系，選用試驗1和試驗7作為研究對象，其中試驗1誤差最小，試驗7誤差最大，二者之間網格總數相差約530萬。

當汽車行駛在迎面氣流與汽車形成對流的過程中時，汽流首先與汽車車頭發生碰撞，氣流受阻，流速降低，從而產生一個正壓區。隨后，氣流產生分離，一部分向上經發動機引擎蓋、前擋風玻璃向車后流去；另一部分向下經過汽車底盤， 然后流向車尾。

流向汽車上部的氣流，在高速流過汽車前緣時，由于前緣處圓角曲率較小，氣流來不及轉折，因而產生氣流分離，流速較大，因而形成負壓區。隨后，氣流又回到汽車前端引擎蓋上，此時流速仍較大，仍為負壓區。由于前擋風玻璃阻擋了氣流的運動，而且在其底部存在凹角，因此氣流流速降低，形成正壓區。在汽車經過前擋風玻璃時，又形成一個轉角，形成一個負壓區。在汽車頂部比較平滑，氣流流速也較平緩，因而負壓值減少。流經車頂后，氣流沿后窗向下流動，在后窗與行李艙蓋的交界處發生氣流分離，形成正壓區。隨后，氣流又重新回到后行李艙蓋上，并在汽車尾部形成尾部負壓區。

另一部分向下的氣流，在汽車與地面之間的間隙流過，由于汽車底盤空間較狹窄，氣流流速快，因而形成負壓區。隨后兩股氣流匯合流向汽車尾部并相互作用，融合發展形成一個很大的尾部渦流，該尾渦區呈現負壓。

圖2 車身表面壓力云圖

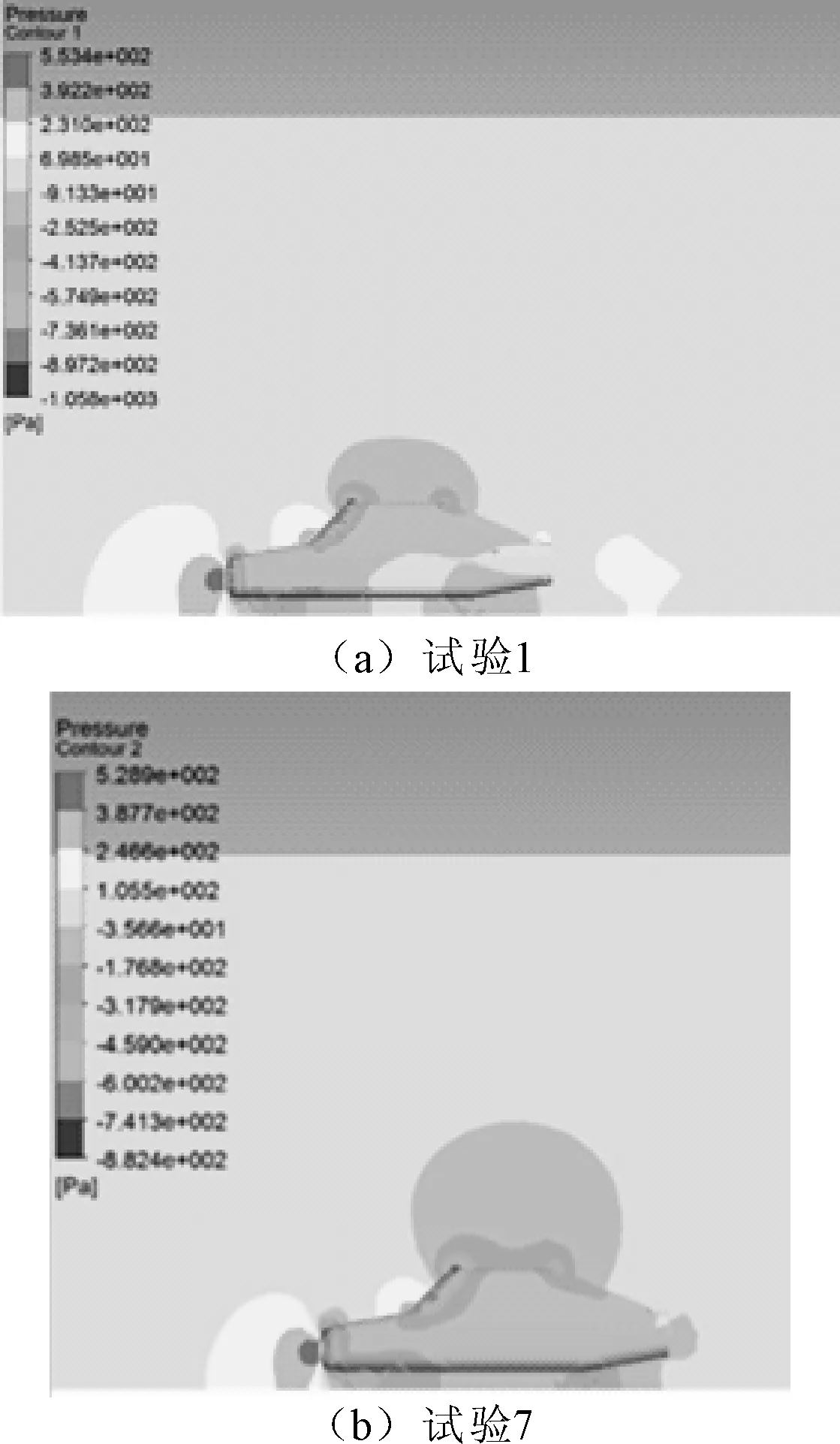
圖3 縱向對稱面壓力云圖

從圖2兩組試驗的車身表面壓力云圖及圖3兩組試驗的汽車縱向對稱面壓力云圖來看，在前擋風玻璃轉角處、車頂、后行李艙蓋這幾個主要的負壓區，密度較大的試驗1壓力云圖較為明顯。但在幾個主要的正壓區，兩組試驗則相差不大；并且，從云圖上的壓力數值來看，兩組試驗的壓力值基本接近。綜合上述分析，雖然密度粗糙的試驗7略有失真，但壓力云圖的分析基本在可允許范圍之內。

從圖4兩組試驗的縱向對稱面速度云圖來看，兩組試驗的汽車尾部渦流現象相差不大，只是試驗7的尾部倒流區相對有些紊亂。云圖數值上兩組試驗的氣流速度也基本接近。結合圖2分析，在正壓區汽流速度較慢；負壓區速度較快。相對于試驗1，雖然試驗7在車頂處氣流速度略小，但總體而言，兩組試驗的氣流吻合度相當。

圖4 縱向對稱面速度云圖

3 網格密度最優化分析

3.1 基于曲線交點的最優化

根據式(1)、式(2)，應用MATLAB作出雙Y坐標曲線圖，如圖5所示。從圖5可以看出，隨著車身網格尺寸的增加，計算誤差呈現單調遞減，而計算時間則單調遞增。在圖5中，誤差-尺寸曲線與時間-尺寸曲線，二者相交于橫坐標6～7之間，約為6.63。因此，選取橫坐標7作為最優化坐標點，即車身網格尺寸為7時，作為最優化設計方案。該方案可以實現仿真精度與計算時間的最優化組合。

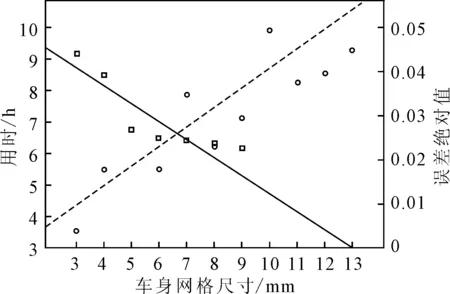
圖5 線性回歸擬合方程雙Y坐標曲線圖

3.2 基于時間最短的最優化分析

從表3可知，雖然計算誤差呈現一直增大的趨勢，但實際上風阻系數計算誤差始終較小，最小的低于1%,最大的也不到5%。也即在網格密度最粗糙的情況下，風阻系數計算誤差也在允許范圍之內。因此，在仿真分析中，可以將計算時間作為一個唯一考慮的影響因素。選取網格密度最粗糙的試驗10作為最優化方案，計算誤差為4.483%，但用時僅3小時，比初始模型縮短一倍以上的時間。這樣，既不會影響風阻系數的計算，同時也可以極大地節省計算機資源，縮短計算時間，提高仿真效率。

4 結論

通過對上述網格密度與計算速度、計算精度之間關系的分析，得出以下結論：

(1)通過Spearman秩相關系數分析，可以得出網格密度與計算精度呈現高度負相關，即網格密度越細膩，計算精度越高；網格密度越粗糙，計算誤差越大。該負相關關系也可以根據SPSS數據統計分析，得到線性回歸擬合方程，該方程經過統計檢驗，可以結合實際進行應用。

(2)通過Spearman秩相關系數，可以認為網格密度與計算速度呈現高度正相關，即計算時間隨著網格密度的增加而增加。應用SPSS可以得到二者之間的擬合方程，該方程可以結合實際進行應用。

(3)分析比較所得誤差最小的試驗1和所得誤差最大的試驗7這2兩組試驗結果，從圖2～圖4可以看到，雖然在前擋風玻璃和車頂處的壓力值，以及汽車尾部倒流區，試驗7略有失真；但考慮到仿真結果的隨機性誤差，就總體而言，可以認為二者的仿真結果基本相當。

(4)綜合上述分析，分別基于擬合曲線交點和時間最短，提出網格設計最優化的兩種方案。特別是在第二個方案中，將多目標優化約簡到單目標優化，最大程度地節省計算機資源，提高了仿真分析的效率。