求解第Ⅱ類裝配線平衡問題的混合遺傳算法

麻 娟，劉儼后，楚滿福，高 軍

(山東理工大學 機械工程學院, 山東 淄博 255049)

裝配線平衡(Assembly Line Balancing, ALB)是指在滿足特定的約束條件下，將裝配作業元素分配到不同的裝配工位上，使工位數和生產節拍合理，同時各操作工人的生產負荷盡量均衡[1]。1954年Bryton在其學位論文中正式提出ALB問題，并列舉了一些解決方法[2]；Salveson首次用數學解析的方法對ALB進行了研究，提出一個求解ALB問題的線性規劃模型[3]；Jachson在給定生產節拍條件下，采用枚舉法解決了最小化工位數量的ALB問題[4]。但是，ALB問題是一個NP-hard問題，在作業數量增加時，容易產生組合爆炸，數學解析法和一般的啟發式算法求解效果不理想。

近年來，遺傳算法(Genetic Algorithm, GA)在基礎理論和實際應用上均取得了長足的發展，在車間調度、制造元設計、車輛路徑、設備布局、網絡設計等許多組合優化問題中得到了成功應用。Noorul等將關鍵階位權重法引入GA的初始化過程，提出一種混合GA對ALB問題進行求解[5]；Kim等針對一個具體的問題設計特定的啟發策略與GA結合，加快算法收斂速度[6]；Mutlu等和Zaman等將工人操作技能作為約束條件建立了ALB問題模型，并設計了一種改進GA進行求解[7-8]；皮興忠等依據作業優先關系生成初始群體以及構造交叉算子和變異算子，保證搜索空間中個體的可行性，以提高算法的效率[9]；吳爾飛等針對雙邊裝配線的特點，提出一種基于序列組合編碼的GA，對ALB問題進行求解[10]；劉金山等設計了企業鏈和任務鏈的雙鏈GA，以解決制造資源優化配置問題[11]。

上述研究中，GA通過保留精英個體實現解空間信息的染色體遺傳共享，種群比較快速地向最優區域移動，收斂性較好。但同時也容易造成進化過程早熟，難以獲得最優解，而早熟收斂也是GA的一大缺陷[12]。為此本文提出一種混合遺傳算法(Hybrid Genetic Algorithm, HGA)，將煙花算法(Fireworks Algorithm, FWA)中基于免疫濃度思想的分布式信息共享機制引入GA，以保持進化過程中種群多樣性；將鄰域搜索引入變異操作，以改進算法的局部搜索性能。針對第Ⅱ類ALB問題的求解，將本文的HGA與其它典型算法進行對比分析。

1 平衡問題描述

為方便描述，文中涉及變量見表1。

表1 變量符號定義

Tab.1 Variable symbol

符號定義C生產節拍m工位數量n作業數量S工位集合,S={s1, s2, …, sm}sti工位si的作業時間A作業元素集合,A={a1, a2, …, an}ti作業元素ai的作業時間Bn×n作業優先約束0-1矩陣,bij=1表示作業aj必須在作業ai后面進行

一般可將ALB問題分為三類[13]：ALB-Ⅰ，固定生產節拍C，最小化工位數量m；ALB-Ⅱ，給出工位數量m，最小化C；ALB-Ⅲ，已知C和m，最小化均衡指數SI

(1)

在實際裝配生產中，設備和人員基本固定，隨著市場需求波動或工人操作經驗改變而導致作業時間發生變化時，企業更需要ALB-Ⅱ優化，以保證生產節奏適應市場變化，提高生產柔性。因此本文以ALB-Ⅱ為研究對象，在給定工位數量m下尋求最小節拍C，同時將均衡指數SI作為評價指標。基于表1所述相關變量，建立本文ALB-Ⅱ數學模型如下：

min(C，SI)

(2)

s. t.

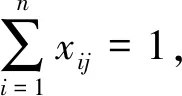
(3)

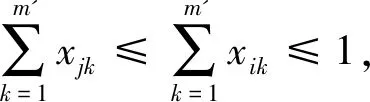
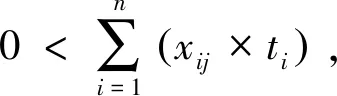
(5)

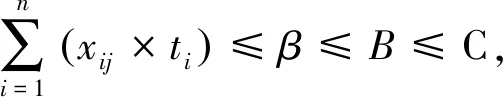
(6)

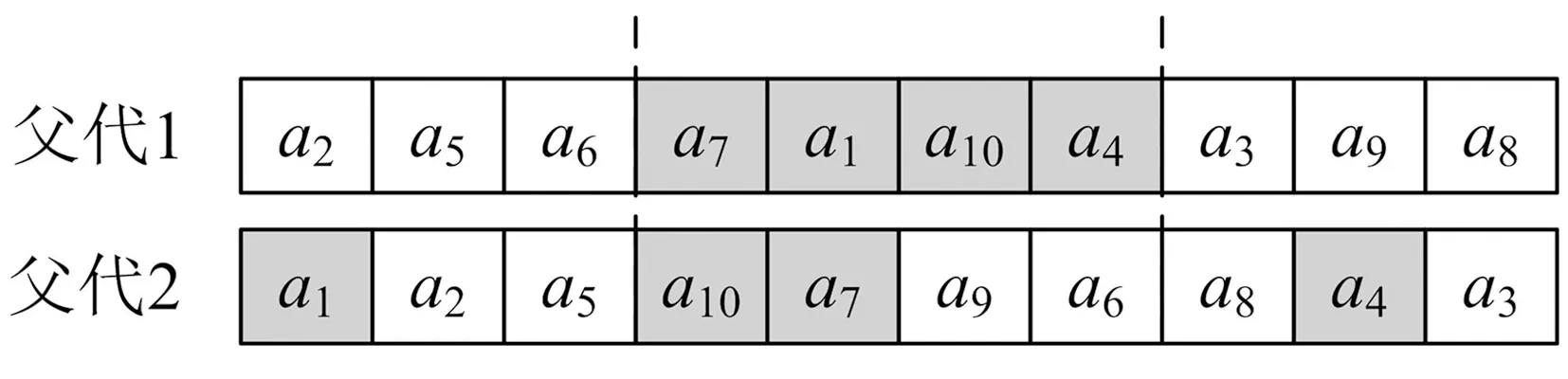
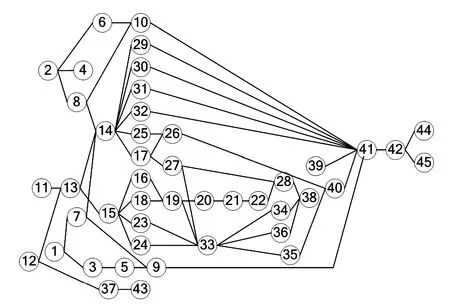
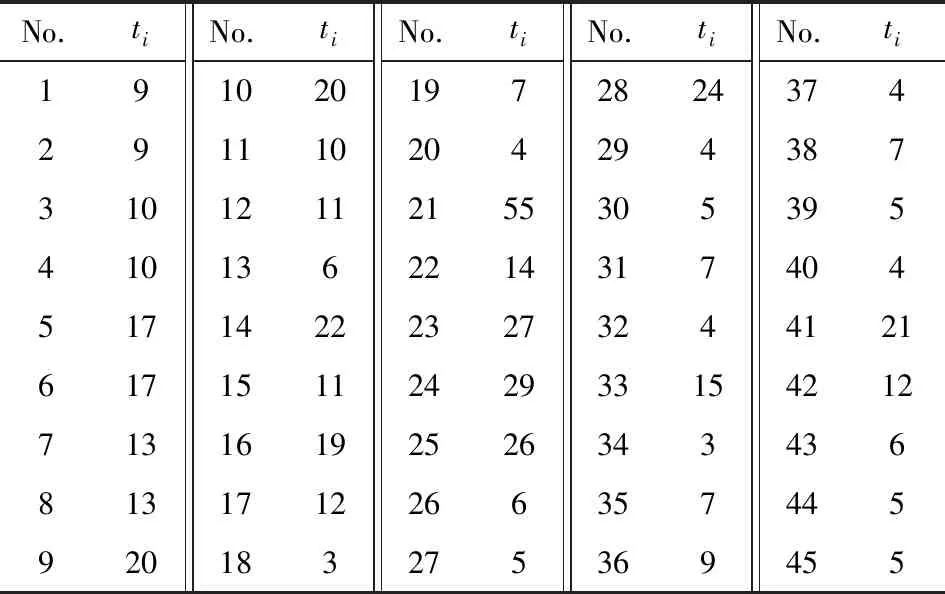
函數表達式min(x.y)表示優先最小化變量x，x值相等時最小化變量y，即若x1

決策變量xij=1表示作業ti分配到工位sj，xij=0表示作業ti未分配到工位sj。約束條件式(3)表示每個作業只能分配到一個工位，且每個作業必須被分配；式(4)表示約束優先關系被滿足；式(5)表示每個工位必須被使用；式(6)表示每個工位作業時間滿足節拍約束。

2 混合遺傳算法

在GA的進化進程中，適應度越高的父代個體參與繁衍后代的機會越多，而適應度低的父代個體逐漸被淘汰，這種精英保留策略使得種群較快收斂，但容易造成進化過程早熟，最終導致算法陷入局部次優，難以獲得最優解。FWA是一種新穎的群體智能算法，它通過爆炸、變異、選擇等進行爆炸式搜索，與GA具有相似的進化過程，但卻有本質上的不同。FWA采取免疫濃度思想(Immune Concentration, IC)的分布式信息共享機制，有利于保持種群多樣性，避免陷入局部最優解，但進化過程缺乏精英解的指導，容易陷入隨機搜索，造成計算資源耗費、難以收斂。為解決此問題，本文結合二者優勢，基于GA框架提出一種混合遺傳算法(HGA)：在選擇算子中引入IC思想，以保持種群多樣性；在變異算子中借鑒鄰域搜索(Neighborhood Search, NS)策略，以改進算法的局部搜索性能。

2.1 問題編碼

采用作業序列編碼方式，按作業分配至工位的順序進行編碼，每個作業元素對應于染色體上的一個基因位。如圖1所示，第一次分配a1，第二次分配作業a2，……，第九次分配作業a4，最后一次分配作業a3。

圖1 10個作業的染色體編碼Fig.1 Chromosome encoding of 10 tasks

ALB-Ⅱ問題的生產節拍C是未知的，在解碼的時候不能按照C去分配作業，對于這個問題的解決思路是預估一個C*，以C*為約束按照一定的增量進行探索求解計算。由于ti的離散性，C*的增量是不連續的，而是以ti作為增量。解碼過程如下：

(1)計算理論最小節拍Ct=(Σtk)/m，其中Σtk表示所有作業元素作業時間之和，m為給定的工位數量，令C*=Ct。

(2)以C*為節拍，按照染色體編碼作業序列把n個作業分配到m個工位中，如果每個工位作業時間均滿足sti≤C*，則C*就是在這種排序下的最小節拍，搜索停止；否則轉(3)。

(3)計算工位sti的潛在增量d1，d2，…，dm，其中di(i=1, 2, …，m-1)表示工位si+1的第一個作業元素作業時間，dm=0。

(4)令C=max{sti}，C*=min{sti+di}，若C≤C*，則C就是此染色體編碼排序下的最小節拍，搜索停止；否則轉(2)。

HGA的初始化是隨機生成N個個體編碼的過程，種群Q={q1,q2, …,qN}，然后通過交叉算子、變異算子和選擇算子，基于初始種群完成進化搜索。

2.2 基本操作算子

2.2.1 交叉算子

交叉算子采用兩點交叉法，如圖2所示，隨機產生兩個交叉點，在父代2中搜索父代1基因段的排列方式，進行交叉替換獲得子代1，同樣的交叉過程獲得子代2，如圖3所示。這種交叉操作能夠保證子代個體為可行解，減少計算量，提高算法效率。

圖2 兩點交叉算子Fig.2 Two-point cross operator

圖3 子代的編碼Fig.3 Encoding of offspring

2.2.2 變異算子

個體的染色體進行獨立的變異，采用單點變異，隨機產生一個變異點，對變異點后面的基因段進行重新排列。重新排列的過程，即根據優先關系矩陣重新分配作業的過程，獲得新的子代，如圖4所示。

圖4 染色體變異操作Fig.4 Mutation operator of chromosome

2.2.3 選擇算子

適應度評價函數是區分種群個體優劣的標準，是進化中優勝劣汰的唯一依據。ALB-Ⅱ的優化目標是生產節拍C最小化，本文將SI作為第二評價指標，如式(2)所示。

f1=min(C);C=max(sti)

(7)

(8)

(9)

函數len(x)表示獲取數值x的整數位數，即式(9)表示將f1作為整數部分，f2作為小數部分，組合得到數值f，f越小則適應度越優，符合式(2)要求。

根據適應度評價，從子代種群中選取下一代種群，除最優個體外，其余個體采用輪盤賭規則選出，選擇概率為

(10)

2.3 基于NS的交叉操作

在基本變異算子中引入鄰域結構，提高HGA的局部搜索能力。在變異操作中獲得子代以后，隨機產生兩個變異點，在兩點范圍內生成鄰域結構(在矩陣B約束下重排序)，如圖5所示。

圖5 變異中的鄰域結構Fig.5 Neighborhood structure in mutation

對鄰域空間進行局部搜索會占用大量的計算資源，進而影響算法效率，HGA會根據算法迭代次數控制鄰域規模進行變鄰域搜索，變鄰域規則如下：

(11)

式(11)表示變異操作時需進行鄰域搜索的概率，其中t為迭代次數，T為最大迭代次數。通過變鄰域可以實現種群在進化初期進行較大范圍的鄰域搜索，而到了進化后期，只需要進行小范圍鄰域搜索來達到尋優的目的，既提高了算法局部搜索性能，也能保證搜索效率。

2.4 基于IC的選擇操作

基本選擇算子通過精英策略選擇子代，算法收斂性較好，但容易早熟收斂。將FWA爆炸算子中的IC策略引入選擇算子，以提高種群多樣性。定義選擇概率pI為

(12)

(13)

式中，‖qi-qk‖表示個體之間的歐式距離，即個體與其它個體偏離越大，其被選中的概率越大，從而避免了多樣性損失，但也容易使算法陷入隨機搜索過程。結合GA的精英保留策略和FWA的IC選擇策略，定義HGA的選擇算子概率為

p(qi)=λ1pE(qi)+λ2pI(qi)

(14)

式中0≤ λ1≤ 1，0≤ λ2≤ 1，λ1+λ2= 1，通過系數可調整精英保留策略和IC選擇策略的權重。HGA綜合了GA收斂性好和FWA種群多樣性優的特點，提高了算法全局搜索性能。

2.5 HGA基本流程

HGA的基本流程如圖6所示，其中算法終止條件為最大迭代次數。

圖6 HGA的基本流程Fig.6 Flow chart of HGA

3 算例求解

Kilbridge問題是一個10工位ALB測試問題[14]，工位數m=10，作業數量n=45。Kilbridge問題作業優先約束關系如圖7所示，作業時間見表2。

圖7 Kilbridge問題作業優先關系Fig.7 Precedence relation of Kilbridge-problem

將HGA、GA以及文獻[15]基于成組工序遺傳算法(Group Technology Genetic Algorithm, GGA)進行求解結果對比，種群規模N=300，交叉概率取0.6，變異概率取0.4，迭代終止條件為最大迭代次數200；進行100次重復試驗，算法各自尋到的最佳解作為算法的最優解，求解結果見表3。

表2 Kilbridge問題作業時間

Tab.2 Task’s time of Kilbridge-problem min

No.tiNo.tiNo.tiNo.tiNo.ti19102019728243742911102042943873101211215530539541013622143174045171422232732441216171511242933154212713161925263434368131712266357445920183275369455

表3 Kilbridge問題求解結果

Tab.3 Solution of Kilbridge-problem

求解算法最優解CSI最優解次數平均運行時間/sGA588.7233/10036.5HGA564.0078/10027.1GGA564.1272/10039.0

從表3可以看出，在最優解求解能力方面，HGA和GGA相當，且均優于GA；在算法求解效率方面，HGA優于GGA和GA。

4 結束語

裝配線平衡是典型的組合優化問題，作業優先約束增加了問題復雜性，針對第Ⅱ類裝配線平衡問題，提出一種混合遺傳算法進行求解。HGA將FWA爆炸算子中基于免疫濃度思想及GA中精英保留策略進行結合，設計了選擇算子，以保持進化過程中種群多樣性；同時將鄰域搜索策略引入變異操作，以改進算法的局部搜索性能。通過第Ⅱ類裝配線平衡問題實例，將本文的HGA與典型GA進行對比分析，驗證了HGA的有效性，為裝配線平衡問題的解決提供了一種新的方法。