風力發電機塔架風致疲勞壽命評估

陸 越，于安林，陳 鑫

（蘇州科技大學 江蘇省結構工程重點實驗室；江蘇 蘇州 215011）

近年來，隨著傳統能源的逐漸枯竭和環境問題的日益突出，風能作為一種清潔無污染的可再生能源，受到世界各國越來越多的重視。目前風力發電已經成為風能資源利用的主要方式，風力發電機結構研究也就應運而生。風力發電機組的特點有質量輕、阻尼小、固有頻率低等，是典型的風敏感結構，而風荷載導致的結構疲勞破壞是風力發電機結構設計中首要問題。

JUAN[1]建立了風機驗證模型，準確地解釋了齒輪箱動態及激發系統的外部動力學，并對風機進行了疲勞分析。疲勞分析表明，在軸承損壞的等效負載的影響下水平損壞程度更高。Yeter[2]對各種負載條件下的海上風力渦輪機的支撐結構的時域疲勞損傷進行評估，從不同區域的支持結構的許多熱點進行了分析。在頻域中結合聯合波和風光譜，將所得的應力譜密度函數的定義成逆快速傅立葉變換方法的應力時程，最后提出支撐構件不僅是結構的一個重要組成部分，在承載能力方面也受到最嚴重的疲勞損傷。裴舟滔[3]研究了反向平衡法蘭熱點有限元分析，根據反向平衡法蘭的受力特性，提出應選取法蘭板與筒壁間焊縫的筒壁側焊趾為疲勞評估的關鍵位置。尹艷杰[4]根據內蒙古武川風場的場地條件，基于有限元軟件分析塔架在隨機風荷載下的風振響應，對風電塔架承受的隨機風荷載進行數值模擬。基于線性累積損傷理論和S-N曲線來獲取塔架在設計使用壽命內的疲勞累積損傷，估計出塔架的疲勞壽命，從而評估結構的安全性。

本文基于某5 MW大型風力發電機結構，建立了多尺度有限元模型，并根據模擬的風荷載對風力發電機塔架進行動力分析，再結合miner線性累積法則[5]和雨流計數法[6]對結構的關鍵部位進行疲勞壽命的評估。

1 有限元模型的建立

基于5 MW三風輪風力發電機系統[7]，風力發電機塔架是細長的薄壁鋼管結構，為簡化模型，忽略各段之間法蘭盤的連接部分，認為塔體為統一整體。塔高90 m，底徑6 m，頂徑3.87 m，塔體通長為變截面結構，底壁厚35.1 mm，頂壁厚24.7 mm，通長厚度由底部至頂部呈線性減小趨勢。各槳葉間呈120°夾角，沿軸向平均分布，風輪直徑123 m，采用矩形變截面，初始段長3 m，寬0.8 m，厚度為10 mm，風輪和塔體材料為Q345鋼。機艙質量為24 000 kg，輪轂質量為56 780 kg，每一個葉片的總質量為17 740 kg，共3個。

采用大型商業軟件ANSYS進行模型建立，建立了梁單元與實體模型相結合的多尺度有限元模型（見圖1），上部塔架與葉片采用beam188單元，根據圣維南原理，確定了與土相連的塔體根部實體模型的高度，塔架根部采用solid186實體單元。在ANSYS有限元模型中葉片與機艙連接處設了一個Combine14單元，其X方向的扭轉常數為867 637 kN·m/rad，阻尼為6 215 kN·m/rad。在上部塔架和塔架根部實體模型建立時，由于兩者選用的單元的自由度不一樣，所以要引用約束方程的概念。文中采用MPC法，MPC法就是在實體單元的接觸面形成剛性梁域（剛性面），最后將梁直接與中心節點相連，如圖2所示。圖2（a）為桿單元與實體單元連接的局部多尺度有限元模型，圖2（b）為開啟梁單元截面顯示后的多尺度模型。

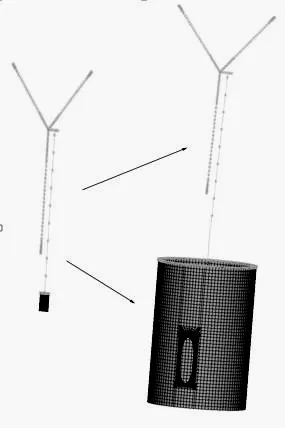
圖1 多尺度有限元模型

圖2 局部多尺度模型詳解

應用ANSYS和SAP2000有限元軟件對上述風力發電機桿系模型進行有限元模態分析，其中ANSYS提取模態振型時采用Block Lanzos模態提取法。Block Lanzos法功能比較完善，能夠提取大型模型中的多階振型，且此方法在計算精度和效率上都有較大的優勢。ANSYS桿系模型、SAP2000桿系模型與ANSYS的多尺度有限模型的前八階自振頻率如表1所列。

2 塔架脈動風的模擬

風力機的脈動風模擬分為塔架脈動風和葉片脈動風的模擬，由于本文主要研究的是塔架的疲勞評估，所以將葉片所承受的風荷載直接加到了塔架的頂點上，這里主要介紹塔架的脈動風的模擬。

2.1 模擬方法

采用諧波疊加法來模擬塔架來流風速的時程，該方法是由Shinozuka提出的平穩隨機過程進行離散化數值模擬的一種研究方法。相干函數是空間風場結構重要的表達方式，在進行脈動風模擬時，必須考慮結構所受脈動風的空間相關性，本文選用的Davenport譜的相干函數，其表達式如下

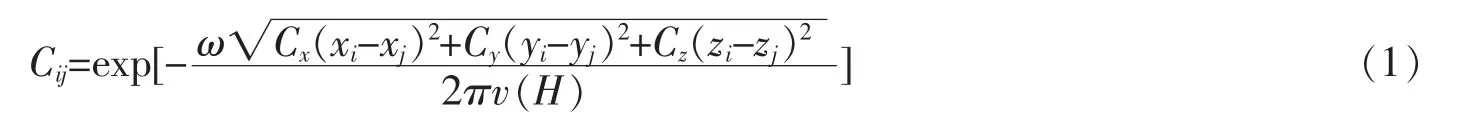
式中，Cx、Cy、Cz為葉片和塔架上任意兩點橫向、順風向、垂直向的衰減系數，Cx=16，Cy=8，Cz=10。v（H）為高度 H處平均風速。

在脈動風速的數值模擬工程中應用我國荷載規范采用的Davenport譜[8]，公式如下

式中，n為順風向脈動風頻率；S（n）為Davenport水平脈動風譜；v*為流動剪切風速，，k與地貌有關（本文取 0.03），為 z=10 m 高度的平均風速；。

定義風機上n個風速模擬節點，假定均為零均值的平穩高斯過程，其風譜密度函數矩陣

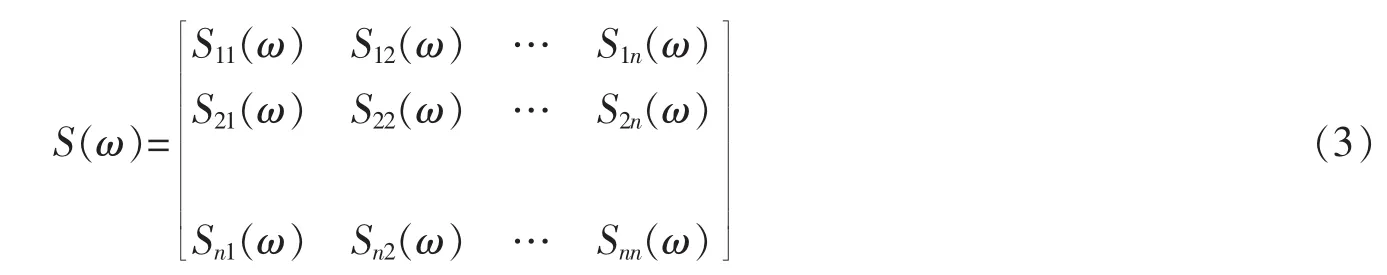
式中，Sii（ω）為節點脈動風自功率譜，采用式（2）中的風譜模型計算；Sij（ω）為互功率譜，加權公式如下

再將進行Cholesky分解，此時風力發電塔架上的任何一個節點脈動風速時程可由其功率譜決定，根據Shinozuka理論，模擬的風速時程可表達為

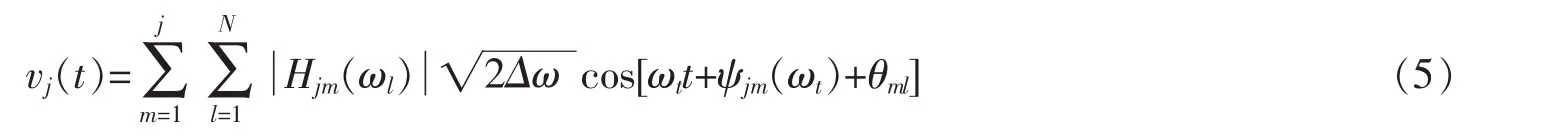
2.2 模擬結果

利用上述的諧波疊加法，通過matlab編程對風荷載進行數值模擬。在整個風力發電機中選取了塔架上的四個脈動風速計算點，分別為A、B、C、D，計算模型如圖3所示，在計算過程中脈動風的上限頻率取4π，脈動風頻率分割點數為2 048，頻率增量Δω=0.006 14 Hz，當地50 y一遇的基本風壓為0.35 kN/m2，故取當地10 m高的平均風速為24 m/s。A、D兩點的瞬時風速時程分別如圖4與圖5所示，其相應的功率譜和相干函數如圖6與圖7所示。可以看出，模擬所得風速功率譜與目標譜較吻合，趨勢基本一致，所模擬的相干函數效果相對較好，由此可知本節所采用的方法能較準確地實現風荷載的模擬。

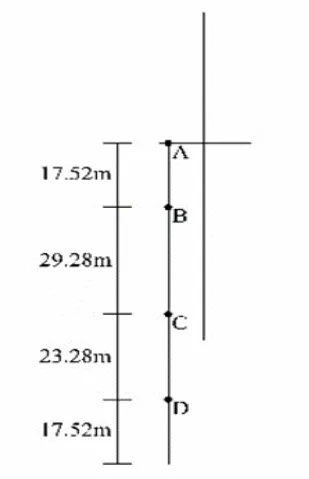
圖3 風力發電機風力計算點模型

圖4 D點風速時程

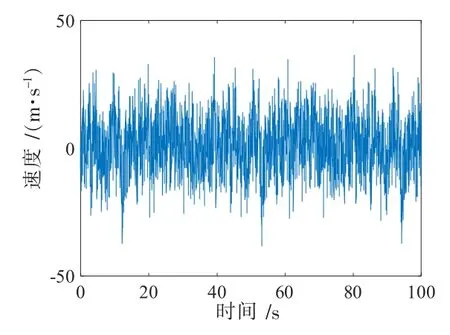
圖5 A點風速時程

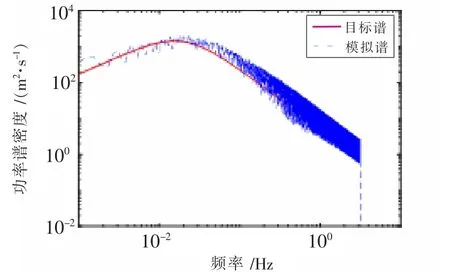
圖6 D點風速功率譜密度

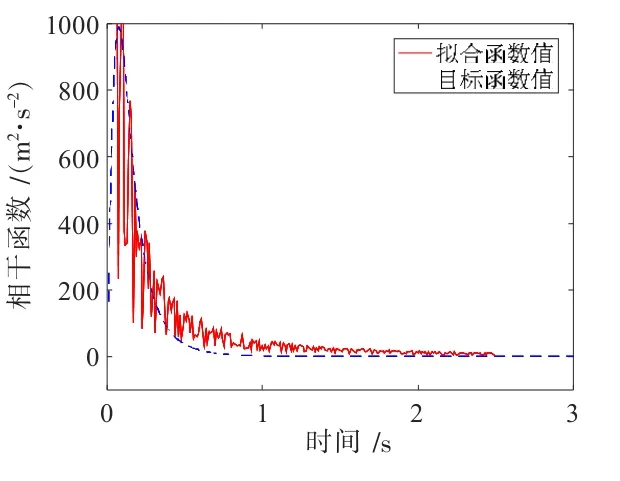
圖7 A、D點風速相干函數

3 疲勞損傷分析

對于風力發電機塔架而言，易產生疲勞的地方主要在底部連接處和門洞的開孔位置，選取的是底部連接處的關鍵點，運用名義應力法，結合雨流計數法和miner線性損傷法則來預估風力發電機塔架的疲勞壽命。

3.1 S-N曲線

通常為了評價和估算疲勞強度和壽命，需要建立外荷載與疲勞壽命之間的關系，外荷載通過應力S的形式表現出來，所以稱它們之間的關系為S-N曲線。材料的S-N曲線表現的是在應力的循環作用下材料發生疲勞斷裂的疲勞壽命，表達式如下

式中，α和C是疲勞試驗的參數，與材料、應力比、加載方式等均有關系，可以通過試驗得到；一般用σ代替S，β代替α。對上式同取對數，得

式中，A=lgC、B=-β。

上式是通過常幅循環應力試驗建立起來的，適合等幅應力下的高周疲勞。考慮平均應力的影響，一般需要通過Goodman公式進行修正，如式（8）所示，通過式（8）的轉化即可得到平均應力不為零時材料的疲勞失效模型。

式中，σa為實際外加應力幅；σ0為零平均應力的等效應力幅；σm為平均應力；σb為材料極限強度。根據鋼結構設計規范[9]，取名義應力法的S-N曲線的對數表達式

3.2 線性累積損傷理論

由于本結構屬于線性結構，本文采用Miner理論進行線性損傷疊加，Miner線性疲勞累積損傷的計算主要有以下幾點：（1）計算荷載單獨作用時對結構產生的損傷。假設周期為20 y，在已知隨機幅值的情況下求出對應的應力均值，再根據應力均值求出相應的循環次數；然后根據修正求出修正后的隨機應力，并確定修正后的隨機應力下的疲勞的循環次數，最后該荷載對結構產生的損傷就為應力均值下的循環次數與修正后的隨機應力下的循環次數的比值。

（2）計算損傷累積量

式中，ni為應力均值的循環次數，Ni為修正后的隨機應力的循環次數。

（3）計算疲勞壽命

3.3 壽命預測

基于5 MW風力發電機，結合所模擬的風荷載進行動力分析，通過雨流計數法、Goodman應力修正、S-N曲線和Pelmgren-miner線性累積損傷理論方法，再考慮風向概率的影響，最后得到20 y的損傷量（見表2）。

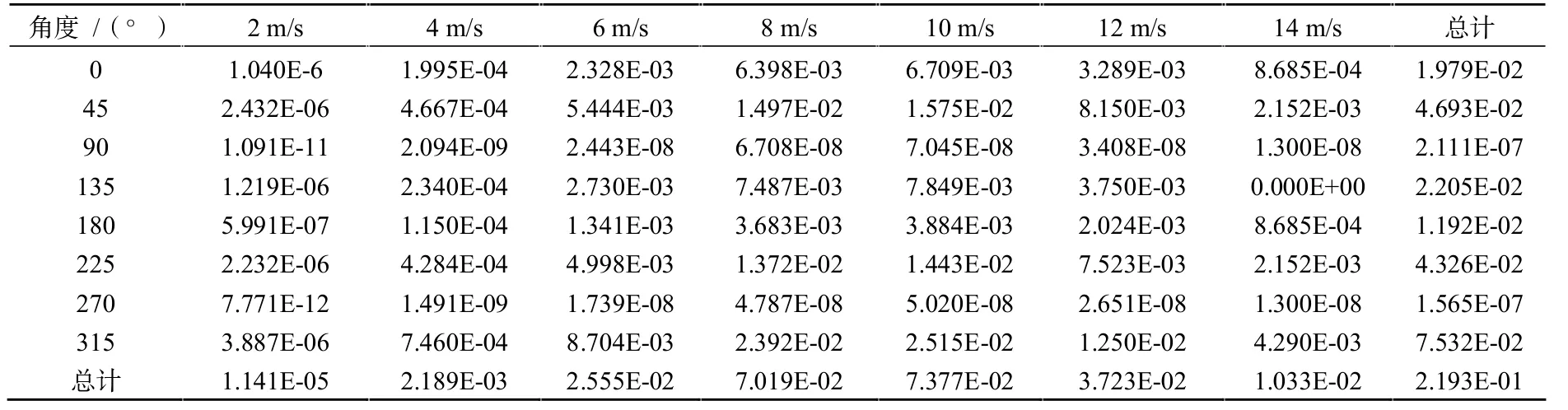
表2 風力發電機塔架底部關鍵點損傷量

結果表明，塔架底部連接處考慮風荷載，在名義應立法下預估的疲勞壽命為91.3 y，遠遠大于塔架的設計使用年限20 y，所以根據名義應力法預估的塔架的疲勞壽命是滿足設計使用年限的。

4 結論

（1）風力發電機的模態分析結果表明，ANSYS與SAP2000所模擬出的前八階頻率基本相同，誤差最大在第三階陣型，為4.29%，與實測數據幾近相同，其各階振型變形模式也完全相同。（2）塔架底部連接處考慮風荷載，在名義應力法下結合雨流計數法、Goodman應力修正、S-N曲線和Pelmgren-miner線性累積損傷理論，再考慮風向概率的影響得到最后的20年的損傷量為0.219。（3）基于名義應力法預估的塔架的疲勞壽命為91.3年，滿足設計使用年限。