基于敏感性的冗余度在框架結構優化設計中的應用

沈利來 ， 繆衛清 ，常 軍

（1.蘇州科技大學 土木工程學院，江蘇 蘇州 215011；2.蘇交科集團股份有限公司 江蘇 南京 210019）

縱觀國內外土木結構，六面體形狀因其剛性的合理性最大已被廣泛應用于土木工程領域。作為六面體代表的框架結構具有“部件數量多，冗余度高”的特點[1]。即使部分構件由于外界災害而降低承載力，但由于應力重新分配到其他構件而對整個結構的承載能力影響不大[2]。為了定量地顯示這樣的屬性，冗余度應運而生。采用冗余度評估結構的安全性和穩定性，并根據評估結果優化結構設計，使設計結構更加經濟安全合理是該領域的一個研究熱點。

丁銳等[3]從單元的勢能方程出發得出了剛性結構構件冗余度的計算方法，分析了冗余度與結構外荷載、幾何構造、截面參數以及約束情況之間的關系；郭冬梅等[4]研究了不同冗余度RC框架結構的抗震性能，降低結構冗余度，即減小結構某一方向跨數，或增加結構某一方向跨度，結構最大層間位移角增加，延性系數和屈服強度系數減小，結構彈塑性變形能力和承載力儲備能力降低，抗震性能變差。朱南海等[5]則選擇利用彈性模量的敏感性為參數基于材料的應變響應計算了單層球面網殼結構的冗余度，通過試驗模擬對比得出結論，冗余度可以衡量構件在結構中的重要性，冗余度較小的構件為關鍵構件，其損傷對結構整體影響較大。袁行飛等[6]人通過梁系結構的變形勢能方程探討了構件參數和約束條件對單元冗余度的影響，桿件的單元冗余度隨剛度的增大而減小，約束條件剛接變鉸接時結構整體冗余度變小。

上述研究在某一方面都取得了一定的成就，但對結構冗余度都沒有統一的定義，且大都以承載力為指標，較局限。微觀層面構件單元的冗余度和宏觀層面的結構的冗余度往往不加區分統一計算。論文采用考慮材料屈曲時的冗余度指標GNR[5]，設置了剛性框架結構的模型，使用敏感性指標來分析模型，并且研究GNR分布以獲得框架結構的冗余特性。另外，考慮到通過分析獲得的GNR分布來執行構件的優化布置。本文的目標是通過仔細研究結構特征來創建充分利用結構冗余特性的較優設計的結構。

1 冗余評估方法

1.1 概要

結構的冗余度與結構元件的非敏感性成正比，也可以說與其結構單元的敏感性成反比。定義見式（1）。

其中，Vi為i元素的體積。

根據式（1），Barai等定義了一種廣義的構件單元j冗余度指標[7]：

其中，n為元素的數量，V為結構的總體積，Sij為j元素損壞時i元素的敏感性。

通過標準化（歸一化）上式可得到如下定義：

1.2 敏感性分析

考慮材料屈曲，,通過引入許用應力的概念并且取應力與許用應力之比[8]對截面積A的敏感性，式（2）中的響應敏感性[9-10]定義如下：

針對框架模型，構件單元有壓縮拉伸兩種情況，并且考慮彎曲情況，定義如下：

其中，σc為壓縮應力；cσb為壓縮側彎曲應力；fc為容許壓縮應力；fb為容許彎曲應力；σt為拉伸應力；tσb為拉伸側彎曲應力；ft為容許拉伸應力。

1.3 余量平均值

余量可視作在一個線性范圍內，其定義為從1減去已經使用的和損傷耗損的結構性能占比之和[11]。而結構性能采用應力參數指標，具體定義如下：

其中，fi為i元素許用應力；σ為構件中產生的應力；A為橫截面面積；ΔA為損傷的橫截面面積。

在這種情況下，為了獲得部分構件損壞時對整體的影響，計算RRi時使用運算平均值RRave。

2 框架模型的冗余特性

2.1 分析模型

如圖1－圖3所示為3層的3乘3框架模型，固定支撐，剛性連接。加載條件是3.8 kN的垂直載荷和1.14 kN的水平載荷的節點載荷，具體作用位置見圖3中粗線層次中的每一個節點上，即每一層的梁和柱相交的節點處，共計48個節點處作用荷載。截面為0.125 m×0.125 m的矩形鋼截面，每段梁柱均為2 m，柱的彈性模量2.1×1011Pa，梁的彈性模量2.1×1015Pa。泊松比0.3，屈服應力3.45×108Pa。每一層的梁標號詳見圖2，每一層的柱標號與梁標號類似，見圖3。具體型號規格見表1。

2.2 分析結果

2.2.1 GNR分布

首先通過有限元軟件建立模型，加載分析得出每個構件的應力，包括彎曲應力和拉伸應力或壓縮應力，再將結果通過Matlab程序編程導入計算出最終的GNR值。采用Matlab編程可以使計算方便快捷，最后得到框架模型的所有柱和梁的GNR分布，詳見圖4和圖5。

圖1 框架模型

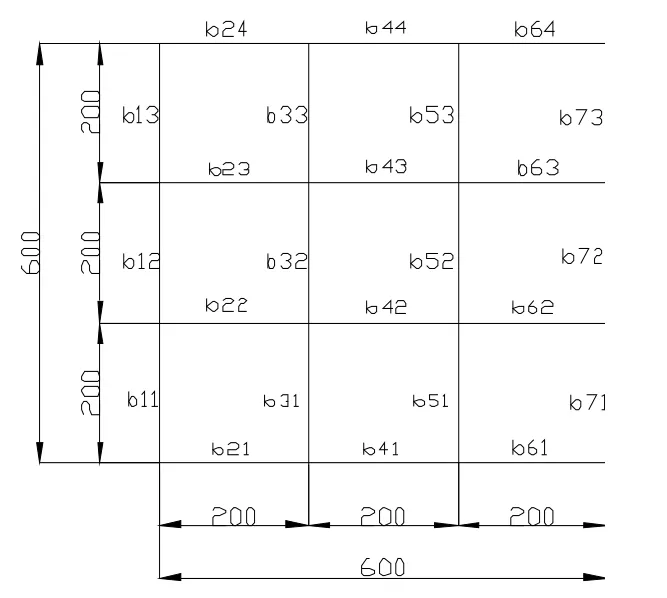
圖2 框架俯視圖（cm）

圖3 框架正視圖（cm）

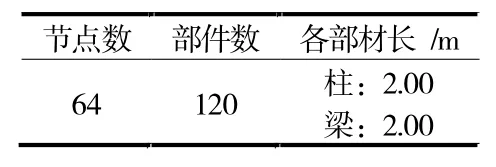
表1 型號規格

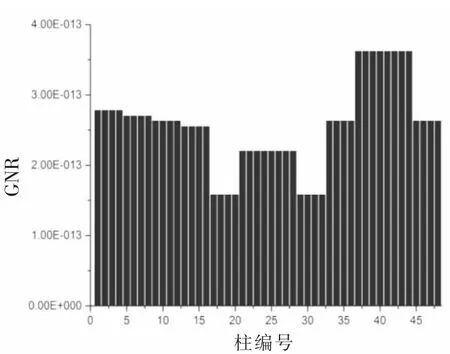
圖4 柱GNR分布

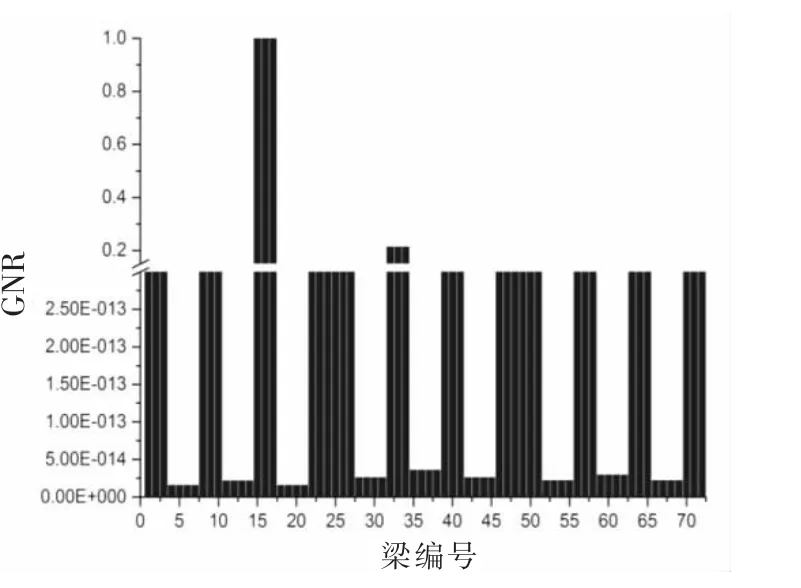
圖5 梁GNR分布

該框架模型一共48根柱，72根梁，為了使GNR分布顯示更方便清晰，其中柱編號1—16為第一層的柱，17－32 為第二層柱，33－48 為第三層柱。與此類似，梁編號 1－24，25－48，49－72 分別為第一、二、三層的梁。由圖4可以看出，柱的GNR分布數值較小，在數量級10-13左右，這與施加荷載大小、形式有關，且每層柱之間的GNR值也有差距，同一層柱之間也有高有低，例如第二、三層。表明現有柱的冗余特性分布不均。梁的GNR詳見圖5，由于不同梁的GNR分布數量級相差較大，這是GNR定義導致的，不可避免的，為了完整的比較所有梁的GNR值，縱坐標刻度采取了不等分和斷開措施。可以看出梁的GNR分布的數值也有高有低，但是有其規律，因為在受水平荷載時，由于框架模型中存在兩個方向的梁，所以即使承受大的水平荷載的梁受到損傷，應力在另一個方向的梁上流動，所以梁會出現這種GNR分布，根據柱和梁的GNR分布圖，可以認為現有結構梁和柱的冗余特性分布都不均。

2.2.2 余量均值研究

考慮部件冗余特性的余量平均值，把重點放在冗余度低（GNRmin）的部件和許用應力比大（應力值大）的部件上，當然作為對比，冗余度高（GNRmax）的部件也將一起進行計算研究。圖6便是3乘3框架結構冗余特性的余量均值圖，橫坐標為部件損傷率，是部件損傷面積比上完好狀態下時的面積。

根據上面的梁和柱的GNR分布圖，選取GNRmin和GNRmax相對應的部件為第一層的梁B21和B51。許用應力比最大的部件為第一層的柱C41。

在該框架模型中，當選定部件的損傷率達到0.5左右時，GNRmin和許用應力比最大的兩個部件的冗余特性余量均值略有所下降，當損傷率達到1時，即完全損傷時，下降幅度也較小。而GNRmax的部件的冗余余量均值則不變化。由圖6可以得出結論，該框架結構由于具有較多的梁和柱部件，所以即使個別部件損壞，對整體的影響也較小。

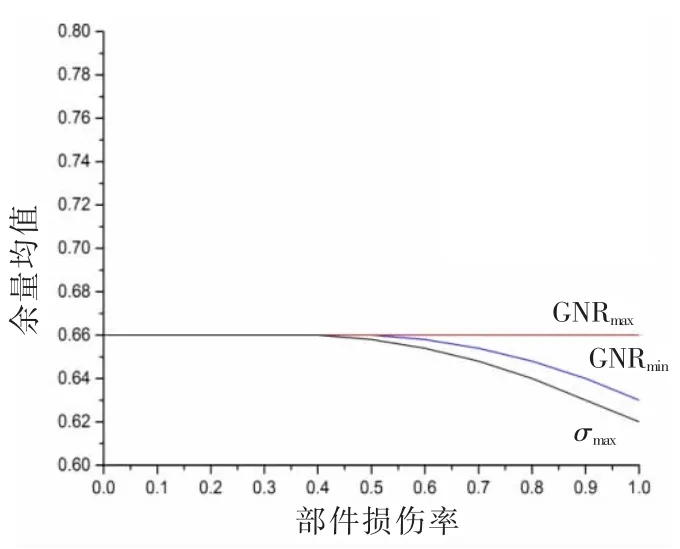
圖6 余量均值圖

3 優化框架冗余度

3.1 概要

根據圖4和圖5所示的柱和梁的冗余GNR分布，將一部分具有較低冗余度的構件改為具有大橫截面積的構件，考慮材料的非線性。為了進行優化后的前后對比，在這設定一個總質量不變的標準。隨即增大低冗余度部件橫截面積的同時，也要減小高冗余度部件的橫截面積。作為使用的材料，使用以下規格所示的方鋼管。部件布置圖詳見圖7和圖8。其中點畫線部件為增大后的部件，虛線為減小后的部件，實線是沒有變更的部件。 （變更前：125 mm×125 mm；變更后（增大）：150 mm×150 mm；變更后（減小）：100 mm×100 mm）

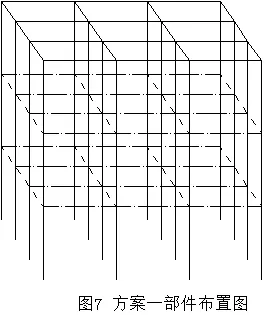
圖7 方案一部件布置圖

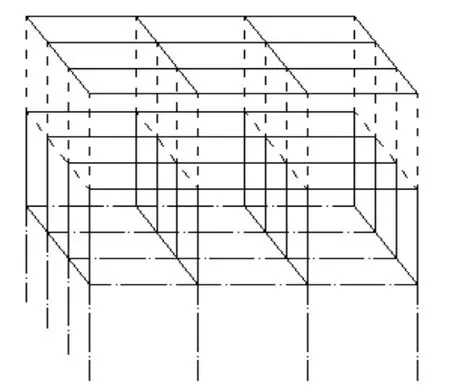
圖8 方案二部件布置圖

為了比較優化前后結構的冗余度，應注意初始屈服后屈服應力的延伸。因此，使用冗余延伸率Rcy來表示[12]。

其中，Pcol為結構體系的極限荷載；Pyiel為初始屈服荷載。

表達式（8）中的冗余延伸率表示從初始破壞到塌陷破壞的負載延伸相對于塌陷破壞負載的比率。其值范圍在0到1之間。該值越大表明該結構被評估為冗余度高的結構[13-14]。

3.2 分析結果

3.2.1 GNR分布

通過運用冗余評估方法，優化方案一的柱和梁的GNR分布見圖9和圖10。方案二的柱和梁的GNR分布見圖11和圖12。

根據以上兩個優化方案的柱和梁的GNR分布，對比變更之前的GNR分布可以看出，方案一的柱的GNR值整體較變更之前有提高，但分層現象較明顯，每層柱的GNR值差距不大。方案二的柱的GNR分布較均勻，無論是層與層之間還是同一層柱與柱之間。優化后的兩個方案的梁的GNR值較變更前都有明顯的提高，且橫梁縱梁之間的GNR差距有減小，表明優化后出現了更多的高冗余梁部件。

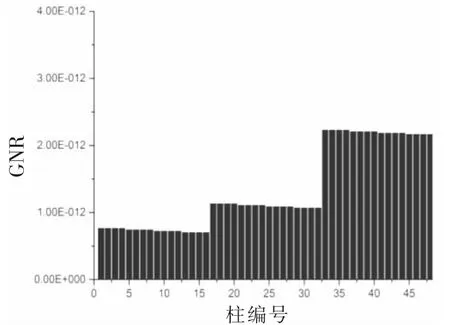
圖9 柱的GNR分布

圖10 梁的GNR分布

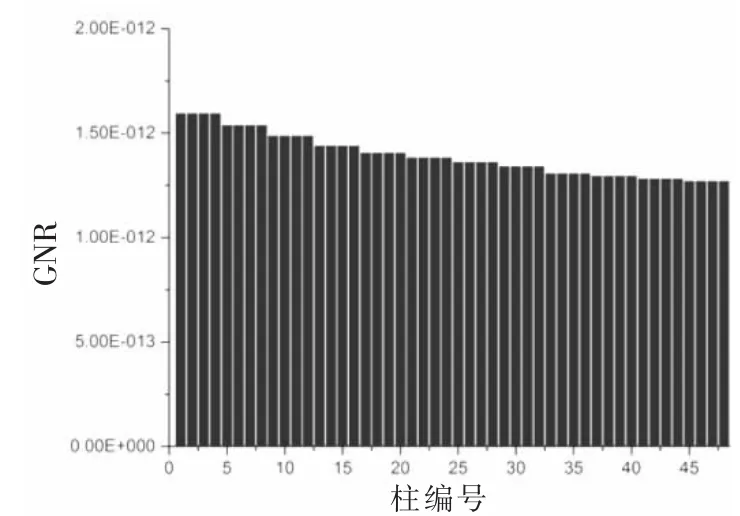
圖11 柱的GNR分布

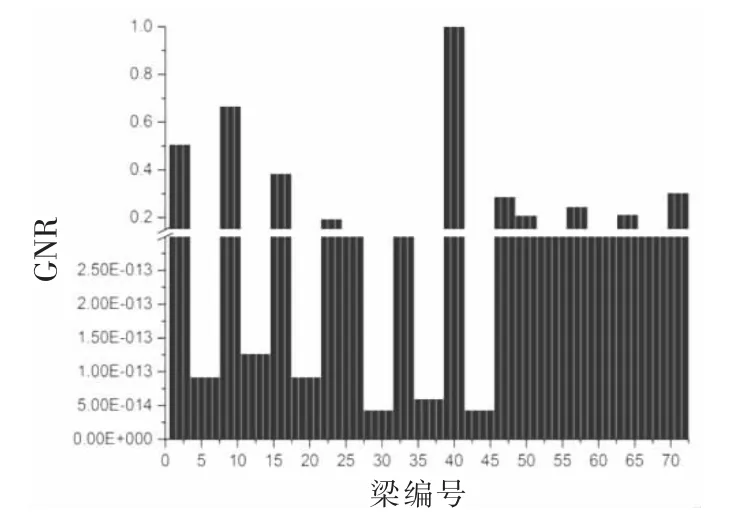
圖12 梁的GNR分布

3.2.2 彈塑性分析

圖13顯示了荷載位移曲線，此時針對的是水平荷載逐漸增大的情況。冗余延長率的評估見下表2。

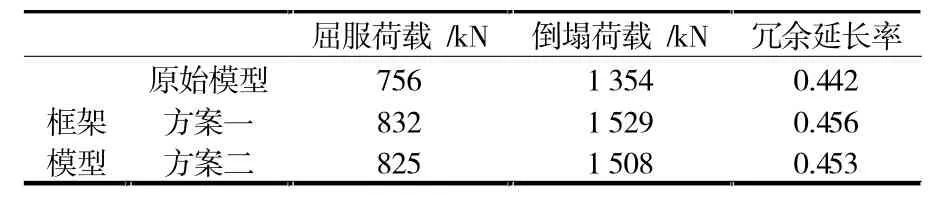
表2 框架模型冗余延長率評估

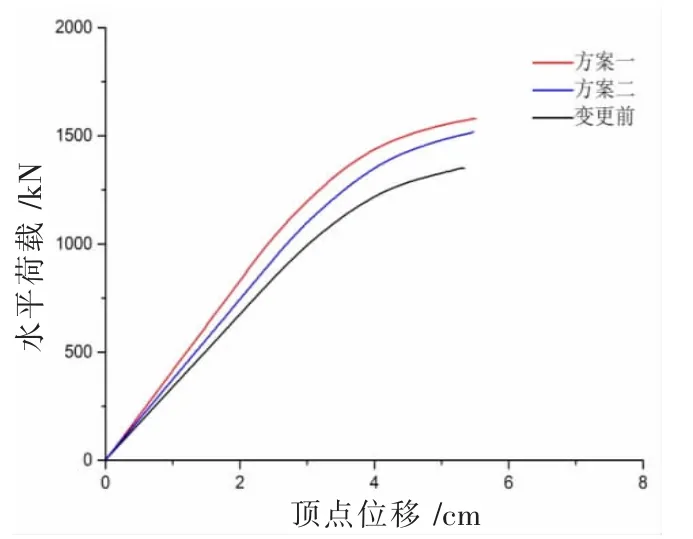
圖13 荷載位移曲線

由表2可知，優化后的方案一和方案二的模型結構的冗余延長率都得到了增加。三個模型的初始屈服點相近，崩塌荷載即極限荷載在優化后都有了明顯的提升。方案一優化后的冗余延伸率較方案二較高，而方案二優化后構件單元的冗余分布較方案一更加均勻，合理。縱觀微觀層面的柱梁冗余度和宏觀層面的冗余延長率，結構優化后都取得了較好的理論驗證。

4 結論

使用敏感性的冗余評估，根據冗余指標GNR分布和冗余延伸率等，可以通過改變結構尺寸對框架結構進行優化設計，得出以下結論：

（1）在框架模型中，施加在一個節點上的荷載由節點周圍的構件共同傳遞，所以許用應力比比較大的構件往往被認為是低冗余構件，如果周圍連接GNR值較小的部件，極易引起連續性倒塌；

（2）從余量均值的趨勢來看，由于框架結構具有較多不同方向的梁部件的存在，所以當某一個部件受到損傷時，對整體的影響較小；

（3）通過對結構的優化設計，可以改變部件的冗余特性，做到安全可靠的同時分配材料的性能使之更合理化；

（4）在彈塑性分析中，冗余延長率指標可以宏觀的看出結構的冗余特性，為優化結構設計提供對比驗證。