碳纖維布加固H型鋼梁的抗彎性能及承載力計算

郭 奧 楊勇新 賈 彬

(1.西南科技大學土木工程與建筑學院 四川綿陽 621010；2.中冶建筑研究總院有限公司 北京 100088)

隨著纖維復合材料產品的發展，大量纖維復合材料應用于土木工程領域，碳纖維復合材料從早期的碳纖維布或碳纖維板加固鋼筋混凝土結構到現在的混凝土中用碳纖維筋代替鋼筋并延伸到碳纖維加固鋼結構，應用范圍越來越廣[1]。我國現有的建筑中鋼結構占有很大的比重，但是很多鋼結構由于疲勞破壞或者環境腐蝕[2]，還未達到設計使用年限就發生破壞，造成鋼結構截面削弱，容易形成安全隱患。因此，對疲勞破壞或環境老化的鋼結構進行加固，延長其使用壽命達到預計的使用年限是需要解決的一個問題。

文獻[3-4]進行了碳纖維布(carbon fiber reinforced polymers,CFRP)加固鋼梁試驗，結果表明經過CFRP加固構件的極限承載能力顯著提高，而通過改變鋼梁底部CFRP的黏結層數，可以增加工字鋼梁承載能力的上限，但是剛度提高幅度較小。桂志光等[5]對碳纖維板與鋼板進行黏結剪切試驗，分析了剪切破壞過程與破壞機理，在有效黏結長度范圍內，兩種材料之間的極限黏結力隨碳纖維板的寬度增加而增大。國內外對于CFRP加固鋼結構的研究較多，主要通過試驗來驗證CFRP加固鋼結構的可行性，并未形成CFRP加固鋼結構設計理論，暫時沒有關于這方面的設計規范。本文對受彎鋼梁的受拉區底部粘貼CFRP布加固進行承載能力試驗，對比分析采用兩種長度CFRP和兩種層數的 CFRP布加固 H 型鋼梁的承載能力。

1 鋼梁加固試驗方案

本次試驗為驗證鋼梁經CFRP布加固后的效果，設計了4根試驗梁，鋼梁采用強度為Q235的鋼材，CFRP布和環氧樹脂的基本力學性能如表1。

表1 CFRP布和環氧樹脂基本力學性能Table 1 Basic mechanical properties of CFRP and epoxy resin

試驗所用鋼梁為HW125×125，如圖1(a)所示，鋼梁全長2 000 mm，兩端設置支撐，其凈跨為1 800 mm，截面尺寸為125 mm×125 mm×6.5 mm×9 mm，如圖1(b)所示，為防止在加載過程中發生傾覆，在加載點和支座處設置加勁肋。當采用碳纖維布加固H型鋼梁受彎構件時，在端部進行可靠的錨固措施，碳纖維端點處設置纏繞CFRP布和縱向CFRP布進行錨固，纏繞CFRP布寬50 mm，沿底部下翼緣纏繞至腹板距下翼緣50 mm處，一共設置3道間距為50 mm的纏繞CFRP布；腹板處縱向CFRP布對纏繞CFRP進行錨固，縱向CFRP布規格250 mm×50 mm。

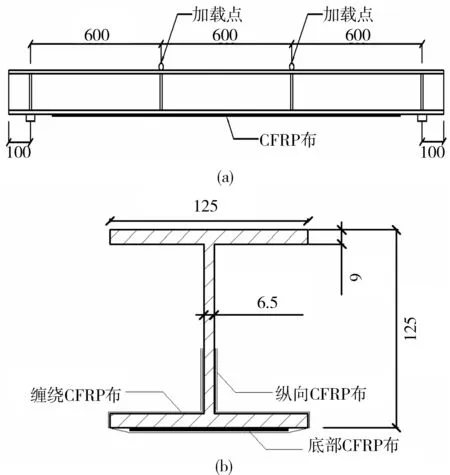
圖1 鋼梁及截面尺寸Fig.1 Section size of the steel beam

試驗采用4根梁，每根梁的尺寸均相同，其中1根無加固參照梁，3根加固梁。對鋼梁彎曲受拉區底部進行加固。CFRP布寬為100 mm，在受拉翼緣下部對稱布置，每根梁的編號以及加固方式見表2。

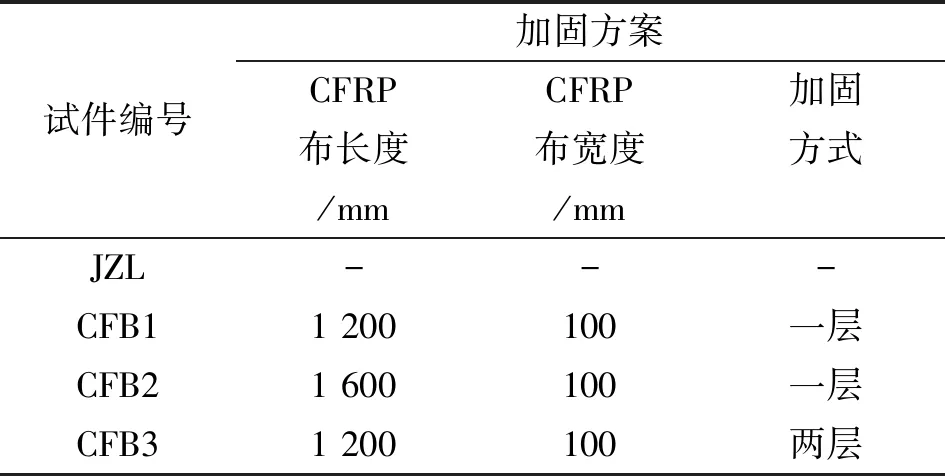
表2 試件編號和加固方案Table 2 Main parameters of the specimens

2 CFRP布加固鋼梁承載力試驗結果

2.1 試驗現象

對試驗鋼梁在加載前期采用10 kN/級逐級加載，接近屈服荷載時變小加載級數改為5 kN/級，荷載加載的過程中緩慢均勻，每級所加荷載的持荷時間為5 min，無明顯變化后再讀記各項測試數據，以保證加載鋼梁在荷載作用下的變形穩定[6]。

JZL為未加固梁，在試驗加載到試驗梁屈服荷載之前，JZL的跨中截面荷載和撓度變化呈線性關系。在達到屈服荷載以后，隨著荷載的增大，JZL撓度變化速率加快，有被壓彎的跡象。當加載的荷載值達到113.83 MPa 時，JZL的撓度突然加大，試驗構件破壞。

CBL1，CBL3 兩根梁的受力過程和破壞特征相似，在彈性狀態下試驗加載前期兩根梁的撓度變化仍然呈線性關系，但對比JZL的撓度可以觀察到用CFRP布加固后的鋼梁在相同荷載下撓度明顯減小，當試驗荷載值達到125.88 MPa 時，試件CBL1粘貼的CFRP布被拉斷，而當試驗荷載值達到136.74 MPa時，試件CBL3粘貼的CFRP布才被拉斷。

CBL2梁在前期撓度變形較小，荷載和撓度變形呈線性關系，相比CBL1梁在加固后的相同荷載下試件的撓度相比有減小，達到屈服荷載后，CBL2撓度變形加快，相比JZL和CBL1，加固提高了抗彎剛度。當加載到131.41 MPa時，CBL2的中CFRP布發生剝離破壞。

2.2 試驗結果

試驗梁的屈服荷載和極限荷載結果見表3，荷載-跨中撓度曲線如圖2所示。

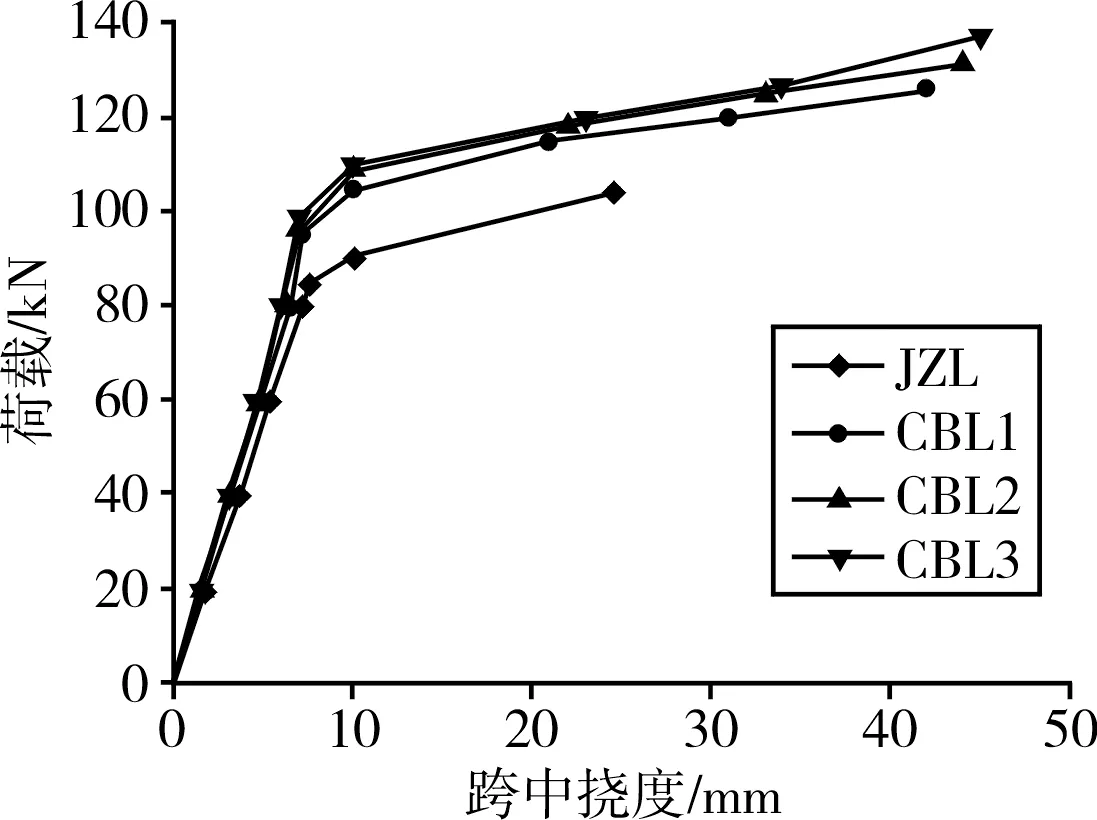
圖2 荷載-跨中撓度曲線Fig.2 Load-span deflection curve

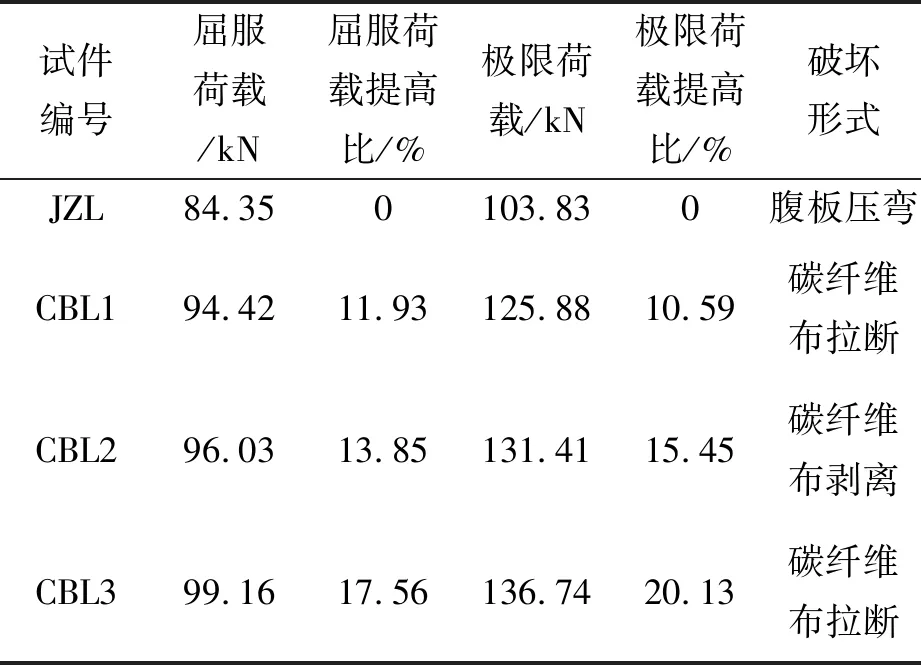
試件編號屈服荷載/kN屈服荷載提高比/%極限荷載/kN極限荷載提高比/%破壞形式JZL84.350103.830腹板壓彎CBL194.4211.93125.8810.59碳纖維布拉斷CBL296.0313.85131.4115.45碳纖維布剝離CBL399.1617.56136.7420.13碳纖維布拉斷

由表3可知，CFRP布加固鋼梁試驗中加固梁與參照梁相比，CBL1使用1 200 mm長的一層CFRP布加固鋼梁，其屈服荷載提高了11.93%，極限荷載提高了10.59%，CBL2使用1 200 mm長的兩層CFRP布加固鋼梁，其屈服荷載提高了13.85%，極限荷載提高了15.45%，說明CFRP布加固能提高鋼梁的承載能力，但增加CFRP布的層數對于承載能力的提高并不明顯，可能受到結構膠強度等影響，造成了CFRP布剝離而沒有充分發揮其高抗拉強度。CBL3使用1 600 mm的一層CFRP布加固鋼梁的屈服荷載提高了17.56%，極限荷載提高了20.13%，說明增加CFRP布的有效黏結長度能增加其承載能力的上限。試驗結果表明，采用性能良好的結構膠，使用有效加固長度的CFRP布在CFRP布加固鋼梁的工程應用中能充分發揮其性能。

3 CFRP布加固鋼梁正截面承載力計算

3.1 基本假定

對CFRP布加固鋼梁正截面承載力進行計算，本文對此進行以下假定：

(1)CFRP布加固鋼梁的截面滿足平截面假定；

(2)CFRP布與鋼梁之間的環氧樹脂均勻分布；

(3)鋼梁和CFRP布均為理想的彈塑性材料，鋼梁在達到屈服時，隨著應變的增加應力不變，應力-應變關系如圖3(a)所示，當εst≤εy時，有σst=Estεst；當εst>εy時，有σst=fy.

(4)CFRP布的線彈性應力應變關系如圖3(b)所示，σc=Ecεc.

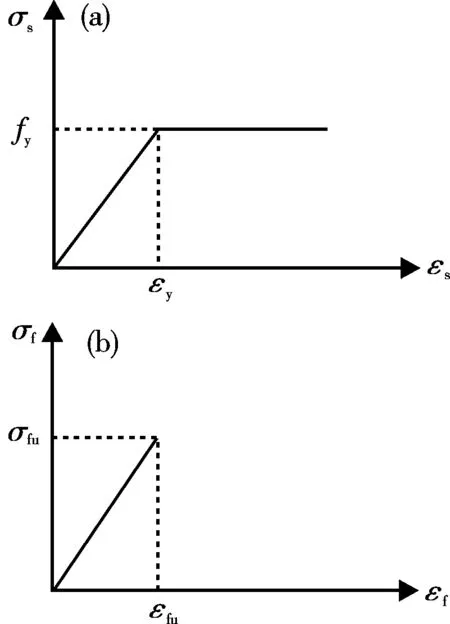
圖3 應力-應變曲線Fig.3 Stress-strain curves of steel and CFRP

3.2 CFRP布加固鋼梁受彎承載力公式推導

用CFRP布加固鋼梁之后，由于環氧膠已固化，CFRP布與鋼梁之間的黏結狀況良好共同受力。在彈性范圍內通過以上假定，加固之后構件滿足平截面假定，因此正截面的承載力分析可以用純彎曲梁正應力方法分析。在彈性范圍內梁內任意點的受力和變形與到中性軸的距離成正比，即橫截面上任意點的彎曲正應力與該點到中性軸的距離成正比：

(1)

式中：E為彈性模量；y為正截面上點到中性軸的距離；ρ為中性軸的曲率半徑。

圖4 鋼梁截面Fig.4 Section of the steel beam

在外加荷載作用下產生彎矩，有平衡關系式：

(2)

(3)

對式(2)、式(3)整理可得：

(4)

(5)

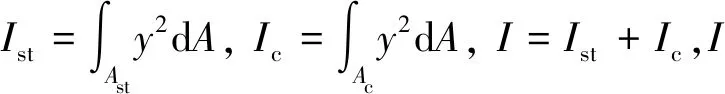
對慣性矩整理帶入式(5)，則有

(6)

將(6)帶入正應力計算公式得：

(7)

(8)

在CFRP布加固鋼梁的實際工程中，鋼梁和CFRP布的彈性模量已知，因此可以通過等強度的原理進行等截面代換，從而可以將CFRP換算成鋼材來計算截面的內力，對CFRP布的截面面積進行截面等效代換，計算CFRP布與鋼材兩種材料的彈性模量之比，CFRP的截面面積換算成鋼材的等效截面面積[7]，引入等效換算系數α(α=Ec/Est)，因此加固之后的等效面積A0為A0=Ast+αAc。

y0為換算截面中和軸到受壓邊緣的距離，可根據梁的受壓區和受拉區對中和軸的面積距相等來計算[7]，則有：

(9)

(10)

式中h為鋼梁的截面高度。則有換算截面的慣性矩：

(11)

其中I為鋼梁截面中性軸慣性矩。

CFRP布加固鋼梁截面正應力可按鋼材的換算截面的計算公式來進行計算，其計算公式為：

(12)

最大正應力一般在彎矩值最大處，且為距離中性軸最遠點，從式(12)可知，正應力大小與彎矩值和y/I0有關，用W1=I0/y0和W2=I0(h-y0)表示鋼梁受壓區邊緣和受拉區邊緣的抗彎抵抗矩，帶入正應力公式，w2=I0(h-y0)鋼梁受壓區邊緣的正應力為 ：

(13)

鋼梁受拉區邊緣的正應力為：

(14)

CFRP布的正應力為：

(15)

鋼梁最大主平面承受橫向荷載或彎矩作用時，當荷載達到一定數值時，梁有可能發生側向彎曲和扭轉，而發生整體失穩破壞。對于CFRP布加固鋼梁，也應該驗算其加固梁的整體穩定。

(16)

式中,W1為按受壓翼緣所確定的換算截面抵抗矩，A0為鋼梁和CFRP布的換算截面面積，ηb為截面不對稱系數，其余各參數含義及計算方法同《鋼結構設計規范》。

式(13)、式(14)、式(15)即為在彈性階段的彎矩作用效應下CFRP布加固鋼梁的正截面承載力計算公式。本文公式的推導是在假定下進行彈性范圍內的計算，用于后期的試驗數據進行驗證分析，還需補充彈塑性階段的理論計算公式為定量設計作理論指導。

4 結束語

本文通過對比采用不同長度和不同層數的CFRP布加固鋼梁得出以下結論：(1)采用CFRP布加固的鋼梁，其承載能力有明顯提高，CFRP布的黏結長度增加能提高承載能力，因此對于用于鋼梁的CFRP布需要有足夠的有效黏結長度。(2)增加CFRP的加固層數對于其承載能力的提高并不明顯，需要進一步驗證增加層數的有效性。(3)在設計中CFRP布加固鋼梁的計算公式需要繼續完善，在實際工程中需要考慮施工工藝對加固效果的影響，并且對CFRP布的端部錨固需要繼續深入研究。