CunZn(n=1～12)團簇結構和性質的第一性原理研究

馮江平 鄺向軍

(西南科技大學理學院 四川綿陽 621010)

雖然人們對于銅鋅混合團簇以及Zn摻雜Au,Ag,Cu團簇有了很多研究[7-9]，但迄今為止還沒有對雙金屬CunZn(n=1～12)團簇進行系統性的理論研究。它們的鍵長和價鍵的功能仍然是未知的，其幾何結構和特性是否與純銅團簇的幾何結構和特性存在很大的不同？因此，需要了解CunZn(n=1～12)團簇的幾何結構和能量結構等。本文基于密度泛函理論，在GGA-PW91交換關聯勢上對CunZn(n=1～12)團簇進行全電子標量相對論(AER)研究，重點研究雜質Zn對小銅團簇的幾何結構、能量結構和相對穩定性的影響，對于全面了解銅鋅團簇的結構和性能具有積極意義。

1 方法和模型

本文使用了基于密度泛函理論原理的計算軟件包 Dmol3,參數選取了廣義梯度近似(GGA)中的PW91交換關聯勢，使用了雙數值基組(DNP)和全電子相對論贗勢,明確包含所有電子，并將相對論效應引入核心，這樣盡管計算成本最高，但卻是最精確的。自洽場的能量收斂標準為1.0-6u，為了更快地計算，將拖尾數值設置為0.005 Ha。而在結構優化過程中，最大力設置為0.002 Ha/?(1 Ha=27.211 eV,1 ?=0.1 nm,下同)，最大位移設置為0.005 ?，最大能量設置為1.0-5Ha，同時設置了自旋和結構對稱性不受限制且多重態自選。此外，通過在相同理論水平上計算諧波振動頻率，確定了優化幾何的穩定性，沒有任何虛頻。

初始幾何形狀的選擇對所獲得的最低能量結構的可靠性很重要，在這項工作中，我們將通過以下方式獲得初始結構。首先，參考對銅團簇結構的已有研究，對銅團簇進行了優化，獲得了銅團簇的最低能量幾何結構。然后，通過用Zn原子替代Cun+1團簇所有非等價位一個Cu原子或通過直接添加Zn原子在Cun團簇的每個可能的非等價位上來獲得CunZn團簇的初始結構，對于其它的不同結構也選取了多種進行了計算。

為了檢驗計算方法的可靠和準確,采用不同的交換關聯勢來計算Cu2團簇并與實驗結果相比較，表1是在相對論贗勢下選取幾種不同的交換關聯勢計算所得Cu2團簇的鍵長、結合能，也給出了實驗值。從表1可以看出用PW91-GGA交換關聯勢來計算Cun團簇體系最為恰當，因為計算得到Cu2團簇的鍵長2.222 ?，結合能2.22 eV與實驗值[10]2.219 3 ?，2.01±0.08 eV符合最好。我們也使用相同的方法計算了Zn2團簇的鍵長為3.14 ?，這與實驗值[11]3.18 ?較一致，因此，我們所使用的計算參數對CunZn團簇的研究是可靠和準確的。

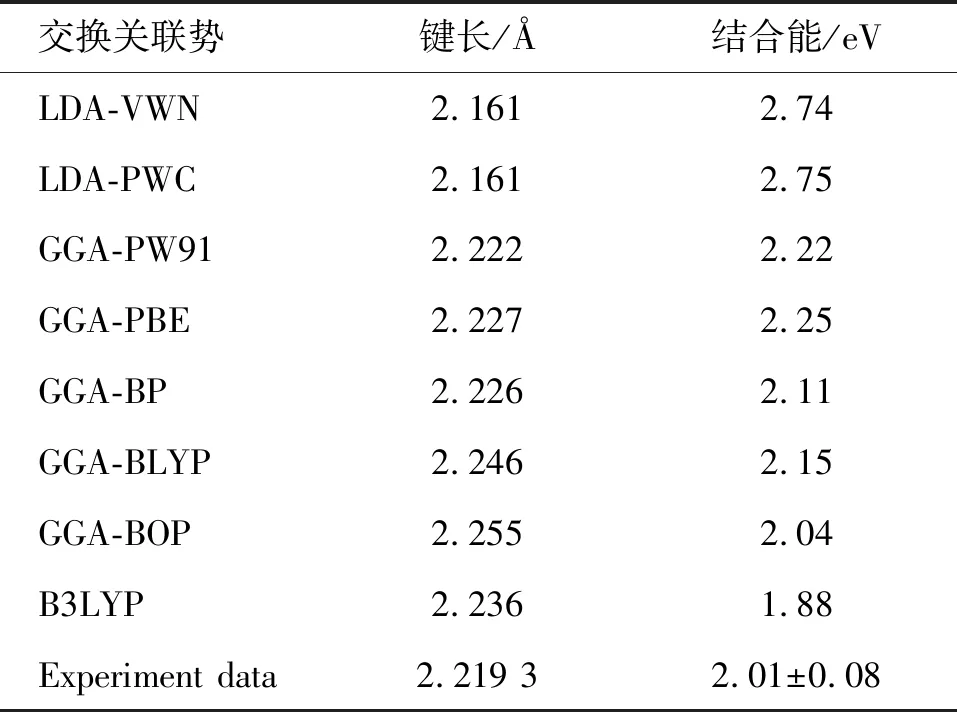
表1 Cu2團簇在不同交換關聯勢下計算的鍵長與結合能的結果比較Table 1 Result comparison between bond length and binding energy of Cu2 clusters under different commutative correlation potentials

2 結果與討論

2.1 幾何結構

在Cu5Zn團簇的情況下，優化的基態幾何結構不同于純銅Cu6團簇，它不是一個平面結構，而是一個三維結構，對稱性為D4v，它是由在Cu6團簇的異構體上用一個Zn原子替換一個Cu原子得到。而Cu5Zn團簇的更高能量結構是具有C2v對稱性的平面結構，由Zn原子取代Cu6團簇基態結構中二配位位置的銅原子獲得。能量更高的異構體是采用不同的高對稱結構和在基態Cu5團簇上添加一個鋅原子得到，對稱性為C2v,C1。

Cu9Zn團簇的最低能量結構是在Cu9團簇上添加一個銅原子產生，具有Cs對稱性。通過替換Cu10團簇中的一個銅原子而獲得更高能量的具有C1對稱性的異構體。Cu12Zn團簇類似于Cu9Zn團簇，它的基態結構是Cu12團簇的基態結構右邊增加Zn原子產生，具有C1對稱性。它的更高能量的異構體是用鋅原子取代傳統的高對稱性結構中的銅原子得到，具有較高的C5v,Ih對稱性。

圖1 純Cun+1(n=1～12)團簇，CunZn(n=1～12)團簇的優化幾何結構注：CuCu，CuZn鍵(長度以埃(?)為單位)，對稱性和最低能量結構與其異構體之間的能量差異顯示在每個團簇結構的旁邊。Fig.1 Optimized geometry of pure Cun+1 (n=1-12) clusters, CunZn (n=1-12) clusters

2.2 能量結構

為了深入了解CunZn(n=1～12)團簇的物理和化學性質，計算了Cun+1團簇和CunZn團簇的平均結合能和垂直電子親和勢，如圖2所示。以下是我們對平均結合能和垂直電子親和勢的定義：

平均結合能：

Eb(Cun+1)=[(n+1)E(Cu)-

E(Cun+1)]/(n+1)

(1)

Eb(CunZn)=[nE(Cu)+E(Zn)-

E(CunZn)]/(n+1)

(2)

垂直電子親和勢:

VEA(Cun+1)=E(Cun+1)-E(Cun+1)-

(3)

VEA(CunZn)=E(CunZn)-E(CunZn)-

(4)

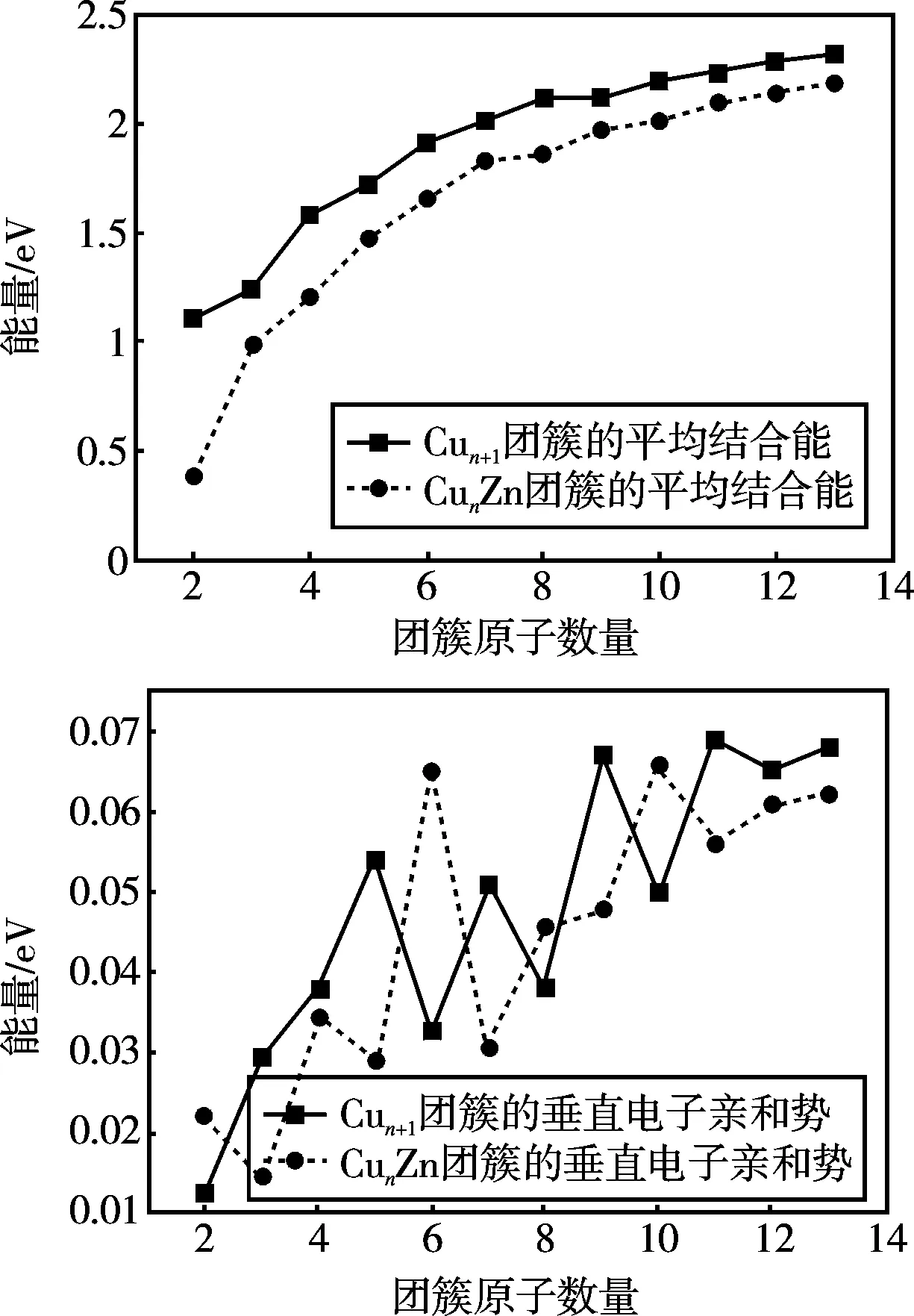
圖2 Cun+1團簇和CunZn團簇的平均結合能和垂直電子親和勢隨團簇尺寸的變化關系Fig.2 Size dependence of the average binding energy and VEA of pure Cun+1 clusters and CunZn clusters

一般而言，給定團簇的平均結合能是其總熱力學穩定性的量度。根據圖2，Cun+1團簇的平均結合能大于相應的CunZn團簇。隨著團簇尺寸的增大，純銅團簇和CunZn團簇的平均結合能逐漸增大，而CunZn團簇與相應的Cun+1團簇之間的平均結合能差隨著團簇增大而越來越小，這表明了在摻雜Zn原子后降低了團簇的整體穩定性，而團簇的總熱力學穩定性隨團簇增大而增大的趨勢并沒有改變。隨著團簇數量變多，Zn原子對它的總熱力學穩定性的作用也越來越小。當n趨近于無窮時，就相當于銅晶體的情況，這時平均結合能收斂于3.4 eV。

垂直電子親和勢(VEA)是用來評估不同粒徑團簇化學穩定性的一種手段。較高的垂直電子親和勢意味著當將電子添加到中性分子時釋放更多的能量，并且相應的陰離子的產生更容易實現。具有較小垂直電子親和勢的中性團簇通常更具化學穩定性。如圖2所示，偶數CunZn團簇的VEA比相應的偶數Cun+1團簇要小。而與之相反的是，奇數CunZn團簇的VEA通常比對應的奇數Cun+1團簇大或者相近。根據VEA的含義，奇數CunZn團簇化學穩定性和電子穩定性一般高于相應的奇數Cun+1團簇。也就是說，通過摻雜Zn原子，相對活潑的偶數Cun+1團簇變成化學穩定性和電子穩定性較高的偶數CunZn團簇，相對穩定的奇數Cun+1團簇變成相對不穩定的奇數CunZn團簇。

3 結論