利用剪應力公式研究楔形截面梁的彎曲正應力

吳 曉

（湖南文理學院?機械工程學院，湖南?常德?415000）

楔形截面梁在空間結構中應用比較廣泛。文獻[1]討論了兩端固支楔形變截面梁的熱彎曲，文獻[2]采用求積元法分析了楔形變截面鋼-混凝土組合梁彎曲和自由振動，文獻[3]研究了剪力對楔形變截面雙模量梁彎曲應力的影響，文獻[4]研究了考慮剪切效應的旋轉FGM從楔形梁剛柔耦合動力學建模與仿真，文獻[5]研究了用楔形體解答求解矩形變截面梁及其適用范圍，文獻[6]研究了楔形梁腹板在彎、剪及局壓聯合作用下的彈性屈曲，文獻[7]研究了交叉梁系結構中變截面桿件的計算問題。由以上文獻可知，楔形梁是實際工程中較常見的承載構件。彈性理論采用半逆解法研究楔形梁的彎曲應力是采用多項式進行求解的，存在一題一方法一解的不足，且不能求解復雜外載荷作用下楔形梁的彎曲應力。本文利用剪應力公式研究了楔形梁彎曲正應力的求解，得到了復雜外載荷作用下楔形梁的彎曲正應力公式，彌補了彈性理論的不足。

1??楔形梁彎曲正應力

對于圖1所示復雜載荷作用下的楔形梁，可用奇異函數把外載荷表示為如下載荷集度形式：

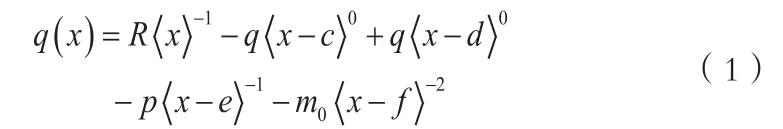
把式（1）對x積一次分可得梁截面剪力：

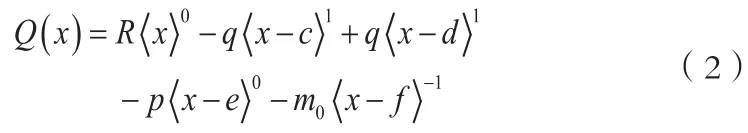
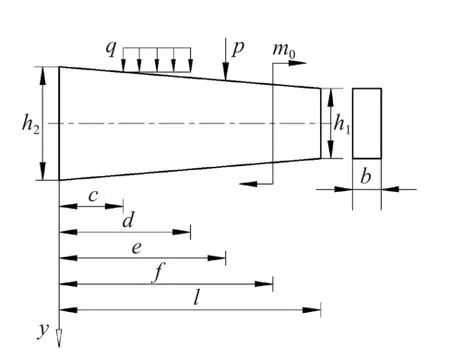
圖1 復雜載荷作用下楔形梁

把式（2）對x積一次分可得梁截面彎矩：

對于圖1所示楔形梁，可把其截面高度表示為：

式（4）中：

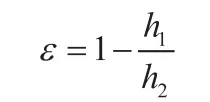
利用式（4）可知楔形梁截面慣性矩及靜矩分別為：

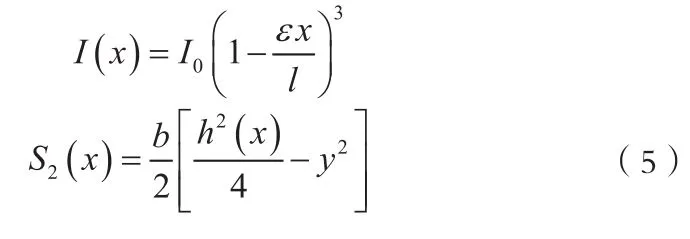
由材料力學可知，圖1所示楔形梁截面剪應力近似公式為：

由文獻[8]可知，采用式（6）計算楔形梁截面剪應力已不適用，但是可利用式（6）求得計算復雜外載荷作用下楔形梁截面通用彎曲正應力修正公式。

由文獻[9]可知有下式成立：

式（7）中：G為剪切彈性模量；u為軸向位移；u（0）為中性層軸向位移；w為楔形梁彎曲撓度。

利用式（4）～式（7）可得：

把式（1）～式（3）代入式（13）中即為圖1所示復雜載荷作用下，楔形梁彎曲正應力修正公式，此彎曲正應力修正公式是通用公式。而彈性理論僅能對單一載荷給出一題一解，存在一定的局限性。

2??算例分析

為了檢驗式（13）的計算精度，下面以圖2所示集中載荷作用下懸臂楔形梁為例，進行計算。

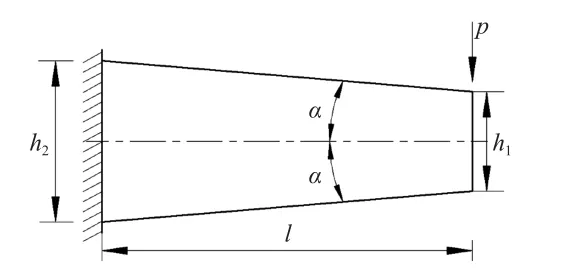
圖2 集中載荷作用下楔形梁

由文獻[8]、文獻[9]可知，h1=0時，圖2所示懸臂楔形梁在集中載荷作用下截面最大正應力為：

下面把β、β’隨半楔角α變化的數值列在表1中，以便討論分析。

表1 β、β’的數值（μ=0.25）

由表1可知，本文方法式（16）的計算結果與彈性理論式（17）的計算結果在半楔角α≤ 40°即楔形角度不超過80°范圍內吻合得比較好，式（16）與彈性理論式（17）計算誤差均沒有超過實際工程所允許的誤差5%。在工程實際中，半楔角α=40°的楔形梁已經是很少見的了。

彈性理論式（17）僅是圖2所示懸臂楔形梁當h1=0時的解析解，而本文給出的式（13）、式（15）則是圖1所示在復雜載荷作用下楔形梁的彎曲正應力公式，所以說本文給出的楔形梁彎曲正應力修正公式是通式，本文方法彌補了彈性理論存在一題一方法一解的不足。

3??結論

（1）本文方法給出的楔形梁彎曲正應力修正公式的計算結果與彈性理論方法的計算結果，在半楔角α≤40°即楔形角度不超過80°范圍內吻合得比較好，計算誤差均沒有超過實際工程所允許的誤差5%。這說明本文方法給出的楔形梁彎曲正應力修正公式計算精度較高。

（2）本文給出的楔形梁彎曲正應力修正公式是通式，對任意載荷作用下楔形梁的彎曲應力計算都適用，而彈性理論的半逆解法僅適用楔形梁在單一載荷作用下的彎曲應力計算，本文方法克服了彈性理論一題一方法一解的局限性。