基于Lorenz混沌同步系統的未知頻率微弱信號檢測

李國正， 譚南林， 蘇樹強， 張 馳

(北京交通大學 機械與電子控制工程學院, 北京 100044)

微弱信號是指深埋在背景噪聲中的極其微弱的有用信號，如弱光、微溫差、微振動、弱磁、微電流等。檢測微弱信號在航空航天[1]、故障診斷[2]、生物醫學[3]、通信傳輸[4]、系統辨識[5]等領域有著及其廣泛的應用。隨著科學技術的發展，對微弱信號的檢測，越來越受到重視，需求量日益增加。該項技術的進步對相關行業的發展會產生深遠影響，具有重要意義。將淹沒在強噪聲背景下的微弱信號快速、準確的檢測出來是信號處理領域的熱點問題，受到國內外學者的廣泛關注。

傳統微弱信號檢測方法多基于線性系統，這使得有用信號被放大的同時，背景噪聲也隨之放大，而采用濾波器濾去噪聲的同時，信號會有所損失。混沌類微弱信號檢測方法基于非線性系統，充分利用了混沌系統具有的初值敏感性、噪聲免疫性和非線性放大特性來實現信號檢測，可以檢出信噪比低至的微弱信號。此類方法自20世紀90年代提出后，很多學者對此展開了深入的研究[6]，該方向成為了混沌理論應用于實際工程的研究熱點之一。

現階段的研究主要集中在以下四個方面：一是對混沌系統檢測機理的分析和探討。代表性的研究有：王永生等[7]研究了數值解算時計算步長和驅動輸入白噪聲對弱信號檢測中Duffing振子運動特征的影響。吳彥華等[8]研究了待檢信號與Duffing系統內置信號頻差和相差對系統相圖的影響，提出了微弱信號盲檢測識別算法，建立了檢測模型。孫文軍等[9]研究了Van der Pol振子相態躍遷模型，從理論上證明了其用于弱信號檢測的可行性，并與Duffing振子進行了對比分析。二是對混沌系統相空間運行軌跡計算和運行狀態判定方法的研究。其中，Rashtchi等[10]提出通過計算相空間軌跡自相關系數判斷狀態轉變的方法，并與最大Lyapunov指數法進行了比較。Awrejcewicz等[11]利用Melnikov法預測了非線性系統振子在微作用力下系統自由度的改變，并通過數值仿真證明了該結論；三是對構建檢測系統應用于工程實際方面的研究。其中，溫宇立通過數值模擬和實驗研究,驗證了Duffing混沌系統的相軌跡識別多裂紋管道超聲導波信號的有效性。Zhao等[12]結合混沌和倒譜分析的方法對液壓試驗機梭閥的早期故障進行診斷。張偉偉等[13]提出一種基于改進型Duffing混沌振子系統的強噪聲下超聲導波的識別和定位方法，并利用導波信號對系統相軌圖的顯著變化識別導波信號。陳志光等[14]研究了強海洋背景噪聲下微弱周期信號的檢測，提出利用希爾伯特變換實現對間歇混沌的包絡檢測的新方法。四是對頻率未知微弱信號檢測方法的研究。其中，李國正等[15]提出了構建Duffing振子陣列，結合遺傳算法尋找輸入信號后相空間方差最大值所對應的頻率量，以實現頻率估計的方法，以及基于蔡氏電路構建的混沌同步系統進行待測信號參數估計的方法[16]。孫自強等[17]采用取樣積分技術提高混沌振子對增速箱振動故障信號的檢測門限,利用混沌振子相圖變化實現齒輪早期故障診斷。

上述研究表明，利用混沌系統的相關特性進行微弱信號檢測可以極大消除背景噪聲的影響，進而提升被測信號的信噪比，降低檢測門限，是很有潛力的微弱信號處理技術。但上述方法受參數設定、相空間軌跡求解、運行狀態判定等因素的影響，仍存在檢測效率偏低、狀態轉換易誤判等不足。尤其對未知頻率的周期信號進行檢測時，基于間歇混沌現象或基于優化算法的檢測方法所采用的混沌系統陣列結構非常復雜，需要在整個頻域區間內掃描估計，且難以處理含有多個周期信號的被測對象，這大大影響了它的適用性。

為此，本文首先從典型Lorenz系統的信號檢測機理展開研究，采用驅動-響應法構建基于混沌同步方式的微弱信號頻率檢測系統。再結合MUSIC(Multiple Signal Classification)算法處理降噪后得到的同步誤差，實現頻率估計。最后，采用建立的模型進行對比試驗，驗證其可行性。新方法綜合利用了混沌系統的初值敏感性、抗噪性、非線性放大性和同步性，從而簡化系統參數設定，避免相空間軌跡復雜求解，提高了檢測效率。

1 系統模型與頻率估計

1.1 頻率檢測系統模型和工作機理

本文提出的新方法所檢測的對象是強噪聲背景下微弱周期信號的頻率值，其表達式為：

r(t)=s(t)+n(t)

(1)

式中，s(t)是微弱正弦信號Asin (ωt+θ)，n(t)是白噪聲信號N(0,σ2)。該信號信噪比小于-20 dB，對頻率值ω進行估計。

考慮到現有混沌類檢測方法基于單一混沌系統進行檢測時仍未解決的諸多難點問題，本文提出引入一個新的具有相同結構和參數的混沌系統，利用兩個混沌系統之間可以同步運行這一特性，結合MUSIC算法，來實現微弱信號的頻率檢測。該頻率檢測系統的原理性框圖，如圖1所示。

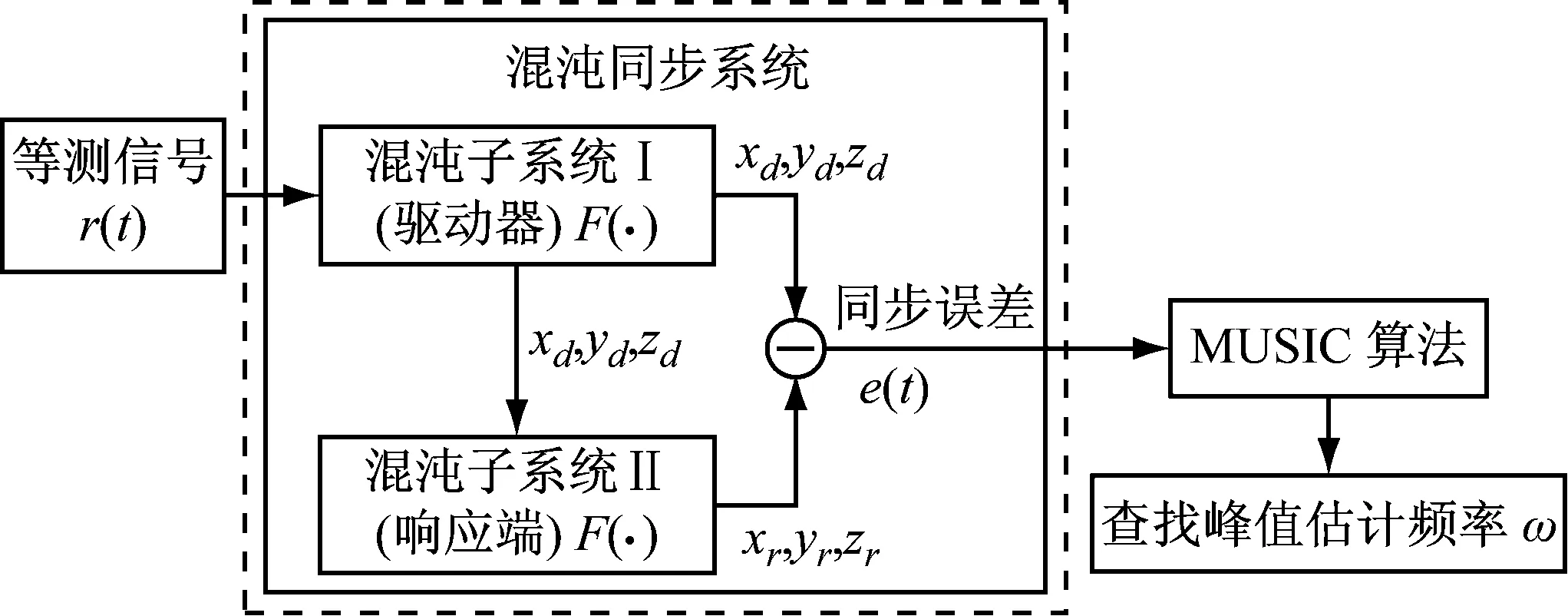
圖1 混沌同步頻率檢測系統原理圖

圖1中，混沌子系統I作為同步系統的驅動端，混沌子系統II作為響應端，二者之間采用驅動-響應法實現同步。當待測信號接入驅動端后，引發其相空間運行軌跡發生了巨大改變。受混沌系統的初值敏感性和噪聲免疫性的影響，驅動端放大周期信號的同時，對背景噪聲產生抑制作用。而響應端的相空間軌跡作為對比，可得到同步誤差e(t)，以此評估輸入信號后相空間軌跡產生的變化。MUSIC算法作為空間譜估計測向理論的重要算法，進一步消除噪聲所產生的影響。用其處理同步誤差，查找空間譜峰值，最終實現頻率估計。

1.2 Lorenz系統及參數設定

現有混沌類檢測方法大多基于單個Duffing振子搭建系統。該系統內包含一個周期策動力。測量不同頻率的周期信號時，需要對其策動力參數進行調整，或是采用陣列結構覆蓋整個需要檢測的頻率區間，這大大增加了構建難度。Lorenz系統由麻省理工大學教授Lorenz首次提出，是一個常微分方程組，在某些參數值和初始條件有混沌解[18]。其數學模型如下

(2)

式中，r(t)是接入的被測信號，它在典型的Lorenz系統中并不存在，此時系統轉換成為一個更高維的非線性動力學系統。對該模型的動力學特性進行研究，取結構參數為：σ=10,β=2.6。改變參數ρ的取值，得到系統的分岔圖，如圖2所示。

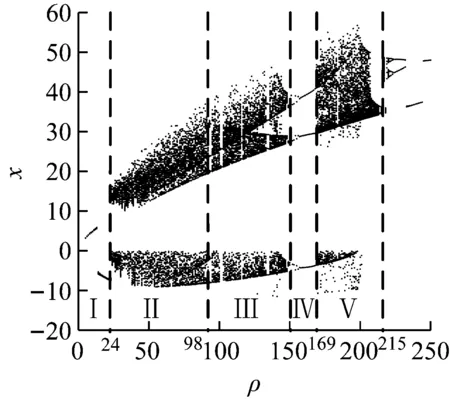
圖2 參數ρ的分岔圖

圖2中，參數ρ的取值范圍為[0,250]。隨著參數值增加，系統的運行狀態在多周期態和混沌態之間變換。狀態轉化的臨界點有24、98、150、169、215，可以據此劃分成6個子區間。其中，區間I、IV和VI內，系統運行在多周期態；區間II內，運行在混沌態；區間III內，主要為混沌態，特定數值出現多周期態。進一步分析系統處于不同狀態時，輸入信號對相空間運行軌跡的影響。取ρ=169和ρ=50，并輸入不同類型的待測信號，得到的相空間軌跡如圖3所示。

圖3的相空間軌跡包含有四條曲線，曲線a是輸入信號r(t)=0時得到，曲線b是r(t)=0.001sin(t)時得到，曲線c是r(t)為方差等于0.001白噪聲時得到，曲線d是由曲線b中的正弦信號疊加曲線c中的白噪聲信號得到。圖3(a)中，系統運行在三周期態，四條曲線的運行軌跡在相空間內幾乎完全重合，難以區分，無法應用于信號檢測。圖3(b)中，系統運行在混沌態時可以看出，在非線性系統的作用下，曲線a和曲線c非常接近，而曲線b和曲線d也保持基本一致，而曲線a和c與曲線b和d相比，系統的運行軌跡則發生了巨大的偏移。

為了進一步分析不同參數條件下輸入信號對相空間運行軌跡產生的影響，逐步增加Lorenz系統的參數ρ，同時獲取上述四種信號輸入時系統的運行軌跡。以此計算正弦信號輸入、白噪聲輸入、正弦信號疊加白噪聲輸入時空間軌跡相對于無測試信號輸入時運行軌跡的偏移量，繪制其與參數值ρ之間的關系曲線，分別對應于曲線a、b和c，如圖4所示。

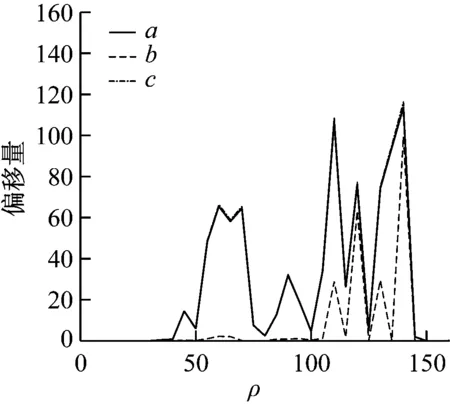
圖4 參數ρ與軌跡偏移量之間的關系曲線

結合圖4、與參數ρ的分岔圖可以看出，不同信號輸入時，軌跡偏移量的大小除了與信號種類相關外，還與ρ的取值使系統所處的運行狀態有關。當ρ的取值在圖2中對應的區間I和IV內時，系統運行在多周期態，三種輸入信號對應的偏移量小；取值在區間III內時，系統在混沌態和多周期態之間切換，三種輸入信號對應的偏移量波動劇烈；取值在區間II內時，系統運行在混沌態，輸入信號中的白噪聲使系統的相空間軌跡在原有運行軌跡的周圍發生小幅抖動，而周期信號則使得空間軌跡產生了很大的偏移，且該偏移量遠大于輸入信號的幅值。當參數ρ在此區間內時，適用于信號檢測中的降噪處理。如果能夠獲取輸入信號前后相空間軌跡發生的變化，則可以從其偏移量對相關參數進行估計。

1.3 Lorenz混沌同步系統

參照圖1的系統框架，基于Lorenz系統，采用驅動-響應法構建同步系統。驅動端混沌子系統I的狀態方程是

(3)

響應端混沌子系統II的狀態方程是

(4)

可以證明，當混沌系統中的參數滿足條件σ>0和β>0，且輸入信號r(t)=0，子系統I和II可以實現同步。

為了證明上述結論，構建Lyapunov函數如下式

(5)

對其求導可以得到

(6)

結合假定條件r(t)=0，并用式(3)減去式(4)，可以得到下式

(7)

代入式(6)，可以得到

(8)

顯然，結構參數σ>0,β>0，時，上式小于0。根據Lyapunov穩定性定理可知所建立的系統的同步誤差在零點位置漸進穩定，上文子系統I和II同步的相關結論成立[19]。

1.4 MUSIC算法與頻率估計

當輸入信號r(t)作為擾動項接入所建立的同步系統后，會出現同步誤差。根據上文分析可知，同步誤差主要受到輸入信號中周期信號成分的影響而產生，由此推斷同步誤差的信噪比與被測信號相比會有極大改善。MUSIC算法是Schmidt提出的一種基于矩陣特征空間分解的方法[20]，是空間譜估計測向理論的重要基石。很多學者對該算法的效率、敏感度等方面展開了研究和分析，結果表明該算法可以有效減少噪聲的影響，準確估計信號頻率。我們采用該算法對同步誤差進行處理，基本流程如下：

步驟1將同步誤差e(t)作為變量X，取延時變量為T，獲取新的同步誤差序列e(t+T)作為變量Y。變量X和Y包含有L個數據。

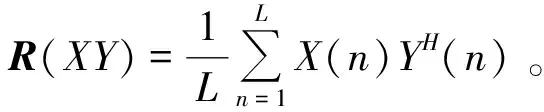
步驟3對矩陣R(XY)進行特征分解，得到其特征值λ1,λ2,…,λM以及特征向量υ1,υ2,…,υM。將特征值由大到小排列，取前d個對應的特征向量，構建信號特征矩陣US=[υ1,υ2,…,υd]。剩下的特征向量構建噪聲特征矩陣UN=[υd+1,υd+2,…,υM]。

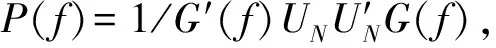
步驟5查找空間譜的峰值，其對應的頻率值即為被測信號頻率的估計值。

為了檢驗該方法的有效性，進行了兩組試驗。取Lorenz系統參數為σ=10,β=2.6和ρ=50，此時系統處于混沌態。將正弦信號0.001sin(2πt)與白噪聲(N(0,0.05))疊加，作為輸入信號接入該系統，其信噪比為

SNRr(t)=10lgPs(t)/Pn(t))=-50 dB

(9)

再將正弦信號的頻率變為50 Hz，保持信噪比不變并接入該系統。兩次同步誤差計算得到的空間譜，如圖5所示。

由圖5可知，淹沒在強噪聲背景中的正弦信號的頻率值可以從同步誤差的空間譜中準確得到。圖中的多條曲線是以被測信號的周期長度為基本單位，取其1倍～10倍長度的同步誤差數據，用MUSIC算法計算得到。可以看出隨著數據長度的增加，頻率估計值不斷逼近實際值。當長度為被測信號周期長度的4倍時，得到的頻率值分別為0.99 Hz和49 Hz，與實際值基本一致。

2 系統檢測特性分析

2.1 幅值與頻率的檢測范圍

接入的被測信號使Lorenz系統的相空間軌跡出現擾動，進而對其運行狀態產生影響。為此，需要對被測信號幅值與頻率的有效檢測區間進行分析。我們采用維持Lorenz系統的結構參數不變，獲取輸入信號幅值A的分岔圖，以及維持被測信號信噪比不變，獲取同步誤差信噪比的變化曲線的方法分別進行研究。結果如圖6所示。

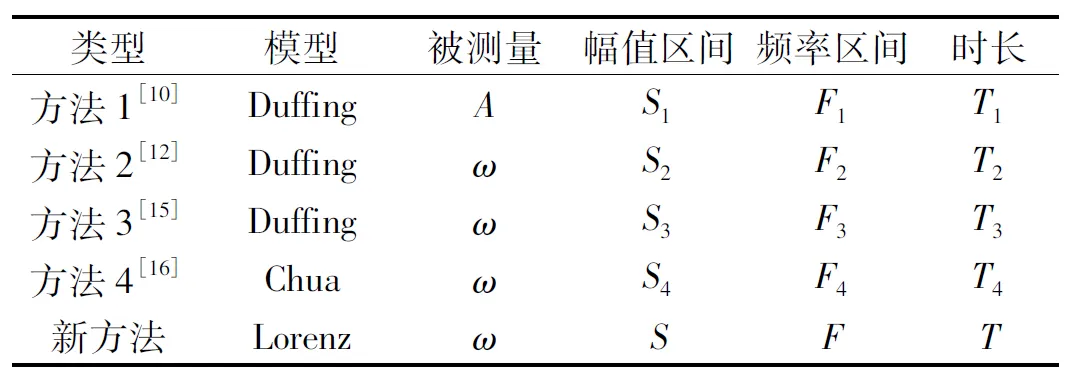
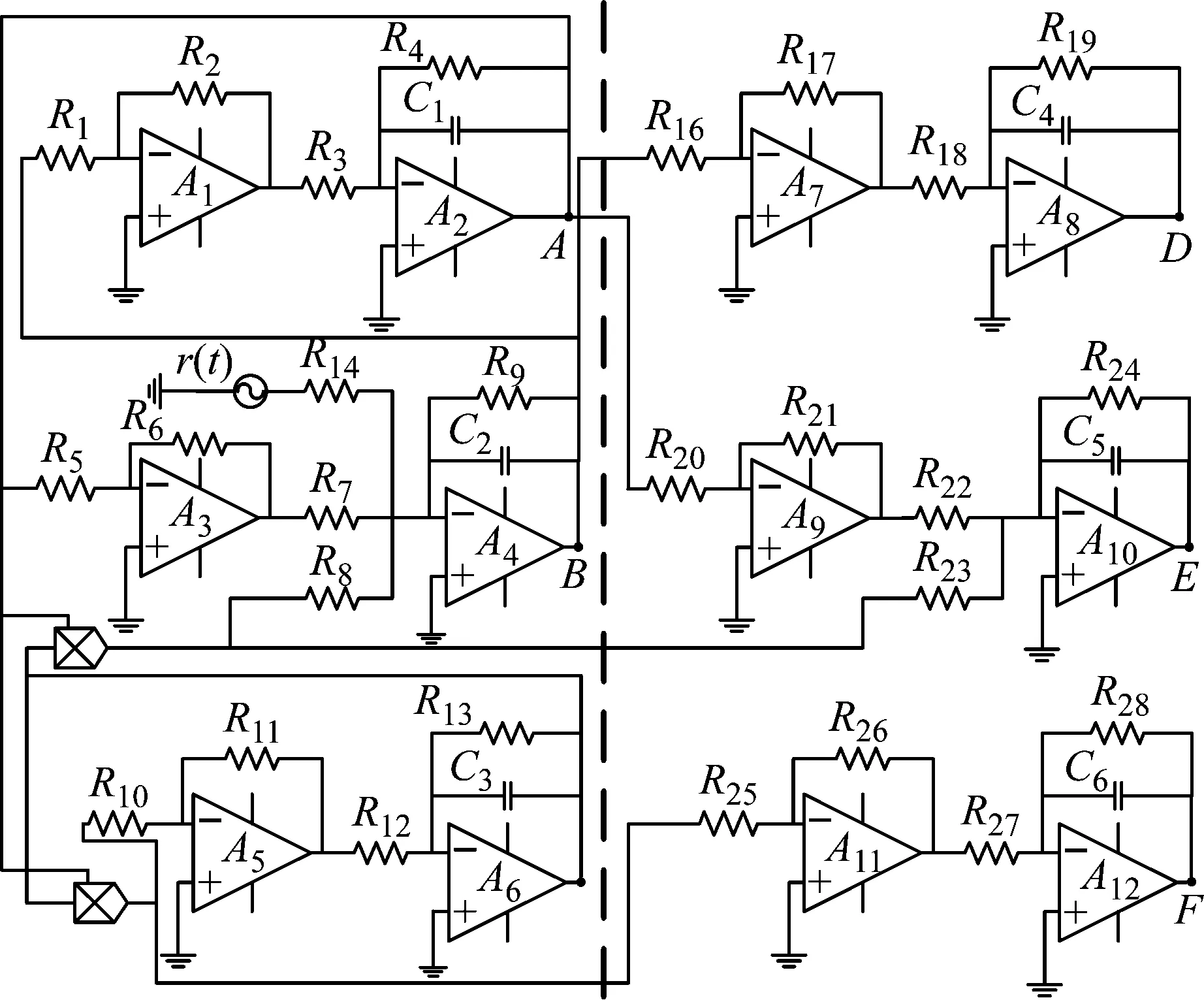
圖6(a)可以看出，引入的待測信號改變了Lorenz系統的原有動力學特性。當幅值為45、104和167時，系統處于狀態轉化的臨界點。根據前文的分析可知，頻率檢測要求系統運行在混沌態。通常來說被測微弱信號的幅值較小，大多處于0

2.2 方法對比

基于Lorenz混沌同步系統的未知頻率檢測方法與現有的混沌類檢測方法在檢測原理和實現方法上并不相同。分析新方法與現有混沌類檢測方法在構建模型、測量范圍、檢測參數、檢測效率四個方面的區別，其結果如表1所示。

其中，方法1是基于單一Duffing振子，檢測被測信號的幅值；方法2和3采用多個Duffing振子組成陣列，分別基于間歇混沌現象和優化算法匹配被測信號的頻率；方法4基于Chua電路和自適應控制算法檢測信號的頻率；新方法基于Lorenz系統和MUSIC算法獲取信號頻率。

根據上述方法的檢測機理可知，方法1,2,3是需要將系統設定在Duffing振子狀態轉換的臨界點，并通過狀態轉換情況進行判定。若輸入信號疊加Duffing振子系統內原有策動力后所產生信號的幅值超過系統狀態轉換的下一臨界點，將無法引發系統運行狀態改變，從而引發誤判。因此，輸入信號的幅值大小不能超過兩個臨界點之間的區間長度。當使用方法1,2,3中Duffing振子的結構參數時，輸入信號的有效幅值輸入區間為[0,0.5]。方法4基于Chua電路，進行檢測時要求信后輸入前后系統能穩定運行在混沌態，避免進入周期態和發散態。當Chua電路采用方法4中結構參數時，輸入信號的有效幅值區間為[0,0.014]。根據上文的研究可知，新方法基于Lorenz系統構建，輸入信號的幅值在區間[0,45]內時，均可以實現信號檢測。因此，對比上述方法的可測量幅值區間可以得出：S?S1=S2=S3?S4。

方法1無法測量信號的頻率值，方法2和方法3的頻率檢測范圍理論上可以通過增加振子個數或動態調整策動力參數的方式來滿足任意頻率區間的檢測需求。但增加振子個數會使系統結構更加復雜，大大增加系統成本。在相同構建成本的約束條件下有：F≈F4?F3≈F2?F1。

方法2需要按照掃頻方式逐步匹配的頻率值，方法3則需要不斷迭代求解信號頻率，這都會大大增加檢測時間，進而影響檢測效率。根據相關實驗有：T≈T4?T1?T3?T2。

由此可見，基于Lorenz系統構建的混沌同步系統與現有混沌類檢測方法相比，在有效幅值、頻率檢測區間和檢測效率上均具有優勢。

3 實驗驗證

為了對上述方法的有效性進一步進行檢驗，采用電容、電阻、運算放大器(LM741)和模擬乘法器(AD633)，搭建實際Lorenz系統混沌同步檢測電路，如圖7所示。

圖中左側電路為同步電路的驅動端，右側電路為響應端。運算放大器和模擬乘法器的供電電壓分別為±18 V和±10 V。列出驅動端電路的狀態方程有

(10)

式中，A，B，C處的電壓值VA，VB，VC與Lorenz系統的狀態變量xd，yd，zd相對應。r(t)為輸入的被測信號，由正弦信號和白噪聲疊加而成。參照上文仿真的Lorenz系統參數值，C1=C2=C3=0.1 μf，R1，R2，R3，R4，R6，R7，R8，R10，R11，R12，R14為10 kΩ，R5=2 kΩ，R9=100 kΩ，R13=38 kΩ。而響應端電路的狀態方程與上式類似，所用元件的參數值與驅動端同一位置處的元件保持一致。此時同步電路的狀態方程與上文Lorenz同步系統的狀態方程(3)和(4)完全一致。

圖7 Lorenz系統混沌同步檢測電路圖

采用信號發生器疊加幅值為0.001，頻率為30 Hz的正弦信號和白噪聲接入該電路，同時記錄上述各點處的電壓值，采樣率取100 kHz，記錄時長為0.2 s。繪制系統的相空間軌跡圖和同步誤差空間譜，如圖8所示。

上圖可見，所設計的Lorenz同步檢測電路運行在混沌態，計算接入被測信號后同步誤差的空間譜，通過峰值可以觀察到此時被測信號的頻率值為30 Hz，與實際輸入的被測信號完全一致。

4 結 論

本文提出了一種基于混沌同步系統測量強噪聲背景下微弱信號頻率值的新方法，采用Lorenz系統構建了相應的檢測模型，研究了系統的檢測機理、參數設定準則和有效檢測范圍，對比分析了新方法與現有混沌類檢測方法在模型結構、可測量參數和檢測效率等方面的區別，并搭建檢測電路進行了實驗驗證。新方法利用了混沌系統的可同步性，采用MUSIC算法直接從同步誤差獲取待測信號的頻率值，在保留混沌系統優良檢測特性的同時，解決了現有方法參數設定復雜和系統運行狀態判定困難的問題，大大提升了檢測效率和適用性，有利于應用于實際工程，還可與傳統時頻域信號處理方法進行結合，形成新的微弱信號檢測方法，為檢測低信噪比條件下的微弱信號提供新的途徑。