疏水硅膠顆粒的吸能機理研究

趙 鵬， 余慕春， 陳 前

(1. 南京航空航天大學 機械結構力學及控制國家重點實驗室， 南京 210016；2. 中國運載火箭技術研究院， 北京 100076)

沖擊問題廣泛存在于工程實際中，車輛碰撞、飛機降落、載人衛星返回艙的著陸都伴隨著沖擊的發生[1-3]。為了確保更高程度的個人和公共保護，對吸能結構的設計和應用提出了越來越多的要求。從20世紀70年代開始，用于耗散碰撞動能吸能材料的研究和開發成為工程領域的熱點，已廣泛用于車輛防護、工業事故防護和個人防護中。

近年來，研究發現微孔功能材料具有獨特的力學特性。根據水進出疏水微孔是否產生遲滯現象，可以將這種液固介質分為無阻尼的分子彈簧[4-7]和有阻尼的疏水硅膠[8-11]。Fadeev等首先通過試驗發現，當載荷加載至特定的壓力時，水分子開始大量侵入疏水硅膠的納米微孔中，吸收儲存機械能；在卸載階段，水分子逸出納米微孔較為困難，在逸出微孔的同時會產生顯著的遲滯現象并消耗大量的能量。并且研究了疏水硅膠的硅烷鏈長度，覆蓋密度、硅烷鏈結構、硅膠孔徑等因素對水分子進出疏水微孔壓強的影響。Suciu等和Lefevre等分別對疏水顆粒產生遲滯現象的原因進行了闡釋。Suciu等認為疏水硅膠產生遲滯是因為微孔液-固界面接觸角的滯后；Lefevre等根據能壘計算了水逸出微孔的臨界壓強和孔徑的關系，得出隨微孔孔徑減小，水逸出疏水微孔的壓強顯著增加的結論。目前，針對疏水硅膠緩沖介質的研究主要關注其微觀工作機理，對于宏觀力學建模的研究和緩沖應用還有待于進一步開展。本文將結合微觀工作和材料物理特性的統計規律進行宏觀力學建模，并進一步分析材料的吸能特性和緩沖效率。

將疏水硅膠緩沖介質封存于如圖1所示的活塞液壓缸結構中，即可形成疏水硅膠緩沖器。沖擊發生時，水分子進出硅膠顆粒的疏水微孔，從而實現能量的消耗。本文基于理論分析和試驗測試，建立了并驗證疏水硅膠顆粒的宏觀力學模型。首先，基于Laplace-Washburn方程和接觸角遲滯模型，揭示水進出疏水微孔產生遲滯現象的機理，建立疏水硅膠力學性能的理論計算模型；隨后，以C-18疏水硅膠與水的混合物為工作介質，開展試驗測試其準靜態特性，通過對比試驗測試結果和理論分析結果驗證本文理論方法的準確性。最后，本文分析沖擊載荷作用下疏水硅膠緩沖器的耗能特性。本文研究內容將為疏水硅膠緩沖介質的工程應用奠定良好的基礎。

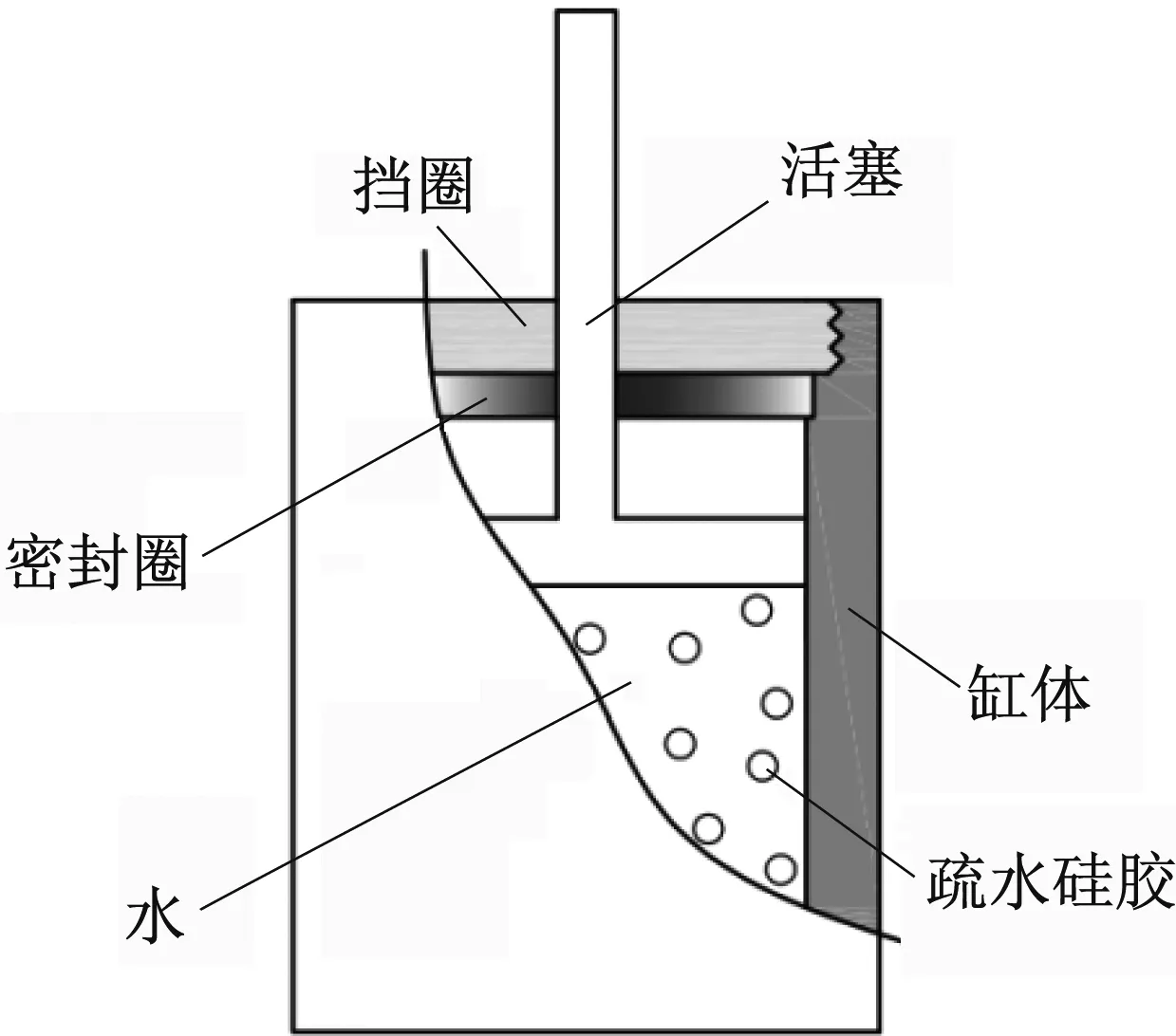
圖1 疏水硅膠緩沖器示意圖

1 力學模型建立

目前，對于疏水硅膠特性研究主要集中于試驗測試，較少涉及疏水硅膠的力學行為的力學模型。本節以疏水微孔內的液柱的微觀力學行為基礎，建立水進入和逸出單條疏水微孔的微觀力學模型，并結合材料物理特性的統計規律，實現疏水硅膠的宏觀力學建模。

1.1 疏水微孔液柱微觀力學行為

對于疏水微孔液固接觸界面，其接觸角θ大于90°。水進入單條微孔時的受力情況如圖2所示。其中Pc是附加毛細力，Pair是孔內氣體壓強，P是外部液體壓強。微孔內水受力平衡如式(1)所示

P=Pc+Pair

(1)

毛細孔內液固界面接觸的Laplace-Washburn方程為

Pc=-2σLcosθ/r+Pair

(2)

式中：σL為液體表面張力，r為微孔半徑，θ為接觸角。

圖2 水侵入單條疏水微孔受力圖

對于納米級高疏水性微孔，可忽略Pair[12]。在此基礎上可以得到水侵入單條疏水微孔所需的外部壓強P為

P=Pc=-2σLcosθ/r

(3)

由式(3)可知：可以通過微孔的物理參數計算水進入微孔所需的壓強P，而不考慮整個入水的過程，因此能夠較為方便準確的計算出這一特定外加壓強。

水逸出疏水微孔的過程可以看作是侵入微孔的逆過程，同樣遵循Laplace-Washburn方程，但在卸載階段，疏水硅膠的體積變化量比加載階段要小，即產生了遲滯現象。文獻[13]表明，正是由于水進入和逸出疏水微孔的接觸角存在差異，才導致加載卸載過程存在遲滯現象。接觸角遲滯產生的原因為液-固接觸界面粗糙引起的[14-16]，液-固接觸界面的粗糙包括物理粗糙(接觸界面不光滑)和化學粗糙(接觸界面化學性質不均勻)引起的。納米尺度下水侵入和逸出疏水微孔的遲滯現象如圖3所示。當水侵入單條疏水微孔時，其接觸角為θa；水逸出同一微孔時，其接觸角變為θr，并且有θa>θr。由式(3)可知，當水進出微孔的接觸角不同時，入水壓強要大于出水壓強，即在加載卸載過程產生遲滯現象。

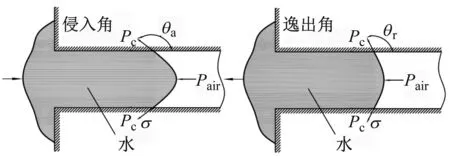
圖3 接觸角遲滯模型

1.2 疏水硅膠宏觀力學建模

當壓縮疏水硅膠緩沖器時，水分子開始侵入大量疏水微孔，由于這些微孔的孔徑及疏水性不盡相同，因此需要結合材料物理特性的統計規律進行宏觀力學建模。疏水硅膠在加載階段體積變化量與外加壓強之間的關系分為三個階段：第一階段和第三階段斜率相同，第一階段，外壓力不足以迫使水分子進入硅膠顆粒的疏水微孔，隨著壓力的增加，液體的可壓縮性使得疏水硅膠體積減小；與第一階段不同的是，在第三階段，微孔已經完全達到飽和，水分子無法進入微孔，同樣是液體的可壓縮性使得疏水硅膠體積持續減小；第二階段，外界壓強達到水分子進入微孔的臨界壓強，開始迫使水分子大量進入硅膠顆粒的疏水微孔，此后，較小的壓力增加將引起疏水硅膠的體積大幅度減小。因此在水侵入大量疏水微孔的過程中，可以觀察到明顯的分段特性。

設外加壓強為P，疏水硅膠的總體積變化量V(P)；疏水硅膠孔徑最大值為rmax，孔徑最小值為rmin；入水階段，疏水硅膠顆粒接觸角最大值為θmax，最小值為θmin；疏水硅膠質量為m；單位質量疏水硅膠顆粒有效孔容積為Vp；水的體積為Vw；K(P)為水的壓縮率；V(r)為有效孔容積相對于孔徑的概率密度函數，f1(θ)為接觸角的概率密度函數。則有：

K(P)=4.5×10-4(P×10-6-0.1)

(4)

(5)

(6)

其中：

(7)

(8)

由式(6)和(7)可知，f(θ)是高斯分布的概率密度函數；F(θ)是高斯分布的概率分布函數。

第一階段和第三階段疏水硅膠的體積變化量可以通過水的壓縮率來計算，當外加壓強從峰值開始逐漸增大時，由于液體的可壓縮性，疏水硅膠的體積變化量為

V(P)=VwK(P)

(9)

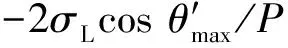
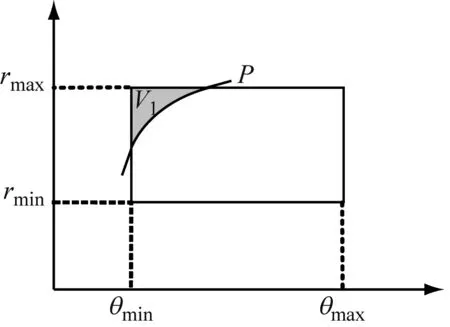
(a) 入水第一階段

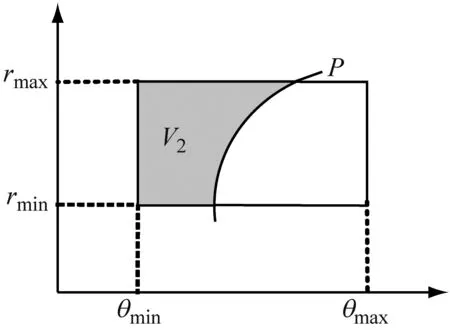
(b) 入水第二階段

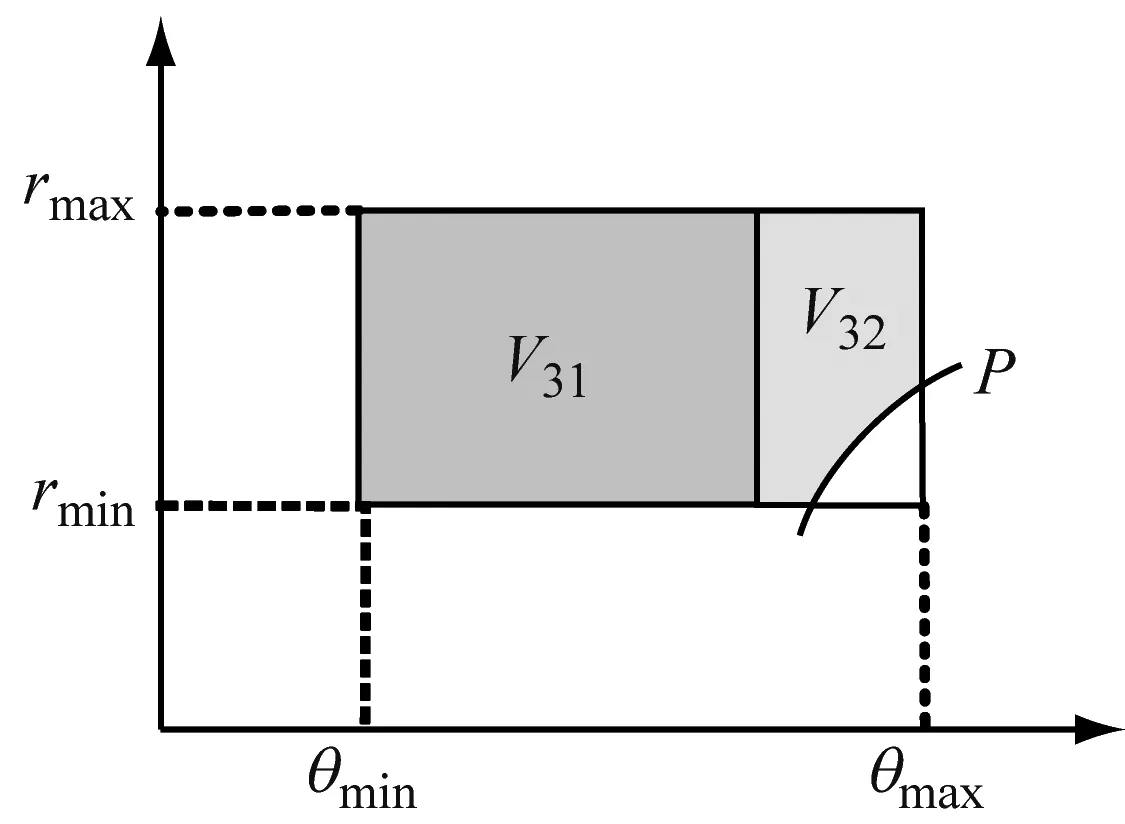
(c) 入水第三階段

結合圖4，逸出微孔水的體積為

V1(P)=VwK(P)+

(10)

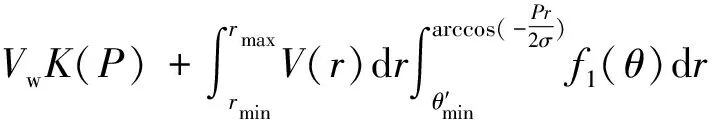
(11)

V3(P)=V31(P)+V32(P)

(12)

其中：

(13)

(14)

當外加壓強逐漸增加到臨界壓強時，水已經完全侵入疏水微孔，由于液體的可壓縮性，疏水硅膠的體積的變化量為

V(P)=VwK(P)+mVp

(15)

綜合式(9)～式(15)，以Laplace-Washburn方程為基礎，結合接觸角遲滯模型，可以得到疏水硅膠在加載階段體積變化量與外加壓強之間的關系。其中，式(9)和式(15)分別表示純水壓縮過程中的體積改變量，式(10)～式(14)表示第二階段水分子侵入疏水微孔過程的體積改變量。

水逸出疏水微孔的過程是進入疏水過程的逆過程，由于接觸角遲滯，水逸出疏水微孔的臨界壓強遠低于水進入疏水微孔的臨界壓強。從而使得在相同的壓強下，卸載階段疏水硅膠的體積變化量比加載階段要小。基于上述假設，認為水逸出大量微孔時的接觸角分布和侵入微孔時一致，同樣服從正態分布θ～N(μ,η2)，只是卸載階段疏水孔道的接觸角分布值小于加載階段的接觸角。這一假設采用統計的方法，綜合考慮硅膠微孔表面粗糙度和化學性質差異性，得到的結果更符合實際情況。水逸出疏水微孔的過程與侵入微孔的過程類似，在這里就不在贅述。

將表1中的仿真參數代入式(9)～式(15)中，其中，室溫下水的表面張力為0.072 8 Pa，正態分布參數根據材料自身規律確定，其余材料參數由材料生產廠家提供。采用數值積分的方法，處理并化簡后可得疏水硅膠在加載-卸載階段體積變化量和外加壓強的關系如圖5所示。由圖5可知，在15 MPa水分子開始進入疏水微孔，47 MPa飽和，2 MPa逸出，-5 MPa排凈。實際應用中，由于液壓缸體內無法產生負壓強，會有部分水分子滯留在疏水微孔中，無法逸出。

表1 仿真參數

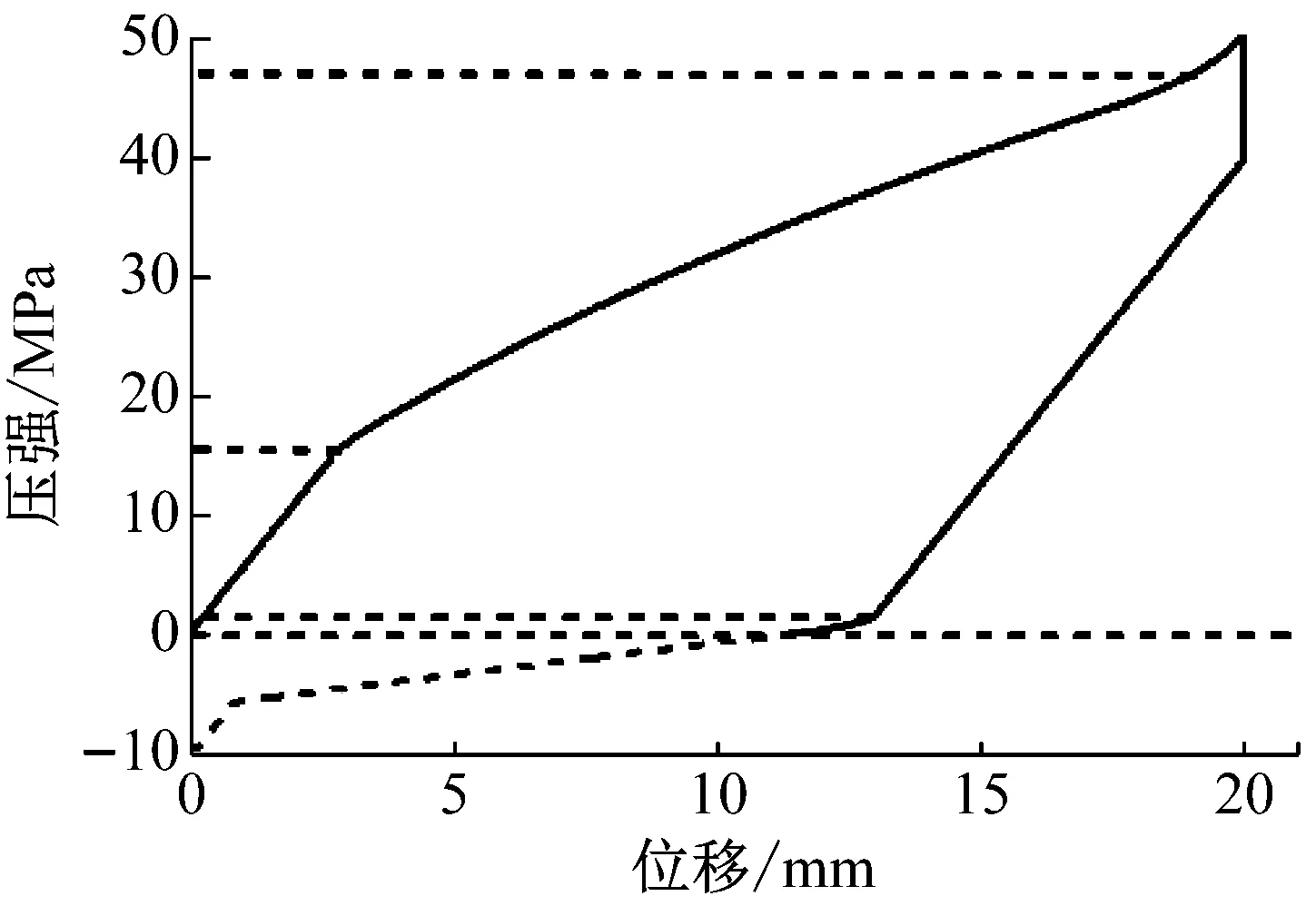
圖5 疏水硅膠理論結果

2 試驗驗證

為驗證本文疏水硅膠理論模型的準確性，本文設計一種疏水硅膠緩沖器，并通過疲勞試驗機對疏水硅膠緩沖器進行加載—卸載，得到準靜態條件下，緩沖器的力-位移曲線。試驗裝置如圖6所示，將一定量的水和C-18疏水硅膠組成的混合介質置于密封的活塞液壓缸中，形成疏水硅膠緩沖器；圖7為該裝置所用的C-18疏水硅膠。其中C-18疏水硅膠的平均粒徑和孔徑分別為50 nm和6 nm，液壓缸活塞直徑和缸體體積分別為10 mm和30 mL。

圖8給出了疏水硅膠的準靜態實驗結果。從圖8可以看出，在加載階段，疏水硅膠表現出明顯的分段剛度特性。第一階段和第三階段的斜率幾乎相同，說明這兩個階段的主要過程為水的壓縮過程，沒有水分子進入疏水微孔。第二階段斜率降低是由于在該階段，水分子開始大量侵入疏水微孔；卸載階段是加載階段的逆過程，但在卸載階段，疏水硅膠的體積變化量要遠遠小于加載階段，侵入微孔的水并沒有完全逸出疏水微孔，產生較大的遲滯現象。利用接觸角遲滯理論可以解釋遲滯現象產生的原因。當入水接觸角與出水接觸角相差較大時，雖然入水時的接觸角大于90°，但出水時的接觸角有可能接近90°，甚至小于90°。因此，在卸載過程中，對于一些接觸角小于90°的微孔，水將滯留在微孔中。只有接觸角大于90°的疏水微孔中的水能夠逸出微孔。此外，由于疏水微孔表面的某些缺陷，也會使得部分水分子被滯留在微孔中，從而導致遲滯現象的發生。在開始卸載過程中力信號出現一定程度的衰減，該現象出現的原因可能是由于試驗機存在一定的機械間隙，導致在卸載階段，施加的作用力未能補償該間隙。

圖6 試驗裝置

圖7 疏水硅膠顆粒

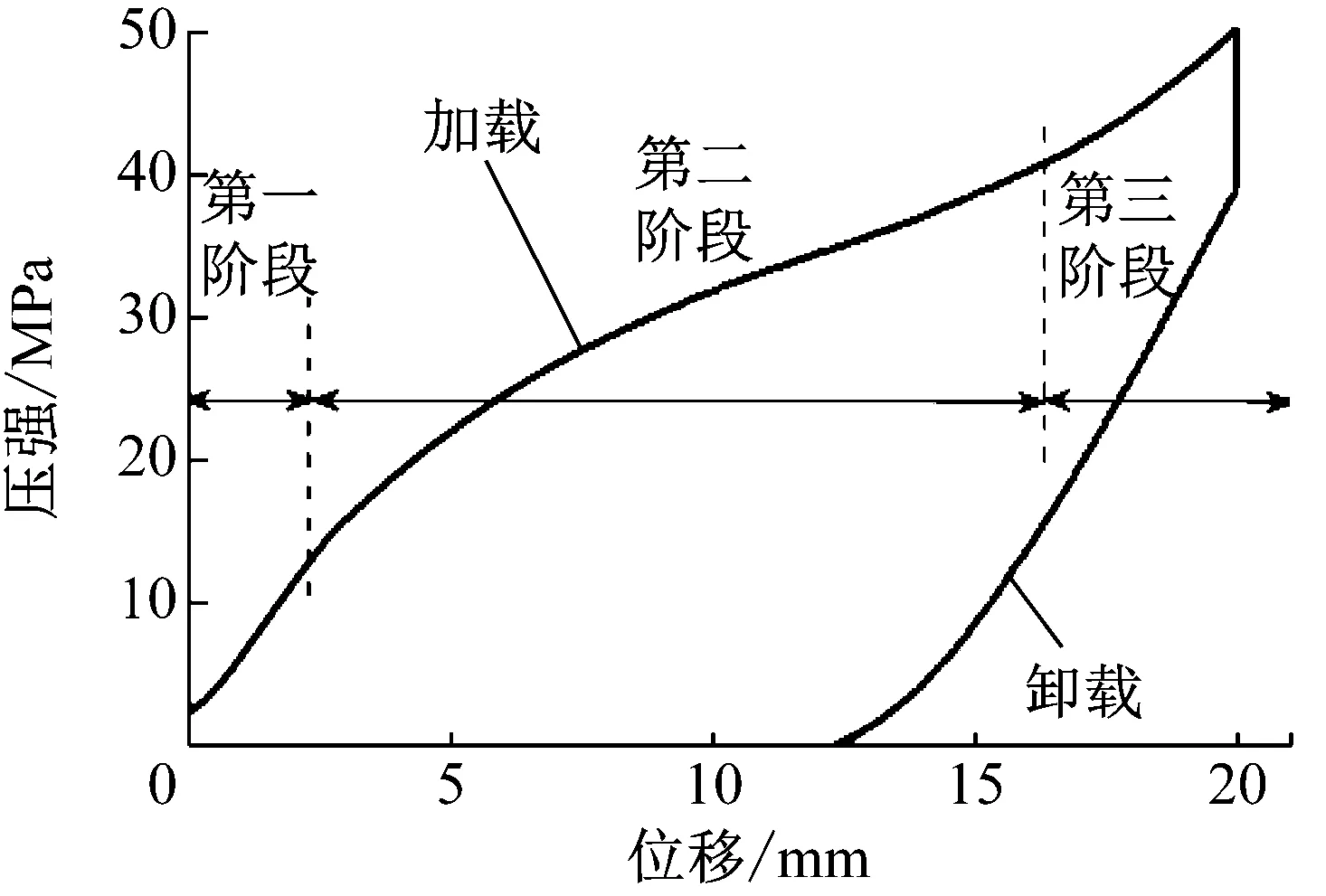
圖8 準靜態試驗結果

為了進一步驗證上述理論，圖9給出了在多次循環載荷下，疏水硅膠的加載-卸載曲線。從圖9中可以看出，疏水硅膠的遲滯環面積隨著循環次數的增加而減小。在第一次循環時，可以看到明顯的遲滯現象，此時耗能效果最為顯著。隨著循環次數的遞增，耗能效果會逐步減弱。后三次循環的遲滯效果雖然十分接近，但與第一次相比，仍然有較大差距。進一步說明由于接觸角的差異，導致部分水分子無法逸出微孔，從而削減了疏水硅膠后續耗能效果。

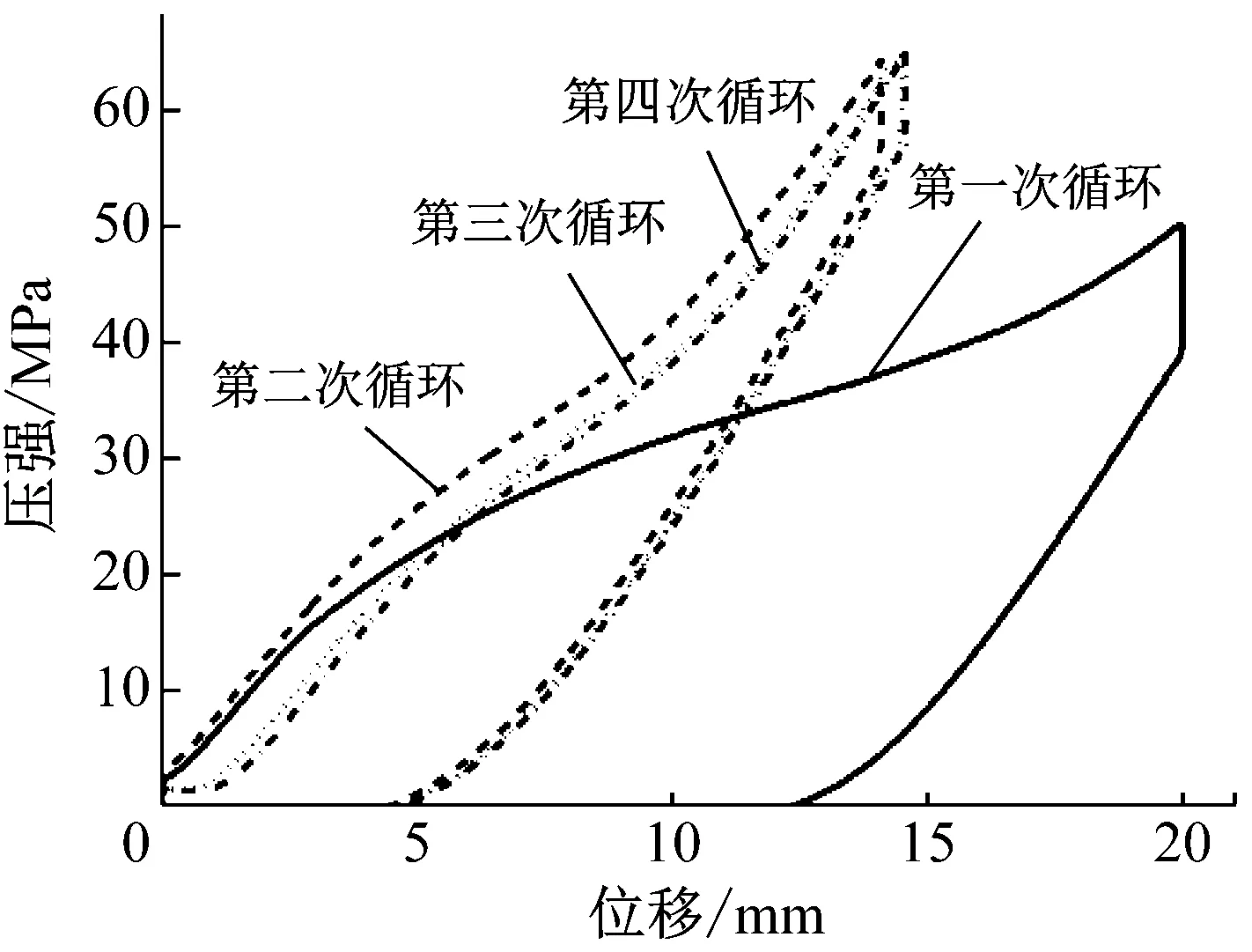
圖9 多次循環載荷下的遲滯效應

圖10是將理論結果和第一次循環載荷下的試驗結果相比較。由圖可知，在加載階段，二者吻合的較好。在卸載階段，部分理論計算結果和試驗結果出現了一定的偏差，這是因為在加載階段，水分子侵入疏水微孔，導致缸體內純水體積減少，使得在卸載階段，純水的體積變化量較理論值有一定偏差。值得說明的是，在卸載階段，由于力信號出現衰減和部分微孔接觸角變小，使得當缸體內壓強達到零時，仍有部分水分子滯留在微孔中。如圖10所示，利用理論模型可以計算出外部壓強小于零時水逸出疏水硅膠的過程，驗證了疏水硅膠的工作機理。

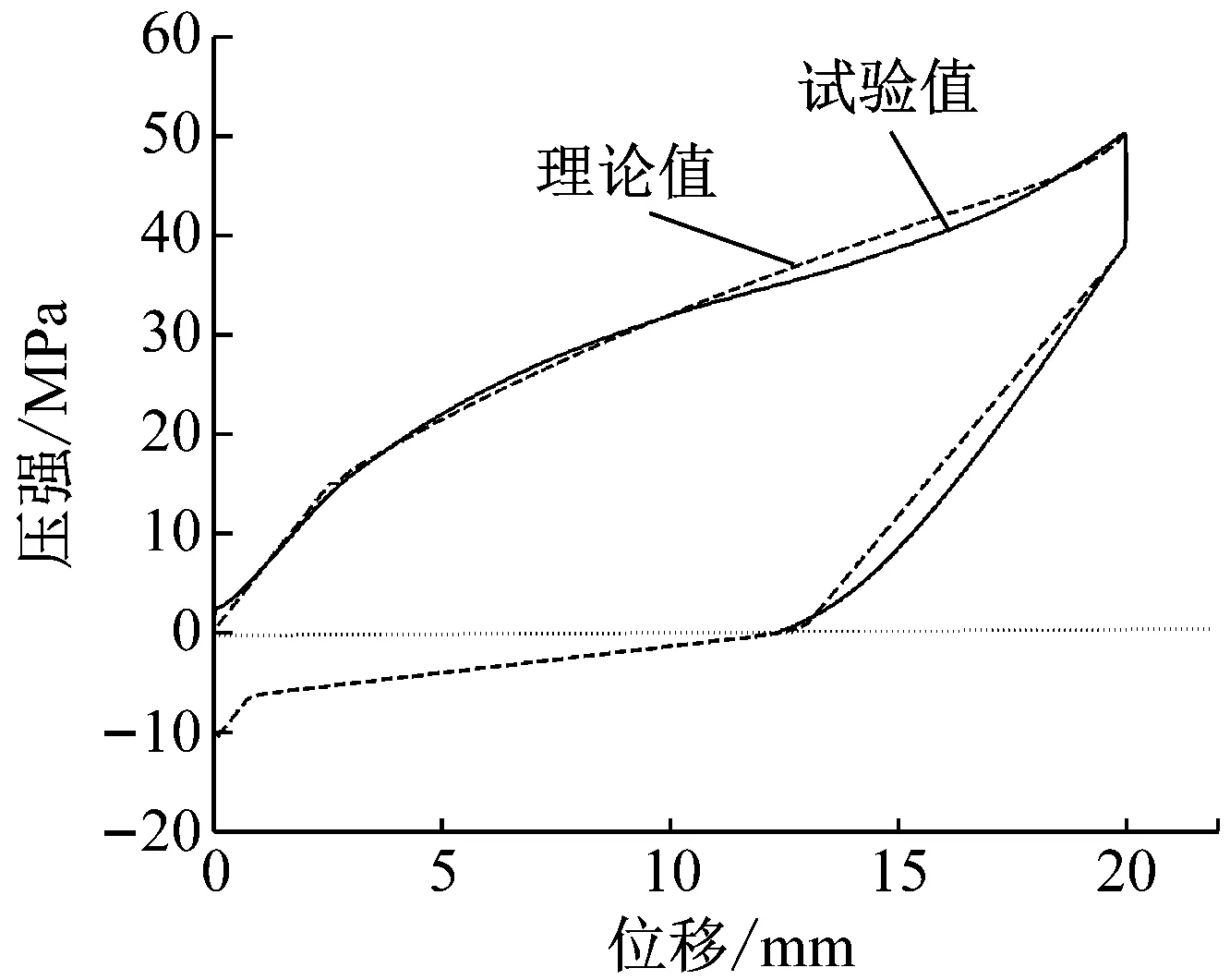
圖10 第一次循環載荷時試驗結果與理論結果比較

為了進一步驗證理論結果的正確性，將理論結果和第二次循環載荷下的試驗結果相比較。由于部分水分子滯留在疏水微孔中，在第一次循環載荷結束后，認為單位質量疏水硅膠顆粒有效孔容積將有所減小，其余物理量保持不變。試驗表明：單位質量疏水硅膠有效孔容積由原來的1.70-7m3降為4.58×10-8m3，將改變后的有效孔容積和表1中的其他參數代入式(9)式(15)中，可得疏水硅膠在第二次循環載荷下，體積變化量和外加壓強的關系，理論與試驗對比結果如圖11所示，由圖11可知，理論計算結果和試驗結果吻合較好，同時也說明了當部分水分子滯留微孔時，僅會改變疏水硅膠的有效孔容積，并不會對其他物理量產生影響。

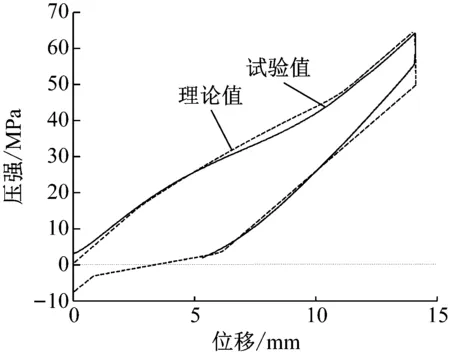
圖11 第二次循環載荷時試驗結果與理論結果比較

3 耗能特性分析

本節中對疏水硅膠緩沖器的耗能特性進行分析。一個理想緩沖器應該在降低最大沖擊力峰值的同時吸收更多的能量。因此，在沖擊發生時，緩沖器受到的作用力會急劇增加，并且會在該峰值保持一段時間。沖擊結束后，緩沖器受到的作用力急劇下降，發生遲滯現象，從而吸收消耗能量。

圖12是疏水硅膠緩沖器第一次循環時的加載—卸載曲線。在圖12中，曲線A-B-C-D和曲線D-E-F分別為加載曲線和卸載曲線。加載曲線A-B-C-D和卸載曲線D-E-F所圍成的面積代表疏水硅膠消耗的能量Ed，加載曲線A-B-C-D與x軸所圍成的面積代表一個循環載荷下，疏水硅膠吸收的總能量Ea。緩沖器的緩沖效率(表征消耗能量的能力)η定義為

(16)

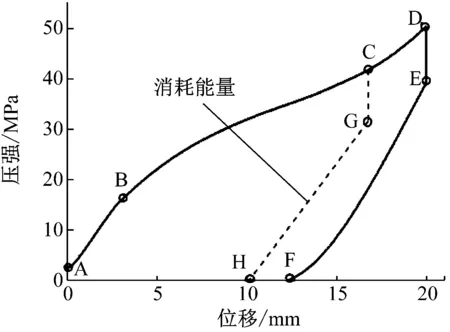
圖12 疏水硅膠耗能特性

利用圖12的實測數據可以計算出疏水硅膠緩沖器在一個循環載荷下的緩沖效率為79.3%。相比之下，液壓緩沖器的緩沖效率通常低于50%，而在實際應用中，其效率往往只能達到30%～40%。計算結果表明疏水硅膠緩沖器具有優異的耗能特性。

為了降低緩沖過程中最大沖擊力幅值，疏水硅膠緩沖器的最大位移值應限制在疏水硅膠的入水階段，一旦緩沖器位移進入第三階段，沖擊力幅值會大幅度增加。換言之，最大位移應限制在B-C之間，如圖12所示。加載-卸載曲線應為A-B-C-G-H，此時非常接近理想緩沖器的遲滯曲線。在該情況下，沖擊力幅值將得到有效抑制。此時，計算得到疏水硅膠耗散的能量為327.53 J。考慮到緩沖器中填充5 g硅膠顆粒，因此每克硅膠顆粒能夠吸收65.5 J的機械能。此外，可以通過改變填充疏水硅膠的質量從而改變疏水硅膠緩沖器的緩沖特性，以滿足不同的緩沖要求。

除了具有良好的耗能特性，疏水硅膠緩沖器還具有諸多優點：疏水硅膠緩沖器與液壓式緩沖器不同，液壓式緩沖器通過熱能耗散的方式消耗機械能，而疏水硅膠緩沖器則是利用水進出疏水微孔，通過產生更多的液固界面，將機械能轉化為液-固表面的界面能。因此，疏水硅膠緩沖器在緩沖過程中產生的熱量十分有限。此外，疏水硅膠是將烷基氯硅烷嫁接到傳統硅膠顆粒而形成的有機物。由于烷基氯硅烷鏈長的不同，可以合成出具有不同孔道結構和拓撲形狀的疏水硅膠顆粒，從而滿足不同的緩沖要求。

4 結 論

本文發現了一種新型緩沖材料——疏水硅膠顆粒，從Laplace-Washburn方程和接觸角遲滯模型出發，討論了疏水硅膠顆粒產生遲滯現象的原因，并建立了理論計算模型，該模型的仿真結果與準靜態試驗結果有吻合較好；本文對疏水硅膠力學性能進行了理論研究和試驗，發現在初次載荷下，疏水硅膠顆粒具有優異的吸能效果；在后續載荷中，耗能特性雖有所下降，但仍有持續的耗能效果，特別適合于航天器回收、飛機起落架、車輛懸架防護等領域。本文主要結論歸納如下：

(1) 準靜態條件下的試驗結果和理論結果具有較好的一致性，這表明了本文理論方法的合理性和有效性。

(2) 在多次循環載荷下，疏水硅膠的遲滯效應會隨著循環次數的增加而減小，導致在后續的緩沖過程中，疏水硅膠的耗能效率有一定程度的減少。

(3) 疏水硅膠具有優異的緩沖特性，在第一次循環載荷下，其緩沖效率為79.3%，遠遠優于液壓緩沖器的緩沖性能。