不一樣的冒泡排序

陳凱

冒泡排序是一種著名的排序算法，雖然效率不高，但這種排序方法有著它自身的獨特性：它和大部分人類習慣的排序方法不同，但對于機器來說，卻反而是比較容易實現的。初次遇見冒泡排序的學習者，往往會被循環嵌套的代碼弄暈。本文從幾個簡單的小游戲入手，由簡入難，逐步展現出使得數據排序得以自動進行的關鍵思路。

上升的氣球與受限的工作空間

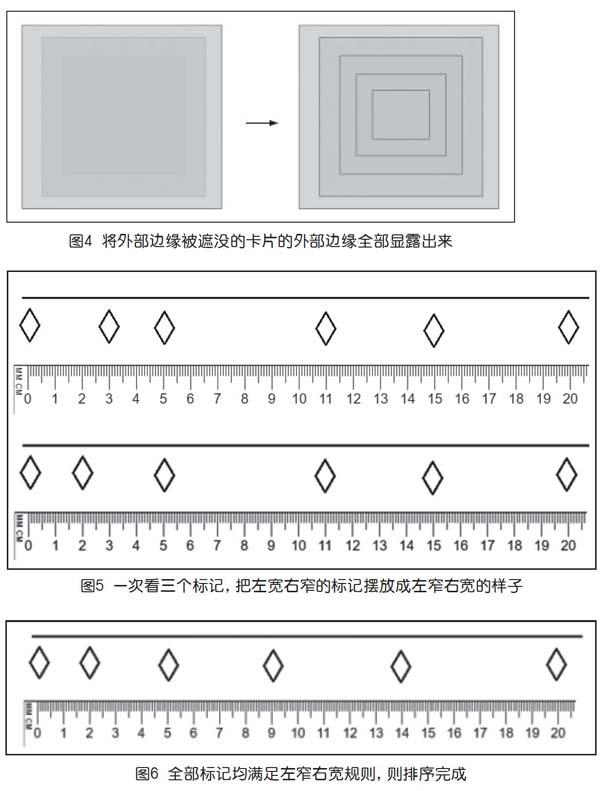
Algodoo是一個仿真物理沙盒軟件，用這個軟件可以輕松地創造出排序任務情境。例如，給出若干個密度不一樣的氣球，按它們的上升速度進行排序，如圖1所示。在Algodoo場景中，可以看出氣球都被放置在一個矩形盒子中，以免飄走，而測試氣球的豎立軌道每次只能容納兩個氣球進行測試。這樣設計場景的意圖是，其一，無法直接看出被比較物體的大小順序，必須測試后獲得結果；其二，測試軌道空間有限，用來比喻冒泡排序所需要的不大的存儲空間。

在這個氣球測試場景中，雖然氣球上升測試窗口受限，但氣球選擇的順序卻是不受限制的，所以可以進一步優化場景，使得其和冒泡排序程序實現過程更加相像。比如，可以制作一個帶狹縫的擋板，抬起擋板后側的欄桿，就可以在狹縫中觀察氣球的上升速度，然后根據上升速度重新調整氣球位置，如圖2所示。不過因為狹縫空間小，每次只能交換相鄰氣球的位置，可以將那個狹縫看作是機器在進行冒泡排序時的“視角”和“工作空間”，用以印證冒泡排序所需要的很低的空間復雜度。

堆疊的卡片與流程化的比較交換過程

對若干數量并不多的數據排序時，人眼往往很快就能找出其中的最大值或最小值，但機器是不會自動擁有這種直觀能力的，所以在學習冒泡排序時，就先要假裝自己看不出誰大誰小，這種“假裝不知道”的操作會對初學者產生一定困擾，不妨設法讓學習者從假裝不知道，變成真的不知道，還原出機器所面臨的問題。

例如，有這么一個任務，在演示文稿中，有五張不同大小的卡片堆疊在一起（如上頁圖3），要求對卡片只能使用“下移一層”和“置于底層”操作，并且只能對最上面的一張卡片進行操作，任務目標是將卡片的排列方式變化為從右下到左上角層層堆疊。為了能夠看出卡片相互之間的關系，每張卡片是半透明的，即便如此，當卡片比較多，堆疊又隨機亂序的情況下，若想要快速完成任務，并沒有想象中那樣簡單，不僅需要眼力和耐性，還要一些小小的訣竅。

卡片稍微多一些，操作者難免會眼花目眩，可以借用冒泡排序的思路，讓排序過程變得“傻瓜化”。以五張卡片為例，每次只比較最上面一張和最上面第二張的卡片次序是否正確，如不正確，則將第一張卡片“下移一層”，然后將剩下的最上面的卡片“置于底層”；如次序正確，則只要將當前最上面的卡片“置于底層”即可。假如有五張卡片，那么先比較四次，然后無條件執行一次“置于底層”，接下來，再比較三次，然后無條件執行兩次“置于底層”，接著，比較兩次，無條件執行三次“置于底層”，最后再比較一次即可完成排序任務。這恰好就對應著冒泡排序的比較過程，對于n個數據冒泡排序，第1輪需要比較n-1次，第2輪需要比較n-2次，直到第n-1輪只要比較1次。

這里有一項更困難些的任務，若卡片形狀相同，面積不同，要求將堆疊在一起的所有卡片的外部邊緣顯露出來，規則仍然是只能對最上面的卡片進行操作，并且只能執行“置于底層”和“下移一層”操作，如圖4所示。當卡片比較多的時候，只憑眼力和記憶完成任務，是頗有困難的，但若借用冒泡排序的方法，按流程機械性地進行比較和交換，雖然耗時比較長，但肯定可以完成任務。

滑動的標尺與數學模型

以上幾個游戲都實際體驗過之后，再回頭來看冒泡程序的代碼，是不是感覺代碼變得簡單了呢？接下來不準備介紹大家都已經非常熟悉的傳統的冒泡排序程序代碼，而是試著來完成一段有點小小奇葩的代碼：既用不到傳統冒泡排序代碼中的嵌套循環，也不用兩兩比較數據大小，卻能完成冒泡排序。

一般來說，冒泡排序需要一個一維的數組空間，可以用一個一行n列的表格及若干數字來演示比較和排序過程。但若用一把尺子和若干標記，也是可以實現冒泡排序的。

假設等待完成排序的數字是[3，2，6，4，5]，在尺子0厘米和3厘米處標記號，兩個記號之間的距離正是3，代表等待排序的第一個數據；接著在5厘米處標記號，5厘米處記號與3厘米處記號距離是2，代表等待排序的第二個數據……以此類推，于是在尺子的0厘米、3厘米、5厘米、11厘米、15厘米、20厘米處共標了6個記號。相鄰記號之間的距離就代表了等待排序的數字。接下來，一次看三個標記，把左寬右窄的標記擺放成左窄右寬的樣子即可，如上頁圖5所示。當全部標記均滿足左窄右寬規則時，排序就完成了，如上頁圖6所示。

這種方法在程序實現中，乍看上去似乎都不需要做比較大小的判斷，筆者給出的程序代碼中，借用了一個絕對值函數，就實現了將左寬右窄的標記擺放成左窄右寬的功能。并且，代碼前半段直接生成了等待移動的標記序號，所以也用不到在循環結構中嵌套循環結構。等待排序的數字是[6，5，4，3，2]，對應到尺子上的標記，就是0厘米、6厘米、11厘米、15厘米、18厘米、20厘米這6個標記。所生成等待移動的標記序號就是[1，2，3，4，1，2，3，1，2，1]，很顯然，0厘米位置的標記和20厘米位置的標記不需要移動，因為第一輪最多需要移動4次標記，第二輪最多移動3次標記，第三輪最多移動2次標記，第四輪最多移動1次標記，總共是移動10次標記。當標記很多的時候，可以利用數學公式“首項加末項乘項數除以二”來得到所需要的最多移動次數。程序代碼和運行結果如圖7所示。

這樣，就實現了一個既沒有大小比較，又沒有循環嵌套結構的冒泡排序程序代碼。希望學習者能通過這個例子，感受到數學模型和數學方法對于解決某特定信息技術任務的重要作用。